【数学興味】「コラッツの問題」に素人が怖いもの知らずで切り口を入れてみた件３

前回のＮＯＴＥ

前回の続きのＮＯＴＥです。

１．操作②による偶数の出現

操作②をした時に２の累乗数の違いで偶数を分類してみることにしました。１～１億の間に存在する任意の奇数を５０００個抽出して操作②を行った結果、１つ増えるごとに半減していく傾向が見られました。個数が半減するイメージを面積にしたのが上スライドの右図です。個人的には物理や化学で習う半減期のグラフを思い出しましたね。

半減期 - Wikipedia

２．出現する偶数の割合予想

先ほどの結果を受けて、奇数と偶数が等量存在するとしたら２＾１偶数は奇数の約半数、２＾２偶数～２＾∞偶数の総数も奇数の約半数となる予想を立てました。

３．各偶数の数値の倍率

操作中において、偶数は含まれている２の累乗の数だけ数値を半分にするルールが操作①でした。操作②の＋１が計算に与える影響を無視した場合、操作①⇄操作②１回分で２＾１偶数は数値が３／（２＾１）倍に増加しますが、それ以外の偶数は数値が３／（２＾２）倍以下に減少します。

４．素人の予想

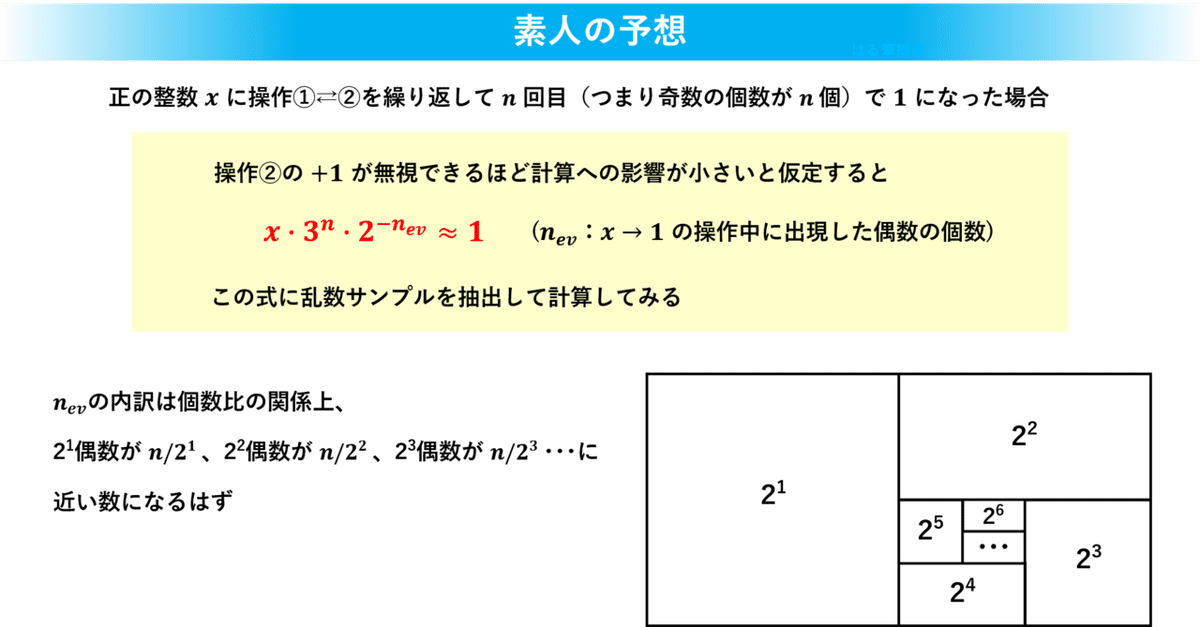
まず、サンプルとなる整数をｘ、操作①⇄操作②を繰り返す回数をｎとします。すると、ｎは奇数の個数と同数となります。偶数の個数はｘ次第で変化するのでｎevと表記すると次式が立てられます。

与式：ｘ・３＾ｎ・２＾（－ｎev）≒１

ちなみにこの式は操作②の＋１が計算に与える影響が無視できるほど小さいときに成立します。さて、１～１０兆までの偶数・奇数サンプルを各８００個抽出して与式で計算してみましょう。

５．計算結果

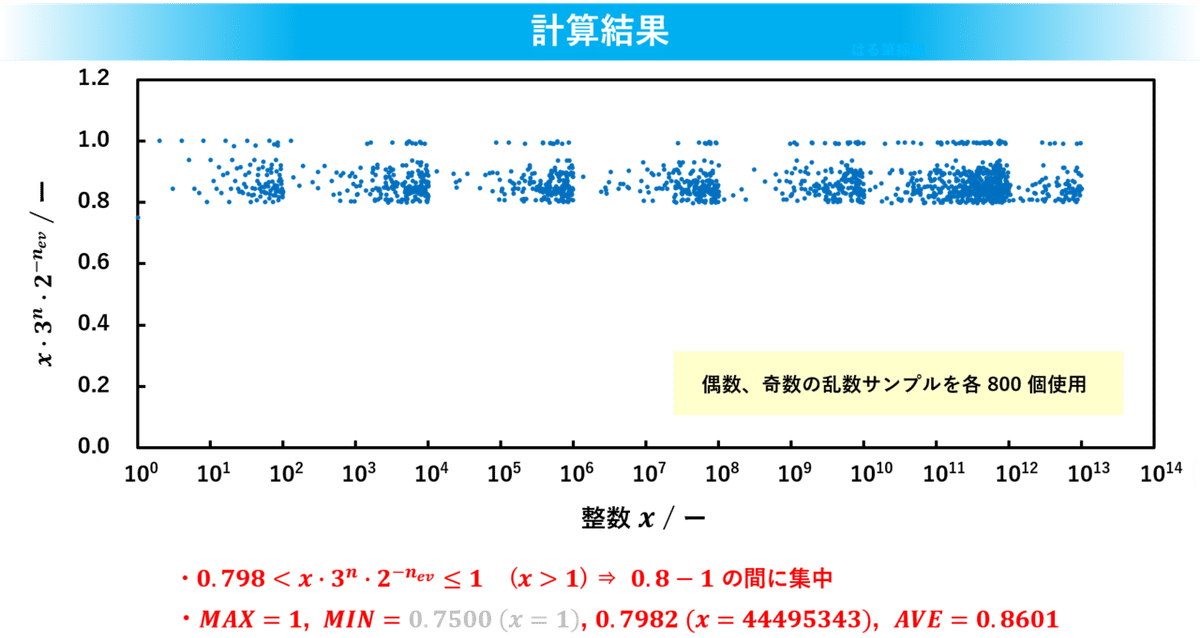
サンプル整数ｘの大小に関わらず与式の計算結果はおよそ０．８から１の間にきれいに揃いました。最大値はｘが２の累乗数になる場合でもちろん１です。最小値はｘ＝44495343の時で０．７９８２でした。ちなみに、ｘ＝１は終了条件ですが、これも含めて計算すると最小値は一気に０．７５にまで下がります。

次は、操作②で＋１をしなかったがために生じた誤差の大きさについて考察をしましょう。以下、興味本位で調べた内容は目次の通りで２００円となります。素人ゆえに数学の程度が低い、間違った見解をしている、想像していた内容と違う等のクレームは一切受け付けません。それでも構わないという方のみ先にお進みくださいませ。