11月23日はフィボナッチ数列と黄金比と音楽と小説と受験を語ろうのお話💖

今日は11月23日です。
そこで、１・１・２・３、の並びにちなんでこんな問題から。

🌻ある規則に従って数を並べました。どんな規則かを考え、この次にくる数字を答えなさい。

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …

正解は…
🍂2つ前の項と1つ前の項を足し合わせて作った数列

ですね。ですから89の次は、89＋55＝144です。

これはイタリアの数学者フィボナッチによって有名になった、
🍂フィボナッチ数列
といわれるものです。
今日の日付、1, 1, 2, 3もフィボナッチ数列になっているのです。

漸化式で一般的に表現するとこうなります。

🍏フィボナッチ数列を図形にしてみると

フィボナッチ数列は、図形で表すこともできます。
🍎1辺の長さが1の正方形を2つならべます。
すると横の長さは1、縦の長さは2になります。
🍎その隣に、1辺の長さが2の正方形をおきます。
横の長さは3になりますが縦の長さは2のままですね。
🍎その下に（上でもよいですが）横の長さ3を一辺とする正方形を描きます。
すると横の長さは３のままで縦の長さは５になります。
フィボナッチ数列と同じ数字が現れていることにお気づきでしょうか。
🍎以下同様に、1辺の長さが5の正方形、8の正方形、13の正方形…を並べていって、大きな長方形を作ります。
こうして作られていく長方形の縦・横の長さを並べると、
フィボナッチ数列になるのです！（下図）

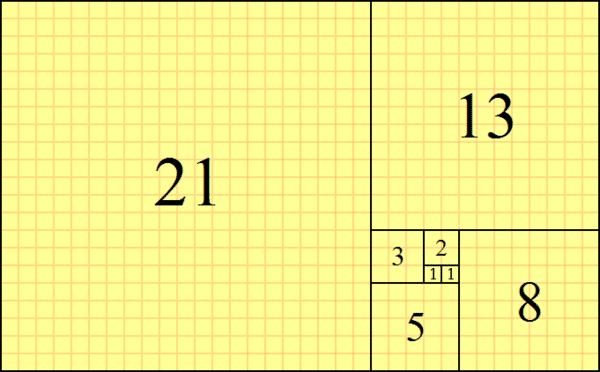
画像は縦21、横34までやったところの長方形です。
実際に一度手を動かしてみるとよく理解できますので、
ぜひやってみてください！

🍏渦巻を描いてみると

自然界において、
どういうわけかフィボナッチ数列がよく出現することが知られています。
例えば、先ほど描いた長方形に渦を描いてみると…

どこかで見たことありませんか？そう、これですね！

アンモナイトやオウムガイの渦巻は、
このようなフィボナッチ数列な形を描くことが知られています。

🍏まだある自然界のフィボナッチな面々

🍁花びらの数はフィボナッチ数であることが多いです。

3枚:ユリ、アヤメ、エンレイソウ
5枚:オダマキ、サクラソウ、キンボウゲ、ノイバラ、ヒエンソウ
8枚:デルフィニウム属、サンギナリア、コスモス
13枚:シネラリア、コーンマリゴールド
21枚:チコリー、オオハンゴンソウ
34枚:オオバコ、シロバナムシヨケギク
55枚:ユウゼンギク
89枚:ミケルマス・デイジー

などなど。
ただし、花びらの数が144に達することはありません。
この89という数は、
他の自然界に見られるフィボナッチ数の例でも限界になっていることが多いらしいです。
特別な数なのでしょうか？

🌻ひまわりの種など、植物の花や実に現れる螺旋の数もフィボナッチ数であることが多いです。
🍍パイナップルの螺旋の数は時計回りは13、反時計回りは8になっています。
ちなみにパイナップルは形は松（pine）、味はリンゴ（apple）に似ていることから、パインとアップルでパイナップルになりました。
🐳ハチやアリなど、オスに父親がない家系を辿っていくとフィボナッチ数列が現れます。（父母2匹、祖父母3匹、曽祖父母5匹、高祖父母8匹…。）
おもしろいですね。

まあキリがないのでこのくらいにしましょうか。
そういえば
🔖恩田陸さんの傑作小説『蜜蜂と遠雷』でも、天才少年の風間塵が海辺で巻き貝を拾い「フィボナッチ数列だね」と言うくだりが出てきましたね。
覚えていますか？

蜜蜂と遠雷 (1)

こちらはコミック版です。単行本や文庫版にも飛べます。

🎹音楽と数学

『蜜蜂と遠雷』の話が出てきたのでちょっと脱線して、
🎹音楽と数学はめっちゃ関係がある
ということについて少し語ってみます。
この記事に書いた理論の多く（フィボナッチ数列や、この後で触れる「黄金比」など）は、
実際にクラシック音楽の作曲に使われていたようですよ。
現代のボカロPさんとかはどうなんでしょうかね？
詳しい方はコメントで教えてくださいね。

🎵音階

現在使われている「ドレミファソラシド」を「平均律」と言います。
平均律の祖先は、「ピタゴラス」の定理（三平方の定理、とも言います）で知られるピタゴラス（紀元前582年～ 紀元前496年、古代ギリシア）が考案した「ピタゴラス音律」と呼ばれるものです。

さて、
✅ピタゴラス音律は今のものとは異なり、21音からなります。
なぜでしょうか？

例えば現在では、ド#とレ♭は同じ音として扱われます。
しかし、ピタゴラス音律では似て非なるものとされていました。
ド♭、ド、ド#、レ♭、レ、レ#、ミ♭…と数えていくと、
ドレミファソラシの7音×3種類=21音になるのです。

おもしろいでしょう？

ピタゴラス音律にも、その後につくられた様々な音律にも一長一短があり、
その良いとこどりをする形で現在の「平均律」が作られました。
平均律はオクターブを12等分しているので、
どんな調でも同じ調律で演奏ができるというメリットがあるのです。
こうして、ピタゴラス時代には21音だった音律は、
現在では12音となりました。

⚠️「微分音（半音の半分または1/3）」という、12音から外れた音程も使用されているようですが長くなるのでこの記事では割愛します。

🎹１オクターブは白鍵が７、黒鍵が５、計12音となっていることをお確かめください。
（画像はこちらのサイトより引用）

🎵周波数（振動数）

ちなみに「１オクターブ」にはちゃんとした定義があります。
ある音と、１オクターブ上の音の周波数を比べると、
ちょうど２倍になっているのです。
例えば、ある「ラ」の音を440Hzとした場合、
1オクターブ上の「ラ」は880Hzとなっています。

🎹周波数（振動数）とは？
１秒間に音が振動する回数（より正確に言うと、波動や振動が、単位時間当たりに繰り返される回数）。
単位はHz（ヘルツ）。これが高いほど音の高さも高くなる。

さきほどご説明したとおり１オクターブは12音ですので、
ある音と次の音との周波数比は、
２の12乗根（12回かけ算すると２倍になる値）になっています。

具体的にはいくつなのでしょうか。
関数電卓などを使ってもよいのですが、
簡単なのはExcelの適当なセルに

=2^(1/12)

と入力してみてください。
1.05946309436…と出てきます。
（Excelって何乗根でも計算できるんです！✨）

ざっくりいうと、ド#（＝レ♭）はドの1.06倍、レはそれのさらに1.06倍…
となっていき、12音上（＝オクターブ上）のドは
元のドのちょうど２倍となっているのです。
音楽って、実はめっちゃ数学でもあったのですね。

🎵音符の名称

…ちょっと難しい話が続いてしまったので、
中学レベルの音楽の話をしてみましょう。
定期テストで「音符の名称や長さ」を学習すると思いますが、
アレは丸暗記する必要はまったくありません。

🎹全音符が４拍である

ということだけ覚えておけば、あとは名称をかけ算すればよいのです。
例えば
🎹２分音符…４拍×１/２＝２拍
🎹４分音符…４拍×１/４＝１拍
🎹８分音符…４拍×１/８＝１/２拍
🎹16分音符…４拍×１/16＝１/４拍

という具合ですべて計算で出せます。
…ちょっと脱線するつもりが、長くなってしまいました💧
それでは、話をフィボナッチ数列に戻します。

🍏フィボナッチ数列の一般項と黄金比

高校生以上の方は、
✅フィボナッチ数列の一般項を求められますか？

普通の漸化式の知識で求められます（数字は多少ややこしいですが💦）。
ちなみに答えはこちら。

この、

というの、見たことないですか？

実はこれ、古代から長方形の「黄金比」、
つまり「一番美しい長方形の縦横比」として知られる有名な数字です。

ですね。
√5≒2.23606なので、これは

とも表現することができます。
さてここで、
✅フィボナッチ数列の隣り合う数どうしの比を求めてみてください。

別に難しくありません、2 : 3から始めていきましょう。

2 : 3 ＝ 1 : 1.5
3 : 5 ≒ 1 : 1.666666
5 : 8 ＝ 1 : 1.6
8 : 13 ＝ 1 : 1.625
13 : 21 ＝ 1 : 1.61538
…
いかがですか？
どんどん黄金比に近づいていっているのがわかりましたか？

理系の人であれば
✅フィボナッチ数列の隣り合う２項の比は黄金比に収束していく

ことを高校生でも証明できますので、
我こそはと思う方はやってみてください！✨

🍏階段の昇り方

✅階段を1段または2段ずつ昇るときの昇り方が何通りあるか
について考えてみましょう。

1段めへの行き方は1通り
2段めへの行き方は2通り
（⚠️1段ずつ昇っていく方法と、一気に2段昇る方法、の２通り）

ここまではいいですね。

３段めは、これらを足した３通りになるのがおわかりでしょうか？
いま、階段は1段または2段ずつでしか昇れないのですから、
３段めにいる人は、その手前では
「１段めか２段めのどちらかに必ずいた」からです。

このように、
3≦nにおいて、n段めへの行き方は、

【n-1段めへの行き方の数】+【n-2段めへの行き方の数】通り

あることになります。

１つ前と２つ前を足せば今の数が求まる
…考え方はフィボナッチ数列とまったく同じです。
ただし、フィボナッチ数列は最初の2項が「1,1」であるのに対し、
階段問題では「1,2」で始まることにご注意ください。

ですから、
⚡n 段の階段を1段または2段ずつ昇るときに、昇る場合の数は Fn+1 通りある

ことがわかります。
※Fn+1…フィボナッチ数列の（n+1）番めの項、の意。
ちょっと難しかったでしょうか💦

🍏互いに素

他にも、
✅フィボナッチ数列の隣同士の項は、必ず「互いに素」になる

ということも知られています。
⚠️「互いに素」…2つの整数が1以外に共通の約数を持たないこと。
例えば、「５と８」に共通する約数は１だけですから、「５と８は互いに素である」という言い方をします。

背理法と数学的帰納法を用いれば高校生でも証明できますので、
数学の得意な方こちらもぜひ挑戦してみてください！✨

🍏受験について思うこと

子育て教育部のイベント

ところでこの記事は、こちらのコンテスト出品のために過去作をリライトしたものです。

note大学生であれば、子育て教育部に所属してなくても誰でも参加できるということです。
彩流さんは私が主催しているStudy部部員でもありますし、ちょっと参加してみようと思った次第です。

…このままだと「課題から明らかに外れている」と判断されかねないので、この項ではちょっと受験について語ります。
（取って付けたようでゴメンナサイ🙇‍♀️💦）

数学と私

数学って、高１のⅠAまでは何とかなるんですけど、
高２のⅡBから急にムズイですよね😭
でも理系進学を考えている場合、
ここで三角関数とか指数・対数関数とか当たり前にできるようにしておかないと、数Ⅲがもはや鬼畜レベルなんですよ😱

数Bのベクトルや数列もめっちゃムズかった。
（注：新学習指導要領では、ベクトルは数Cで扱うことになりました。）

でもこの記事で取り上げたフィボナッチ数列とか、数列には興味深い話題も多かったですね。
あと、極限を取ってみるといろんなことがわかるという部分もおもしろかったです。
数学…に限らずですが、勉強ってわかると楽しいですね。
受験についてネガティブな意見を持つ人も多いかもしれませんが、人が勉強する一つのきっかけになるという重要かつ有意義な側面はあると思います。

副教科は内申２倍！

東京都の公立高校入試（一般入試）では、副教科（実技教科）の内申点が２倍の価値を持つんですよ。
不器用でスポーツ音痴の私にはとても不利なルールですよね😭

唯一、人並みにできて好きだったのが「音楽」でした。
合唱部ですし。
この記事でも触れたように、数学っぽくてStudyな要素が強めなトコロも好きでしたね。
４分の４拍子になるようにリズム創作する問題とか、とても楽しかったです。
ありがとう、音楽！🎵

英語スピーキングテストについても一言

東京都ローカルな話が続いて恐縮なんですが、
昨年から都立入試に導入された英語スピーキングテストについても一言。

これは実施に至る経緯や態勢などに大いに問題ありということで、
日本共産党都議団とか宇都宮けんじ先生とか、
野党系の方を中心に批判が多いところです。
私も基本的には反対です。

…ただ、家庭教師・塾講師の立場からすると対策せざるを得ないという面はあります。
そして、敢えて誤解を恐れずに言えばテストの内容自体は良いと思っています。
（まったく問題ないとは言いませんが）

生徒さんもスピーキングテスト対策を通して、
上手に英語を音読できるようになったりとか、
４コママンガを英語で描写したりとか、
「学校でのランチとしてみんなで同じ給食を食べるのと、各自が好きなモノを食べるのはどっちが良いか理由とともに英語で述べる」
とか、そういうことができるようになっていくわけですから。
こんなの、もし受験にスピーキングテストなかったらなかなかやる気になれないと思うんですよね。

受験って、国民の学力・教養のレベルを決めるとても重要な要素の一つだと思うんですね。
だから、ちゃんと学識ある方に勉強内容も入試方式も決めてもらいたい。
🙅‍♀️義務教育は小学校までで十分（某国の副総理）
🙅‍♀️サイン・コサイン（三角関数）なんて人生で使わない（維新の某議員など多数存在）
とか公言できちゃうバカな少しばかり思慮の足りない方には政治の意思決定には関わってほしくないです、私は。

…あ、「主義主張が強すぎ、読んでいて不愉快になる」記事になってしまいそうなので、
この辺で止めときましょう😝💧

今年のスピーキングテストは11/26、もうあと３日後です。
受験する都内在住などの中３生の皆さん、
なかなか難しいとは思うけれど、
英語の腕を磨く機会と思って、楽しむ気持ちも忘れずに頑張ってきてください！🙇‍♀️💕

🍏おわりに

というわけでこの記事では、
11/23「フィボナッチ数列の日」にちなんで、
関連するいろんな話題を取り上げてみました。

久しぶりに、ガッツリと数学を語る記事でございました🍎
人生長くやっているとムショーに微分積分したくなることは誰しもあると思いますけれども😝
今日11/23は数列について学習してみるのもよいと思います。

最後までお読みいただきありがとうございました🙇‍♀️
今後もがんばりますので、励ましのスキ・コメント・フォロー・サポート・おススメ・記事の拡散などしていただけますとめっちゃ嬉しいです。
フォローは100％返します。
今後とも有益な情報発信に努めますので応援よろしくお願いします🙇‍♀️

いやあー、数学って、ホントに楽しいですね。
数学も音楽みたいに「数楽」って名づければいいのに。
…誰だ、「数我苦」だなんて言ってる人は😝
またねー！💕

🔖本屋大賞つながりということで、こちらもぜひどうぞ。

🍂noteでStudy部も私設コンテスト開催中！
この記事も、一応こちらのイベント参加記事の一環でもあります。
こちらはnote大学生でなくても、誰でも参加OK！

🌸🍃This article was written by Koper&Aya , Your Study Partners!🐣💕

🍏アヤ先生から切実なお願い🙇‍♀️💕

Tiktok Liteであなたも私も４０００円Get！

こちらの記事で詳しく解説しています。

あなたも4000円Getできて、しかも私に4000円サポートしていただけるのと同じ効果✨
しかもそれだけではありません。
『TikTok Lite』の友達招待キャンペーンに参加すると、あなたも家族や友人などを招待できるようになり、成功すると１人あたり4000円の追加ボーナスをもらえます。
この機会にぜひお願いします！🙇‍♀️🙇‍♀️🙇‍♀️

サポート大募集

あなたからのスキやコメント、サポート&オススメがとっても励みになっています‼️
いつもありがとうございます🙇‍♀️😊💕

ちなみに、いただいたサポートは
🔖note執筆のための書籍購入、資格検定の受験料など
🍰アヤ先生の胃袋へスイーツ補給
✅スマホ・Wi-Fi代
▶止められたら記事の更新ができなくなってしまいます…ぴえん😱
するのに主に遣わせていただいています🙇‍♀️
⚠️サポートとは、定額（100円・500円・1,000円）または任意の金額をクリエイターさんに投げ銭するnoteの機能です🏅

この記事が少しでも勉強になった、励みになった、おもしろかった、
アヤ先生がんばって！
…と思ってくれたあなた。
ぜひ記事の下にあるサポートボタンをポチッとして、アヤ先生のnote活動を応援してもらえると嬉しいです！💕
１００円でも大変助かります。ぜひお願いします（切実）💦

PayPayでも受け取れます

PayPayでも受け取れます。こちらをタップ、またはQRコードを読み取ってください🙇‍♀️
(リンクとQRコード2023/11/23更新)　

https://qr.paypay.ne.jp/p2p01_wEazBOCuLevVre2U

有料記事も販売中！

自分で言うのもアレですが、生徒さんから絶賛を多数いただいているめっちゃおススメの自信作✨💦
（Twitterで拡散いただけると半額になる制度を導入しています）

その他のご支援いただく方法

Amazonギフトなど、できるだけ多くの手段であなたのお気持ちを受領できるようにしたいと思います。
応援したいけどnoteサポートもPayPayもできない、『TikTok Lite』も既に入れている…という方はお気軽にご相談ください。
（コメントまたはTwitterのDMなどでご連絡ください）

また、金銭的なご支援だけでなく、この記事を拡散いただくのもめっちゃ嬉しいし励みになります。
＊アヤ先生を応援したい、noteが楽しみだと思ってくれた方へ
✅Twitterやnoteのフォローがまだの方は、ぜひお願いします🙇‍♀️
▶フォロバ100%です！💕
✅気に入った記事があればnoteのスキ💓ボタンをpush！🧡
✅誰かにおススメしたいほど気に入った記事があったら、以下の２つに記事のご感想を一言添えてツイート！🧡
・　＠Girls_Study_com
・　この記事や、おススメしたいほど気に入った記事のリンク
これをしてもらえるとめっちゃ嬉しいです😭

たくさんの人に読んでもらいたいので
ぜひ拡散・応援よろしくお願いしますm(*_ _)m💕

🎵数列と言えば…歌になるくらい当時受験生の間で話題になった共通テストの「あの問題」を徹底解説！

🔖アヤの本棚（一部抜粋）

蜜蜂と遠雷(上) (幻冬舎文庫)

蜜蜂と遠雷（下） (幻冬舎文庫)

祝祭と予感 (幻冬舎文庫)

『祝祭と予感』は、『蜜蜂と遠雷』のアナザーストーリーです。
おススメ。

We love note , music , novels , and mathematics!💕

#note #自己紹介 #アヤ先生 #フォロバ100 #フォローしてみて

#小説
#映画
#本
#読書
#蜜蜂と遠雷

#受験
#勉強
#恩田陸
#study
#数学

#音楽
#スピーキングテスト
#数学がすき
#フィボナッチ数列
#入試

※私のnoteにはアフェリエイトリンクが含まれています。