
応用編〈2〉 動かす② 循環型
このnoteでは、偶然を発生させる装置と、その結果をもとに操作する別の装置がある問題を「応用編」としています。
その中でもよく出るタイプの問題が、ループタイプすごろくとでも言うべき、この循環型です。
なぜ、よく出るのかは、この項の最後に。まずは問題とその解き方を見てみましょう。
1辺の長さが1の正五角形ABCDEがある。点Pは最初,頂点Aの上にあり,さいころを投げ出た目の数だけ点Pは頂点Aから正五角形の辺に沿って頂点を移動し,さらに,その移動した頂点から2回目に投げたさいころの目の数だけ正五角形の辺に沿って頂点を移動し止まるものとする。
問1 点Pが反時計回りに移動するとき,次の問いに答えなさい。
(1) 1回目に1の目,2回目に5の目が出たとき,点Pはどの頂点の上に止まるか答えなさい。
(2) 2回さいころを投げた後,点Pが頂点Bの上で止まる確率を求めなさい。

問2 さいころの目が奇数の場合,点Pは反時計回りに移動し,さいころの目が偶数の場合,点Pは時計回りに移動するものとする。このとき,点Pが頂点Bの上で止まる場合は全部で何通りあるか答えなさい。
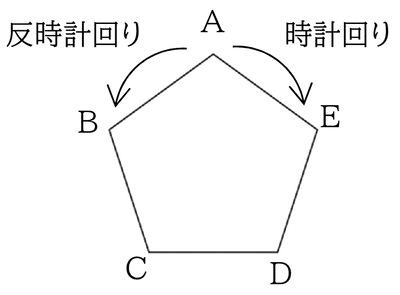
一周回って同じところに止まることがある
点Pが止まる頂点を決めるのは、2回のさいころの目の和、というところに気がついてほしいところですが、(1)はそれを知らなくてもやってみればわかる問題です。
1回目 →B
2回目 →C→D→E→A→B
と1周回ってもう一回Bに止まります。この、一周回って同じところに止まることがあるよ、ということに気づいてもらうための誘導問題、ということでしょう。
(2)を、いろんなアプローチで解いてみる。
(2)は典型問題で、パターン的な解き方はありますが、ここでは、ていねいに一つ一つ考えるところから、考えられるいくつかのアプローチを紹介します。
いちいち調べていると、やっぱり時間がかかるので、「できる人」が、どうやってショートカットしているのか、ということと、でも問2で見るようにパターンが通用しないときのために、パターン化の背景にある複数のアプローチを知っておくことが大切、という例として、ここで紹介していくことにしたいと思います。
アプローチその1 〜1回目はこうだから…
まずは地道に解いていく方法。「できる人」「わかってしまう人」からすると、まどろっこしく感じるやり方かもしれませんが、こうした試行錯誤を紙に残して、目で見ながら前に進めていくやり方はバカにはできません。
さいころ2回なので表というのは、パターンどおりでいいのですが、そこから先、どんな表を書くのか。
表の書き方の一つとして覚えておいてほしいのは、1回目のサイコロの目で、結果がいったんどうなるのかも表に書いておくやり方です。
1回目に出た目を左に、2回目の目を上に書くことにして表をつくり、1回目で点Pを動かした結果も書き添えておくと、表はこんな感じになります。

この左に書いた頂点からそれぞれ出発して、さらに2回目どこに進むかを表のマス目に埋めていくと、こんな表になります。
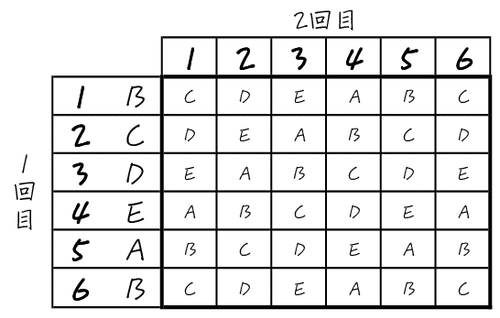
途中で規則性に気づくと、表も埋めやすくなるでしょう。
そう、この規則性を上手につかまえて活かすのが、早く解答にたどり着く近道、ということなのです。このあと、いくつかその近道を見ていくことにしましょう。
アプローチその2 〜2回のさいころの目の和
2つのサイコロやサイコロ2回振って、図形などの上をひたすらぐるぐるまわるという問題は、例年あちこちで出題されます。そして、結局、2回のさいころの目の和の分だけ進む、ということに気づくと、表の各マスに和を書いておく、というやり方も考えられます。

2回のさいころの目の和は2〜12ですので、それぞれに対応する頂点
2→C
3→D
4→E
5→A
6→B
7→C
8→D
9→E
10→A
11→B
12→C
から、頂点ごとの対応
A→5,10
B→6,11
C→2,7,12
D→3,8
E→4,9
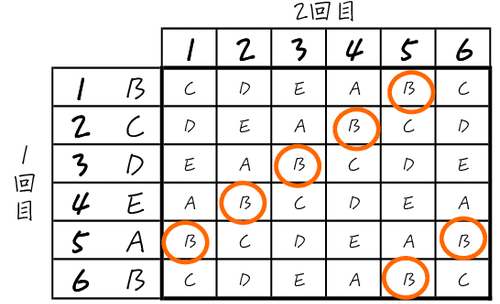
にまとめれば、和が6と11になるところに印を書いて、場合の数を数える、。和が6のところは2つ3つ見つかると、表の中の規則性に気づくのではと思います。
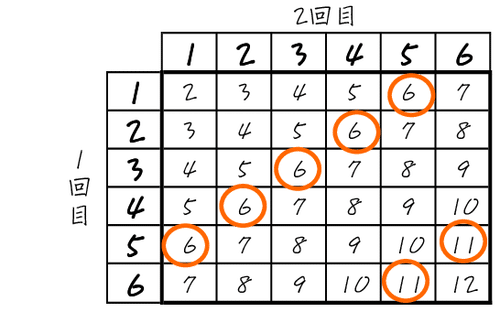
アプローチその3 〜2回のさいころの目の和が6と11だけ表から探す
2回分の和に注目することと、上に書いた和と頂点の対応
B→6,11
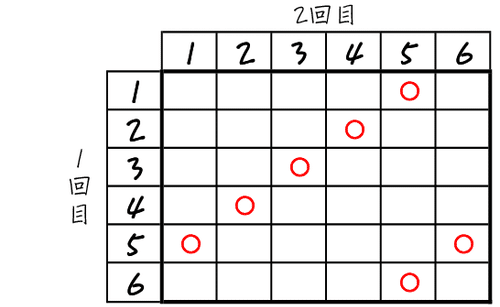
がわかれば、調べればいいのは和が6か11になる場合、ということになります。表の中の各マスで、(いちいち全部の和を計算することをせず)当てはまる場合だけピックアップして、表の中に⚪︎印を書いていく、というやり方で進めてもいいでしょう。
1回目が1のときは・・・2回目は5
2のときは・・・ 4
3のときは・・・ 3
4のときは・・・ 2
5のときは・・・ 1と6
6のときは・・・ 5
アプローチその4 〜2回のさいころの目の和が6と11だけ探す
表は書かないやり方も考えてみましょう。さいころ2回なので表をかかなくても起こりうる同様に確からしいことがらは全部で36通りというのが、バッとわかってしまうと、もうちょっとスピードアップするかもしれません。
(1回目のさいころの目,2回目のさいころの目)の形で、当てはまる場合を書き並べていくことにします。
●和が6になる場合
1と5の組合せ(1,5),(5,1)
2と4の組合せ(2,4),(4,2)
3どうしの組合せ(3,3)
●和が11になる場合
5と6の組合せ(5,6),(6,5)
当てはまる場合は全部で7通り。
なお、このnoteシリーズでは基礎編では表をまず書いてしまうというやり方で解き方を説明してきましたが、当てはまる場合を条件からさかのぼって列挙して、数えるというやり方もあります。高校に入ると、このやり方でないと答えが出ない、というもんだいばかりになります。もちろん中学のタイミングでこのやり方に慣れ親しむ、というのもアリだと思いますが、このnoteのあちこちで主張しているのですが、中学段階ではまず積み木遊びをたっぷりやることかな、と思っていますので、基礎編の中では扱ってはいませんでした。
というわけで、ここでていねいに扱いました。
アプローチその5 〜和を5でわったあまりを考える
この場合、図形上をぐるぐる回る動点の問題は、わり算のあまりに注目するとうまくいきます。
五角形のまわりをぐるぐる回りますので、5でわった余りに注目すると,アプローチ2で書いた対応表は
あまり0 A
あまり1 B
あまり2 C
あまり3 D
あまり4 E
という関係になっていることが分かります。とすると、どこにいるかは、5でわったあまりの数で決まる、ということも言えると思います。
ですから、Bに止まるときを考えることは、和を5でわったあまりが1になる場合を考えることになり、結局は6と11のときを考える、ということになります。
これからさらに上を目指す人は、数学の問題を解く時にこのあまりに注目する場面に出会うと思いますので,発想の引き出しの一つとして身につけておいた方がいいでしょう。
こうした循環型の問題は、わり算のあまりを考えるとうまく行きます。なぜか? わり算のあまりが同じもので作ったグループ分けが、ちょうどグルグル回る点の位置と対応するからです。一番単純なのは偶数奇数ですね。
あまりを使ってグループに分ける方法は、日常でも使われています。例えば体育の時間など、何チームかに分けるとき、例えば5チームに分けるときなど、1列とか輪になってとかで、1,2,3,4,5,1,2,3,‥を順番に言っていくやり方でチームを分ける方法がありますね。誰と一緒になるかドキドキするアレです。
・・・と、こういう風に問題を見てあまりを使う解き方! とパターンにあてはめていくのは、とっても気持ちのよいショートカットに見えますが、それはパターン通りの問題だからです。問2を見てみましょう。
(2)も5つのアプローチでそれぞれ
アプローチ1は両方の「結果」を考える
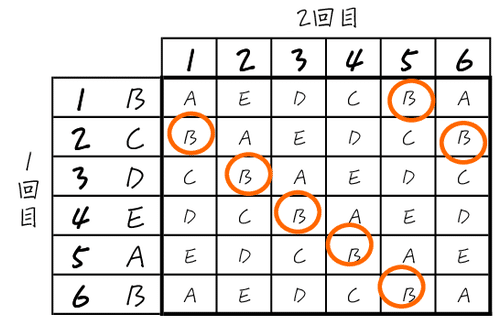
1回目の結果をかいて、そこから2回目の結果を
実はこのアプローチがゴチャゴチャ考えるよりも、今回は早いような気がします。
アプローチ2は和ではなく「差」
1回目と2回目は逆の関係ですので、1回目の目から2回目の目をひいた差を考えてもよいでしょう。5〜ー5ですので、対応表を作ってみましょう。
5→A
4→E
3→D
2→C
1→B
0→A
-1→E
-2→D
-3→C
-4→B
-5→A
となりますので、
A→5,0,ー5
B→1,ー4
C→2,ー3
D→3,ー2
E→4,ー1
あとは、差を書いた表の中で1と-4のところに印をつけます。

アプローチ3は
頂点Bは、1回目の目から2回目の目をひいたときの差が1か-4になる表のマスに印をつけていきます。ひき算なので順序に気をつけましょう。
1回目が1のときは・・・2回目は5
2のときは・・・ 1か6
3のときは・・・ 2
4のときは・・・ 3
5のときは・・・ 4
6のときは・・・ 5
アプローチ4は
和と違って差は順序が入れ替わるとアウトであることに気をつけて。
●差が1になる場合
(2,1),(3,2),(4,3),(5,4),(6,5)
●和がー4になる場合
(5,1),(6,2)
さて、アプローチ5は?
負の数のあまりのあるわり算?ということになります。パターンを覚えて解こうとすると、ここで固まってしまいます。パターン化の悪いところ炸裂です。
いったん5や10をたしてから,とか考えてもいいのですが,このとき方にこだわって,そんなテクニックを使わなくても、他のアプローチの方が素直かも知れません。
これからの数学を学習する上で、いろんなアプローチができる上に、パターンや公式が成り立っていること、そしてそれがストンと当てはまると早い場合もある、けど上位を狙えば狙うほど一筋縄じゃ行かないよ、ということをしっかり肝に銘じておきましょう。
問題を解いた後に
この、わり算のあまりで分類するのは、数学的には、巡回群という構造で、ちょっと高度な数学を反映してみたい、という出題者にとっては、高校入試にちょうど塩梅が良いのかもしれません。
また、円周上に6点とか8点を配置すると、出題者側とすると、融合問題として結構つくりやすいとのかもしれませんね。
類題
岩手県2022 奈良県2022 広島県2022 高知県2022、福島県2021 和歌山県2021、茨城県2020、福岡県2020、愛知県A2019、岡山県2019、宮城県2018、神奈川県2018、島根県2018、熊本県2018B、大分県2018、沖縄県2014(例題採録)、千葉県2013、静岡県2012、山口県2011、兵庫県2010、福島県2009、三重県2009、高知県2009、佐賀県2009、愛知県B2008、鹿児島県2008、滋賀県2007、島根県2007、千葉県2006、長野県2006、秋田県2005、北海道2004、兵庫県2004,京都府2004など
-----------------------
<前の問題 次の問題>
■ 目次 ■
※23.3.5 採録例題を変更
この記事が気に入ったらサポートをしてみませんか?
