高知県（A日程）｜公立高校入試確率問題2022

　右の図のように，[あ]，[い]，[う]，[え]，[お］の５つのマスがあり，こまを［あ］のマスに置く。１個のさいころを２回投げて，下の【ルール】にしたがって，こまを矢印の向きに移動させる。このとき，次の(1)・(2)の問いに答えなさい。ただし，さいころはどの目が出ることも同様に確からしいものとする。

【ルール】
①　１回目に出たさいころの目の数だけ，こまを移動させる。
②　２回目に出たさいころの目の数の３倍の数だけこまを移動させる。ただし，２回目に移動させるときは，１回目に移動させたマスから移動させるものとする。

（例）　１回目に出た目の数が３，２回目に出た目の数が２のとき，こまは次のように動き，［お］のマスに移動する。
・１回目に出た目の数が３より，こまは［あ]→[い]→[う]→[え］と移動する。
・２回目に出た目の数が２より，２の３倍の６だけ移動するため，こまは，［え]→[お]→[あ]→[い]→[う]→[え]→[お］と移動する。

(1)【ルール】にしたがって，さいころを２回投げてこまを移動させたとき，こまが［あ］のマスにある確率を求めなさい。
(2)【ルール】にしたがって，１回目にさいころを投げてこまを移動させたときと，１回目に続けて２回目にさいころを投げてこまを移動させたときとで，こまが異なるマスにある確率を求めなさい。

分類：応用❷　動かす②　循環型

　このnoteのシリーズでは、偶然を発生させる装置とはべつに、その結果を使って操作する別の装置があって、それを使って確率を求める問題を、ここでは「応用問題」として、いくつかのパターンにまとめています。
　こうした応用問題では，それぞれの偶然の結果、何が起こるのか，問題文をしっかり読まなければいけません。

さいころ２回、表には何を書く？

　いろんなところに「さいころは表をかいて考える」と書いてあるのですが、じゃあ、どんな表をかけばよいか、というのは理屈で系統立てて教えてもらえません。解答を見ても、こういうときはこういう表をかけばいいんじゃないの？と例示されるだけです。解答方法の引き出しを増やすのもいいことですが、「なぜその表がいいのか？」「他の方法じゃダメなのか？」と言うことを、少なくとも教える側としてはちゃんと言語化しておいてから、示していく必要性があると思っています。なので、このnoteをただの問題解答、として利用する人としては，何をゴチャゴチャ説明をこねくり回しているの？　と思うかも知れません。

　さてこの場合、スマートに書いてしまうと、１回目に出たさいころの目の数を$${a}$$、２回目に出たさいころの目の数$${b}$$とすると、２回目分のこまの移動は$${a+3b}$$とあらわすことができ、ルール②の$${a+3b}$$を５でわった余りによって、位置が決まります。
　なので$${a+3b}$$を入れてもいいし、$${(a+3b)÷5}$$のあまりを書いてもいいし、このあまりに対応するマスの名前を書けばよいでしょう

‥というふうに解答には書いてあるかもしれませんが、これはあくまで理想。問題文を読んですぐこれを思いつくことを求められるのは、上位層でしょう。そうとかなきゃいけない、というものでもありません。実際には、まずは1→１が出たとき、駒はどのマスにあるか、‥と解きながらあわよくば法則を見つけて楽はできないか考えていく、ということになると思います。
　いろいろと試行錯誤してみましょう。そのときの注意は、試行錯誤した末の、コレ！というものを、試行錯誤途中のものとちゃんと分けて、間違えないようにしておくことです。
　ここでは、マスの名前を各枠に埋めておくのがいいでしょう。

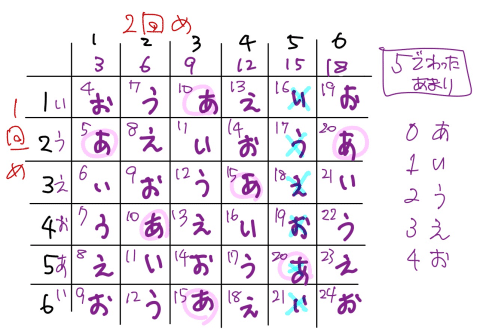
（２）は”じゃない方”から

このように表を埋めておくと、（2）の解き方が楽になります。１回目と２回目が異なる場合の方が圧倒的に多いのです。
　それを数えるとすれば、すべての場合の数は計算で簡単に出るので、そこから「じゃない方」を引いて求めたた方が楽でしょう。表の水色のバツをつけていないところ、36-6=30通り。なので、求める確率は30/36=5/6

答

（１）$${\bm{\dfrac{7}{36}}}$$　　（２）$${\bm{\dfrac{5}{6}}}$$