
#90 分数攻略法:文章題で分数を使った問題を解くスキル
文章題を解くには、順序があります。
その順序を確認していきましょう。
①問題文を読み、内容を理解する。
②理解したことを図に表し視覚的に捉える。
③式を立てる。
④計算する。
文章題を苦手にしている子どもはたくさんいますが、どの段階でつまずいているのかを分析する必要があります。
そしてそのつまずきに合わせて支援しなくてはならないのです。
問題
3分の2dL(デシリットル)で5分の3㎡ぬれるペンキがあります。このペンキ1dL(デシリットル)でぬれる面積は何㎡ですか?
分数が文章題に登場すると、途端に難しくなります。前回は、分数の量感をつかみながら、問題文を理解するところまでお話しました。
今回は、それを可視化する。
つまりわかった量を図に表していきます。
どの教科書も、問題文がでてきたときは、
①問題文を読み、内容を理解する。
②理解したことを図に表し視覚的に捉える。
③式を立てる。
④計算する。
この順序に沿って考えていくように構成されています。
6年生では、読み取れたことを数直線図という図に表していきます。
その数直線図をもとに立式するのです。
子ども達はこの数直線図が苦手です。
なぜか?
答えは簡単です。
小さいころから分かったことを図を使って可視化する訓練をしていないからです。
もしくは、意味がわからず可視化できないまま6年生になってしまったのです。
これは九九暗唱学習の弊害です。
九九暗唱学習の弊害についてはこちらをご覧ください↓
計算領域における図の系統性を簡単に表すと、
1年生
算数ブロックやおはじきを使って具体的に操作したあと、
おだんごの(〇)と←を使って表していきます。
この矢印はポイントです。
〇〇〇〇〇 〇〇〇
→ ←
詳しいことはまたいつかお話する機会があればしたいと思います。
2年生
テープ図やアレイ図を使います。
3年生
テープ図と数直線の合体した図を使います。
量として理解するにはテープ図で、量を数として考えていくために数直線があります。
4年生
テープ図と数直線の合体した図ではじまり、
3学期には数直線図の紹介がされます。
5・6年生
数直線図をつかって問題場面を表し、立式できるようにします。
簡単に整理するとこんな感じです。
今回の問題を図にする場合、下のような数直線図をかくのです。

そして、
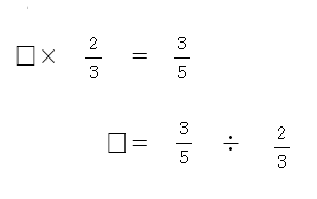
上の数直線図をもとに立式するとこのようになります。
この文章題はわり算になり、数直線図から、答えは5分の3よりは大きくなるという見通しが立つのです。
文章題では、①問題文を読み、内容を理解する。②理解したことを図に表し視覚的に捉える。③式を立てるまでがとても重要であるにもかかわらず、この3つをとばして、いきなり④の計算をしてしう子がなんと多いこと…
これはやはり九九暗唱学習の弊害と言えます。
低学年のうちから、系統的にしっかりと問題場面を図に表すトレーニングすることの大切さを実感できたでしょうか?
何か算数の指導や支援のことで質問や、お困りの方がいらっしゃいましたら、気軽に連絡下さい。
コメントもしくは、クリエーター問い合わせからメールを下さい。

九九暗唱脳を脱却するには、日ごろから論理的思考力を養う必要があります。
論理的思考力が身に付くパズルです。
大人のはまるパズルですよ。
親子で一緒にやってみたらいかがでしょうか?
それではまた。
参考になる方がいたら幸いです。
この記事が気に入ったらサポートをしてみませんか?
