
【ぱわぽdeプレゼン】数学と化学と物理をセッションしてみたら、お米を研いでる時が思い浮かんできたった!
前回のNOTEでやったこと
前回のNOTEでは、数学の素数・合成数(=素数同士を掛け算した数字)を以下のような化学の単原子分子・多原子分子に対応させて分類したら何か面白いことが起こるんちゃうか?っていうことで調べました。
数 学 N 化 学
――――――――――――――――――――
素 数 1 単原子分子
二核合成数 2 二原子分子
三核合成数 3 三原子分子
N核合成数 N N原子分子
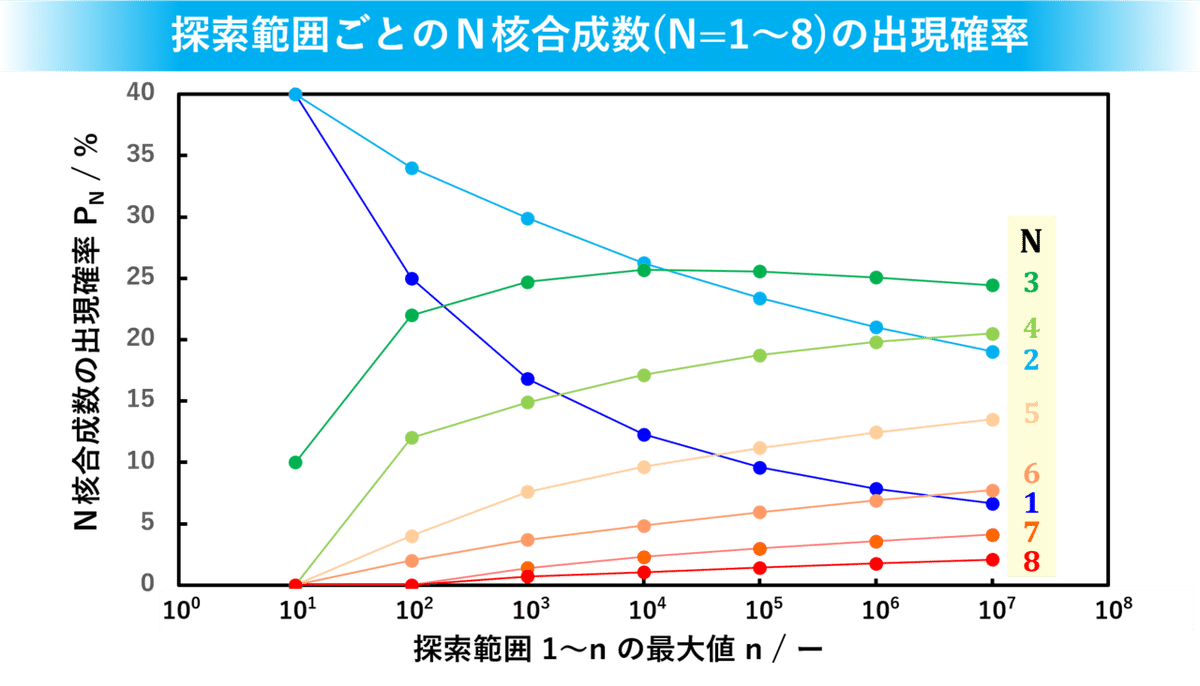
これは2以上の自然数をN核合成数に分類・カウントした時の出現確率のグラフです(便宜上、素数を一核合成数と考えてます)。Nが増えていくごとに山の裾野や頂上を示すようなラインが浮かび上がってきたということまでやりました。今回はこれを眺めていて根拠は無いけど第六感みたいなものが働いたんでそれについて少しだけ語ります。毎度ながら「まぁ不思議ね」っていう体で読んでいただければと思います。
( 'ω' ).。oO( このグラフ、物理の教科書に載ってたような気がするわね
「確か、物理の教科書に似たようなグラフあったよなぁ。活性化エネルギーと頻度因子のアレニウスの式やったっけか?ガラス転位点やったっけか?」って感じで、教科書を見返してみると2つそういう分布がありました。それが気体分子の速度分布を表すマクスウェル分布と、波長とエネルギー密度の関係を表すプランク分布でした。
とりわけ、プランク分布は量子力学の発火点になったイメージがありますね。ある物理実験の結果(黒体放射)を1900年頃の物理レベルでは説明できなかったけど、プランクさんが「エネルギーを量子化したらリアルガチで上手く説明できるで」ってなったんで、そこから今日まで量子力学が発展してきたっていう感じですね。
さて、マクスウェル分布もプランク分布も条件を変えていくとグラフの山が急なものから緩やかなものになるという傾向があります。これが、さっきの「N核合成数の出現確率のグラフと似てるんちゃうの?」と直感しました。そこで今回は、マクスウェル分布の式を使って適当な値を代入してどれだけ似ているのか比べてみることにしました。
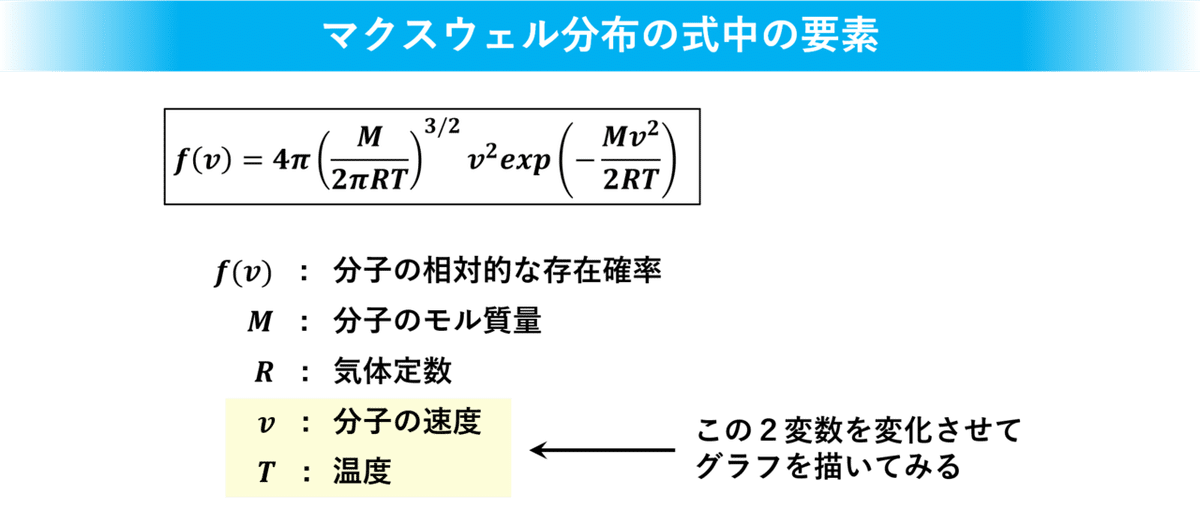
マクスウェル分布のグラフを描くには分子の重さMと分子の速度v、温度Tの3変数が入っているので、どれか1つを固定すれば3次元グラフ、どれか2つを固定すれば2次元グラフを描くことができます。今回はとりあえず分子の重さMを固定した3次元グラフを描いてN核合成数の出現確率のグラフと見比べてみることにします。
マクスウェル分布と似てたわ
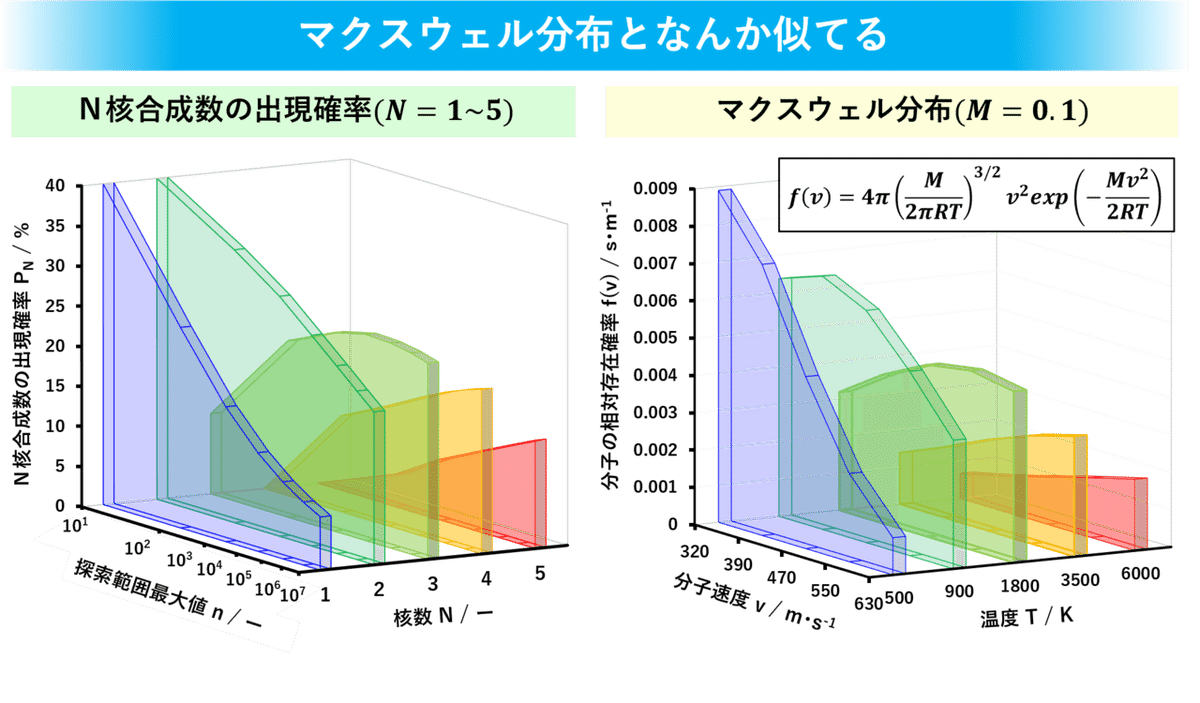
左側がN核合成数の出現確率(N=1~5;冒頭のグラフを3次元化したもの)、右側がマクスウェル分布の一部をぶった切ったものです。結果から言うとよく似てました。ここから言えるのはN核合成数の出現確率Pを表す関数はマクスウェル分布を表す式と似てそうだということですね。検証に使ったマクスウェル分布の場合は変数が(v,T)でしたけど、N核合成数の出現確率Pでは探索範囲の最大値と核数(n,N)に変数が対応しているんでしょうね。
グラフを見てたらお米研いでる時が思い浮かんできたったわ
今回はマクスウェル分布を描くにあたって、分子質量Mを適当な数値(100 g/mol)で固定しましたが、温度Tの軸の項目を質量Mに変えて重たくしたり軽くしたりすることでも似たようなグラフが描けるようです。その場合は、感覚的にはお米を研ぐ時のイメージが浮かんできました。マクスウェル分布を次のように変えましょう。
・分子速度v → 水中を漂う米粒の速度
・温度T → 米粒の重さM
グラフでの変化としては、温度500Kの位置が「米粒=重い」、温度6000Kの位置が「米粒=軽い」という具合になりますね。
お米を研いだ時、重い米粒は直ぐにボウルの底にたまりますが、軽い米粒の破片は研ぐのを止めても沈まないので、水が白く濁ったように見えます。これは、米粒の破片の速度が(相対的に見たら)高速度エリアに集中しているためです。今回プロットしてるエリアがたまたま低速度領域だったので、米粒の破片の存在確率に相当する赤い側の山は低いです。もし、プロットエリアを高速度領域まで拡張してやったら赤い側の山は楯状火山っぽいグラフを描き、高速度エリアでの存在確率が一番高くなります。
一方で、重い米粒の場合は低速度エリアに存在確率がごそっと集中しているので、それに相当する青い側の山はめちゃくちゃ高くなっています(その代わり高速度エリアでは限りなくゼロに近くなる)。「お米を研いでて水中をすごい高速移動してる重い米粒なんかそうそう見れんわな」っていうイメージがそのまんま確率の山に反映されている感じですね。
本編とは関係ありませんけど、お米を研いだら米粒の破片が細胞同士の間にある溝というかすき間に入り込んで(ミクロレベルで見れば凸凹の肌が平らに近づくんで)肌の摩擦を減らすのか知りませんけど、急に手がさらさらになるというかスベスベになったかのように感じますね。お米を研いだ後は、個人的にそれが好きだったりします。
マクスウェル分布の変数を(v,M)にしたら自然数が気体分子に見えてけぇへん?
米粒の速度分布のイメージを書いていてふと気づきました。マクスウェル分布のグラフ化に使う変数を(v,T)ではなく(v,M)にした時、分子の質量によってグラフが変化することになります。

トップ絵の化学のN原子分子のように、原子数が増えれば当然ながら重さも増えていきます。そうなると、N核合成数の出現確率のデータってのは自然数があたかも重さを持った気体分子のように振舞っているって言ってるようなもんじゃね?と思いました。その場合、原子数(N)が大きいほど軽い気体分子のように振舞うのでM∝1/Nという関係なのかもしれません(温度Tとの関係ではT∝Nのように見えましたけどね)。
まとめ
化学の視点から2以上の自然数を素数と合成数に分け、それらが出現する確率Pを3次元グラフにしたところ、物理の世界に瓜二つのグラフ(マクスウェル分布の一部)があることがわかりました。従って、素数と合成数の出現確率Pの関数はそれに似た形の式で表せると予想できます。また、マクスウェル分布の変数を分子速度と分子質量に変えた時、自然数はあたかも重さを持っている気体分子(単原子分子と多原子分子)のように振舞うという面白い見方ができることを見出せました。
( ˘ω˘ ).。oO( そうだと言える根拠はないけど、不思議な結果だわね...。
「ためになるわ」と感じて頂ければサポートを頂ければ幸いです。よろしくお願いいたします。
