
生産者理論(6):生産費用
生産者理論(4)にて、費用最小化問題の解集合としての条件付要素需要関数、価値関数として費用関数を導入した。今回はそれらをベースに、生産者の技術や生産要素の性質を考慮し分析することで生産費用の諸概念を明らかにし、それらの幾何学的関係を整理する。連載はこちら。
生産費用の諸概念
以下の議論では、前回整理した生産集合の5つの性質を仮定し、それぞれ以下の通り生産関数を用いて表現する。
①非空:生産関数$${f: \R_+^N \Rightarrow \R_+}$$が存在する
②閉集合:$${f}$$が連続関数
③フリーランチ不可能:$${f(0)=0}$$
④自由可処分:全ての$${x_i}$$について単調非減少かつ$${y \in [0, f(x)]\Rightarrow (x,y) \in Y}$$(=任意の生産計画の右下方部分が$${Y}$$に含まれる)
⑤必要投入量集合の凸性:$${f}$$は準凹関数
また、長期生産関数においては追加で以下の性質も仮定する。
無生産の可能性:$${(0,0) \in Y}$$
可変費用と固定費用
まず、生産費用の概念として以下の2つを定義する。
可変費用:生産計画期間中に自由に投入量を変化させることができる生産要素の投入にかかる費用
固定費用:生産計画期間中に投入量を変化させることができない固定生産要素の投入にかかる費用。①埋没費用:工場や機械類などの耐久財を自己資金で購入した場合の機会費用、②減価償却費:耐久財の減耗に対する更新投資に伴う費用など、複数計画期間にまたがって発生し、各期の最適化行動が相互に依存するような動学的な費用と、③維持費用:耐久財の整備・維持費用や④経営管理費など、直接生産量に関連しないが、恒常的に投入が必要で、各計画期間において同様に発生する静学的な費用がある。
可変費用と固定費用の分類は、考えている期間の長さによって異なる。例えば工場の大きさが固定されている短期では、工場に係る費用は固定費用であり、自由に雇用量を調整できる労働は可変費用と見なせる。一方、全ての生産要素の大きさを変えられる長期では、全ての費用は可変費用となる。
いま、第1生産要素のみが可変生産要素、残る第$${j(=2, \cdots, N)}$$要素が固定生産要素となる1生産物モデルを考える。固定生産要素の投入ベクトルを$${\bar x_f}$$、固定要素価格ベクトルを$${w_f}$$とすると、固定費用$${C_f}$$は次の通り表せる。
$${C_f(w_f, \bar x_f)\equiv\displaystyle\sum_{j=2}^N w_j \bar x_j}$$
可変生産費用を$${C_v}$$とすると、(総)費用関数$${C}$$は以下で表される。
$${C(y, w_1, w_f, \bar x_f)\equiv C_v (y, w_1, \bar x_f)+C_f(w_f, \bar x_f)}$$
ところで、費用最小化問題の解集合$${z(w,q)}$$を条件付要素需要関数として定義したが、これは生産関数$${y=f(x_1, \bar x_f)}$$について、可変投入量$${x_1}$$についての逆関数$${x_1=z_1(y, \bar x_f)}$$と見なせる。このように定義し直したうえで、費用関数を次のように書き換えることができる。
$${C(y, w_1, w_f, \bar x_f)\equiv w_1z_1(y, \bar x_f)+C_f(w_f, \bar x_f)}$$

限界費用と平均費用
次に、生産費用に関する以下の概念を導入する。
限界費用:限界的に生産物の産出量を変化させた場合の産出量1単位当たりの可変費用の変化量。$${C}$$が$${y}$$について微分可能であるとき、限界費用は$${MC(y)\equiv \dfrac{\partial}{\partial y}C(y, w_1, w_f, \bar x_f)}$$で定義される
平均可変費用:$${AVC(y)\equiv \dfrac{C_v (y, w_1, \bar x_f)}{y}}$$と表され、限界生産性逓減(逓増)の下では右上がり(右下がり)の曲線となる
平均固定費用:$${AFC(y)\equiv \dfrac{C_f (w_f, \bar x_f)}{y}}$$と表され、右下がりの双曲線
平均費用:$${AC(y)\equiv AVC(y)+AFC(y)}$$と表され、限界費用が平均費用を上(下)回る時に右上がり(下がり)となる。つまり、限界費用曲線は平均(可変)費用が最小となる点で平均(可変)費用曲線と交わる
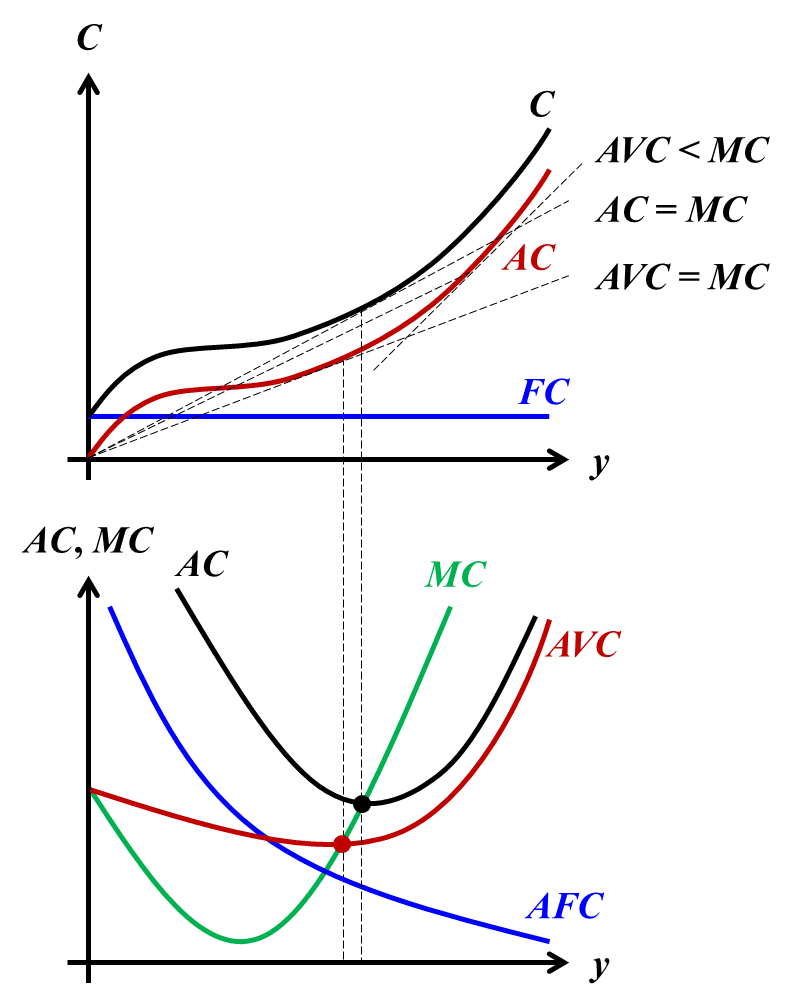
可変生産要素が$${k}$$種類ある場合は、固定要素価格ベクトルを$${w_v}$$とすると、最適投入ベクトルを条件付要素需要関数として以下のように定義できる。
$${z(y, w_v, \bar x_f)=(z_1(y, w_v, \bar x_f),\cdots,z_k(y, w_v, \bar x_f))}$$
この時、費用関数は以下の通り書き換えられる。
$${C(y, w_v, w_f, \bar x_f)= \displaystyle\sum_{i=1}^k w_i z_i(y, w_v, \bar x_f)+\displaystyle\sum_{j=k+1}^N w_j \bar x_j}$$
固定費用は常に一定のため、総生産費用に対する費用最小化問題は$${C_f(w_f, \bar x_f)}$$を除いた可変費用のみを最小化する問題と同値である。従って、以下の最小可変費用関数が最小費用を表す。
$${C_v(y, w_v, \bar x_f)=\displaystyle\sum_{i=1}^k w_i z_i(y, w_v, \bar x_f)}$$
長期費用と短期費用
全ての生産要素が可変$${(k=N)}$$である長期における最小費用は、
$${C(y, w)=\displaystyle\sum_{i=1}^N w_i z_i(y, w)}$$
と表される。この時、長期費用関数と短期費用関数の関係は、次のように表すことができる。
$${C(y, w)=\displaystyle\min_{x_f} C(y, w_v, w_f, x_f)}$$
この最適解を$${z_f(y, w)=x_f^*=(x_{k+1}^*, \cdots, x_N^*)}$$と書けば、
$${C(y, w)=C(y, w_v, w_f, z_f(y, w))}$$
となる。辺々を$${y}$$で微分すると、連鎖律より
$${\dfrac{\partial}{\partial y}C(y, w)=\dfrac{\partial}{\partial y}C(y, w_v, w_f, z_f(y, w))}$$
$${=\dfrac{\partial}{\partial y}C(y, w_v, w_f, x_f^*)+\displaystyle\sum_{i=k+1}^N\dfrac{\partial}{\partial x_i}C(y, w_v, w_f, x_f^*)\dfrac{\partial}{\partial y}z_i(y, w)}$$
となる。ところで、この最小化問題のLagrangianは、
$${L= C(y, w_v, w_f, x_f)+\lambda(y-f(x))}$$
であり、内点解を仮定すれば1階の条件から以下が成り立つ。
$${\dfrac{\partial L}{\partial x_i}=\dfrac{\partial}{\partial x_i} C(y, w_v, w_f, x_f)+\dfrac{\partial}{\partial x_i}\lambda f(x)=0 (i=k+1,\cdots,N)}$$
いま、最適解において$${f(x_f^*)=y=Const.}$$となるため、
$${\dfrac{\partial}{\partial x_i} C(y, w_v, w_f, x_f^*)=0}$$
$${\therefore \dfrac{\partial}{\partial y}C(y, w)=\dfrac{\partial}{\partial y}C(y, w_v, w_f, x_f^*)}$$
となり、以下のことが言える。
長・短期費用曲線の関係
長期の限界費用は、その産出量の下で最適な固定生産要素投入量を選んだ時の短期限界費用に等しく、長期費用曲線は短期費用曲線の下側の包絡線となっている。同様に、長期平均費用曲線も短期平均費用曲線の包絡線である
以上を踏まえて、長期総費用曲線と短期総費用曲線、長期平均費用曲線と短期平均費用曲線、長期限界費用曲線と短期限界費用曲線の6つの生産費用の概念の幾何学的関係を、以下の通りまとめて図示する。
長期総費用曲線$${LC}$$は、短期総費用曲線$${SC}$$の包絡線である
短期平均費用曲線$${SAC}$$、長期平均費用曲線$${LAC}$$はどちらもU字型であり、$${SAC≥LAC}$$である。等号成立時に両曲線は接するため、$${LAC}$$は$${SAC}$$の包絡線である
$${LC=SC}$$となる生産量($${y=y'}$$など)では、短期で固定されている生産要素の大きさが、長期的に見てもその生産量を達成するための最適水準
このような生産量では短期限界費用曲線$${SMC}$$と長期限界費用曲線$${LMC}$$が等しく、曲線の傾きの大きさは$${SMC>LMC}$$
両限界費用曲線$${SMC}$$と$${LMC}$$が交わる生産量において、両平均費用曲線$${SAC}$$と$${LAC}$$は接する

長期限界費用曲線と短期限界費用曲線の幾何学的関係
次回はこちら。
この記事が気に入ったらサポートをしてみませんか?
