
【量子力学誕生の遠因】”エントロピー”をできるだけ分かりやすい言葉で説明してみようチャレンジ
以前に、エントロピーについて自分なりの言葉でまとめたNOTEを書きました。今まで、エントロピーは単に熱力学用語の1つでしかないっていう認識だったわけですが、実は量子力学が生まれるキッカケにもなった概念であることを最近知りました。
よく「乱雑さ」と一言で表現されますが、具体的なイメージが湧かないので今回は「エントロピーについてちょっと知っておこうじゃないのよさ」という感じのNOTEにしました。ヨビノリさんの「【大学物理】熱力学入門④(エントロピー)」を拝見しましたけど、正直難しかったので自分が理解した範囲でまとめました。よかったら最後までお付き合いください ٩( 'ω' )و
1.温度差がある物をくっつけとくとエントロピーは増える(自分的に一番分かりやすい説明)
Wikipediaに載っている熱力学的な説明を使えば、「エントロピーが増えるのは自然(当たり前)なことなんだ」と理解できます。まずは、下のスライドをご覧ください。

外部から一切熱的な影響を受けない箱に熱い物体H(温度TH)と冷たい物体L(温度TL)を閉じ込めて接触させます。すると、いつかはHとLの温度が同じになります。たぶん、この現象は日常生活の中での食事や飲み物、冷暖房などで経験的に知っていることと思います。ちょっと2つの状態を整理してみますね。
状態 [1]
高温物体Hと低温物体Lを接触させた瞬間(熱移動が始まる前)の状態。
状態 [2]
状態 [1] からの熱移動が完結して、温度が均一になった状態。
ここで、H-L間でやりとりした熱量をQとして、エントロピーを表す式S=Q/Tを使うと(二行目の式に書いてます通り)エントロピーの変化量Sが分かります。

注目すべきは式中にH-Lの温度差(TH-TL)が出てくることです。温度の関係はTH>TLなんですから(TH-TL)もエントロピー変化量Sもプラスの値を持つ(S>0、つまりエントロピーは増える)と言えます。
このような「2つの状態を比べた時に、エントロピーが増える方向に状態は変化していくんですよー」ということをエントロピー増大の法則(または、熱力学の第二法則)と言います。分かってしまえば何ともないというか「まぁ、そりゃそうだわな」と感じます。そして、状態 [1] を基準に取れば、2つの状態のエントロピーは次のように書き表せるはずです。

状態 [1] と状態 [2] のエントロピー値を見比べれば、状態 [2] の方向へ変化していくことが分かるので、自分はエントロピーのことを(状態 [1] を基準にした時の)状態 [2] へのなりやすさを数値化したものと勝手に呼んでいます(エントロピーがマイナスであるほど状態 [1] 、プラスであるほど状態 [2] になりやすくなります)。
2.エントロピーに確率統計の考えをぶっこむ
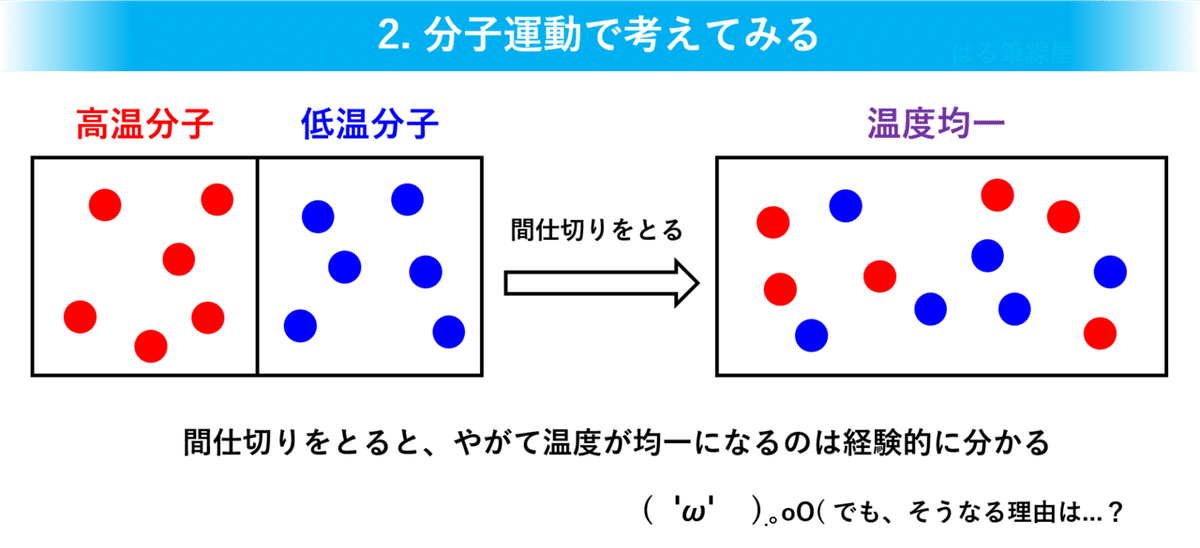
自分が新しく知ったエントロピーの説明は、さっきの熱移動の図を分子運動として見る方法です。高温物体Hは赤い高温分子、低温物体Lは青い低温分子で構成されていて、最初は両者が間仕切りで分断されているものとします。この間仕切りを取っ払って分子たちが自由に行き来できるようにすると、やがては均一な状態(=同じ温度)になるだろうってことが経験的に予想できます。でも、どういった理屈でそうなるのでしょうか?

ここで、高温分子6個に注目してみます。はじめは、間仕切りを隔てて左の空間に6個、右の空間に0個ありました。この状態を(6,0)と表現します。また、均一状態になった後を見ると間仕切りのあった場所を隔てて左右の空間に3分子ずつあるので、この状態を(3,3)と表現しましょう。
均一状態では(3,3)が一番自然に見えるわけなんですけれど、実際は高温分子は運動を続けているのでずっと(3,3)のままでいるわけではありません。ある一瞬を切り取れば(4,2)になっていたり(1,5)になっているはずですよね。

取り得るすべての状態7種を挙げてみました。ついでに、それぞれの分子に1から6まで番号を付けたので、考えられる状態の数をカウントしていきます。(6,0)の場合は図の1通りだけなんですが(5,1)の場合は少し違います。右空間に分子①が入っている状態を1通りとカウントすると、①と②を交換しても同じ状態として1通りカウントできます。また②と③を交換しても1通り、③と④を交換しても1通り・・・というようにすべての取り得る状態の数をカウンティングすると、下のグラフができ上がりました。

棒グラフは左から(6,0)(5,1)(4,2)・・・の順に並んでいて、高さは取り得る状態数(=現実に起こり得るパターン数)を表しています。すべて足し合わせると64通りになりました。
数学的な表現をすれば、1個の分子を左右に振り分ける方法は2通りあることから、N個の分子の取り得る状態数は(2^N)通りあることが分かります。ここではN=6なので W=2^6=64 ですね。
グラフはキレイな山型となり、一番多いのは(3,3)で20通りでした。このことから(3,3)という均一状態が確率的に一番起こりやすく、人はそれを違和感がないものとして見ていると言えるでしょう。”自然さ” の背後には確率が隠れていました。
さて、低温分子も含めて考えた状態数 W は、高温分子の状態数WHと低温分子の状態数WLを使って W=WH×WL(=64×64=4096) 通りあると言えます。最初はそれぞれ同じ空間にあって W=1×1=1だったので、すごく増加しましたよね。このように、起こりえる状態数が多い方へと状態は変化していくと予想できます。状態数とエントロピーの関係性は、どちらも増える方へ状態が変化していくことが共通してそうですね。
3.エントロピーと状態数を結びつけちゃおう
1項、2項で書いてきたことを整理します。
高温物体と低温物体を合わせた時、また高温分子と低温分子を混ぜ合わせた時は次の2つの関係がありました。
エントロピー S=SH+SL
状態数 W=WH×WL
1877年、ボルツマンは「W が掛け算になってるから対数 log を使って足し算の形に直したら、Sと比例関係にあるはずですよ」というボルツマンの原理を発表しました。
S=kB・log W (ボルツマンの原理)
kBはボルツマン定数という比例定数
スライドにまとめると、

ボルツマンの原理のエントロピーは確率統計の考えを基にしているので、エントロピー増大の法則の熱力学的エントロピーと区別して統計力学的エントロピーと呼ばれるそうです。
4.熱力学から統計力学的エントロピーを導こう
今度は、ボルツマンの原理が正しいかを確かめるために熱力学の立場から統計力学的エントロピーを導いてみましょう。使うのは先ほど使った分子たちですが、少し初期条件が違います。

状態 [1]
体積Vの左の空間だけにN個の分子を入れておき(右の空間は真空)、両者の体積が変わらないように間仕切りにストッパーをかけておきます。
状態 [2]
状態 [1] からストッパーを外すと、圧力差によって間仕切りはどんどん右に移動していきます。そして、左の空間がちょうど2倍(体積2V)になった時にストップします。
この時、分子たちは外部から熱的な影響を受けず、真空に対して膨張した(断熱自由膨張)のでエントロピー変化を考えてみます。

熱力学的エントロピーの式と熱力学の第一法則、理想気体の状態方程式を使うと、エントロピーの極小変化量dSはⒶ式のように表せます。

エントロピー変化Sを求めるために状態 [1] から状態 [2] までを積分します。

Ⓑ式の途中では、物質量nを分子数Nに直すためにアボガドロ数NAで割ったり、気体定数R/アボガドロ数NA=ボルツマン定数kBに置き換えるといった操作をしました。Ⓑ式の末尾に注目すると、2^Nという項がでてきました。これは前述したN個の分子を左右の空間に分ける状態数 W と同じなので、2^N=Wとすれば、Ⓒ式のようにボルツマンの原理が導出できます。

表中の状態 [1] と状態 [2] を比較すると、状態 [2] の方が W もSも大きくなるので、断熱自由膨張は自発的に起こることが分かります。また、改めてこの式を統計力学的エントロピーとして眺めた場合、N個の分子が左右の空間にある状態を考えれば(N/2,N/2)という均一状態が確率的に一番起こりやすいだろうということが分かりますね。
5.まとめ
① ある状態変化< 状態 [1] ⇆ 状態 [2] >を考えた時、状態 [2] へのなりやすさを数値で表したのがエントロピーSだと個人的に解釈しました。状態 [1] を基準としたとき、Sがプラスであるほど状態 [2] に、マイナスであるほど状態 [1] になりやすいことを表します。
② 高温物体・低温物体をくっつけた時、また高温分子・低温分子を混ぜ合わせた時、エントロピーは増える方に状態が変化していくことが分かりました(エントロピー増大の法則)
③ 確率統計の考えを基にした統計力学的エントロピーを数式で表すことができました(ボルツマンの原理)
④ 理想気体を用いた断熱自由膨張を考えると、統計力学的エントロピーが熱力学的エントロピーの式から導けることが分かりました
こういう風に確率で物理現象を理解しようという試みは、のちのち量子力学を誕生させるトリガーになったので、個人的には1900年前後が一番科学史で熱いと思っております ( 'ω' ).。oO( 暑い...
「ためになるわ」と感じて頂ければサポートを頂ければ幸いです。よろしくお願いいたします。
