
第7章「心の旅が始まる」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング」の第7章「心の旅が始まる」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
この章では、10の観光地の類似度(距離)を出発点にして、「ベイジアン個人差多次元尺度構成法:INDSCAL」モデルを用いた観光地の2次元座標の推論を行います。

今回のモデルはかなり複雑であり、自己流PyMCモデルはテキストと大きく異なる結果を出力しました(2回連続の汗)
結果はさておき、楽しくPyMCでモデリングして、ベイズ推論を満喫しましょう!
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 小杉考司 先生
モデル難易度: ★★★★★ (難しい)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★★・・& そこそこ \\
結果再現度 & ★★・・・& やや悪い \\
楽しさ & ★★★★・& 楽しそう \\
\end{array}
$$

評価ポイント
テキストの「ベイジアンINDSCALプロット」(図7.2)と全く異なる結果となってしまい、実装精度の★を2つ、結果再現度★を3つ減らしました。
工夫・喜び・反省
INDSCALの数式モデルが初見時に全く意味が分からず、この7章のモデル化を断念するつもりでいました。
ところが、テキスト全19章を1周回して、PyMCテクニックの理解とR+Stanコードの簡便な読み取りが可能になったことで、INDSCALにチャレンジする気力が湧きあがりました。
そして、なんとかモデリングに漕ぎ着けることができ、とても嬉しかったです。
とにかく「実践」することが大事だと、つくづく感じた次第です。

モデルの概要
テキストの調査・実験の概要
425名から得た「10の観光地の類似度」データに基づいて、観光地の座標を推論し、2次元平面にプロットします。
人々はどの観光地が似ている、とか、似ていないと感じているかを図示することが1つの目標です。

観光地は、札幌、飛騨高山、舞鶴、佐世保、志摩、秋吉台、野沢、道後、由布院、宮古島です。
テキストは、年代・性別ごとに分けた10のグループの特徴も考察しています。

テキストのモデリング
■目的変数と関心のあるパラメータ
目的変数$${d_{place1, place2}}$$は2つの観光地の距離を示す「類似度」です。
「似ている0~似ていない10」の11段階で回答者が評価しています。
例えば「札幌」と「飛騨高山」は「類似度5」のような評価です。
なお、実データには0点は無かったです。
観光地は$${place}$$で表記し直しました。
関心のあるパラメータは各観光地の2次元の座標$${\lambda_{place, 1},\ \lambda_{place, 2}}$$です。次元は$${p=1, 2}$$で示されます。
また、年代・性別ごとの重み$${w_{g,p}}$$も押さえておきます。

■個人差多次元尺度構成法(INDSCAL)モデル
インスカルと読むそうです。
この分析では、個人差ではなく、グループ差を分析しているので、「グループ差多次元尺度構成法」的な感じになっています。
ひとまずテキストで明らかになっている数式を並べます。
なお、モデルのコード化時に次元を示す要素の位置が変わります(予告)。
$$
\begin{align*}
d_{place1, place2} &\sim \text{Normal}(\delta_{place1, place2},\ \sigma^2) \\
\delta_{place1, place2, g} &=\sqrt{\sum^2_{p=1}w_{g, p}(\lambda_{place1, p}-\lambda_{place2, p})^2} \\
\sum^P_{place=1} \lambda^2_{place, p} &= 1 \\
\lambda_{place, p} &\sim \text{Normal}(0,\ 1) \\
w_{g,p} &= \sum^G_{g=1} w_{g,p}=G \\
\sigma &\sim \text{HalfStudentT}(\nu=4) \\
\end{align*}
$$
$${\delta_{place1, place2}}$$は2つの観光地の真の類似度です。
$${P}$$は観光地の数です。$${P=10}$$です。
$${G}$$はグループの数です。$${G=10}$$です。
【ちょっぴり補足】
テキストには「技術的な制約」の詳細が掲載されています。
3つの観光地を平面の第一象限・第二象限・第三象限に固定することなどが書かれています。
詳細はテキストをご覧ください。
■分析・分析結果
分析結果はテキストに記載の図表を利用して実施して下さい。
PyMCの自己流モデルはテキストと異なる結果となってしまい、分析に利用できない状況です。

PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.インポート
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')2.データの読み込み
csvファイルをpandasのデータフレームに読み込みます。
### データの読み込み
data_orgn = pd.read_csv('distance_set.csv', header=None)
display(data_orgn)【実行結果】
行インデックスは回答者IDと読み替え可能です。
列0~44が観光地間の類似度、列45が年代・性別のコード値です。
ちなみに、テキストやRコードなどにデータ項目の説明が見当たらないので、ひとまず、私の勘で項目の意味合いを仮置きいたします。

列に観光地の名称を付けてみましょう。
あくまで私の推測に基づく地名設定です。
正確性は担保できません。
### 列名の設定
# 観光地名称のリスト
place_list = ['札幌', '飛騨高山', '舞鶴', '佐世保', '志摩', '秋吉台', '野沢',
'道後', '由布院', '宮古島']
# 観光地x観光地の組み合わせリストの生成
col_names = []
for i in range(len(place_list)-1):
for j in range(i+1, len(place_list)):
col_names.append(f'{place_list[i]}-{place_list[j]}')
# 最後の列は年代・性別
col_names.append('属性')
# 列名の変更
data_orgn.columns = col_names
display(data_orgn)【実行結果】
観光地はこんな感じでしょうか。
また、年代・性別の属性の推測値は次のとおりです。
1:20代男性、2:30代男性、3:40代男性、4:50代男性、5:60代男性、6:20代女性、7:30代女性、8:40代女性、9:50代女性、10:60代女性、

データの前処理をします。
pandasのmeltを利用して縦持ちにします。
### データの前処理
# ID:回答者ID、属性:年代・性別、観光地1・2:類似度を測る2点、類似度:類似度
# データをコピー
data = data_orgn.copy()
# インデックスを個人IDにセット
data = data.reset_index().rename(columns={'index': 'ID'})
# データを縦持ちに変換
data = data.melt(id_vars=['ID', '属性'], value_vars=data.columns[1:46],
var_name='観光地', value_name='類似度')
# 2つの観光地の列を分離
data[['観光地1', '観光地2']] = data['観光地'].str.split('-', expand=True)
# 列の並び替え
data = data[['ID', '属性', '観光地1', '観光地2', '類似度']]
# 加工後データの表示
display(data)【実行結果】
列は、ID:回答者のID、属性、観光地1・2とその類似度になりました。


3.データの外観・統計量
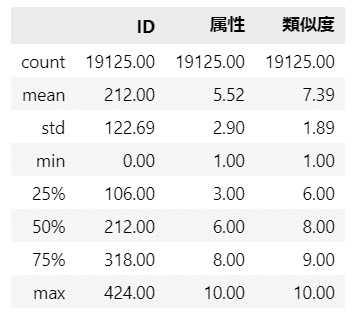
ひとまず要約統計量を確認します。
### 要約統計量の表示
data.describe().round(2)【実行結果】
観光地間の類似度をヒストグラムで確認しましょう。
### 2観光地間の類似度のヒストグラムの描画
# 初期値設定
j = 1
# 描画
plt.figure(figsize=(10, 20))
# 観光地1・観光地2を繰り返して処理
for i, place1 in enumerate(place_list[:-1]):
for place2 in place_list[i+1:]:
plt.subplot(9, 5, j)
# 観光地1・観光地2の組み合わせでデータを絞り込み
tmp = data[(data['観光地1']==place1)&(data['観光地2']==place2)]['類似度']
# 観光地1・観光地2の類似度のヒストグラムを描画
plt.hist(tmp, bins=10)
plt.title(f'{place1}, {place2}')
j += 1
plt.tight_layout()
plt.show()【実行結果】
5以下の回答が全般的に少なく感じます。
値が大きい=類似していないという回答が多いようです。
正規分布に近いのは、飛騨高山・野沢、佐世保・志摩、道後・由布院あたりでしょうか。
この単純な分布がINDSCALでどのように2次元化=地図化されるでしょう。
楽しみです!

モデルの実装
INDSCALモデルの実装です。
事後分布からのサンプリング結果がテキストと相違するようなので、悪いPyMCモデルかもしれません。
PyMCモデリングの参考例くらいのゆるい見方をお願いします。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
テキストおよびStanコードに沿った形です。
添字$${data}$$はデータのインデックスです。
$${fix_{X1}}$$~$${\lambda_{dim, place}}$$が10の観光地の座標$${\lambda_{dim, place}}$$の算出に用いられる分布と計算式です(長いですね~)。
$$
\begin{align*}
fix_{X1} &\sim \text{TruncatedNormal} (\text{mu}=0, \text{sigma}=1, \text{lower}=0, \text{upper}=5) \\
fix_{Y1} &\sim \text{TruncatedNormal} (\text{mu}=0, \text{sigma}=1, \text{lower}=0, \text{upper}=5) \\
fix_{X2} &\sim \text{TruncatedNormal} (\text{mu}=0, \text{sigma}=1, \text{lower}=-5, \text{upper}=0) \\
fix_{Y2} &\sim \text{TruncatedNormal} (\text{mu}=0, \text{sigma}=1, \text{lower}=0, \text{upper}=5) \\
fix_{X3} &\sim \text{TruncatedNormal} (\text{mu}=0, \text{sigma}=1, \text{lower}=-5, \text{upper}=0) \\
fix_{Y3} &\sim \text{TruncatedNormal} (\text{mu}=0, \text{sigma}=1, \text{lower}=-5, \text{upper}=0) \\
raw\lambda &\sim \text{Normal} (\text{mu}=0, \text{sigma}=1, shape=(dim, 6)) \\
const\lambda_{0to8} &= [[fix_{X1}, fix_{X2}, fix_{X3},raw\lambda[0, :]],[fix_{Y1}, fix_{Y2}, fix_{Y3},raw\lambda[1, :]]] \\
const\lambda_9 &= [[0 - sum(const\lambda_{0to8}[0, :])], [0 - sum(const\lambda_{0to8}[1, :])]] \\
const\lambda &= [const\lambda_{0to8}, const\lambda_9] \\
\lambda_{0, place} &= const\lambda_{0, place} / (const\lambda_{0} @ const\lambda_{0}) \\
\lambda_{1, place} &= const\lambda_{1, place} / (const\lambda_{1} @ const\lambda_{1})\\
\lambda_{dim, place} &= [\lambda_{0, place}, \lambda_{1, place}] \\
w_0 &\sim \text{Dirichlet} (\text{a}=ones(dim, attribute)) \\
w_{dim, attribute} &= w_0 * num\_attr \\
\delta_{data} &= \sqrt{w[0, attribute] * (\lambda[0, place1]-\lambda[0, place2])^2 + w[1, attribute] * (\lambda[1, place1]-\lambda[1, place2])^2}\\
\sigma &\sim \text{HalfStudentT} (\text{nu}=4, \text{sigma}=5)\\
likelihood &\sim \text{Normal}(\text{mu}=\delta_{data},\ \text{sigma}=\sigma) \\
\end{align*}
$$
1.モデルの定義
まず、データインデックスを取得しましょう。
属性(年代・性別)attr_idx、観光地place_idx、次元dimです。
### モデルの定義1
## 説明変数のリスト・インデックスattr_idxの作成
# 属性(年代と性別)のリストとインデックスの作成
attr_list = ['20代男性', '30代男性', '40代男性', '50代男性', '60代男性',
'20代女性', '30代女性', '40代女性', '50代女性', '60代女性']
attr_idx = data['属性'] - 1
num_attr = len(attr_list) # stanの「G」に相当する10
# 観光地1、観光地2のインデックスplace_idx1, place_idx2の作成
place_idx1 = data['観光地1'].apply(lambda x: place_list.index(x))
place_idx2 = data['観光地2'].apply(lambda x: place_list.index(x))
num_place = len(place_list) # stanの「I」に相当する10
# 次元2次元のリストの作成
dim_list = ['dim1', 'dim2']
num_dim = len(dim_list)続いてPyMCのモデルを設定します。
coord、data、パラメータの事前分布、尤度をそれぞれ指定します。
## モデルの定義2
with pm.Model() as model:
### データ関連定義
# coordの定義
model.add_coord('data', values=data.index, mutable=True)
model.add_coord('attribute', values=attr_list, mutable=True) # 属性
model.add_coord('attribute3to8', values=[3, 4, 5, 6, 7, 8], mutable=True)
model.add_coord('place', values=place_list, mutable=True) # 観光地
model.add_coord('dim', values=dim_list, mutable=True) # 次元
# dataの定義
y = pm.ConstantData('y', value=data['類似度'], dims=('data'))
attrIdx = pm.ConstantData('attrIdx', value=attr_idx, dims='data')
place1Idx = pm.ConstantData('place1Idx', value=place_idx1, dims='data')
place2Idx = pm.ConstantData('place2Idx', value=place_idx2, dims='data')
### パラメータの事前分布
## λの定義
# 計算1:第一・第二・第三象限制約fixのλ・その他rawLamのλの事前分布の定義
# テキストの図7.2の3つのまとまりを意図的に作り出す
# 第一象限に制限される観光地の座標(0:札幌)
fixX1 = pm.TruncatedNormal('fixX1', mu=0, sigma=1, lower=0, upper=5)
fixY1 = pm.TruncatedNormal('fixY1', mu=0, sigma=1, lower=0, upper=5)
# 第二象限に制限される観光地の座標(1:飛騨高山)
fixX2 = pm.TruncatedNormal('fixX2', mu=0, sigma=1, lower=-5, upper=0)
fixY2 = pm.TruncatedNormal('fixY2', mu=0, sigma=1, lower=0, upper=5)
# 第三象限に制限される観光地の座標(2:舞鶴)
fixX3 = pm.TruncatedNormal('fixX3', mu=0, sigma=1, lower=-5, upper=0)
fixY3 = pm.TruncatedNormal('fixY3', mu=0, sigma=1, lower=-5, upper=0)
# 制限のない観光地の座標
rawLam = pm.Normal('rawLam', mu=0, sigma=1, dims=('dim', 'attribute3to8'))
# 計算2:制約のあるλを設定
# ※tensorにスライス形式で代入できないため、stackとconatenateで変数を繋げる
# 列0~3:0:札幌・1:飛騨高山・2:舞鶴の制限付きλ
constLam0to2 = pt.stack([[fixX1, fixX2, fixX3],
[fixY1, fixY2, fixY3]])
# 列0~8:3:佐世保・4:志摩・5:秋吉台・6:野沢・7:道後・8:由布院の制限なしλの連結
constLam0to8 = pt.concatenate([constLam0to2, rawLam], axis=1)
# 列9:9:宮古島の原点を固定するλを計算してスタック
constLam9 = pt.stack([[0 - pt.sum(constLam0to8[0, :num_place-1])],
[0 - pt.sum(constLam0to8[1, :num_place-1])]])
# 列0~9のλを連結
constLam = pt.concatenate([constLam0to8, constLam9], axis=1)
# 計算3:ノルムを整えてλの完成(Σλ²=1)
# 計算後のλを一時格納するリストの初期化
lam0, lam1 = [], []
# 0次元(x軸)のλの計算
for i0 in range(num_place):
lam0.append(constLam[0, i0] \
/ pt.sqrt(pt.dot(constLam[0, :], constLam[0, :])))
# 1次元(y軸)のλの計算
for i1 in range(num_place):
lam1.append(constLam[1, i1] \
/ pt.sqrt(pt.dot(constLam[1, :], constLam[1, :])))
# 0次元・1次元を連結してλの完成
lam = pm.Deterministic('lam', pt.stack([lam0, lam1], axis=0),
dims=('dim', 'place'))
## 属性グループ差の重みwの定義
# 初期値の事前分布の定義(確率の合計が1になるディリクレ分布を利用)
w0 = pm.Dirichlet('w0', a=np.ones((num_dim, num_attr)),
dims=('dim', 'attribute'))
# 属性数を乗じてwの完成(Σω=10)
w = pm.Deterministic('w', w0 * num_attr, dims=('dim', 'attribute'))
## 本当の距離deltaの定義:尤度の正規分布のmu
delta = pm.Deterministic('delta',
pt.sqrt(
w[0, attrIdx] * pt.sqr(lam[0, place1Idx] - lam[0, place2Idx]) \
+ w[1, attrIdx] * pt.sqr(lam[1, place1Idx] - lam[1, place2Idx])
), dims='data')
# sigmaの定義:尤度の正規分布のsigma
sigma = pm.HalfStudentT('sigma', nu=4, sigma=5)
## 尤度
likelihood = pm.Normal('likelihood', mu=delta, sigma=sigma, observed=y,
dims='data')【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次を設定しました行の座標:名前「data」、値「行インデックス」
属性(年代・性別)の座標:名前「attribute」、値「年代・性別」(10個)
観光地の座標:名前「place」、値「観光地」(10個)
次元の座標:名前「dim」、値「dim1, dim2」
dataの定義
目的変数$${y}$$:類似度、説明変数$${attr\_idx}$$(年代・性別のインデックス)、説明変数$${place1\_idx}$$(観光地1のインデックス)、説明変数$${place2\_idx}$$(観光地2のインデックス)を設定しました。パラメータの事前分布
モデルの数式表現のとおりに設定しました。λ, w, δの定義はStanコードを参考にしてPyMCの制約を加味して書きました。
INDSCAL+技術的な制約が込められています(いると思います)。
PyMCはスライスした配列に代入できないらしいので(私が知らないだけかもしれませんが…)、リスト、stack、concatenateを多用して、なんとか配列を組み立てました(汗)
w0は合計が1になるという制約があり、Stanでは変数定義で取りうる範囲を指定できるところを、PyMCでは変数定義による定義ができなさそうなので(私が知らないだけかもしれませんが2…)、ディリクレ分布で代用してみました。
尤度
正規分布です。次元は「data」です。

2.モデルの外観の確認
### モデルの表示
model【実行結果】
lamのややこしい定義が表示されないですね(寂)

### モデルの可視化
pm.model_to_graphviz(model)【実行結果】
大きなグラフになりました。

3.事後分布からのサンプリング
乱数生成数については、drawsはRスクリプトの数に合わせました。
tune(バーンイン期間)は収束を目指してテキストよりも増やしています。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ55分でした。長時間かかるのでご注意ください。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 55分
with model:
idata = pm.sample(draws=5000, tune=10000, chains=4, target_accept=0.95,
nuts_sampler='numpyro', random_seed=1234)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
rhat_idata = az.rhat(idata)
(rhat_idata > 1.1).sum()【実行結果】
$${\hat{R} > 1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。
パラメータ等の事後分布の要約統計量です。
観光地の座標$${\lambda}$$と$${\sigma}$$です。
### 推論データの要約統計情報の表示
var_names = ['lam', 'sigma']
pm.summary(idata, var_names=var_names, hdi_prob=0.95)【実行結果】
後ほど2次元空間に観光地の座標をマッピングしてモデル化の成否を確認しましょう。

続いて年代・性別別の重み$${w}$$です。
### 推論データの要約統計情報の表示
var_names = ['w']
pm.summary(idata, var_names=var_names, hdi_prob=0.95)【実行結果】
後ほど重みのプロットでモデル化の成否を確認しましょう。

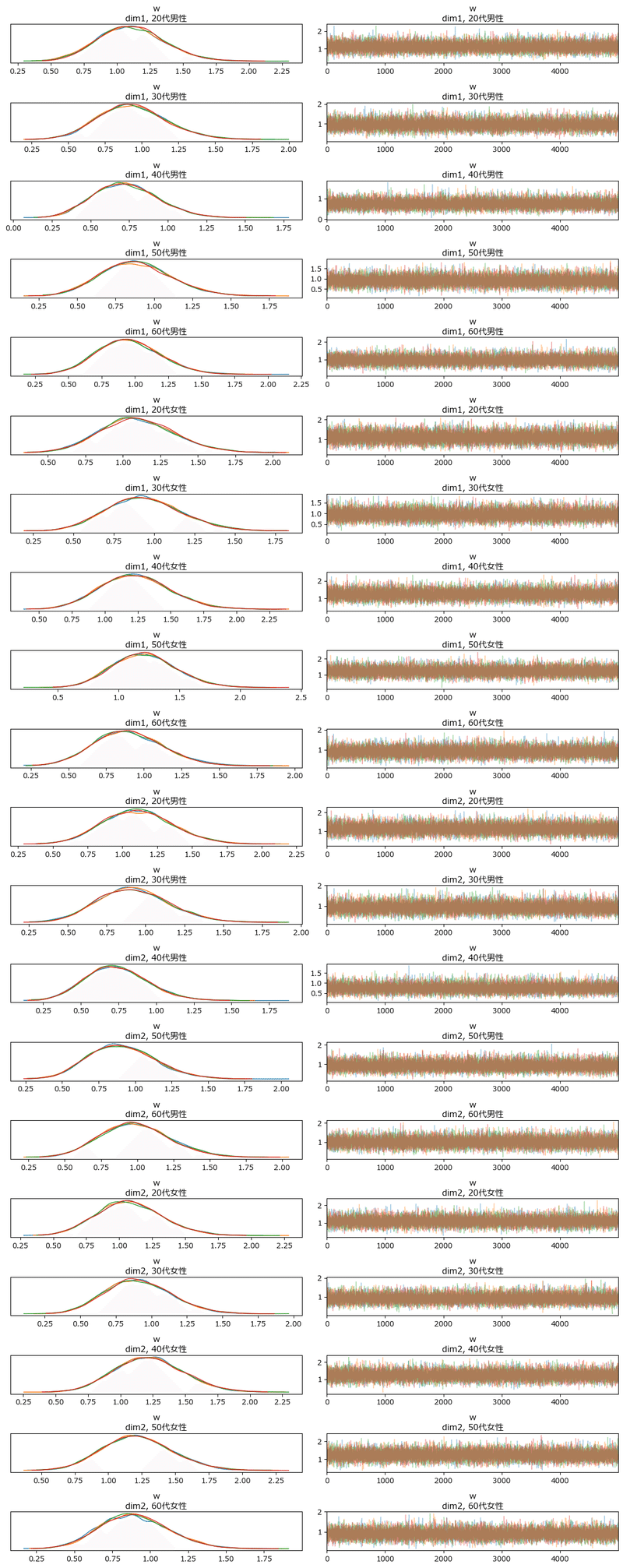
トレースプロットを確認しましょう。
観光地の座標$${\lambda}$$です。
### トレースプロットの表示
var_names = ['lam']
pm.plot_trace(idata, var_names=var_names, combined=False, compact=False,
figsize=(12, 30))
plt.tight_layout();【実行結果】
収束していると考えられます。
(少々、多峰があるのが気になります・・・)

年代・性別の重み$${w}$$です。
### トレースプロットの表示
var_names = ['w']
pm.plot_trace(idata, var_names=var_names, combined=False, compact=False,
figsize=(12, 30))
plt.tight_layout();【実行結果】
収束していると考えられます。
5.分析~テキストにならって
ベイジアンINDSCALによる共通布置のプロット
いよいよ分析コードに移ります!
「心の地図」の可視化を試みます。
テキストの図7.2を代替します。
### 観光地の座標の推定値(平均値)と100件のサンプルのプロット ★図7.2の対応
## データの準備
# 観光地の座標の平均値
lam_mean = idata.posterior.lam.mean(('chain', 'draw')).data
# 観光地の座標の50%信用区間
lam_50 = np.quantile(idata.posterior.lam.stack(sample=('chain', 'draw')).data,
[0.25, 0.75], axis=2)
# 観光地の座標サンプリングデータより各観光地100件抽出
thinned_idata = idata.sel(draw=slice(None, None, 200))
thinned_lam = thinned_idata.posterior.lam.data.reshape(100, 2, 10)
# グラフの色
colors = ['blue', 'red', 'tomato', 'purple', 'gray', 'orange', 'green',
'darkblue', 'brown', 'magenta']
# グラフのマーカー
markers = [',', 'o', 'v', '^', '<', '>', 'p', '*', 'H', 'd']
## 描画
plt.figure(figsize=(6, 6))
# 観光地ごとにプロット
for i in range(num_place):
# 推定値(平均値)の描画
plt.plot(lam_mean[0, i], lam_mean[1, i], 'o', color=colors[i])
# x軸の50%信用区間の描画
plt.plot(lam_50[:, 0, i], [lam_mean[1, i], lam_mean[1, i]],
color=colors[i])
# y軸の50%信用区間の描画
plt.plot([lam_mean[0, i], lam_mean[0, i]], lam_50[:, 1, i],
color=colors[i])
# 座標サンプルデータの描画
plt.scatter(thinned_lam[:, 0, i], thinned_lam[:, 1, i], marker=markers[i],
s=10, color=colors[i], label=place_list[i])
# 観光地の名称の表示
plt.annotate(place_list[i], xy=(lam_mean[0, i]+0.01,
lam_mean[1, i]+0.01))
# 修飾
plt.grid()
plt.xlim(-0.65, 0.65)
plt.ylim(-0.65, 0.65)
plt.title('INDSCALプロット')
plt.xlabel('dim1')
plt.ylabel('dim2')
plt.legend(bbox_to_anchor=(1, 1))
plt.show()【実行結果】
テキストと全然違います(泣)
クリスマスリースのように美しい円環が浮かび上がりました!という絵的な部分で喜んでおきます(笑)
PyMCのモデリング時に、第一象限に札幌、第二象限に飛騨高山、第三象限に舞鶴を固定しました。
この固定が影響して、札幌と飛騨高山が近くにならなかったのでは?、と考察しました。

この図には、野沢・飛騨高山グループ、道後・由布院・秋吉台グループ、志摩・佐世保グループが見られます。
dim1はマイナスが温泉、プラスが海鮮美味、みたいな感じでしょうか。
dim2は何でしょう?プラス側は山間部で寒い地域、マイナス側は海側で温暖な地域、0付近は海近の温暖な地域、のような感じに見えます。
続いて、年代・性別ごとの重みを可視化します。
表7.3と図7.4の左のグラフを代替します。
### 回答群ごとの次元の重みの表示 ★表7.3の対応
## データの準備
# 男性 dim1
m1 = idata.posterior.w.mean(('chain', 'draw')).data[0, 0:5]
# 男性 dim2
m2 = idata.posterior.w.mean(('chain', 'draw')).data[1, 0:5]
# 女性 dim1
w1 = idata.posterior.w.mean(('chain', 'draw')).data[0, 5:]
# 女性 dim2
w2 = idata.posterior.w.mean(('chain', 'draw')).data[1, 5:]
## データフレーム化
m_df = pd.DataFrame({'dim1': m1, 'dim2': m2}, index=attr_list[:5]).T
w_df = pd.DataFrame({'dim1': w1, 'dim2': w2}, index=attr_list[5:]).T
## データフレームの表示
display(m_df.round(3))
display(w_df.round(3))【実行結果】
こちらの推測値はテキストにやや近い結果となりました。

### 年齢・性別と次元ごとの重みの違いの描画 ★図7.3に対応
# データの準備 x軸のリスト
age_list = ['20代', '30代', '40代', '50代', '60代']
# 描画
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4), sharex=True)
# dim1の描画
ax1.plot(age_list, m_df.loc['dim1', :], label='男性')
ax1.plot(age_list, w_df.loc['dim1', :], label='女性')
ax1.set_title('dim1')
# dim2の描画
ax2.plot(age_list, m_df.loc['dim2', :], label='男性')
ax2.plot(age_list, w_df.loc['dim2', :], label='女性')
ax2.set_title('dim2')
# 修飾
fig.suptitle('年齢・性別と次元ごとの重みの違い')
fig.supxlabel('年代')
fig.supylabel('重み')
plt.legend(bbox_to_anchor=(0.25, -0.15), ncol=3)
plt.show()
【実行結果】
おおむねテキストと同じ傾向を示しています。

【分析】
次元1も2も似た形状をしています。
男性は20代が上のピークであり、40代まで下がり続け、その後60代まで上昇します。
女性は30代で下がるも40代・50代がピークとなり、60代で激減します。
観光に対するミドルエイジの価値観が男女で大きく乖離しているような感じがします。
おじさまの皆さん、ぜひ旅行を楽しみましょう!
有給取りましょう!夫婦で出かけましょう!

6.推論データ(idata)の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idataをpickleで保存します。
### idataの保存 pickle
file = r'idata_ch07.pkl'
with open(file, 'wb') as f:
pickle.dump(idata, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata_ch07.pkl'
with open(file, 'rb') as f:
idata_load = pickle.load(f)以上で第7章は終了です。
図7.4は省略しました。

おわりに
PyMCの旅
私は今、心理学のさまざまなベイズモデリングをPyMCで旅しています。
観光地のような華やかさや、美味しさは得られないですが、新しい景色を眺めて感動できている点が本当の旅と似ていると思います。
R+Stanを用いれば円滑にテキストの研究を体感できるかもしれません。
しかし、Python+PyMCとともに歩みたいのです。
別の言語・パッケージを手掛けられる程にはベイズを理解できていないですし、PyMCは個人的にシンプルで素晴らしい仕組みと思っています。
もしかすると、西城秀樹さんがPyMCを絶賛していたことに影響されているかもしれません。
素晴らしい、PyMCで~♪
素晴らしい!
あ~、だから今夜だけは~♫
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析トピックを PythonとPyMC Ver.5で取り組みます。
豊富なテーマ(お題)を実践することによって、PythonとPyMCの基礎体力づくりにつながる、そう信じています。
日々、Web検索に勤しみ、時系列モデルの理解、Pythonパッケージの把握、R・Stanコードの翻訳に励んでいます!
このシリーズがPython時系列分析の入門者の参考になれば幸いです🍀
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
ベイズ書籍の実践記録も掲載中です。
最後までお読みいただきまして、ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
