
第6章「男心をくすぐるデート戦略」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング」の第6章「男心をくすぐるデート戦略」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
今回の章では、時間で変化するデートの魅力、今日のデートと後日のデートでは魅力に違いがあるかについて、遅延割引関数を活用した階層ベイズモデルで分析しています。

今回のモデルは少々複雑であり、自己流PyMCモデルはテキストと少々異なる結果を出力しました(汗)
結果はさておき、楽しくPyMCでモデリングして、ベイズ推論を満喫しましょう!
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 坂本次郎 先生
モデル難易度: ★★★★・ (やや難しい)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★★・・& そこそこ \\
結果再現度 & ★★★・・& そこそこ \\
楽しさ & ★★★★★ & 楽しい! \\
\end{array}
$$

評価ポイント
テキストおよびStanスクリプトにモデル&数式の詳細な記述があり、PyMCのモデルを描きやすかったです。
しかし、事後分布からのサンプリングデータはテキストの選択確率(グラフ描画)と異なる結果となってしまい、実装精度・結果再現度ともに★を2つ減らしました。

工夫・喜び・反省
テキストでは2つの「わくわく割引モデル」で分析していますが、この記事では「制限付き総和型わくわく割引モデル」の1つのみモデリングしました。主として時短目的です。
モデル内の$${V, \gamma}$$をStanスクリプトを参照して書き換えると「総和型わくわく割引モデル」のモデリングができると思います。
モデルの概要
テキストの調査・実験の概要
「いつのデートに誘うのが最も効果的か」について、恋する乙女にアドバイスを贈ることが目的だ。もちろん、データに基づいて進言しよう。ベイズモデリングだって駆使する。乙女の恋が成就するかもしれないのだから。そう思って、決意した。本章執筆者は本気を出す。
私はこの章を実践する際、ベイズモデリングの新しいモチベーションのあり方について、思いを巡らせました。
主観的な事前動機も大切なのかなって。
いますぐデートを楽しみたいか、待つことの「わくわく」する魅力を感じながら後日のデートを楽しみにするか、みたいなことを想像しながら、実験の概要をご覧ください。

データには「実験参加者9名x今日のデートのモデル4名x後日のデートのモデル4名x遅延日数5日=720通り」が含まれています。
心理学や行動経済学などの分野で広く研究されている「遅延価値割引」(時間が経過するほど心理的価値が低下すること)をモデルに組み入れて、いつに予定するデートが最もわくわくするのか、わくわく割引モデルをベイズモデリングで探ります!

テキストのモデリング
■目的変数と関心のあるパラメータ
目的変数$${C_{ijt}}$$はデートを今日する:0、後日する:1の2値を持つ「後日フラグ」です。
関心のあるパラメータは後日デートする確率$${\theta_{ijt}}$$です。
添字$${i}$$は実験参加者のID($${i=1, \cdots, 9}$$)、$${j}$$はモデルのID(実際にはデータに無い変数)、$${t}$$は後日デートすると選択した場合の遅延日数($${t=1,\ 3,\ 7,\ 13,\ 30}$$)です。
■階層ベイズモデル
すごく長いモデルです!
$${V_{ijt}}$$が「制限付き総和型わくわく割引モデル」の核となる「遅延割引関数」、$${\gamma_i}$$が割引係数(割引率)です。
パラメータの事前分布もすべて定義されています!
$$
\begin{align*}
C_{ijt} &\sim \text{Bernoulli}\ (\theta_{ijt}) \\
\theta_{ijt} &= \cfrac{1}{1 + \exp(\beta_i\ (U_{ij}-V_{ijt}))} \\
U_{ij} &= A_{ij} \\
V_{ijt} &= \alpha_i \cdot \gamma^t_i \cdot \sum^{t-1}_{k=0}\gamma^t_i \cdot A_{ij} + A_{ij} \cdot \gamma^t_i \\
\alpha_i &\sim \text{Normal}\ (\mu_{\alpha},\ \sigma_{\alpha})\ I[0,\ 1] \\
\beta_i &\sim \text{Normal}\ (\mu_{\beta},\ \sigma_{\beta})\ I[0,\ \infty] \\
\gamma_i &\sim \text{Normal}\ (\mu_{\gamma},\ \sigma_{\gamma})\ I[0,\ 1] \\
\mu_{\alpha},\ \mu_{\gamma} &\sim \text{Normal}\ (0.5,\ 0.5)\ I[0,\ 1] \\
\mu_{\beta} &\sim \text{Normal}\ (0,\ 10)\ I[0,\ \infty] \\
\sigma_{\alpha},\ \sigma_{\beta},\ \sigma_{\gamma} &\sim \text{StudentT}\ (\text{nu}=3,\ \text{mu}=0,\ \text{sigma}=1)\ I[0,\ \infty] \\
\end{align*}
$$

■分析・分析結果
PyMCのモデリング対象は「制限付き総和型わくわく割引モデル」といたします。
分析結果はテキストに記載のとおりです。
PyMCモデリングでの分析結果は、「PyMC実装」章の【分析】の部分をご覧ください。
PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.インポート
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')2.データの読み込み
csvファイルをpandasのデータフレームに読み込みます。
### データの読み込み
data = pd.read_csv('data.csv')
display(data)【実行結果】
「ID」は実験参加者のIDです。
「C」はデートを今日すると回答:0、後日すると回答:1です。
「U」は「今日のデート画面」のモデルに対する好み度(0~100)
「A」は「後日のデート画面」のモデルに対する好み度(0~100)
「Delay」は後日のデートまでの遅延日数(1, 3, 7, 13, 30日後)です。

3.データの外観・統計量
ひとまず要約統計量を確認します。
### 要約統計量の表示
data.describe().round(2)【実行結果】

ヒストグラムも確認しましょう。
### ヒストグラムの描画
plt.figure(figsize=(12, 4))
for i, col in enumerate(data.columns[1:]):
plt.subplot(1, 4, i+1)
plt.hist(data[col], bins=20, edgecolor='white')
plt.title(f'{col}')
plt.tight_layout()
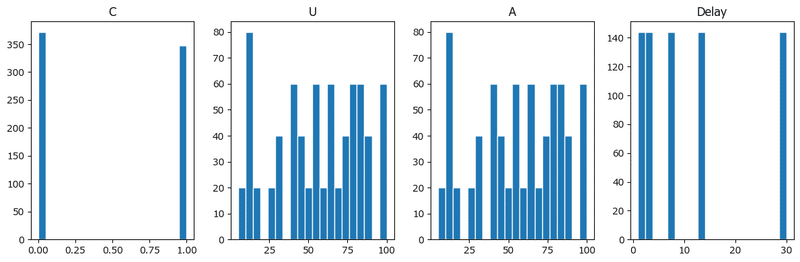
plt.show()【実行結果】
Cは今日・後日が半々程度です。
UとAは形状がよく似ています。
後日デートの場合の遅延日数は均等です。
テキストの図6.2の後日のデート選択比率の可視化です。
0日時点の描画は省略しました。
まずはID別から。
### 後日のデートの選択比率 ★図6.2に対応
# Cの平均(比率)を算出
ratio = data.groupby(['ID', 'Delay'])['C'].mean().reset_index()
# 描画
plt.figure(figsize=(6, 6))
# IDごとに描画処理を繰り返し実施
for i in sorted(ratio.ID.unique()):
# ID:iを取り出し
plot_tmp = ratio[ratio['ID']==i]
ax = plt.subplot(3, 3, i)
# Cの平均の折れ線グラフの描画
ax.plot(plot_tmp['Delay'], plot_tmp['C'])
# 0.5の水平線の描画
ax.axhline(0.5, color='black', ls='--', lw=0.8)
# 修飾
ax.set_ylim(-0.1, 1.1)
ax.set_xticks([0, 10, 20, 30])
ax.set_title(f'ID:{i}')
if i==4:
ax.set_ylabel('遅延選択肢の選択比率(個人ごと)')
elif i==8:
ax.set_xlabel('デートまでの日数')
plt.tight_layout()
plt.show()【実行結果】
全て0.5を超える個人ID1と4は後日デートの志向が高い感じです。
反対に全て0.5を下回る個人ID2・3・8・9は今日(いますぐ)デートの志向が高い感じです。
ID6・7は遅延日数が大きくなるにつれて今日のデートの割合が高くなっています。

続いて参加者全体。
### 後日のデートの選択比率 ★図6.2に対応
# Cの平均(比率)を算出
ratio_all = data.groupby(['Delay'])['C'].mean().reset_index()
# 描画
plt.figure(figsize=(4, 4))
# Cの平均の折れ線グラフの描画
plt.plot(ratio_all['Delay'], ratio_all['C'])
# 0.5の水平線の描画
plt.axhline(0.5, color='black', ls='--', lw=0.8)
# 修飾
plt.title('後日のデートの選択比率(全体)')
plt.ylabel('遅延選択肢の選択比率(全体)')
plt.xlabel('デートまでの日数')
plt.tight_layout()
plt.show()【実行結果】
1日後のデートを最も選択しやすい=1日後にデートを誘うとデート成功率が高い、というようなグラフになっています。

モデルの実装
「制限付き総和型わくわく割引モデル」を実装します。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
テキストおよびStanコードに沿った形です。
添字$${data}$$はデータのインデックスです。
下限・上限付きの正規分布は切断正規分布$${\text{TruncatedNormal}}$$、下限0の$${t}$$分布は半$${t}$$分布$${\text{HalfStudentT}}$$を利用します。
$$
\begin{align*}
\mu_{\alpha},\ \mu_{\gamma} &\sim \text{TruncatedNormal}(\text{mu}=0.5,\ \text{sigma}=0.5,\ \text{lower}=0,\ \text{upper}=1) \\
\mu_{\beta} &\sim \text{TruncatedNormal}(\text{mu}=0,\ \text{sigma}=10,\ \text{lower}=0) \\
\sigma_{\alpha},\ \sigma_{\beta},\ \sigma_{\gamma} &\sim \text{HalfStudentT}(\text{nu}=3,\ \text{sigma}=1) \\
\alpha_i &\sim \text{TruncatedNormal}(\text{mu}=\mu_{\alpha},\ \text{sigma}=\sigma_{\alpha},\ \text{lower}=0,\ \text{upper}=1) \\
\beta_i &\sim \text{TruncatedNormal}(\text{mu}=\mu_{\beta},\ \text{sigma}=\sigma_{\beta},\ \text{lower}=0) \\
\gamma_i &\sim \text{TruncatedNormal}(\text{mu}=\mu_{\gamma },\ \text{sigma}=\sigma_{\gamma },\ \text{lower}=0,\ \text{upper}=1) \\
U_{data} &= A_{data} \\
V_{data} &= \alpha_i \cdot \gamma_i^t \cdot A_{data} \cdot (1-\gamma_i^t) / (1-\gamma_i) + A_{data} \cdot \gamma_i^t \\
\theta_{data} &= \text{invlogit} (- \beta_i \cdot (U_{data} - V_{data}))\\
likelihood &\sim \text{Bernoulli}(\text{p}=\theta_{data}) \\
\end{align*}
$$
1.モデルの定義
初期値、coord、data、パラメータの事前分布、尤度をそれぞれ指定します。
データの実験参加者「ID」のラベルは0始まりになるようにデータ加工しました。
### モデルの定義
# 初期値設定 IDを0始まりに修正
idx_i = data['ID'] - 1
# モデルの定義
with pm.Model() as model1:
### データ関連定義
# coordの定義
model1.add_coord('data', values=data.index, mutable=True)
model1.add_coord('id', values=data['ID'].unique(), mutable=True)
# dataの定義
C = pm.ConstantData('C', value=data['C'].values, dims='data')
A = pm.ConstantData('A', value=data['A'].values, dims='data')
DELAY = pm.ConstantData('DELAY', value=data['Delay'].values, dims='data')
idIdx = pm.ConstantData('idIdx', value=idx_i, dims='data')
### 事前分布
# α,β,γの正規分布パラメータ mu
# α,γは下限0・上限1の切断正規分布(TruncatedNormal)
muAlpha = pm.TruncatedNormal('muAlpha', mu=0.5, sigma=0.5, lower=0, upper=1)
muGamma = pm.TruncatedNormal('muGamma', mu=0.5, sigma=0.5, lower=0, upper=1)
# βは下限0の切断正規分布(TruncatedNormal)
muBeta = pm.TruncatedNormal('muBeta', mu=0, sigma=10, lower=0)
# α,β,γの正規分布パラメータ sigma
# 下限0のHalfStudentTで実装
sigmaAlpha = pm.HalfStudentT('sigmaAlpha', nu=3, sigma=1)
sigmaBeta = pm.HalfStudentT('sigmaBeta', nu=3, sigma=1)
sigmaGamma = pm.HalfStudentT('sigmaGamma', nu=3, sigma=1)
# α,β,γ
# α,γは下限0・上限1の切断正規分布(TruncatedNormal)
alpha = pm.TruncatedNormal('alpha', mu=muAlpha, sigma=sigmaAlpha,
lower=0, upper=1, dims='id')
gamma = pm.TruncatedNormal('gamma', mu=muGamma, sigma=sigmaGamma,
lower=0, upper=1, dims='id')
# βは下限0の切断正規分布(TruncatedNormal)
beta = pm.TruncatedNormal('beta',mu=muBeta, sigma=sigmaBeta, lower=0,
dims='id')
# 今日デートする魅力 U
U = pm.Deterministic('U', A, dims='data')
# 時間で変化する後日のデートの魅力 V
V = pm.Deterministic('V',
(alpha[idIdx] * pt.pow(gamma[idIdx], DELAY) * A
* (1 - pt.pow(gamma[idIdx], DELAY)) / (1 - gamma[idIdx])
+ A * pt.pow(gamma[idIdx], DELAY)),
dims='data')
# ソフトマックス行動選択を示すシグモイド関数 θ :範囲0~1
theta = pm.Deterministic('theta',
pm.invlogit(-beta[idIdx] * (U - V)),
dims='data')
### 尤度
likelohood = pm.Bernoulli('likelihood', p=theta, observed=C, dims='data')【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次を設定しました行の座標:名前「data」、値「行インデックス」
実験参加者IDの座標:名前「id」、値「idのラベル」
dataの定義
目的変数$${C}$$、説明変数$${A}$$(後日デートのモデルの好み度)、説明変数$${DELAY}$$(後日デートの遅延日数)、IDのインデックスを設定しました。パラメータの事前分布
モデルの数式表現のとおりに設定しました。alpha、beta、gammaの次元は「id」です。
U、V、thetaの次元は「data」です。
尤度
ベルヌーイ分布の確率パラメータpにtheta設定しました。
次元は「data」です。
2.モデルの外観の確認
### モデルの表示
model1【実行結果】

# モデルの可視化
pm.model_to_graphviz(model1)【実行結果】
大きなグラフになりました。
決定論的変数をすべてDeterministicで設定にしているからでしょう。

3.事後分布からのサンプリング
乱数生成数はテキストと変えています。
draws・tune・chainsの全てを増量しています。
また、後処理でWAICを計算するので、idata_kwargsで対数尤度を算出するように指定しています。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ2分20秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 2分20秒
# テキストはdraws=2000, tune=2000, thin=4, adapt_delta=0.9
with model1:
idata1 = pm.sample(draws=10000, tune=10000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=123,
idata_kwargs={"log_likelihood": True})【実行結果】省略

4.サンプリングデータの確認
InferenceDataに含まれる対数尤度データの様子を見てみましょう。
### idataの外観表示
idata1【実行結果】
「log_likelihood」グループが追加され、chain=4, draw=10000, data=720の形状で目的変数「likelihood」の対数尤度データが格納されています。

$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
rhat_idata1 = az.rhat(idata1)
(rhat_idata1 > 1.1).sum()【実行結果】
$${\hat{R} > 1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

パラメータ等の事後分布の要約統計量です。
### 推論データの要約統計情報の表示
var_names = ['muAlpha', 'muGamma', 'muBeta', 'sigmaAlpha', 'sigmaBeta', 'sigmaGamma']
pm.summary(idata1, hdi_prob=0.95, var_names=var_names)【実行結果】
テキストには事後分布の要約統計量が掲載されていないため、比較検証できませんでした。

トレースプロットを確認しましょう。
### トレースプロットの表示
pm.plot_trace(idata1, var_names=var_names, combined=True, figsize=(12, 15))
plt.tight_layout();【実行結果】
発散(divergences)のバーコードが見られます(エグいくらい)が、$${\hat{R}}$$より、収束していると考えましょう。

テキストにならって「WAIC」を確認しましょう。
pm.waic()の引数にlog_likelihoodを含んだidataを与えて実行します。
次のサイトを参考にして、scale引数にdevianceを設定しました。
arvizのWAICの使い方情報が少なくて困ります。。。
### WAICの計算
# elpd_waic:対数各点予測密度の期待値、p_waic:有効パラメータ数
# deviance:-2 * log-score
waic1 = pm.waic(idata1, scale='deviance')
print(waic1)【実行結果】
WAIC(debiance_waic)の値は$${869.2}$$です。
テキストの値:552.1よりも大きな値、つまり当てはまりが悪い結果になりました(泣)

【WAICとは?】
ベイズ推測のために、2009年に渡辺澄夫先生が公表した「広く使える情報量規準」(Widely applicable information criterion)です。
次のリンクで渡辺澄夫先生のサイトを参照できます。
5.分析~テキストにならって
制限付き総和型わくわく割引モデルによる選択確率のトレンドの描画
テキストの図6.4を代替します。
まずはデータの準備から。$${\theta_{data}}$$のデータ行単位の平均値を算出します。
### 描画データの準備
data2 = data.copy()
# thetaのデータ行単位の平均値を算出
data2['theta'] = idata1.posterior.theta.mean(('chain', 'draw')).data【実行結果】なし
続いて、個人ごとのグラフを描画します。
図6.4の左のグラフを代替します。
### 後日のデートの選択比率 ★図6.4に対応
# Cの平均、モデル1のthetaの平均を算出
ratio = data.groupby(['ID', 'Delay'])['C'].mean().reset_index()
ratio2 = data2.groupby(['ID', 'Delay'])['theta'].mean().reset_index()
# 描画
plt.figure(figsize=(6, 6))
# IDごとに描画処理を繰り返し実施
for i in sorted(ratio.ID.unique()):
# ID:iを取り出し
plot_tmp = ratio[ratio['ID']==i]
plot_tmp2 = ratio2[ratio2['ID']==i]
ax = plt.subplot(3, 3, i)
# Cの平均の折れ線グラフの描画
ax.plot(plot_tmp['Delay'], plot_tmp['C'])
# thetaの平均の折れ線グラフの描画
ax.plot(plot_tmp2['Delay'], plot_tmp2['theta'], '.--')
# 0.5の水平線の描画
ax.axhline(0.5, color='black', ls='--', lw=0.8)
# 修飾
ax.set_ylim(-0.1, 1.1)
ax.set_xticks([0, 10, 20, 30])
ax.set_title(f'ID:{i}')
if i==4:
ax.set_ylabel('遅延選択肢の選択比率(個人ごと)')
elif i==8:
ax.set_xlabel('デートまでの日数')
plt.tight_layout()
plt.show()【実行結果】
オレンジの点線が「後日のデートを選択する確率$${\theta_{data}}$$」の遅延日数別の推移です。
青い線は実験データの実績値です。
テキストと微妙に相違しますが、オレンジの推論は青い実績のトレンドを掴めているような感じがします。
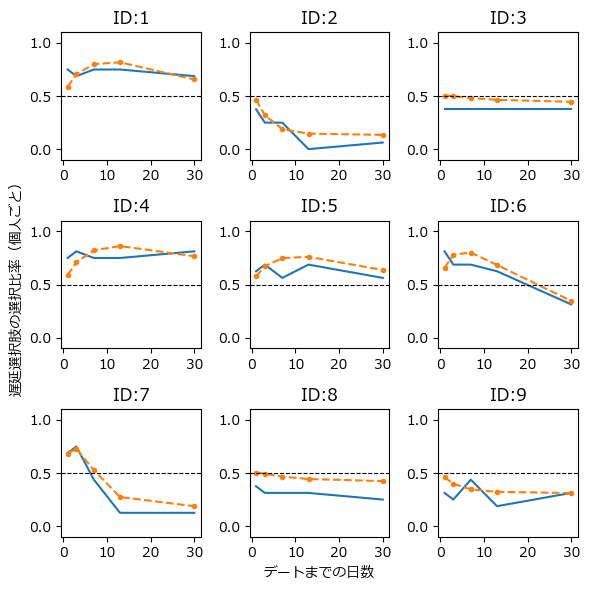
最後に全員の傾向を確認しましょう。
図6.4の右のグラフを代替します。
### 後日のデートの選択比率 ★図6.24に対応
# Cの平均、モデル1のthetaの平均を算出
ratio_all = data.groupby(['Delay'])['C'].mean().reset_index()
ratio_all2 = data2.groupby(['Delay'])['theta'].mean().reset_index()
# 描画
plt.figure(figsize=(4, 4))
# Cの平均の折れ線グラフの描画
plt.plot(ratio_all['Delay'], ratio_all['C'], label='data')
# thetaの平均の折れ線グラフの描画
plt.plot(ratio_all2['Delay'], ratio_all2['theta'], 's--', label=r'$\theta$')
# 0.5の水平線の描画
plt.axhline(0.5, color='black', ls='--', lw=0.8)
# 修飾
plt.title('後日のデートの選択比率(全体)')
plt.ylabel('遅延選択肢の選択比率(全体)')
plt.xlabel('デートまでの日数')
plt.legend()
plt.tight_layout()
plt.show()【実行結果】
テキストのトレンドよりも上側に0.05程度、過剰になっています(残念)。

【分析】
上のグラフが適切と仮定すると、3日後のデートを選択する確率が高いです(テキストも3日後)。
「選択確率の高い3日後を選んでデートに誘うと良い」とテキストでは(総和型わくわく割引モデルを)分析して締めくくっています。
遅くなりましたが、$${\theta_{data}}$$の事後分布の要約統計量とトレースプロットを確認します。
### thetaの事後分布の要約統計量
pm.summary(idata1, var_names=['theta'], hdi_prob=0.95)【実行結果】
一部のみの表示です。
HDI 2.5%~97.5%の範囲が広いものも含まれています。

トレースプロットです。
### thetaのトレースプロットの描画
pm.plot_trace(idata1, var_names=['theta'], compact=True, figsize=(12, 6));【実行結果】
0.5が突出した点になっているようです。

$${\theta_{data}}$$の事後分布からの全サンプリングデータでヒストグラムを描画してみましょう。
### thetaの事後分布のヒストグラム
plt.hist(idata1.posterior.theta.data.flatten(), bins=100, density=True);【実行結果】
0.5過剰、重心が右側(上側)に偏っている感じが見られます。
全ての遅延日数を含んでいるのでグラフの読み方には注意が必要です。

6.推論データ(idata)の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idataをpickleで保存します。
### idataの保存 pickle
file = r'idata1_ch06.pkl'
with open(file, 'wb') as f:
pickle.dump(idata1, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata1_ch06.pkl'
with open(file, 'rb') as f:
idata1_load = pickle.load(f)以上で第6章は終了です。
おわりに
「3日後のデートが最も魅力的」
考察と結論の項で執筆者は謹言しています。
乙女たちの素敵なデートが実現することを願って。
心理学っぽくて、ロマンがあって、信念に響く感じがして、ベイジアンの心も鷲掴みにするかもです!
ところで、この章で突如姿を現した「WAIC」。
WAICはある歌の記憶を呼び起こしてくれました。
きっとデートのわくわく気分を盛り上げてくれるでしょう。
グッドラック🤞
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析トピックを PythonとPyMC Ver.5で取り組みます。
豊富なテーマ(お題)を実践することによって、PythonとPyMCの基礎体力づくりにつながる、そう信じています。
日々、Web検索に勤しみ、時系列モデルの理解、Pythonパッケージの把握、R・Stanコードの翻訳に励んでいます!
このシリーズがPython時系列分析の入門者の参考になれば幸いです🍀
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
ベイズ書籍の実践記録も掲載中です。
最後までお読みいただきまして、ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
