
第5章「音声から感情はわかるか?」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング」の第5章「音声から感情はわかるか?」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
今回の章では、高さ・大きさ・長さなどの音声の物理的数値と感情表現の関連を乱塊計画モデルで分析しています。

今回もテキストの事後分布の要約統計量とほぼ同じ結果を実現できました!
さあ、PyMCでモデリングして、ベイズ推論を楽しみましょう!
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 鈴木朋子 先生
モデル難易度: ★★・・・ (やさしめ)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★★★・& ほぼ納得 \\
結果再現度 & ★★★★★& 最高✨ \\
楽しさ & ★★★★★ & 楽しい! \\
\end{array}
$$

評価ポイント
乱塊計画(乱塊法)のPyMCモデル表現に自信がない&もやもやしていて、難易度の星を1つ追加、実装精度の星を1つ減らしました。
もしや一般化線形モデル(GLM)の「formula形式」でモデル表記するのがよいかも?と考えて、PyMCの相棒「Bambi」を試しました🦌。
テキストの事後分布の要約統計量と概ね一致しているので良しとしましょう!

工夫・喜び・反省
テキストでは4つの音声物理量について1つづつ、感情との関連を分析していますが、この記事では「F0」(音声の高さ)の1つのみモデリングしました。主として時短目的です。
モデル内の観測データを差し替えれば他の3つの音声物理量のモデリングができると思います。
モデルの概要
テキストの調査・実験の概要
「ドラえもんはどうやってママの声から感情を推測できるのだろう?」
執筆者の調査動機がとても楽しいのです!

上図の「6つの感情x17名x4つの音声物理量」のデータをもとにして、音声物理量と感情の関連をベイズモデリングで探ります!
テキストのモデリング
■目的変数と関心のあるパラメータ
目的変数$${y_{jk}}$$は4つの音声物理量「F0」「F0レンジ」「音圧レベル」「発話時間」です。
関心のあるパラメータは乱塊計画の切片にあたる$${\alpha_j}$$です。
6つの感情表現を司るパラメータなのです!
添字$${j}$$は感情($${j=1, \cdots, 6}$$)、$${k}$$は発声者17($${k=1, \cdots, 17}$$)です。

■乱塊計画
音声物理量を目的変数(従属変数)、感情6水準を要因A、発声者を要因Bとする乱塊計画のモデルです。
$${\alpha_j}$$は要因A(感情)の固定効果、$${\beta_k}$$は要因B(発声者)の変量効果だそうです。
$$
\begin{align*}
y_{jk} &= \alpha_j + \beta_k + e_{jk} \\
e_{jk} &\sim \text{Normal}\ (0,\ \sigma_e) \\
\beta_k &\sim \text{Normal}\ (0,\ \sigma_{\beta})
\end{align*}
$$
上式を確率分布に紐つけると、次のようなStanスクリプト記述のモデルになります。
$$
\begin{align*}
y_{jk} &\sim \text{Normal}\ (\alpha_j + \beta_k,\ \sigma_e) \\
\beta_k &\sim \text{Normal}\ (0,\ \sigma_{\beta})
\end{align*}
$$
■パラメータの事前分布
パラメータの事前分布の記述は見当たりませんでした。

■分析・分析結果
PyMCのモデリング対象は「F0」(音声の高さ)といたします。
分析結果はテキストに記載のとおりです。
PyMCモデリングでの分析結果は、「PyMC実装」章の【分析】の部分をご覧ください。
PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.インポート
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')2.データの読み込み
csvファイルをpandasのデータフレームに読み込みます。
### データの読み込み
# データの読み込み
data = pd.read_csv('音声.csv')
# データの表示
display(data)【実行結果】
「F0」から「発話時間」が音声物理量であり、目的変数です。
「感情」は6つの感情のラベル、「emotion」は感情の名称です。
「発声者」は17名の発声者のラベルです。

3.データの外観・統計量
要約統計量を確認します。
### 要約統計量の表示
data.describe().round(2)【実行結果】

感情別の音声物理量のヒストグラムを確認しましょう。
### 感情ごとの音声物理量のヒストグラムの描画
plt.figure(figsize=(12, 15))
for i, emo in enumerate(data['emotion'].unique()):
for j, col in enumerate(data.columns[:4]):
plt.subplot(6, 4, i*4+j+1)
plt.hist(data[data['emotion']==emo][col], bins=8, edgecolor='white')
plt.title(f'{emo}:{col}')
plt.tight_layout()
plt.show()【実行結果】
感情によって音声物理量に特徴がありそうです。

感情ごとの音声物理量の箱ひげ図を描画します。
テキストの図5.1から図5.4を代替します。
### 感情ごとの音声物理量の箱ひげ図を描画 ★図5.1~5.4に対応
# ylabelの物理量の単位の設定
labels = ['(Hz)', '(Hz)', '', '(sec)']
# 描画
plt.figure(figsize=(8, 8))
# 4つ物理量ごとに箱ひげ図を描画
for i, (col, label) in enumerate(zip(data.columns[:4], labels)):
# 描画領域の確保
ax = plt.subplot(2,2,i+1)
# seabornのboxplotでemotion別の箱ひげ図を描画
sns.boxplot(data=data, x='emotion', y=col, fill=False, ax=ax)
# 修飾
ax.set_title(f'{col}(感情ごと)')
ax.set_xlabel('感情')
ax.set_ylabel(f'{col}{label}')
plt.tight_layout()
plt.show()【実行結果】
感情ごとに音声物理量の値が異なっている様子が確認できました。
F0(声の高さ)は感情による高低が顕著に表れている感じがします。


モデル1の実装
乱塊計画をPyMCの分布モデルに適切に落とし込みできているか、一抹の不安がありますが、ひとまず進めます。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
尤度$${likelihood}$$は正規分布を仮定しました。
パラメータ$${\alpha_j,\ \sigma_{\beta},\ \sigma_e}$$の事前分布には一様分布を仮定し、一様分布の範囲には$${100}$$を用いました
$$
\begin{align*}
\sigma_{\beta} &\sim \text{Uniform}(0,\ 100) \\
\sigma_e &\sim \text{Uniform}(0,\ 100) \\
\alpha_j &\sim \text{Uniform}(-100,\ 100) \\
\beta_k &\sim \text{Normal}(\text{mu}=0,\ \text{sigma}=\sigma_{\beta}) \\
likelihood &\sim \text{Normal}(\text{mu}=\alpha_j + \beta_k,\ \text{sigma}=\sigma_e) \\
\end{align*}
$$
1.モデルの定義
初期値、coord、data、パラメータの事前分布、尤度、計算値をそれぞれ指定します。
データの「感情」と「発声者」のラベルは0始まりになるようにデータ加工しました。
### モデルの定義
# 初期値設定:0始まりに変更
emo_idx = list(data['感情'].values - 1)
spe_idx = list(data['発声者'].values - 1)
# モデルの定義
with pm.Model() as model:
### データ関連定義
# coordの定義
model.add_coord('data', values=data.index, mutable=True)
model.add_coord('emotion', values=data['emotion'].unique(), mutable=True)
model.add_coord('speaker', values=data['発声者'].unique(), mutable=True)
# dataの定義
F0 = pm.ConstantData('F0', value=data['F0'], dims='data')
emotionIdx = pm.ConstantData('emotionIdx', value=emo_idx, dims='data')
speakerIdx = pm.ConstantData('speakerIdx', value=spe_idx, dims='data')
### 事前分布
# 事前分布
sigmaB = pm.Uniform('sigmaB', lower=0, upper=100)
sigmaE = pm.Uniform('sigmaE', lower=0, upper=100)
alpha = pm.Uniform('alpha', lower=-100, upper=100, dims='emotion')
beta = pm.Normal('beta', mu=0, sigma=sigmaB, dims='speaker')
### 尤度
likelihood = pm.Normal('likelihood', mu=alpha[emotionIdx] + beta[speakerIdx],
sigma=sigmaE, observed=F0,
dims='data')
### 計算値
# μ
mu = pm.Deterministic('mu', pt.mean(alpha, axis=-1))
# σ_α
sigmaA = pm.Deterministic('sigmaA', pt.std(alpha, axis=-1))
# η^2
eta2 = pm.Deterministic('eta2',
pt.pow(sigmaA, 2) / (pt.pow(sigmaA, 2) + pt.pow(sigmaE, 2)))
# δ
delta = pm.Deterministic('delta', sigmaA / sigmaE)
【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次を設定しました行の座標:名前「data」、値「行インデックス」
感情の座標:名前「emotion」、値「emotionの日本語ラベル」
発声者の座標:名前「speaker」、値「発声者のラベル」
dataの定義
目的変数$${y}$$、感情のインデックス、発声者のインデックスを設定しました。パラメータの事前分布
モデルの数式表現のとおりにsigmaB、sigmaE、alpha、betaを設定しました。
alpha の次元は「emotion」(感情)、betaの次元は「speaker」(発声者)です。尤度
正規分布の平均パラメータにalpha+betaを、標準偏差パラメータにsigmaEを設定しました。次元は「data」です。計算値
muは6つのalphaの平均値です。
pt.mean()はpytensor.tensorの平均計算関数です。sigmaAは6つのalphaの標準偏差です。
pt.std()はpytensor.tensorの標準偏差計算関数です。説明率eta2($${\eta^2}$$)は全分散(sigmaE²+simgaA²)に占めるalphaの分散sigmaA²の割合です。
pt.pow()はpytensor.tensorのべき乗計算関数です。効果量delta($${\delta}$$)はsigmaEに対するsigmaAの割合です。
2.モデルの外観の確認
# モデルの表示
model【実行結果】

# モデルの可視化
pm.model_to_graphviz(model)【実行結果】
計算値を含んでいるので複雑に見えますが、左の角丸四角の枠とalpha、beta&sigmaB、sigmaEに注目しましょう。

3.事後分布からのサンプリング
乱数生成数のうち、drawsとchainsはテキストどおり、tune(バーンイン期間)は10000に増量しました。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ30秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 30秒
with model:
idata = pm.sample(draws=20000, tune=10000, chains=5, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1234)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
rhat_idata = az.rhat(idata)
(rhat_idata > 1.1).sum()【実行結果】
$${\hat{R} > 1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

パラメータ等の事後分布の要約統計量です。
テキストの表5.1にならって、まず$${\alpha,\ \sigma_e,\ \sigma_{\beta},\ \mu, \sigma_{\alpha}}$$を表示します。
### 推論データの要約統計情報の表示 ★表5.1に対応
var_names = ['alpha', 'sigmaE', 'sigmaB', 'mu', 'sigmaA']
pm.summary(idata, hdi_prob=0.95, var_names=var_names).round(1)【実行結果】
EAP(mean)、post.sd(sd)、2.5%(hdi_2.5%)、97.5%(hdi_97.5%)の値はテキストとほぼ同じです!(やったー!)
なお、テキストの95%区間は信用区間ですが、summary関数の95%区間はHDI区間です。

続いて、$${\eta^2,\ \delta}$$です。
### 推論データの要約統計情報の表示 ★表5.1に対応
var_names2 = ['eta2', 'delta']
pm.summary(idata, hdi_prob=0.95, var_names=var_names2).round(3)【実行結果】
こちらもテキストとほぼ同じです。

トレースプロットを確認しましょう。
### トレースプロットの表示
var_names = ['alpha', 'sigmaE', 'sigmaB', 'mu', 'sigmaA', 'eta2', 'delta']
pm.plot_trace(idata, compact=False, combined=True, var_names=var_names,
figsize=(12, 20))
plt.tight_layout();【実行結果】
発散(divergences)のバーコードがちらほら見えますが、$${\hat{R}}$$より、収束していると考えましょう。

5.分析~テキストにならって
①F0のパラメータの事後分布の要約統計量
テキストの表5.1を代替します。
### F0の母数の事後分布の要約統計量 ★表5.1に対応
# 事後分布からのサンプリングデータより各パラメータの値を格納
a1 = idata.posterior.alpha[:, :, 0].data.flatten()
a2 = idata.posterior.alpha[:, :, 1].data.flatten()
a3 = idata.posterior.alpha[:, :, 2].data.flatten()
a4 = idata.posterior.alpha[:, :, 3].data.flatten()
a5 = idata.posterior.alpha[:, :, 4].data.flatten()
a6 = idata.posterior.alpha[:, :, 5].data.flatten()
sigma_e = idata.posterior.sigmaE.data.flatten()
sigma_b = idata.posterior.sigmaB.data.flatten()
mu = idata.posterior.mu.data.flatten()
sigma_a = idata.posterior.sigmaA.data.flatten()
eta_2 = idata.posterior.eta2.data.flatten()
delta_ = idata.posterior.delta.data.flatten()
# 要約統計情報を計算する関数の定義
def calc_stat(x):
return [np.mean(x), np.std(x), np.quantile(x, 0.025), np.median(x),
np.quantile(x, 0.975)]
# α、σ、μの表示
display(
pd.DataFrame({'α1_喜': calc_stat(a1),
'α2_悲': calc_stat(a2),
'α3_驚': calc_stat(a3),
'α4_恐': calc_stat(a4),
'α5_安': calc_stat(a5),
'α6_怒': calc_stat(a6),
'σe': calc_stat(sigma_e),
'σb': calc_stat(sigma_b),
'μ': calc_stat(mu),
'σa': calc_stat(sigma_a)},
index=['EAP', 'post.sd', '0.025', 'MED', '0.975']
).T.round(1))
# η²、δの表示
display(
pd.DataFrame({'η^2': calc_stat(eta_2),
'δ': calc_stat(delta_)},
index=['EAP', 'post.sd', '0.025', 'MED', '0.975']
).T.round(3))【実行結果】
先にみた要約統計量とややズレています。
発散(divergences)したデータを含めて計算したからでしょうか・・・。

【分析】
説明率$${\eta^2=44\%}$$、効果量$${\delta=0.88}$$倍の値はともに「大きい」そうです。
$${\alpha}$$については、驚きが最も大きい=声が高い、悲しいが最も小さい=声が低いとなっています。
$${\alpha}$$の大きい=声が高い順に並べると、
驚き > 喜び > 怒り > 恐れ > 安心 > 悲しみ
となりました。

②感情間の大小の確率を確認
事後分布からのサンプリング100000個を大小比較します。
テキストの表5.2を代替します。
### F0の切片に対して感情i行がj行より大きい確率の算出 ★表5.2に対応
# 初期値設定
data_list = [a1, a2, a3, a4, a5, a6] # 事後分布
name_list = ['α1_喜', 'α2_悲', 'α3_驚', 'α4_恐', 'α5_安', 'α6_怒'] # 項目名
compare_prob = np.zeros((len(data_list), len(data_list))) # 一時配列
# 切片αについてi行>j行の確率の計算
for i, a_i in enumerate(data_list):
for j, a_j in enumerate(data_list):
compare_prob[i, j] = sum(a_i > a_j) / a_i.size
# 表示
pd.DataFrame(compare_prob, index=name_list, columns=name_list).round(1)【実行結果】
数値は行の感情が列の感情よりも値が大きい確率を示しています。
テキストと一致しています。

【分析】
「驚き」は他のすべて感情よりも値が大きい=音声が高いようです。
「悲しみ」は他のすべて感情よりも値が小さい=音声が低いようです。
「恐れ」は「安心」よりも音声が高い割合が90%です。
「喜び」は「怒り」よりも音声が高い割合が70%です。

6.推論データ(idata)の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idataをpickleで保存します。
### idataの保存 pickle
file = r'idata_ch05.pkl'
with open(file, 'wb') as f:
pickle.dump(idata, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata_ch05.pkl'
with open(file, 'rb') as f:
idata_load = pickle.load(f)
Bambiで実装
乱塊計画等の一般化線形モデルで表現された数式は「formula構文」を用いる方がモデル化しやすいかもしれません。
PyMC Ver.5 では、Bambiパッケージで「formula構文」のモデリングを行います。
Bambiは「BAyesian Model-Building Interface」の略です。
子鹿のバンビでは無いと思います・・・

モデルの数式表現
モデル1と同じモデルを目指してみます。
1.インポートとモデルの定義
### インポート
import bambi as bmb事前分布とモデルを定義します。
計算値$${\mu,\ \sigma_{\alpha},\ \eta^2,\ \delta}$$は省略します。
定義の仕方が分かりません(汗)
### モデルの定義 by bambi
# 事前分布の定義
priors = {'sigma': bmb.Prior('Uniform', lower=0, upper=100),
'1|発声者': bmb.Prior('Normal', mu=0,
sigma=bmb.Prior('Uniform', lower=0, upper=100)),
}
# formulaを使ったモデルの定義
model_bmb = bmb.Model(formula='F0 ~ 0 + emotion + (1|発声者)', data=data,
categorical=['emotion', '発声者'], priors=priors)【モデル注釈】
事前分布
辞書形式でパラメータの事前分布bmb.Priorを記述します。sigma
$${\sigma_e}$$です。モデルの標準偏差になります。
事前分布Priorは$${\text{Uniform}\ (0,\ 100)}$$です。1|発声者
$${\beta_k}$$です。
事前分布Priorは$${\text{Normal}\ (0,\ \sigma_{\beta})}$$です。
1は切片です。切片を指定しないと$${\beta_k}$$の分布を指定できなかった(やり方が他に分からなかった)ので、入れました。
$${\sigma_{\beta}}$$の事前分布Priorは$${\text{Uniform}\ (0,\ 100)}$$です。
formulaを用いたモデルは次のように実装しました。
formula : F0 ~ 0 + emotion + (1 | 発声者)
目的変数はF0、0は切片なしの宣言、説明変数はemotionと(1 | 発声者)です。交互作用項はありません。categoricalでemotionと発声者をカテゴリ変数に指定します。
priorに事前分布を設定した辞書priorsを指定します。
2.モデルの外観の確認
モデル式を見てみましょう。
# モデルの表示
model_bmb【実行結果】
Bambiによって解釈されたモデルの全貌です。
モデルは gaussian:正規分布であり、パラメータ$${\mu}$$はemotionの効果と(1 | 発声者)の効果があること、emotionに正規分布が仮定されていることなどが分かります。

モデルのグラフ表現を確認します。
モデルのbuild後、または、fit後に可視化可能になります。
# モデルの可視化
model_bmb.build()
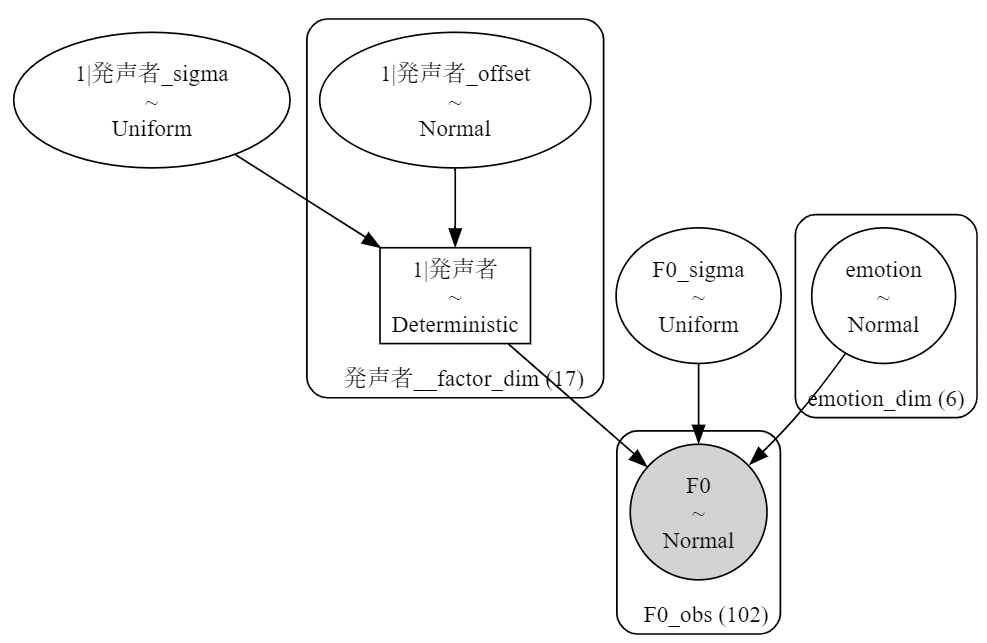
model_bmb.graph()【実行結果】
計算値を定義していないのでサッパリした構成です。
変数「emotion」自体、および、変数「発声者」(たぶん)に正規分布が仮定されています。
3.事後分布からのサンプリング
fitメソッドを利用して事後分布からのサンプリングを行います。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ20秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 20秒
idata_bmb = model_bmb.fit(draws=20000, tune=10000, chains=5, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1234)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
rhat_idata_bmb = az.rhat(idata_bmb)
(rhat_idata_bmb > 1.1).sum()【実行結果】
$${\hat{R} > 1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

事後分布の要約統計量を確認しましょう。
### 推論データの要約統計情報の表示
var_names=['emotion', 'F0_sigma', '1|発声者_sigma']
pm.summary(idata_bmb, hdi_prob=0.95, var_names=var_names).round(1)【実行結果】
emotionはテキストの$${\alpha}$$に、F0_sigmaはテキストの$${\sigma_e}$$にそれぞれ相当し、(1|発声者)はテキストの$${\sigma_{\beta}}$$に(たぶん)近似するものです。
テキストとほぼ同じ値になりました。

トレースプロットを確認しましょう。
### トレースプロットの表示
pm.plot_trace(idata_bmb, var_names=var_names, compact=False, combined=True,
figsize=(12, 20))
plt.tight_layout();【実行結果】
発散のバーコードは無く、グラフの様子から収束していることが想像できます。

5.分析~テキストにならって
F0のパラメータの事後分布の要約統計量を表示しましょう。
テキストの表5.1を代替します。
### F0の母数の事後分布の要約統計量 ★表5.1に対応(ただしη^2,δは省略)
a1 = idata_bmb.posterior.emotion[:, :, 0].data.flatten()
a2 = idata_bmb.posterior.emotion[:, :, 1].data.flatten()
a3 = idata_bmb.posterior.emotion[:, :, 2].data.flatten()
a4 = idata_bmb.posterior.emotion[:, :, 3].data.flatten()
a5 = idata_bmb.posterior.emotion[:, :, 4].data.flatten()
a6 = idata_bmb.posterior.emotion[:, :, 5].data.flatten()
sigma_e = idata_bmb.posterior.F0_sigma.data.flatten()
sigma_b = idata_bmb.posterior['1|発声者_sigma'].data.flatten()
# 要約統計情報を計算する関数の定義
def calc_stat(x):
return [np.mean(x), np.std(x), np.quantile(x, 0.025), np.median(x),
np.quantile(x, 0.975)]
pd.DataFrame({'α1_喜': calc_stat(a1),
'α2_悲': calc_stat(a2),
'α3_驚': calc_stat(a3),
'α4_恐': calc_stat(a4),
'α5_安': calc_stat(a5),
'α6_怒': calc_stat(a6),
'σe': calc_stat(sigma_e),
'σb': calc_stat(sigma_b)},
index=['EAP', 'post.sd', '0.025', 'MED', '0.975']
).T.round(1)【実行結果】
テキストの表5.1とだいたい一致しています。

続いて要約推定量を表示します。テキストの表4.3を代替します。
### パラメータの事後分布の要約統計量 ★表4.3に対応(ただしMAPは省略)
# 要約統計情報を計算する関数の定義
def calc_stat(x):
return [np.mean(x), np.std(x), np.quantile(x, 0.025), np.median(x),
np.quantile(x, 0.975)]
pd.DataFrame({'π': calc_stat(pi_data),
'θ1': calc_stat(theta1_data),
'θ2': calc_stat(theta2_data)},
index=['EAP', 'post.sd', '0.025', 'MED', '0.975']
).T.round(3)【実行結果】
テキストの統計値とおおむね一致しています。
表5.2の確率も確認しましょう。
### F0の切片に対して感情i行がj行より大きい確率の算出 ★表5.2に対応
# 初期値設定
data_list = [a1, a2, a3, a4, a5, a6] # 事後分布
name_list = ['α1_喜', 'α2_悲', 'α3_驚', 'α4_恐', 'α5_安', 'α6_怒'] # 項目名
compare_prob = np.zeros((len(data_list), len(data_list))) # 一時配列
# 切片αについてi行>j行の確率の計算
for i, a_i in enumerate(data_list):
for j, a_j in enumerate(data_list):
compare_prob[i, j] = sum(a_i > a_j) / a_i.size
# 表示
pd.DataFrame(compare_prob, index=name_list, columns=name_list).round(1)【実行結果】
テキストの表5.2とピッタリ一致しました。


6.推論データ(idata)の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idata_bmbをpickleで保存します。
### idataの保存 pickle
file = r'idata_bmb_ch05.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_bmb, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata_bmb_ch05.pkl'
with open(file, 'rb') as f:
idata_bmb_load = pickle.load(f)以上で第5章は終了です。
おわりに
オチはのび太くんのママの登場
ドラえもんのオチはのび太のママの怒鳴り声だけど、ロボットのドラえもんはどうやってママの声から感情を推測するのだろう。
執筆者はさらに疑問を繋げて、機械との楽しい会話を目指そう、という新たな視点を生み出しています。すごい!

テキストには、F0:音声の高さ、F0レンジ:音声の抑揚、音圧レベル:音声の大きさ、発話時間の4つの音声物理量について、感情によってどのような差異を生み出されるのかを分析しています。
ぜひテキストをお読み下さい。
キーワードは「データを比較する、差を分析する」です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析トピックを PythonとPyMC Ver.5で取り組みます。
豊富なテーマ(お題)を実践することによって、PythonとPyMCの基礎体力づくりにつながる、そう信じています。
日々、Web検索に勤しみ、時系列モデルの理解、Pythonパッケージの把握、R・Stanコードの翻訳に励んでいます!
このシリーズがPython時系列分析の入門者の参考になれば幸いです🍀
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
ベイズ書籍の実践記録も掲載中です。
最後までお読みいただきまして、ありがとうございました。
