
New Method to Solving the Collatz Conjecture 1 with High-Prize Money
Link
Summary Video of the New Method in English
The new method is introduced in Articles 1-10 and Chapters 1-8.
The translation from Japanese to English has been completed for all articles, both free and paid. (April 2024)
English articles are marked as (E) in the following linked list.
(The mark (E) will be retained.)
There are six paid sections in total, marked as (p) in the following linked list.
The free article mainly provides a qualitative explanation of the new method. The outline of the new method can be grasped even with only the free chapters and sections. The paid article mainly provides a quantitative explanation.
When translating from Japanese to English, subtle nuances of the original articles may not be fully conveyed. If you would like to view the original Japanese articles, please see Chapter 1 of Japanese Article 1.
Chapter 2: Derivation of CS-Vibration and CS-Plot (article 2) (E)
2.1 What is CS-Vibration
2.2 Derivation Formula of CS-Vibration and CS-Plot (p),
Chapter 2: Derivation of CS-Vibration and CS-Plot (article 3) (E)
2.3 Relationship between the Derivation of the CS-linear-equations and CS-Plot Points
2.3.1 Before Explanation
2.3.2 Preparation for Derivation (p),
2.3.3 Specific Example (p),
2.3.4 Relationship between the Derivation of the CS-linear-equations and
CS-Plot Points (p),
Chapter 3: Classification of Odd Numbers (article 4) (E)
3.1 Classification of Odd Numbers (Nc and Ns Types)
3.2 Characteristics of Nc and Ns Types
Chapter 4: Relationship between Odd Number Classification
and S-Transformation (article 5) (E)
4.1 Summary of Previous Chapters
4.2 Definition and Specific Example of S-Transformation (p),
4.3 Derivation of S-Transformation (p),
4.4 Characteristics of S-Transformation (p),
Chapter 5: Chaos Dynamics 1D Mapping (article 6) (E)
5.1 Similarity between the Collatz Conjecture (CS-Space)
and 1D Mapping
5.2 Tent Map (Example of 1D Mapping)
change of pace: Monster Hunter
Chapter 6: Propositions on CS-Space Equivalent to the Collatz Conjecture (article 7) (E)
6.1 Proposition on CS-Space Equivalent to the Collatz Conjecture
(Weak Proposition)
Chapter 6: Propositions on CS-Space Equivalent to the Collatz Conjecture (article 8) (E)
6.2 Proposition on CS-Space Equivalent to the Collatz Conjecture
(Strong Proposition)
6.2.1 Weak propositions are parasites of their parents, but their growth
far exceeds that of their parents.
6.2.2 Strong propositions are independent of their parents and grow
even larger.
6.2.3 CS-alternating transformation plot
6.2.4 Strong proposition on CS-space equivalent to the Collatz
conjecture
6.2.5 Quantitative additional explanation for Section 6.2 (p)
Chapter 7: Can the Collatz Conjecture be Solved? Maybe? Possibly? (article 9) (E)
7.1 Difficult to Solve out using Conventional Methods
7.2 Bernoulli Shift (Binary Transformation) Mapping
7.3 Towards Elucidation and a New Field
Chapter 8: Encounter (article 10) (E)
8.1 Encounter
8.2 Other Unsolved Prize Problems That Seem Challenging
Chapter 1: Introduction to a New Method (article 1)
1.1 The Collatz Conjecture: A Famous Unsolved Problem
The Collatz conjecture is a famous unsolved problem in mathematics.
Despite its simple rules, it has remained unsolved for over 80 years.
A Japanese company has offered a prize of 120 million yen for its solution.
For those who are new to the Collatz conjecture and are visiting this site for the first time, I will explain the conjecture in a way that can be understood with high school math, and introduce a new approach (a new way of looking at it) to solving it.
The Collatz conjecture states that for any positive integer, if you repeatedly apply the following rules, the sequence will eventually reach 1:
・If the number is odd, triple it and add 1.
・If the number is even, divide it by 2.
Let's take 13 as an example.
Since 13 is odd, we triple it and add 1 to get 40.
40 is even, so we divide it by 2 repeatedly 3 times to get 5.
5 is odd, so we triple it and add 1 to get 16.
16 is even, so we divide it by 2 repeatedly 4 times to get 1.
$${13 \to 40 \to 20 \to 10 \to 5 \to 16 \to 8 \to 4 \to 2 \to 1}$$
Additionally, 1 is the only number that loops, following the sequence:
$${1 \to 4 \to 2 \to 1}$$
So far, it has been verified that all positive integers up to $${2^{68}}$$ eventually reach 1 when the Collatz rules are repeatedly applied. This means that for all numbers less than or equal to $${2^{68}}$$, excluding 1, the sequence will never return to the same number (i.e., it will not loop) and will never increase indefinitely.
1.2 Has the Collatz Conjecture Been Solved?
In September 2019, Terence Tao, a world-renowned mathematician and Fields Medalist, published a pre-print on arXiv (a repository for open access scientific papers) that made significant progress towards solving the Collatz Conjecture. The paper, which was later published in May 2022, showed that the conjecture is "almost always" true for almost all positive integers.
However, Tao himself acknowledged that a complete proof of the conjecture is still out of reach. His work provides strong evidence in support of the conjecture, but it does not definitively establish its validity.
Additional Information:
Terence Tao's arXiv pre-print: https://www.math.ucla.edu/~tao/preprints/
Terence Tao's published paper: https://scholar.google.com/citations?user=TFx_gLQAAAAJ&hl=en
To prove the Collatz Conjecture, two key points need to be established:
1. Boundedness: For all positive integers, the Collatz sequence will not increase indefinitely. In other words, there exists a maximum value for the sequence, and it will not reach an infinite number of steps.
2. Non-recurrence: For all positive integers except 1, the Collatz sequence will never return to the same number. In other words, the sequence will not loop.
If these two points can be proven, it follows that the sequence will eventually reach 1 after a finite number of steps for any positive integer.
The finite number of steps is also one of the conditions.
To prove the Collatz Conjecture, it is not enough to show that:
The sequence converges to 1: It is not sufficient to simply demonstrate that the sequence reaches 1 after an infinite number of steps.
The sequence reaches 1 for specific positive integers: Proving that the sequence reaches 1 for a particular set of positive integers, even if a pattern is observed, is not enough. The observed pattern must be generalizable to all positive integers. This is a common misconception found online.
On the other hand, to disprove the Collatz Conjecture, it suffices to find a single positive integer for which the sequence does not reach 1. The existence of a single counterexample would invalidate the conjecture.
1.3 Famous Amateur Mathematicians
Throughout history, many individuals have made significant contributions to mathematics, even without being professional mathematicians. These amateur mathematicians have solved challenging problems and left their mark on the field.
Pierre de Fermat:
Famous for Fermat's Last Theorem, which remained unproven for over 350 years.
Worked as a lawyer in France and pursued mathematics as a hobby.
Also known as the "Father of Number Theory" and made many important contributions to mathematics.
Alfred Kempe:
Co-discoverer of the four color theorem, a fundamental problem in graph theory.
Worked as a barrister in London and was an amateur mathematician.
His solution to the four color theorem was later found to be incomplete, but it was proved that five colors are sufficient to color a map using the logic used in Kemp's proof (five color theorem).
Évariste Galois:
French mathematician who made fundamental contributions to group theory and Galois theory, which are essential in modern mathematics.
These are just a few examples of the many amateur mathematicians who have made significant contributions to the field. Their work demonstrates that mathematical talent and creativity can be found in people from all walks of life, and that passion and dedication can lead to groundbreaking discoveries.
The Openness of Mathematical Discovery
The examples of famous amateur mathematicians demonstrate that solving challenging mathematical problems is not limited to professionally trained mathematicians. Ordinary people with a passion for mathematics can also make significant contributions.
The story of George Dantzig, a graduate student who solved an unsolved problem in statistics on a chalkboard, mistakenly thinking it was a homework assignment, is a testament to this openness. His story even inspired a movie.
It is impossible to predict when, where, or by whom an unsolved problem will be solved. It may be by a professional mathematician working in a university, or it may be by an amateur with a natural talent and a deep passion for the subject.
This unpredictability is part of what makes mathematics so exciting and captivating. There is always the possibility that someone, somewhere, is on the verge of making a groundbreaking discovery that will change the way we understand the world.
1.4 More Lasting Legacy Than the Nobel Prize?
The Nobel Prize is awarded annually in various fields, including physics, chemistry, and medicine. Up to three individuals can be awarded for the same theme in each field. The prize undoubtedly leaves its mark on history.
Over 100 years, 300 people are recognized in each field, and over 600 over 200 years.
However, even for great people, it seems that their names fade away when their numbers reach 300 or 600.
On the other hand, only a handful of individuals have been able to solve major unsolved problems in the history of mathematics, such as Andrew Wiles, who solved Fermat's Last Theorem, and Grigori Perelman, who solved the Poincaré Conjecture.
Solving other unsolved problems before the age of 40 may also lead to the Fields Medal, which is known as the Nobel Prize of mathematics.
Personally, I believe that the latter is more likely to leave a lasting legacy.
1.5 Is Mathematics an Invention or a Discovery?
Knot theory is a branch of mathematics that studies the classification and properties of knots based on their topological features. it may seem like an abstract and esoteric field at first glance.
However, it was discovered that this theory was related to the laws of the universe. knot theory has surprisingly broad and diverse applications in various scientific and technological fields.
Is mathematics an "invention" or is it something that existed in the universe independently of humanity, and we simply "discovered" it?
It is undeniable that the truth of the Collatz conjecture may simply be something that humanity does not yet know. This is not limited to the Collatz conjecture; it is a deeply moving sentiment.
1.6 Even in the process of solving
In many scientific fields other than mathematics, experiments are often required for verification, which can be expensive. In contrast, in mathematics, all you need to verify a proof is a single computer for analysis. You can do it at home without having to worry about the world or other people's opinions.
when you solve a problem, glory awaits you.
There are several unsolved problems in the history of mathematics (some with million-dollar prizes), but I think the Collatz conjecture is the most accessible one.
If you enjoy solving puzzles or entrance exams, why not give it a try?
Life is a one-time experience for everyone.
The process of solving can also lead to various byproducts.
Yuri Matiyasevich produced a formula that generates primes from
a 19-variable polynomial as a byproduct of solving Hilbert's tenth problem.
Sophie Germain, a French female mathematician, proved that Fermat's Last Theorem is true for odd primes.
At that time, women were not allowed to become mathematicians, so she corresponded with Gauss and Legendre under the male pseudonym "Le Blanc." Gauss, highly impressed by her work, awarded her an honorary doctorate from the University of Göttingen.
Her pioneering proof made her name in history.
When it comes to prime numbers, the pinnacle of integer theory, and of mathematics itself, "What is the rule for the arrangement of prime numbers?",
a law that even elementary school students can understand the meaning of the problem, has not yet been found.
Many great mathematicians have left behind many theorems and theories in the process of solving it. There is also a mathematical dictionary of prime numbers.
1.7 Solving and Challenging in a Different Field
By solving a problem in one field with another field, the latter field can also be developed.
While Euclid's proof of the infinitude of primes dates back to ancient Greece, Euler's proof, though considerably more complex, marked the beginning of analytic number theory (number theory using calculus) by incorporating series and other concepts from analysis.
Grigori Perelman solved the Poincaré conjecture, a famous mathematical problem, using methods from physics rather than mathematics. He also declined the Fields Medal, considered the Nobel Prize of mathematics, and a $1 million prize.
Isn't he incredibly cool?
The Collatz conjecture may also lead to new discoveries in other fields by challenging it from a different perspective. The new method for solving the Collatz conjecture was discovered while challenging it from a different field (mathematics).
It would be really cool if you could challenge the Collatz conjecture from a physics perspective.
It would raise profound questions about the nature of mathematics itself: is it an invention or a discovery?
1.8 Creator's Introduction
Since the background of the creator is completely unknown, it may affect the credibility of the article. Therefore, I would like to briefly introduce myself.
I graduated from the University of Tokyo and received a Ph.D. in Physics from the same university. My specialization is optical physics, and I have worked as an engineer at Fujitsu Laboratories and other manufacturers, where I have experience in both experimental and theoretical work. My main areas of theoretical analysis are crystal oscillators and photonic crystals.
By chance, I came across a book on number theory and became fascinated by the field. In particular, I was drawn to the Collatz conjecture, a famous unsolved problem with a long history. I had also read several books on other fields completely unrelated to number theory, and I wondered if I could apply the knowledge I gained from them to the analysis of the Collatz conjecture.
Furthermore, I discovered a proposition in an entirely different field that is equivalent to the definition of the Collatz conjecture.
While the goal differs from that of the Riemann hypothesis,
all sequences of numbers that follow the Collatz rule, regardless of their initial value, lie on a CS straight line in CS space.
This finding should be of great interest to those already working on the Collatz conjecture, as it offers a perspective from a different field.
1.9 Before Explaining the New Method
Regarding the Collatz conjecture rule:
For odd numbers, triple the number and add 1.
For even numbers, divide the number by 2.
Since any even number will eventually reach an odd number through repeated division by 2, Only odd numbers will be tracked, while even numbers will be omitted unless specifically mentioned.
For example, in the case of 13 from Section 1.1, Only the odd numbers will be shown: $${13 \to 5 \to 1}$$
The total number of steps until reaching 1 is the total number of $${\to}$$, which in the case of 13 is 2.
Let $${No}$$ be an odd integer. Although $${No=27}$$ is a small number, it has a total of 41 steps as shown below. Only odd numbers are tracked and the maximum number is 3077.

Figure 1-2 shows the odd number changes on the horizontal axis
(step number 0 for 27, step number 41 for 1) and the odd number values for each number on the vertical axis.
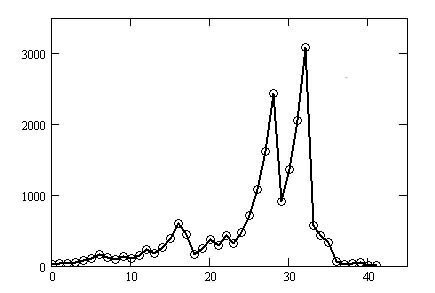
When the graph in Figure 1-2 is transformed using the new method, the result is Figure 1-3.
I will call this the CS-vibration, where C also refers to the C of the Collatz conjecture.
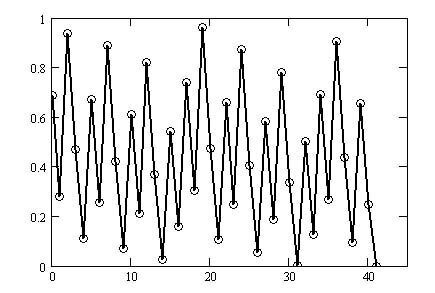
Figure 1-3 shows more regularity and periodicity than Figure 1-2.
This regularity is just the beginning, and I will apply several more transformations. This will reveal even clearer regularity. The same tendency appears for initial values other than 27, albeit with a difference in the number of steps.
Finally, I will present a general formula and proposition that explain this tendency for any odd integer $${No}$$.
Variables and Definitions:
$${N}$$、$${No}$$、
total number of steps, step number, CS-vibration
Chapter 1 provides an introduction to various topics before the analysis using the new method. If you find the content of this article to be insightful, please rate it highly. This will encourage me to continue my analysis in the future.
Please also check out the Iroha Uta song in "change of pace".
1-10. About the articles in Chapter 2 and beyond
The articles on the new method are from Chapter 1 (Article 1) to Chapter 8 (Article 10), and Chapter 6.1 (Article 7) and 6.2 (Article 8) are the main articles on the analysis of the new method. The weak proposition and strong propositions in Chapter 6 can be understood from the terms, variables, and derived formulas introduced in Chapters 2 to 5.
By explaining the content in the form of an article, it becomes more readable and I can include many examples, which makes it easier to understand. In contrast, a paper condenses the content and requires attention to the format, which can take time to understand.
Please grasp the essential parts and use them as hints for the analysis of the Collatz conjecture.
In each chapter, key content is made available as a paid article. In some cases, even sections within a chapter may be paid articles, even if they are not key content. In the latter case, but not always, this includes the derivation and proof of formulas.
The next article is Chapter 2 (2.1 & 2.2).
Section 2.2 is a paid article, as it covers the derivation method of CS- vibration and the introduction of further transformation of CS-vibration in general odd numbers $${\bm{No}}$$, with an explanation of transformation characteristics using $${\bm{No=27}}$$ as an example.
The summary video linked at the beginning, as well as the free articles and the articles with a paywall, will be very helpful in making your decision.
change of pace: Creative Iroha Uta
I would like to widely share the following Iroha Uta:
(1) Mt.Fuji Iroha Uta in 7-5-7 rhythm
(2) VICTORY Iroha Uta
For those who wish to purchase the set of 8 postcards of Mt. Fuji Iroha Uta, there is a small "Contact the Creator" 「クリエータへのお問い合わせ」link at the very end of the article. Clicking on this link will allow you to send a message to the creator with your order details.
A1. Postcard Sample Images




A2. About Modern Iroha Uta
Tanka and Haiku are traditional Japanese poems that have been around for centuries.
Tanka consists of 31 syllables in a 5-7-5-7-7 pattern.
Haiku consists of 17 syllables in a 5-7-5 pattern.
Both tanka and haiku are popular among the general public and are often published in newspapers. In fact, the present day is even said to be a tanka boom.
The Iroha Uta is a traditional Japanese poem that uses all 46 characters of the Japanese syllabary in alphabetical order. The original Iroha Uta, which begins with "iroha nihoheto," 「いろはにほへと」uses the old kana system and has a history of over 1000 years. It is a respected poem due to its long history and strict rules.
Modern Iroha Uta has not become widely popular due to its strict rules.
Even though many people are familiar with the original Iroha Uta, they are often not aware of its rules.
The rules for composing an Iroha Uta are as follows:
Use all 46 characters of the Japanese hiragana syllabary.
Each character can only be used once.
The modern hiragana syllabary consists of 46 characters, from "あ" to "ん".
In other words, if you write an Iroha Uta using only hiragana and check each character in order from "あ" to "ん", you will end up with "ん".
A3: The 7-5 Syllable Fujiyama Iroha Uta(Figure a1, Figure a2)
The 7-5 Syllable Fujiyama Iroha Uta is a poem composed by my late father when he was still in good health. It was serialized in the Nihon Keizai Shimbun (Nikkei), a famous Japanese newspaper, and the monthly magazines of a famous Japanese educational publisher, Obunsha, at the time. It was also introduced on TV and other media.
The creator of the poem has stated in the Nihon Keizai Shimbun that
"a scientific mind is also necessary for creation."
Indeed, since the poem is created by rearranging the 46 characters of the Japanese hiragana syllabary, it also has a puzzle-like element. The difficulty of creation is much higher than that of tanka or haiku.
The 7-5 Syllable Mt.Fuji Iroha Uta is a poem that follows the rules of the Iroha Uta. Furthermore, it also follows the rules of tanka and haiku: It is written in the 7-5 syllable meter, which is a traditional Japanese poetic meter.
This makes the poem very difficult to create, and it is something that cannot be easily imitated. The content of the poem is also very beautiful.
I have combined the 7-5 Syllable Mt.fuji Iroha Uta with photos and paintings of Mt. Fuji to create postcards.


A4: The VICTORY Iroha Uta (Figure a3, Figure a4)
The VICTORY Iroha Uta is a poem that is common to all those who wish for victory. It is combined with the most famous Mt. Fuji ukiyo-e of the famous Japanese ukiyo-e artist, Katsushika Hokusai.
この記事が気に入ったらサポートをしてみませんか?
