コラッツ予想解明への新解析手法の紹介7ー 問題の意味が小学生でもわかる数学の高額懸賞金歴史的未解決問題
第6章 コラッツ予想と同値なCS空間上の命題
今回の記事(7回目)をご覧になる前に「第1章 新手法の紹介の前に」をご覧ください。
また第1章には各章へのリンクが貼ってあります。
6.1 コラッツ予想と同値なCS空間上の命題(弱い命題)
第2,3,4,5章で「コラッツ予想と同値なCS空間上の命題」を理解するための土台は全て説明しました。この章では今までに示した図、グラフ、数式を主として解説し、解説に必要なグラフは追加して、最後に同値な命題(弱い命題)を紹介します。
第5章で紹介したローレンツプロットは一見ランダムに見えるシグナルから規則性を見出す手法です。かなり強力です。
6.1.1 2種ローレンツプロットの比較
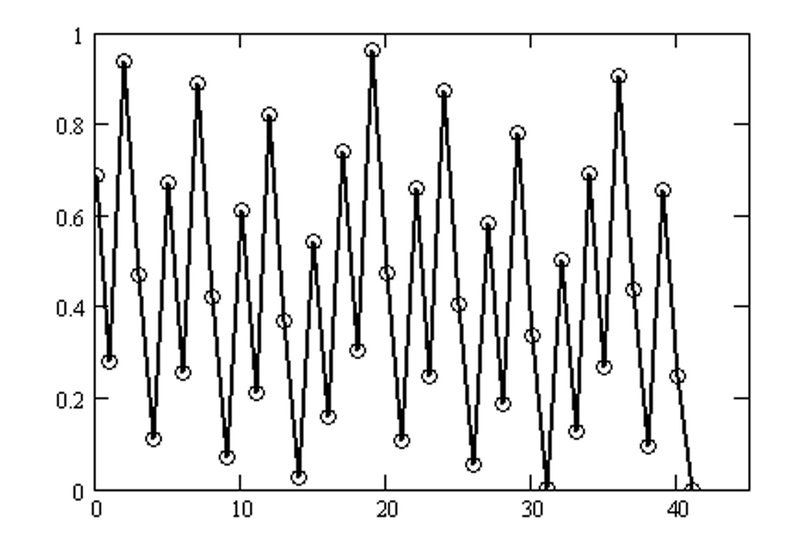
図6-1は第2章でも記載した初期値27が1に到達するまでの奇数のみ表示したステップ図(上)とその経過グラフです(下)。42点あります。
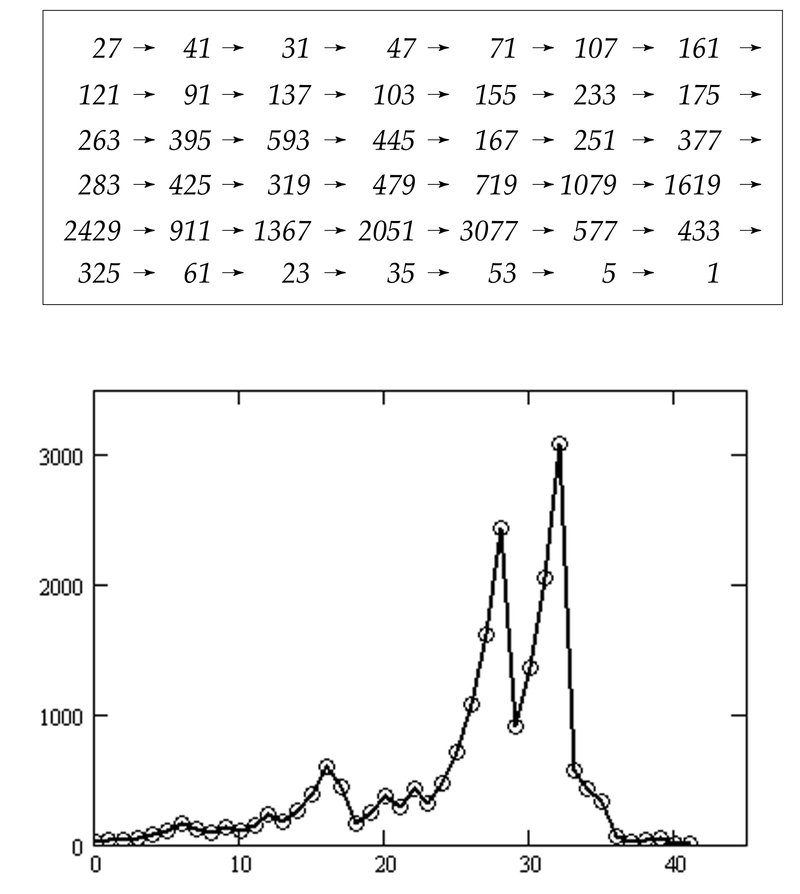
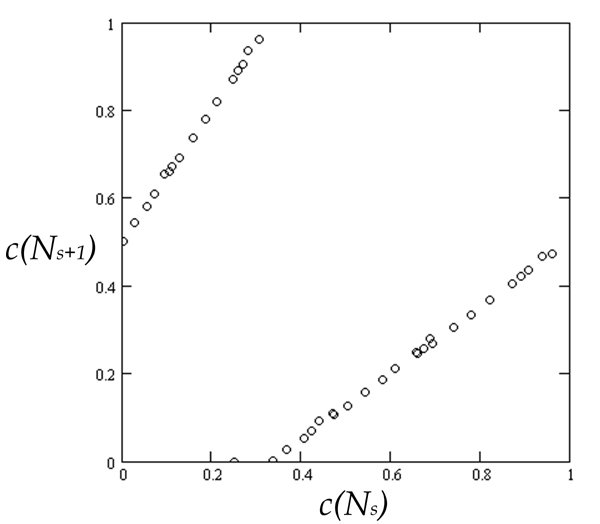
図6-1のグラフを見ても規則性は見られませんが、試しにこれをローレンツプロットしてみます。図6-2左図に示しました。プロット点は$${(27,41), (41,31), (31,47), \cdots ,(35,53), (53,5), (5,1)}$$の41個です。何かしらの規則性が現れましたね。直線で近似できそうなプロット点が2,3本見えています。右図は全てのプロット点を最大値3077で割って0以上1以下に収まるようにしたローレンツプロットで、左図と当然、相似です。
C変換は使わずに、試しにそのままローレンツプロットしてみたわけですが規則性が見られましたね。ローレンツプロットは単純ですが強力です。初期値27以外でも、もっと大きな多数の初期値で、それぞれの最大値で規格化したローレンツプロットをして、まとめて右図のようなグラフを作成してみたら面白いかもしれません。左図も同時進行で。
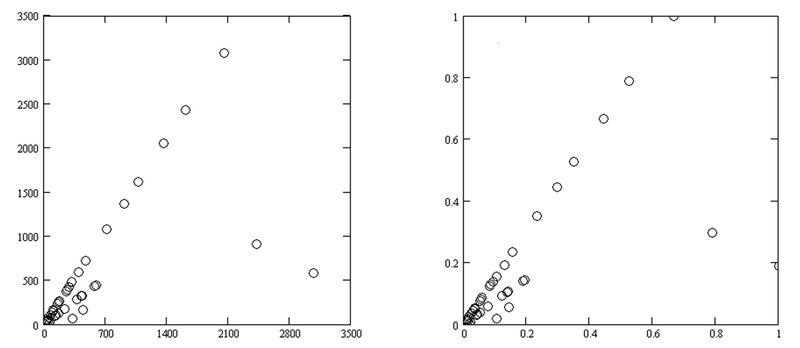
各点の値を最大値3077で割った場合のローレンツプロット(右)
では本論に入ります。
図6-3は第2章、ほか章でも紹介した図6-1上図の42個の正奇数値$${No}$$をC変換した値$${c(No)}$$を用いたグラフ、CS振動図です。
ローレンツプロットする前の段階で図6-1下図と比較して遥かに周期性や規則性が見られますから、ローレンツプロットすれば図6-2右図よりも、より規則性が見られるのは当然といえます。
C変換したローレンツプロットが図6-4でCS直線も含めたグラフは幾つかの前章で既に紹介しました。具体的には$${(c(27),c(41))}$$,$${((c(41),c(31))}$$, $${\cdots}$$ $${(c(53),c(5))}$$,$${(c(5),c(1))}$$の計41個の値をプロットしたグラフです。
$${c(No)}$$は0以上1未満の値ですが、図6-2右図のように最大値で規格化した値ではありません。C変換そのものが本質的に$${No}$$値を0以上1未満の値へと導きます。
6.1.2 CSプロットクモの巣グラフの見方
図6-4にCS直線、$${ f_{c}(x) , f_{s}(x)}$$(実線)を加え、さらにクモの巣グラフとしたのが図6-5です。
$$
\begin{array}{}
&(6.1)& & f_{c}(x)=\cfrac{3}{2}x+\cfrac{1}{2}& &(0\le x <1/3)& \\\\\
&(6.2)& & f_{s}(x)=\cfrac{3}{4}x-\cfrac{1}{4}& &(1/3\le x <1)
\end{array}
$$
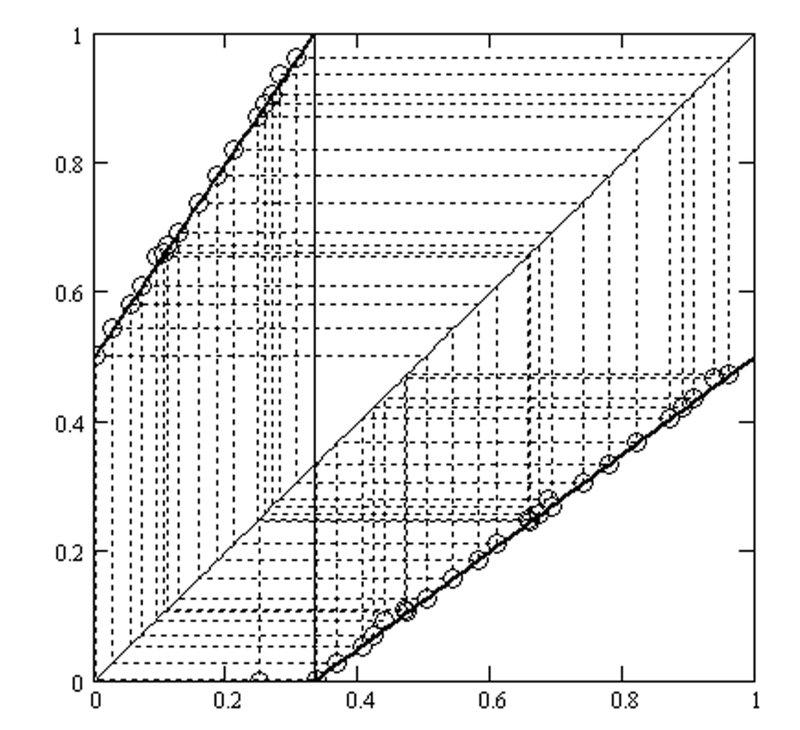
水平垂直補助線が多数ありすぎて、ステップ経緯がよくわかりませんので
最初の4点と最後の4点のクモの巣グラフを図6-6に示しました。
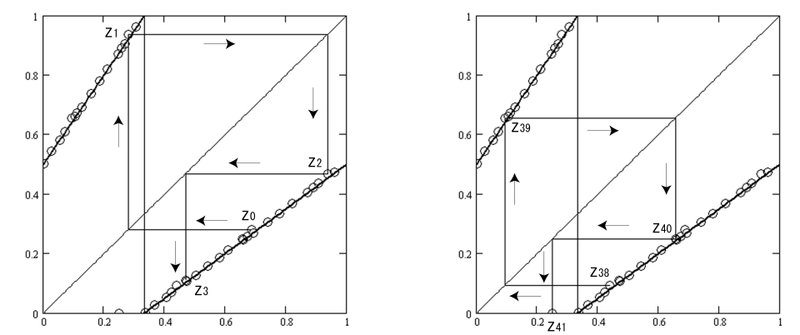
図6-6のz値は以下の通りです。
$${z_0=(c(27),c(41))}$$
$${z_1=(c(41),c(31))}$$
$${z_2=(c(31),c(47))}$$
$${z_3=(c(47),c(71))}$$
$${z_{38}=(c(23),c(35))}$$
$${z_{39}=(c(35),c(53))}$$
$${z_{40}=(c(53),c(5))}$$
$${z_{41}=(c(5),c(1))}$$
第3章で正奇数$${mo}$$に1ステップで到達する奇数列を$${cs(mo)}$$と定義しました。1ステップで$${1}$$に到達する$${cs(1)}$$は
$${cs(1)=\{1,\ 5, \ 21, \ 85, \cdots\}}$$で要素の数は無数にあります。
また$${c(1)=0}$$です。また$${c(No)=0}$$となる正奇数$${No}$$は$${1}$$以外はありません。従ってCS(ローレンツ)プロットでは最終点は必ずx軸上にあります。最終点以外の点は全てx軸よりも上にあります。$${1}$$は唯一1ステップで1に到達する周期1の数で$${(c(1),c(1))=(0,0)}$$で最終点しかありません。
さらに$${1}$$に到達後は一般コラッツ空間では$${1 \to 1\to 1 \to \cdots}$$ですので、そこまで拡張すると、最終到達点はどれも原点$${(0,0)}$$となります。
6.1.3 コラッツ予想と同値なCS空間上の命題(弱い命題)
以上から、一般コラッツ空間におけるコラッツ予想(奇数なら3倍して1を足す。偶数ならば2で割る。これを繰り返すとどんな正整数も有限回で1に到達する)と同値なCS空間上の命題(弱い命題)は、
**********************************
$${\bm{cs(1)}}$$に属する正奇数の要素を$${\bm{O}}$$とし、 そのC変換$${\bm{c(O)}}$$および正奇数$${\bm{No}}$$のC変換$${\bm{c(No)}}$$において、CS空間上のCSプロットでは、どんな$${\bm{c(No)}}$$も有限回でx軸上の点、$${\bm{(c(O),0)}}$$に到達し、最終到達点は原点$${(0,0)}$$となる。
**********************************
CSプロット点はCS直線上には全ての点が完全に乗っておらず、必ずずれており、近くに存在しています。
(強い命題ではCS直線上に乗ります!)。
偶数に関しては一般コラッツ空間でも必ずある奇数に到達するから考慮しなくてもいいわけですが、CS空間では例えば $${13 \to 40 \to 20 \to 10 \to 5 \to 16 \to 8 \to 4 \to 2 \to 1}$$ において$${c(40)=c(20)=c(10)=c(5)}$$や$${c(16)=c(8)=c(4)=c(2)=c(1)}$$などとなるため、偶数は必然的に考慮しなくてもよいことも第2章2.3で説明しました。
記事内容や証明で「なるほど」とお感じになったら、評価の程よろしくお願いいたします。今後の解析の奮起につながります。
第6章6.1までの変数・定義語・関数
$${N}$$、$${No}$$、総ステップ数、ステップ番号、
CS振動、C変換、CSプロット、CS直線式、3C+1変換、
3S+1変換、(一般)コラッツ空間、CS直線、S変換、CS空間、
tツリー、
ローレンツプロット、周期軌道、周期点、究極的な周期点、クモの巣図法、不動点、最終点、最終到達点
$${6t+5}$$型、$${6t+1}$$型、$${4t+3}$$型、$${8t+1}$$型、など
$${c(No)}$$、$${z_{s}}$$、$${f_{c}(x)}$$、$${f_{s}(x)}$$、距離$${D}$$、$${Nc}$$、$${Ns}$$、$${m_{o}}$$、$${m_{c}}$$、$${m_{s}}$$、$${t_{c}}$$、$${t_{s}}$$、$${t}$$、$${cs(mo)}$$、$${Mo}$$、$${s(Mo)}$$、$${O}$$、
この記事が気に入ったらサポートをしてみませんか?
