コラッツ予想解明への新解析手法の紹介8ー 問題の意味が小学生でもわかる数学の高額懸賞金歴史的未解決問題
第6章 コラッツ予想と同値なCS空間上の命題
今回の記事(8回目)をご覧になる前に「第1章 新手法の紹介の前に」をご覧ください。
また第1章には各章へのリンクが貼ってあります。
6.2 コラッツ予想と同値なCS空間上の命題(強い命題)
6.2.1 弱い命題は親の脛齧り but 成長が遥かに上回る
6.1ではコラッツ空間のコラッツ予想と同値なCS空間における弱い命題を紹介しました。
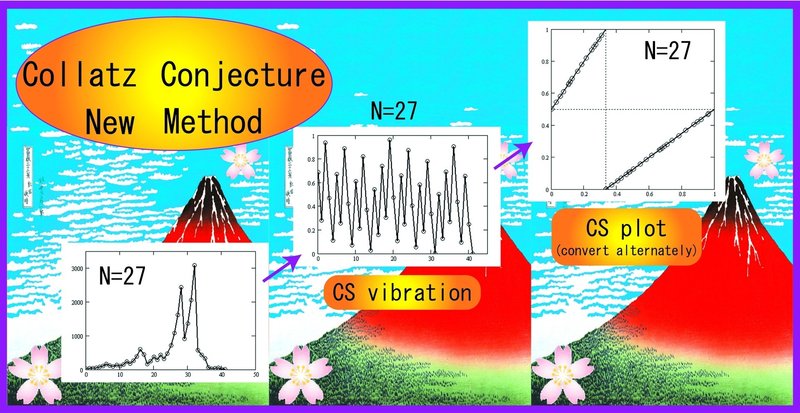
図6-7左図は縦軸$${c(No_{n+1})}$$、横軸$${c(No_n)}$$($${No}$$正奇数)の初期値27のローレンツプロットであるCSプロットです(図6-7右図は後で説明)。
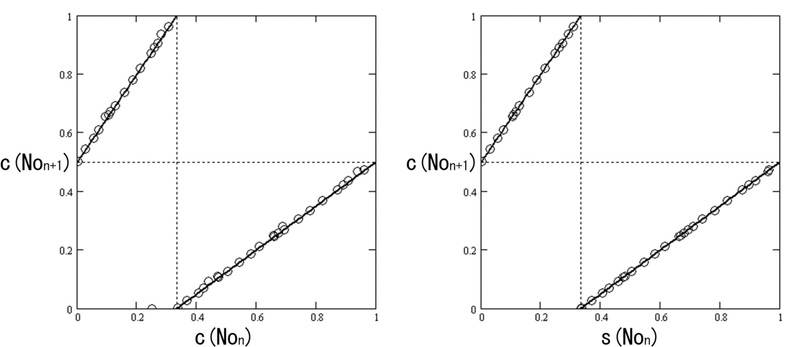
☆ 同値性よりももっと重要な特性は一般コラッツ空間の固有の奇数配列即ち無数の奇数からなる複雑に張り巡らされた奇数ツリーは、CS空間では奇数ツリーの全ての正奇数$${No}$$のC変換$${c(No)}$$のCSプロット点が最終点を除き、2直線(左図実線)の近くに全て存在することです。ここで1に到達する最終点のみ2直線から離れ、x軸上に存在しています。
一般コラッツ空間で$${1}$$に到達後は$${1 \to 1 \to 1 \cdots}$$で、また$${c(1)=0}$$ですので拡張すれば、最終到達点は原点$${(0,0)}$$となります。
一般コラッツ空間の奇数ツリーがCS空間でのCSプロットでは2直線でのみ近似できることは、コラッツ予想解明へ一歩前進したと言えるのではないでしょうか。☆
では弱い命題の方はどうでしょうか。これは弱い命題よりも、命題そのものが弱いのです。その理由は弱い命題は最初から最後まで親のすねをかじっているからです。
どういう意味かといいますと
弱い命題:
$${\bm{cs(1)}}$$に属する正奇数の要素を$${\bm{O}}$$とし、そのC変換$${\bm{c(O)}}$$および正奇数$${\bm{No}}$$のC変換$${\bm{c(No)}}$$において、どんな$${\bm{c(No)}}$$も有限回でx軸上の点、$${\bm{(c(O),0)}}$$に到達し、最終到達点は原点$${(0,0)}$$となる。
ここで、初期値から途中ステップ値の$${No}$$、$${O}$$も一般コラッツ空間(親)の正奇数値であって、CS空間(子)での$${c(No)}$$も$${c(O)}$$もこれ等正奇数値をC変換しただけだからです。最初から最後まで親のすねをかじっているではありませんか。それでも上記☆から☆内の今まで見出されていない特性はあるわけです。すねをかじっていますが、成長もあるわけです。この成長は☆から☆内の意味では大きな成長といいたいわけです。
6.2.2 強い命題は親から独立 and 更に大きく成長
子は親から生まれその遺伝要素は初期値の$${c(No)}$$で引き継がれ、その後は親から独立したいわけです。その後のステップでは親の$${No}$$も$${O}$$も使いたくない、CS空間内でのみステップ値を変えていき最終値にたどり着きたいわけです。それでこそ独立です。もちろん途中ステップ値は親の値$${No}$$を使った値に一致している必要があります。勝手な理論はNGです。数学ですから。そして☆から☆内よりももっと大きく成長したい。それが強い命題です。
第5章の1次元写像の定義は以下の通りでした。
数列 $${{x_0, x_1, x_2, \cdots, x_n, x_{n+1}, \cdots}}$$ において、$${x_{n+1}}$$が$${x_n}$$によってのみに決まる、$${x_{n+1}=f(x_n)}$$を考えます。
合成写像で表すと$${{x_0, f(x_0),f^2( x_0), \cdots, f^n(x_0), f^{n+1}(x_0), \cdots}}$$となります。 $${f^2( x_0)=f(f( x_0))}$$等です。
そうです。1次元写像関数$${f}$$が使えれば、$${n}$$ステップ後の値は$${f^n(x_0)}$$と初期値のみで求まり、親のすねをかじっていないわけです。立派に独立しています。
この$${f}$$に相当しているのが図6-7左図の実線で示したCS直線、$${ f_{c}(x) , f_{s}(x)}$$です。
$$
\begin{array}{}
&(6.3)& & f_{c}(x)=\cfrac{3}{2}x+\cfrac{1}{2} & &(0 \le x <1/3)&\\\\\
&(6.4)& & f_{s}(x)=\cfrac{3}{4}x-\cfrac{1}{4} & &(1/3 \le x <1)
\end{array}
$$
”もし”、初期値$${c(No_0)}$$も途中ステップ値$${c(No_n)}$$も全てがこの直線上に乗っていれば、$${n}$$ステップ後の値は$${f^n(c(No_0))}$$と求まり($${f}$$は$${f_c}$$または$${f_s}$$)、親からは独立していることになります。ところが図6-7左図を見てもわかるように直線上にはCSプロット点は乗っていないわけです。必ず直線より負のx方向にずれています。これは第2章2.3,第4章で説明しました。
一般コラッツ空間の正奇数$${No}$$はCS空間ではC変換した$${c(No)}$$となるわけですが、もう一つ重要な変数として第4章で登場したS変換した$${s(No)}$$があります。$${s(No)}$$は一般コラッツ空間では第3章で定義した$${cs(mo)}$$に現れる以下式の$${t_c, t_s}$$に相当しています。$${t}$$の特性については第3章で述べました。
$${(6.5) cs(6t_c+5)=\{4t_c+3,\ 16t_c+13, \ 64t_c+53, \ 256t_c+213, \cdots\}}$$
$${(6.6) cs(6t_s+1)=\{8t_s+1,\ 32t_s+5, \ 128t_s+21, \ 512t_s+85, \cdots\}}$$
CS直線式の$${x}$$は、実は$${c(No)}$$ではなくて$${s(No)}$$なのです。そしてこれをCS直線式の$${x}$$に代入した値$${f(s(No))}$$がs値になってくれればいいのですが、さらに厄介なことにc値に戻ってしまうのです(実はこれは本質的なことで、一般コラッツ空間の固有の数字配列(ツリー)も含んでしまっている理由の1つです)。
「なかなかやるなあ、c君、s君、fさんトリオ」です。図6-7右図で横軸がs、縦軸がcになっている理由です。これは以下セクションで説明しますが、いずれにしましてもc値とs値を交互に使うことにより一般コラッツ空間のコラッツルールに従う全ての正奇数$${No}$$がCS空間上では、全てCS直線式の上に乗ってしまうのです。最終点もx軸上ではなくCS直線式上にあります。
2次関数でもなく他関数でもなく直線上に乗ってしまう以上の規則性はありません。リーマン予想の「リーマンゼータ関数の自明でないゼロ点は全て実部が$${1/2}$$の直線上にある」ではありませんが、「コラッツルールに従う全ての正奇数$${No}$$がCS空間上では、全てCS直線上に乗る」です。
前者はこれが証明できれば素数には規則性があることになります。後者は証明しており、一般コラッツ空間のコラッツルールに基づく数字配列にはより一層の規則性があると言えたのではないでしょうか。
ネット上では多数の初期値から1に到達するまでの全ての数字を集めたグラフなどで規則性が見出されていますので、「より一層の」規則性なわけですが、新手法では1つの初期値でも規則性が見出されたわけです。ただ本題はそこにあるわけではありませんが。これ程の規則性が見出されたわけですから、2歩以上も3歩以上も解明に向けて前進できた、と考えたいです(1歩以上は弱い命題)。
コラッツ予想の最終的に1に到達する、とは素数の規則性と対比させた場合、インパクトの差はありますが、
コラッツ予想の数字配列の並び方に規則性があることは証明できた。また素数ではその並び方に規則性があることはリーマン予想が証明できた(仮想)からわかった。その次のステップの素数数列、n番目の素数は何か、に相当するのはコラッツ予想では任意の正奇数$${No}$$を初期値とした総ステップ数は幾つか、に対応しているということになりますかね。その前の最終的に1に到達する、は何に対応しているのでしょうか。余談ではありますが。
初期値$${s(No_0)}$$を与えてやればCS直線式の$${f}$$を使って(より正確には次セクションで紹介する$${g}$$も使って)、途中ステップの値も全て計算できるわけです。これが、親から独立 and さらに大きく成長、の意味するところです。
6.2.3 CS交互変換プロット
説明には親である一般コラッツ空間の正奇数$${No}$$を用い、そのC変換、S変換である$${c(No)}$$、$${s(No)}$$を使った方がわかりやすいので、これらを使用して説明します。
親から独立したCS直線式を用いた漸化式は
$${(6.7) \bm{ c(No_{n+1})=f(s(No_n))}}$$
ここで、$${f}$$は$${f_c}$$または$${f_s}$$、$${n}$$は$${0}$$以上の整数。
(6.7)式を用いてプロットしたグラフが図6-7右図です。cとsが入っているため、以下で示すように通常のローレンツプロットとはなりません。
これをCS交互変換ローレンツプロット、略してCS交互変換プロットと呼ぶことにします。
初期値27を例にとり最初の3点と最後の3点のCS交互変換プロットを図6-8に示します。
$${27 \to 41 \to 31 \to 37 \cdots \to 35 \to 53 \to 5 \to 1 }$$で42点、
ステップ番号は$${0,1, \cdots 41}$$の最初の3点と最後の3点です。
通常のローレンツプロットと違って複雑です。左図で説明すると通常のローレンツプロットは2と4は一致、6と8は一致しています。またx軸に向かう線はありません。x軸に向かう線を記す場合もありますが、クモの巣グラフの更に補助線でx座標値を見やすくするためのガイド線です。
一方、クモの巣グラフを水平垂直線で記す(一番わかりやすい)のであれば、CS交互変換プロットでは必要な線となります。ただし式としては(6.7)であり、見た目は通常の1次元線形写像と変わりはありません。
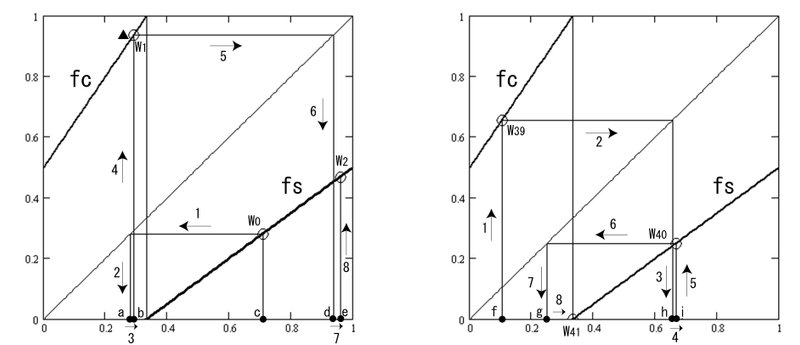
ここで上図$${a \to b}$$のようにx軸上でc値をs値に変える関数$${g}$$を定義しておく方が説明もわかりやすくなります。
$${(6.8) \bm{ s(No_n)=g(c(No_n))}}$$
CS交互変換プロットでは$${\bm{c(No_n)}}$$がx軸上で$${\bm{g}}$$により$${\bm{s(No_n)}}$$に変わります。$${\bm{s(No_n)}}$$は$${\bm{f}}$$により$${\bm{c(No_{n+1})}}$$に変わります。$${\bm{c(No_{n+1})}}$$は
y値ですが$${\bm{y=x}}$$によりx値になります。$${\bm{c(No_{n+1})}}$$はx軸上で$${\bm{g}}$$により$${\bm{s(No_{n+1})}}$$に変わります。これを初期値$${\bm{c(No_0)}}$$から順次繰り返していきます。
以下、図6-8内のwやa、bほか値の中身が長々と示されていますが
上記太字で示された内容を図6-8で確認するための式です。
図6-8の各wの中身は以下の通りです。
wのx座標がs値、y座標がc値になっています。
s値が$${f}$$によりc値になります。
s値が$${1/3}$$未満なら$${f_c}$$、$${1/3}$$以上なら$${f_s}$$を使用。
$${w_0=(s(27),c(41))}$$ ここで、 $${c(41)=f_s(s(27))}$$
$${w_1=(s(41),c(31))}$$ $${c(31)=f_c(s(41))}$$
$${w_2=(s(31),c(47))}$$ $${c(47)=f_s(s(31))}$$
$${w_{39}=(s(35),c(53))}$$ $${c(53)=f_c(s(35))}$$
$${w_{40}=(s(53),c(5))}$$ $${c(5)=f_s(s(53))}$$
$${w_{41}=(s(5),c(1))}$$ $${s(5)=1/3 , c(1)=0}$$
また$${a, b, c, \cdots, i}$$はx軸上の点ですが、その値は以下の通りです。
$${a=c(41), b=s(41), c=s(27), d=c(31), e=s(31)}$$
$${f=s(35), g=c(5), h=c(53), i=s(53)}$$
$${b, c, e}$$および$${f, i}$$はプロット点〇のx座標でs値。
$${a, d}$$および$${g, h}$$はプロット点〇のy座標に等しく、c値。
$${a}$$と$${b}$$の値は同じ正奇数値$${No}$$のc値とs値の関係で$${a < b}$$
$${d}$$と$${e}$$の値の関係、および$${h}$$と$${i}$$の値の関係も同様で
$${d < e}$$, $${h < i}$$
グラフ内の出発点$${c, f}$$はs値ですが、$${a}$$と$${b}$$、$${d}$$と$${e}$$、$${h}$$と$${i}$$の関係同様に、負方向隣にc値があります。
$${f}$$と$${g}$$を交互に用いた写像をCS写像とよぶことにします。
(6.7)式、(6.8)式ではわかりやすくするため、親である一般コラッツ空間の$${No_n}$$を用いて説明しましたが、CS空間での$${c(No_n)}$$値は写像$${g}$$と$${f}$$を交互に使用するCS写像により、初期値$${c(No_0)}$$から全て求めることができます。
初期値27の場合、最終プロット点は$${(s(5), c(1))}$$です。しかし初期値がどんな正奇数$${No}$$でも同一の値になります(初期値1でもです)。これは説明しておく必要があります。
一般コラッツ空間で1ステップで1に到達する数は(6.6)式で$${t_s=0}$$とした、$${cs(1)=\{1,\ 5, \ 21, \ 85, \cdots\}}$$です。要素の数は無数にありますが、それを表す代表とも言える値が$${t_s=0}$$です。$${cs(1)}$$に限らず、$${t_c}$$も含め、これ等$${t}$$値と$${cs}$$とは1対1に対応しています。
$${cs(1)}$$の要素のc変換値$${c(1), c(5), c(21), c(85) \cdots}$$は全て異なりますが、全てのs値は同じ値になります。$${s(1)=s(5)=s(21)=s(85) \cdots}$$です。そしてその値が$${\cfrac{1}{3}}$$(x座標)です。y座標は$${c(1)=0}$$なので最終点は$${\left(\cfrac{1}{3},0\right)}$$となります。この点は$${f_s(x)}$$上の端点に一致します。
弱い命題では最終点はx軸上にあり、初期値が異なれば$${cs(1)}$$の要素のいずれかになり無数にありました。最終到達点は原点$${(0,0)}$$でした。一方、一般コラッツ空間の最終値が$${1}$$である初期値ならば(現時点ではコラッツ「予想」なので)、CS空間では最終点および最終到達点はどんな初期値でも$${\bm{\left(\cfrac{1}{3},0\right)}}$$となります。
6.2.4 コラッツ予想と同値なCS空間上の命題(強い命題)
以上から、一般コラッツ空間におけるコラッツ予想
(奇数なら3倍して1を足す。偶数ならば2で割る。これを繰り返すとどんな正整数も有限回で1に到達する)
と同値なCS空間上の命題(強い命題)は、
**********************************
任意の正奇数$${\bm{No}}$$を初期値としたCS空間でのC変換$${\bm{c(No)}}$$において、CS交互変換プロットを使ったCS写像では
どんな$${\bm{c(No)}}$$も有限回で
$${\bm{\left(\cfrac{1}{3},0\right)}}$$に到達する。
**********************************
6.1の繰り返しになりますが偶数に関しては一般コラッツ空間でも必ずある奇数に到達するから考慮しなくてもいいわけですが、
CS空間では例えば $${13 \to 40 \to 20 \to 10 \to 5 \to 16 \to 8 \to 4 \to 2 \to 1}$$ において$${c(40)=c(20)=c(10)=c(5)}$$や$${c(16)=c(8)=c(4)=c(2)=c(1)}$$などとなるため、偶数は必然的に考慮しなくてもよいです。
一般コラッツ空間の(6.5)式の各要素を区別するのは正整数$${p}$$ですが(第3章)、各要素のc値も$${p}$$の関数であり、実はs値は$${p}$$を無限大にした時のc値の極限値になっています(第2章2.3及び第4章)。(6.6)式でも同様です。そしてs値はCS交互変換プロットにおいて、CS直線式$${f}$$を使うためのc値の変換値的な役目を担っています。$${s=g(c)}$$。c値があってこそs値があるわけです。c値とは独立にs値があるわけではありません。
第5章までの内容から上記内容は理解できます。唯一$${c(No)}$$から$${s(No)}$$を求める方法については、式としては説明しましたが具体的な数値としてc値が与えられたときのs値の求め方については説明していませんが、第5章までがわかれば導くことができるはずです。(6.7)式に比べれば宿題レベルです。また上記内容ではそれは・・章で説明したなど何か所かあり、細かい説明や証明は後回しにして、いすれにしても等をいれ、6.2としましては強い命題まで、主として流れがわかるように説明しました。
強い命題を理解するための定量的追加説明は、第2章から第6章までの重要公式を列挙し、これに適宜追加説明を加えていくという形式で、6.2.5にまとめ、有料記事とさせていただきました。
記事内容や証明で「なるほど」とお感じになったら、評価の程よろしくお願いいたします。今後の解析の奮起につながります。
第6章6.2までの変数・定義語・関数
$${N}$$、$${No}$$、総ステップ数、ステップ番号、
CS振動、C変換、CSプロット、CS直線式、3C+1変換、
3S+1変換、(一般)コラッツ空間、CS直線、S変換、CS空間、
tツリー、
ローレンツプロット、周期軌道、周期点、究極的な周期点、
クモの巣図法、不動点、最終点、最終到達点、
CS交互変換プロット、CS写像、$${\left(\cfrac{1}{3},0\right)}$$、
$${6t+5}$$型、$${6t+1}$$型、$${4t+3}$$型、$${8t+1}$$型、など
$${c(No)}$$、$${z_{s}}$$、$${f_{c}(x)}$$、$${f_{s}(x)}$$、距離$${D}$$、$${Nc}$$、$${Ns}$$、$${m_{o}}$$、$${m_{c}}$$、$${m_{s}}$$、$${t_{c}}$$、$${t_{s}}$$、$${t}$$、$${cs(mo)}$$、$${Mo}$$、$${s(Mo)}$$、$${O}$$, $${f}$$、$${g}$$、 $${w_{s}}$$、
6.2.5 セクション6.2 全般の定量的追加説明
ここから先は
¥ 800
この記事が気に入ったらサポートをしてみませんか?
