New Method for Solving the Collatz Conjecture 8 with High-Prize Money
Chapter 6: Propositions on CS-Space Equivalent to the Collatz Conjecture
Please read "Introduction to a New Method in Chapter 1 (article 1)"
before reading Chapter 6 (article 8).
Chapter 1 also posts links to each chapter.
When translating from Japanese to English, subtle nuances of the original articles may not be fully conveyed. If you would like to view the original Japanese articles, please see Chapter 1 of Japanese Article 1.
Summary Video of the New Method in English
6.2 Proposition on CS-Space Equivalent to the Collatz Conjecture (Strong Proposition)
6.2.1 Weak propositions are parasites of their parents, but their growth far exceeds that of their parents.
In Section 6.1, a weak proposition in the CS-space equivalent to the Collatz conjecture in the Collatz space is introduced. The left figure of Figure 6-7 is a CS-plot, which is a Lorenz plot of the initial value 27 with the vertical axis $${c(No_{n+1})}$$ and the horizontal axis $${c(No_n)}$$ ($${No}$$ is a positive odd number). (The right figure of Figure 6-7 will be explained later.)
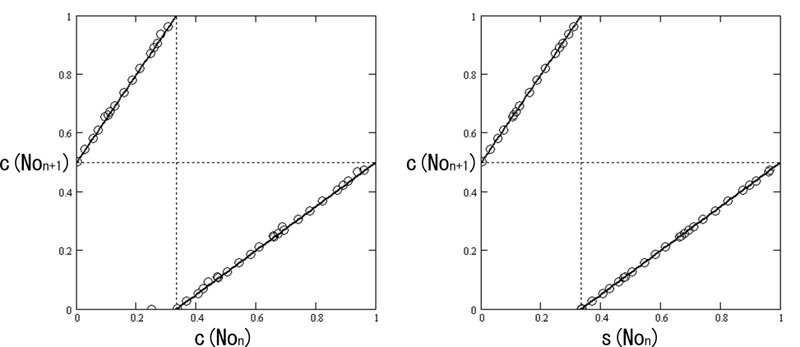
☆The most important property, more than equivalence, is that all odd number sequences in the general Collatz space, (namely the complex odd number trees consisting of an infinite number of odd numbers), exist near two straight lines (solid lines in the left figure) in the CS-plot of the CS-transform $${c(No)}$$ of all odd numbers $${No}$$ in the CS space, except for the final point. Here, only the final point that reaches 1 is away from the two straight lines and exists on the x-axis.☆
In the general Collatz space, after reaching $${1}$$, the sequence becomes $${1 \to 1 \to 1 \cdots}$$. Additionally, since $${c(1)=0}$$, the ultimate point is the origin (0,0) when extended.
Can it be said that the fact that the odd number tree of the general Collatz space can be approximated by only two straight lines in the CS-plot of the CS-space is a step forward in solving the Collatz conjecture? ☆
How about the weaker proposition? The proposition itself is weaker than the weak proposition. The reason is that the weak proposition relies on its parent from beginning to end.
The meaning is as follows:
Weak Proposition:
Under the C-transformations, $${\bm{c(O)}}$$ and $${\bm{No}}$$ for positive odd integers, $${\bm{O}}$$ and $${\bm{No}}$$, any $${\bm{c(No)}}$$ in the CS-space reaches a point on the x-axis, $${\bm{(c(O),0)}}$$, in a finite number of steps, and the ultimate point is the origin $${(0,0)}$$.
Here, The reason is that the initial value, and the intermediate step values $${No}$$, $${O}$$ are also odd numbers in the general Collatz space (parent), and $${c(No)}$$ and $${c(O)}$$ in the CS-space (child) are simply the C-transforms of these odd numbers. Therefore, the weak proposition relies on its parent from beginning to end.
Even so, there are still characteristics that have not been found in the above ☆ from ☆. It relies on its parent, but it also grows. This growth can be said to be a significant growth in the sense of ☆ from ☆.
6.2.2 Strong propositions are independent of their parents and groweven larger.
The child is born from the parent and inherits its genetic elements in the initial value $${c(No)}$$. After that, the child wants to be independent from the parent. In the subsequent steps, the child does not want to use the parent's $${No}$$ and $${O}$$, and wants to change the step value only within the CS-space to reach the final value.
That's the essence of independence.
The intermediate step values must, of course, match the values obtained using the parent value $${No}$$. Arbitrary theories are not acceptable. This is mathematics. And the child wants to grow even more than the proposition within ☆ from ☆. That is a strong proposition.
The definition of a one-dimensional map in Chapter 5 is as follows:
Consider a sequence $${{x_0, x_1, x_2, \cdots, x_n, x_{n+1}, \cdots}}$$ where $${x_{n+1}}$$ is determined only by $${x_n}$$, that is, $${x_{n+1}=f(x_n)}$$.
Expressed in terms of composite functions, this becomes $${{x_0, f(x_0),f^2( x_0), \cdots, f^n(x_0), f^{n+1}(x_0), \cdots}}$$ where $${f^2( x_0)=f(f( x_0))}$$ and so on.
Yes, if the one-dimensional mapping function $${f}$$ can be used, the value after $${n}$$ steps can be obtained with only the initial value $${f^n(x_0)}$$, and it is not dependent on the parent. It is completely independent.
The solid line in the left figure of Figure 6-7, which represents the CS-line,
$${f_c(x), f_s(x)}$$, corresponds to this $${f}$$.
$$
\begin{array}{}
&(6.3)& & f_{c}(x)=\cfrac{3}{2}x+\cfrac{1}{2} & &(0 \le x <1/3)&\\\\\
&(6.4)& & f_{s}(x)=\cfrac{3}{4}x-\cfrac{1}{4} & &(1/3 \le x <1)
\end{array}
$$
If the initial value $${c(No_0)}$$ and all the intermediate step values $${c(No_0)}$$ are on this line, the value after n steps can be obtained as $${f^n(c(No_0))}$$ ($${f}$$ is $${f_c}$$ or $${f_s}$$), and it becomes independent from the parent.
However, as you can see in the left figure of Figure 6-7, the CS-plot points are not on the line. They are always shifted to the negative x direction from the line. This was explained in Section 2.3 of Chapter 2 and Chapter 4.
In the CS-space, the odd numbers $${No}$$ of the general Collatz space become $${c(No)}$$ after the C-transformation. However, another important variable that appeared in Chapter 4 is the S-transformed $${s(No)}$$.
In the general Collatz space, $${s(No)}$$ corresponds to $${t_c, t_s}$$ in the following equation that appears in $${cs(mo)}$$ defined in Chapter 3:
The properties of $${t}$$ were described in Chapter 3.
$${(6.5) cs(6t_c+5)=\{4t_c+3,\ 16t_c+13, \ 64t_c+53, \ 256t_c+213, \cdots\}}$$
$${(6.6) cs(6t_s+1)=\{8t_s+1,\ 32t_s+5, \ 128t_s+21, \ 512t_s+85, \cdots\}}$$
The $${x}$$ in the CS-linear-equations is actually $${s(No)}$$, not $${c(No)}$$. It is desired that the value $${f(s(No))}$$ obtained by substituting this into the$${x}$$ of the CS-linear-equations becomes the s-value, but unfortunately, it turns out to be the c-value again (this is actually an essential point, and it is one of the reasons why the unique number sequence (tree) of the general Collatz space is also included).
"Well done, trio of Mr.c, Mr.s, and Ms.f!"
This is the reason why the horizontal axis is s and the vertical axis is c in the right figure of Figure 6-7.
This will be explained in the following sections, in any case, by using c-values and s-values alternately, all odd numbers $${No}$$ that follow the Collatz rule in the general Collatz space lie on the CS-linear-equations in the CS space.
The final point is also not on the x-axis, but on the CS-linear-equations.
There is no more regularity than that they lie on a straight line, not a quadratic function, not any other function.
Though it does not mean that "all non-trivial zeros of the Riemann zeta function lie on the straight line with real part $${1/2}$$", as in the Riemann hypothesis, it is the case that "all odd numbers $${No}$$ that follow the Collatz rule lie on the CS-line in the CS-space".
The former would show that there is a regularity to prime numbers if it could be proven.
The latter has been proven, and it could be said that there is a greater regularity in the arrangement of numbers based on the Collatz rule in the general Collatz space.
On the internet, regularities have been found in graphs and other data that collect the numbers from various initial values that reach 1. However, the new method has found regularities even with a single initial value. Therefore, the new method is "even more" regular. However, this is not the main point.
Since such regularities have been found, so it can be considered that significant progress has been made towards solving the problem, more than two or three steps forward (more than one step is a weak proposition).
While the ultimate goal of the Collatz conjecture, reaching 1, differs in impact from the regularities of prime numbers, the new method has proven that there is a regularity in the arrangement of its number sequence in the Collatz space . Similarly, (hypothetically proven) it has shown that there is a regularity in the arrangement of prime numbers in the Riemann hypothesis.
The next step for prime numbers, finding the nth prime number, can be compared to finding the total number of steps for any odd number $${No}$$ used as the initial value in the Collatz conjecture. What does the previous step, ultimately reaching 1, correspond to? This is a digression, though.
Given an initial value $${s(No_0)}$$, all intermediate step values can also be calculated using the CS-linear-equations $${f}$$ (or more precisely, $${g}$$ introduced in the next section). This is what "independent from the parent and further growth" means.
6.2.3 CS-alternating transformation plot
$${No}$$ is the odd number in the parent general Collatz space, and the following explanation provides a clearer understanding by using the C-transform, $${c(No)}$$, and S-transform, $${s(No)}$$.
The recursive formula using the CS-linear-equations independent of the parent is given by:
$${(6.7) \bm{ c(No_{n+1})=f(s(No_n))}}$$
Here, $${f}$$ is either $${f_c}$$ or $${f_s}$$ and $${n}$$ is a non-negative integer.
The graph plotted using (6.7) is shown in the right figure of Figure 6-7.
Due to the presence of c and s, it does not follow the conventional Lorenz plot, as shown below.
This will be referred to as the CS-alternating transformation Lorenz plot, or simply the CS-alternating transformation plot.
Figure 6-8 shows the CS-alternating transformation plot for the first and last three points, taking the initial value 27 as an example.
$${27 \to 41 \to 31 \to 37 \cdots \to 35 \to 53 \to 5 \to 1 }$$
There are 42 points in total, and the step numbers are the first and last three points of $${( 0,1, \cdots 41 )}$$
Unlike the conventional Lorenz plot, the CS-alternating transformation plot is more complex. As shown in the left figure, the conventional Lorenz plot has 2 and 4 coincide, and 6 and 8 coincide. It also does not have lines that go towards the x-axis. Although such lines may be drawn, they are simply guidelines for easier viewing of the x-coordinate values, that act as the auxiliary lines in addition to a cobweb plot.
On the other hand, if the cobweb plot is drawn with horizontal and vertical lines (which is the easiest to understand), these lines become necessary in the CS-alternating transformation plot. However, the equation is still (6.7), and the appearance is no different from a regular one-dimensional linear transformation.

of the CS-alternating transformation plot with an initial value of 27.
It is more convenient to define a function $${g}$$ that converts the c-value to the s-value on the x-axis, as shown in the figure above: $${a \to b}$$.
$${(6.8) \bm{ s(No_n)=g(c(No_n))}}$$
In the CS-alternating transformation plot:
$${\bm{c(No_n)}}$$ on the x-axis is converted to $${\bm{s(No_n)}}$$ by $${\bm{g}}$$.
$${\bm{s(No_n)}}$$is converted to $${\bm{c(No_{n+1})}}$$ by $${\bm{f}}$$.
$${\bm{c(No_{n+1})}}$$, which is a y-value, is converted to an x-value by $${\bm{y=x}}$$.
$${\bm{c(No_{n+1})}}$$ on the x-axis is converted to $${\bm{s(No_{n+1})}}$$ by $${\bm{g}}$$.
This process is repeated starting from the initial value $${\bm{c(No_0)}}$$.
The following shows the substance of w, a, b, and other values in Figure 6-8, in a long and detailed manner. These are used to verify the contents shown in bold above in Figure 6-8.
The contents of each w in Figure 6-8 are as follows.
The x-coordinate of w represents the s-value, and the y-coordinate represents the c-value.
The s-value is converted to the c-value using the function $${f}$$.
If the s-value is less than $${1/3}$$, $${f_c}$$ is used.
If the s-value is greater than or equal to $${1/3}$$, $${f_s}$$ is used.
$${w_0=(s(27),c(41))}$$ Here、 $${c(41)=f_s(s(27))}$$
$${w_1=(s(41),c(31))}$$ $${c(31)=f_c(s(41))}$$
$${w_2=(s(31),c(47))}$$ $${c(47)=f_s(s(31))}$$
$${w_{39}=(s(35),c(53))}$$ $${c(53)=f_c(s(35))}$$
$${w_{40}=(s(53),c(5))}$$ $${c(5)=f_s(s(53))}$$
$${w_{41}=(s(5),c(1))}$$ $${s(5)=1/3 , c(1)=0}$$
Additionally, $${a, b, c, \cdots, i}$$ are points on the x-axis with the following values:
$${a=c(41), b=s(41), c=s(27), d=c(31), e=s(31)}$$
$${f=s(35), g=c(5), h=c(53), i=s(53)}$$
$${b, c, e}$$ and $${f, i}$$ are the X coordinates of plot point 〇, and they represent s-values.
$${a, d}$$ and $${g, h}$$ are equal to the Y coordinates of plot point 〇 , and they represent c-values.
The values of $${a}$$ and $${b}$$ follow the relationship between c-values and s-values of the same odd number $${No}$$, where $${a < b}$$.
The relationship between the values of $${d}$$ and $${e}$$, and the relationship between the values of $${h}$$ and $${i}$$, are similar, with $${d < e}$$ and $${h < i}$$.
The starting points $${c, f}$$ have s-values.
Similar to the relationship between $${a}$$ and $${b}$$, $${d}$$ and $${e}$$, and$${h}$$ and $${i}$$, there are c-values next to them in the negative direction.
A mapping that uses f and g alternately is called a CS-map.
Equations (6.7) and (6.8) use the $${No_n}$$ of the parent general Collatz space for clarity. However, all $${c(No_n)}$$ values in the CS-space can be obtained from the initial value $${c(No_0)}$$ using the CS-map, which alternately applies the maps $${g}$$ and $${f}$$.
For the initial value 27, the final plot point is $${(s(5), c(1))}$$. However, the same value is obtained for any odd number $${No}$$ as the initial value (even for the initial value 1). This needs to be explained.
The set of numbers that reach 1 in one step in the general Collatz space, as defined by $${t_s=0}$$ in Equation (6.6), is $${cs(1)=\{1,\ 5, \ 21, \ 85, \cdots\}}$$. While the number of elements is infinite, the value $${t_s=0}$$ can be considered a representative value for this set. This one-to-one correspondence between $${t}$$ values and $${cs}$$ sets holds not only for $${cs(1)}$$ but also for $${cs(m_o)}$$, including $${t_c}$$.
The element c-conversion values of $${cs(1)}$$, which are $${c(1), c(5), c(21), c(85) \cdots}$$, are all different. However, all s values are
the same,
$${s(1)=s(5)=s(21)=s(85) \cdots}$$, and this value is $${\cfrac{1}{3}}$$ (x-coordinate). Since the y-coordinate is $${c(1)=0}$$, the final point is
$${\left(\cfrac{1}{3},0\right)}$$. This point coincides with the endpoint of $${f_s(x)}$$.
In the weak proposition, the final point exists on the x-axis and can be any element of $${cs(1)}$$, which are infinite in number, depending on the initial value. The ultimate point is the origin $${(0,0)}$$.
On the other hand, for initial values whose final point in the general Collatz space is $${1}$$ (which is currently the Collatz "conjecture"), the final point and ultimate point in the CS-space will be $${\bm{\left(\cfrac{1}{3},0\right)}}$$ for any initial value.
6.2.4 Strong proposition on CS-space equivalent to the Collatz conjecture
Based on the above, the Collatz conjecture on the general Collatz space that states "For any odd integer, triple it and add 1. For any even integer, divide it by 2. Repeat this process and any positive integer will eventually reach 1 in a finite number of steps" is equivalent to the following proposition on the CS- space (strong proposition) :
**********************************
In the C-transformation $${\bm{c(No)}}$$ in CS-space with an arbitrary positive odd number $${\bm{No}}$$ as the initial value, using the CS-map with CS-alternating transformation plots, any $${\bm{c(No)}}$$ will reach the ultimate point $${\bm{\left(\cfrac{1}{3},0\right)}}$$ in a finite number of times.
**********************************
The following is a repetition of Section 6.1. In the case of even numbers, it is not necessary to consider them in the general Collatz space because they always reach an odd number.
However, in the CS space, even numbers can be inevitably ignored for the following reasons.
For example, in the sequence $${13 \to 40 \to 20 \to 10 \to 5 \to 16 \to 8 \to 4 \to 2 \to 1}$$, $${c(40)=c(20)=c(10)=c(5)}$$ and $${c(16)=c(8)=c(4)=c(2)=c(1)}$$ are inevitably true.
Each element of (6.5) in the general Collatz space is distinguished by the positive integer p (Chapter 3), and the c-value of each element is also a function of p.
In fact, the s-value is the limit value of the c-value as p approaches infinity (Chapter 2.3 and Chapter 4). The same is true for equation (6.6).
The s-value also plays a role as a conversion value of the c-value for using the CS-linear-equations $${f}$$ in the CS-alternating transformation plot.
$${s=g(c)}$$.
The s-value exists only if the c-value exists. The s-value does not exist independently of the c-value.
The content above can be understood from the contents up to Chapter 5.
The method of obtaining s(No) from c(No) has been explained in terms of equations, but the method of obtaining the s-value when a specific numerical value is given for the c-value, has not been explained. However, with an understanding of Chapters 1 to 5, it should be possible to derive it.
Compared to Equation (6.7), this is a homework level problem.
Several places in the above content state that it is explained in xx chapter, the detailed explanation and proof are postponed, and the phrase "in any case" is used. As for Section 6.2, the flow leading to the strong proposition is explained in a mainly understandable way.
Quantitative additional explanations for understanding the strong proposition are summarized in Section 6.2.5 in the form of listing important formulas from Chapters 2 to 6 and adding additional explanations as appropriate. This section is provided as a paid article.
If you find the content of the article to be insightful, please consider giving it a positive rating. This will encourage further analysis.
Variables, Definitions, and Functions up to Section 6.2 in Chapter 6:
$${N}$$, $${No}$$,
total number of steps, step number, CS-vibration, C-transformation,
CS-plot, CS-linear-equations, 3C+1 transformation, 3S+1 transformation,
(general) Collatz space, CS-line, S-transformation, CS-space, t-tree,
Lorenz plot, period orbit, periodic point, eventually periodic point,
cobweb diagram, fixed point, final point, ultimate point,
CS-alternating transformation plot, CS-map, $${\left(\cfrac{1}{3},0\right)}$$,
type $${6t+5}$$, $${6t+1}$$, $${4t+3}$$, $${8t+1}$$, etc.
$${c(No)}$$, $${z_{s}}$$, $${f_{c}(x)}$$, $${f_{s}(x)}$$, distance$${D}$$,
$${Nc}$$, $${Ns}$$, $${m_o}$$, $${m_{c}}$$, $${m_{s}}$$, $${t_{c}}$$, $${t_{s}}$$, $${t}$$, $${cs(m_o)}$$, $${Mo}$$, $${s(Mo)}$$, $${O}$$, $${f}$$, $${g}$$, $${w_{s}}$$,
The new method is introduced in Articles 1-10 and Chapters 1-8.
The translation from Japanese to English has been completed for all articles, both free and paid. (April 2024)
6.2.5 Quantitative additional explanation for Section 6.2
ここから先は
¥ 800
この記事が気に入ったらサポートをしてみませんか?
