コラッツ予想解明への新解析手法の紹介9ー 問題の意味が小学生でもわかる数学の高額懸賞金歴史的未解決問題
今回の記事(9回目)をご覧になる前に「第1章 新手法の紹介の前に」をご覧ください。
また第1章には各章へのリンクが貼ってあります。
第7章 コラッツ予想は攻略できる?できそう?できるかも?
7.1 正攻法では牙城を崩すのは難しい
コラッツ予想に取り組んで1年半位でしょうか。
手書きの1センチ厚ノートで10冊は計算したりまとめたりしていましたね。見直した時に時が経つと、字も下手なので、何の計算だったかな、になりかねないので適宜Latex使ってまとめ直していました。おかげで解析内容は
いつでも見直すことができます。
それ以前はモンハンとかに凝ったりしていたのですが、章タイトルが攻略になっているのはそのなごりです(笑) 歴史的未解決問題の世界を知ってからはすっかりこれにはまってしまいましたね。
まとめてみてわかったことは、第3章のようなオーソドックスな方法では
コラッツ予想は解けそうだ、というところまではいくのですが、残り数パーセントで壁にぶち当たるわけです。いろいろ試しましたが壁に当たるわけです。それはそうかなと。80年以上も前からプロアマ数学者が解析しているわけですから一般的な方法では牙城は崩せないのも当然といえば当然です。
ためになる論文はあります。例えば笑わない数学番組で紹介した論文です。「コーネリアス・エベレットの証明は4ページと短く、それほど高度な数学は使用されていません。英語の論文ですが興味がある方はどうぞ。」とありました。
https://www.sciencedirect.com/science/article/pii/0001870877900871
自然数全体をそれぞれ初期値とみなして途中ステップの値を規則に従い1と0で表わしていくと自然数全体が何かしらの調和のとれた、何と言いますか、波のように1と0の規則性が見えるんですね。コラッツ予想に取り組んでいる読者には必読ですね。前半2ページ半部分ですが、具体例も少なく読んだだけではわかりにくく、手書きノートに書いてはパソコンで確かめました。規則性には驚きですね。
後半はどの数も最後は1と0が半々出現するという仮定の基に確率的に”ほとんど”全ての数に対してコラッツ予想は正しいと結んでいます。文献は1つしかなく、そこに基にした確率手法の内容が記載されているようです。確率論では完全証明にはたどり着けませんから、”ほとんどの”数で予想は正しいとしています。
ネット記事では、証明した、とかありますが、アクセス数も増えるのはいいでしょうが、何でこれで証明になっているのという記事は多々あります。
記事の段階ではいいですが、プレプリントでも確率論を用いているのに証明できたとかありますが、確かにアクセス数は増えるでしょうね。しかし他論文では引用されないですよね、コラッツ予想に関するプレプリントや論文の文献にコラッツ予想を証明した論文を引用するのもおかしな話です。
テレンス・タオのプレプリントや論文も読んではいませんが確率論を用いており、完全証明には遠く及ばないと自身で述べています(第1章)。参考文献としてよく引用されています。天才ですから、それも引用される理由ですね。
フェルマーの最終定理は360年以上未解決だったわけですが、アンドリュ・ワイルズが谷村-志村予想を証明し1995年に決着を付けたわけです。
四色問題は1852年にフランスの数学者フランソワ・ガスリーによって発案され、プログラムを用いた証明と検証が1976年から2004年まで行われ四色問題は解決したと捉えられています(Wikipedia)
谷村-志村予想が出るまではとか、コンピュータの発展とか、など待っていては、この世にはもういないわけです。
正攻法ではいいところまではいくが、解けそうで解けないわけです。長い年月に渡って未解決であるという歴史が証明しているわけです。いつかは解決できるかもしれませんが、解決に取り組んでいる皆さんは存命中に解決したいわけです、当然です。子に託したいわけではないわけです。
であれば理論体系が確立している別分野で解けないか、も十分に選択肢の1つになります。グレゴリー・ペレルマンはポアンカレ予想を正攻法ではなく物理分野で解いたわけですね。
今回の新手法は、一般コラッツ空間のコラッツ予想と同値な命題を理論体系が確立している(もちろん進展しています)カオス力学手法が使えるCS空間上の命題の変換に成功したわけです。しかも0以上1未満の1次元線形写像というカオス力学では導入部分に相当しています。
あとは
カオス理論を使って解けるか
です。
7.2 ベルヌーイシフト(二進変換)写像
ネットでは2進数を用いてコラッツ予想に取り組んでいる人達もいますので、カオス力学のベルヌーイシフト(2進変換)写像を紹介しておきます。直接コラッツ予想と関係しているわけではありませんが、単純な線形写像から類似性が見えて面白いですね。
$${ 2x (A:0 \le x < 1/2)}$$
$${(7.1) B(x)=}$$
$${ 2x-1 (B:1/2 \le x < 1)}$$
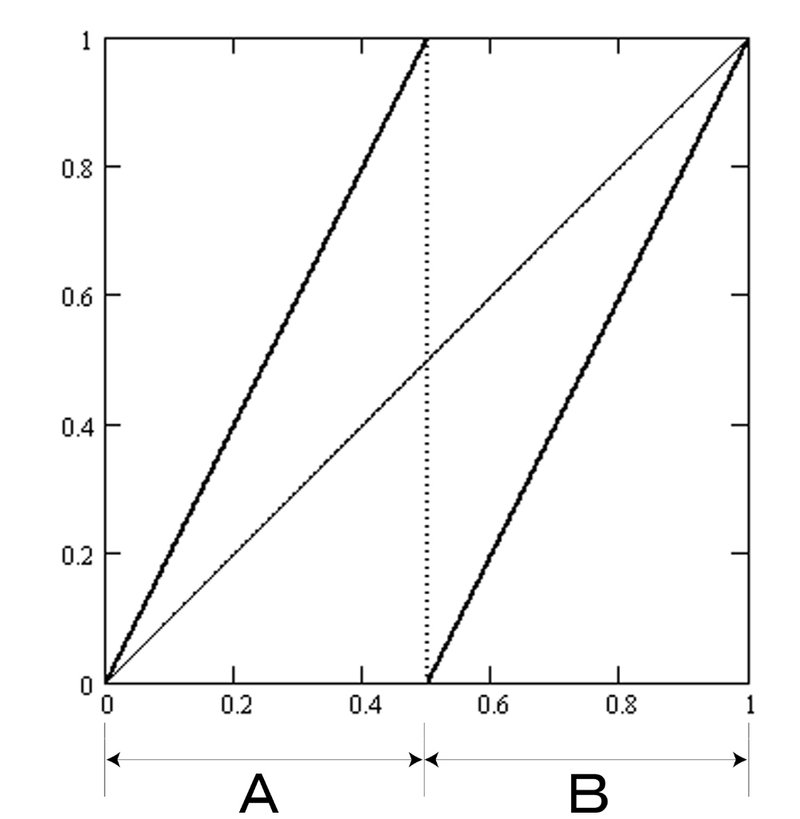
$${0 \le x < 1}$$の2進数を$${x=(0.x_1x_2\cdots x_n \cdots)_2}$$ $${(x_n=0, 1)}$$
で表すことにします。
10進小数では$${x=\cfrac{x_1}{2^1}+\cfrac{x_2}{2^2}+\cdots+\cfrac{x_n}{2^n}+\cdots}$$です。
$${x=(0.x_1x_2\cdots x_n \cdots)_2}$$において小数点1桁目$${x_1}$$が0か1かで分類します。
(a1)$${x_1=0}$$のとき
$${x_1=0}$$ならば$${x<\cfrac{1}{2}}$$なので
$${B(x)=2x=2\left(\cfrac{0}{2^1}+\cfrac{x_2}{2^2}+\cdots+\cfrac{x_n}{2^n}+\cdots\right)}$$
$${ =\cfrac{x_2}{2^1}+\cfrac{x_3}{2^2}+\cdots+\cfrac{x_{n+1}}{2^{n}}+\cdots =(0.x_2x_3\cdots x_{n+1} \cdots)_2}$$
(a2)$${x_1=1}$$のとき
$${x_1=1}$$ならば$${\cfrac{1}{2} \le x < 1}$$なので
$${B(x)=2x-1=2\left(\cfrac{1}{2^1}+\cfrac{x_2}{2^2}+\cdots+\cfrac{x_n}{2^n}+\cdots\right)-1}$$
$${ =\cfrac{x_2}{2^1}+\cfrac{x_3}{2^2}+\cdots+\cfrac{x_{n+1}}{2^{n}}+\cdots =(0.x_2x_3\cdots x_{n+1} \cdots)_2}$$
(a1)、(a2)から2進変換は$${\bm{x=(0.x_1x_2\cdots x_n \cdots)_2}}$$を左に1つずらしていく(shift)変換と言えます。
$${B(x)=(0.x_2x_3\cdots x_{n+1} \cdots)_2}$$
$${B^2(x)=(0.x_3x_4\cdots x_{n+2} \cdots)_2}$$
$${B^3(x)=(0.x_4x_5\cdots x_{n+3} \cdots)_2}$$
$${B^n(x)=(0.x_{n+1}x_{n+2}\cdots x_{2n} \cdots)_2}$$
次に10進小数の有限値、有理数、無理数等とベルヌーイシフト写像との関係を見てみます。
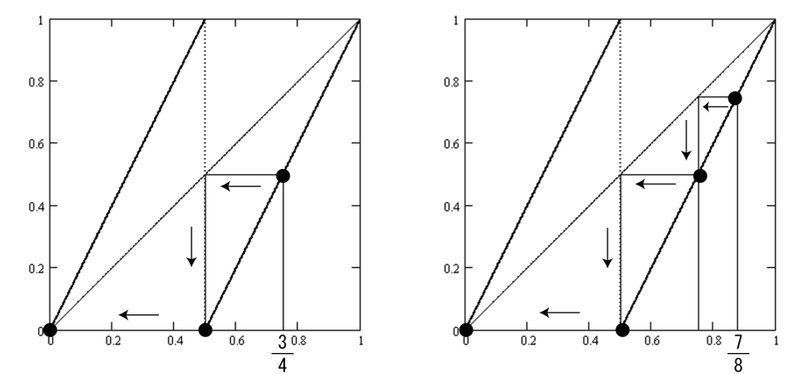
(b1)10進小数で分母が2のべき乗なら2進小数は有限値になり最終的に原点$${(0,0)}$$に到達します。
$${\cfrac{3}{4}=\cfrac{1}{2^1}+\cfrac{1}{2^2}=(0.11)_2}$$
$${B}$$を作用させると、$${\cfrac{3}{4} \to \cfrac{2}{4} \to 0 \to 0 \cdots}$$
$${\cfrac{7}{8}=\cfrac{4+2+1}{8}=\cfrac{1}{2^1}+\cfrac{1}{2^2}+\cfrac{1}{2^3}=(0.111)_2}$$
$${B}$$を作用させると、$${\cfrac{7}{8} \to \cfrac{6}{8} \to \cfrac{4}{8} \to 0 \to 0 \cdots}$$
などです。
どちらも最終的に原点$${(0,0)}$$に到達します。
(b2)10進小数で分母が2のべき乗以外の有理数なら2進小数では循環小数になり、n周期点もしくは究極的なn周期点となります。
(例)$${\cfrac{1}{10}=(0.0 \dot{0} 01\dot{1})_2}$$
右辺を$${A}$$とおいて
$${A=(0.0\dot{0}01\dot{1})_2}$$
$${2A=(0.\dot{0}01\dot{1})_2}$$
$${2^{5}A=(0011.\dot{0}01\dot{1})_2}$$
引き算して
$${(2^5-2)A=(0011)_2=3}$$
$${A=\cfrac{1}{10}}$$
$${B}$$を作用させると
$${\cfrac{1}{10} \to \cfrac{2}{10} \to \cfrac{4}{10} \to \cfrac{8}{10}\to \cfrac{6}{10} \to \cfrac{2}{10}}$$
$${\cfrac{1}{10}}$$は循環節の長さが4の循環小数であるから$${B(x)}$$の究極的な4周期点となります。最終的に図7-3で$${1 \to 2\to 3\to 4 \to 1 \cdots}$$と循環します。
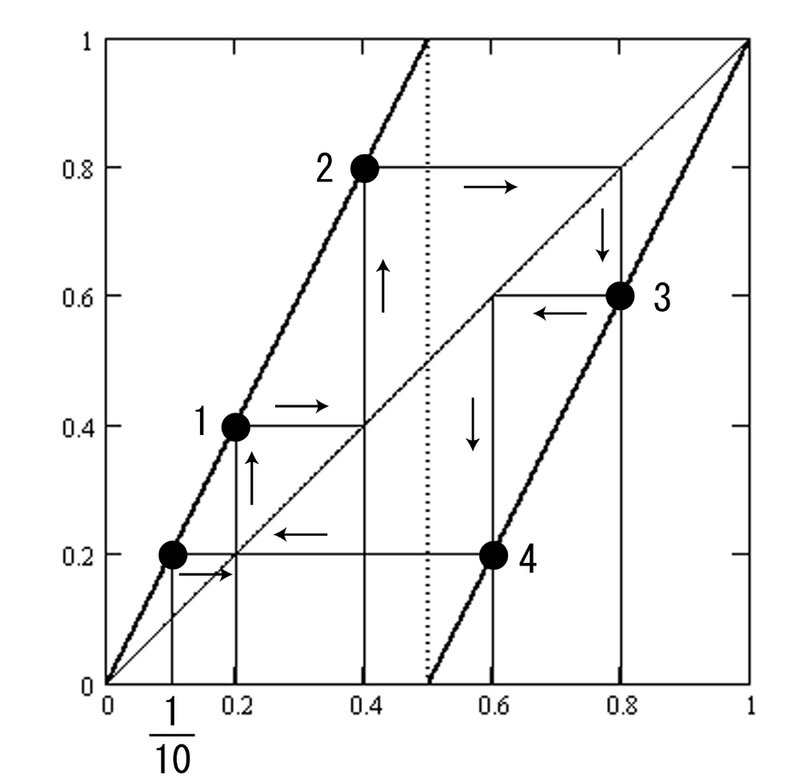
図7-4は2周期点のクモの巣グラフ図です。
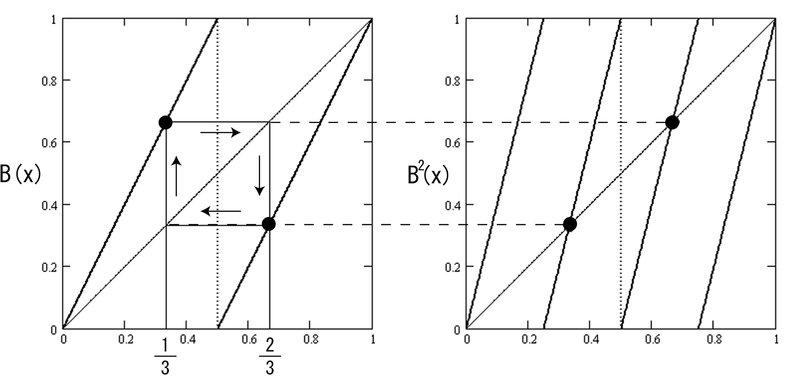
(b3)無理数は循環しない無限小数になり、非周期軌道になります。
ベルヌーイシフト写像の初期値が有限値か有理数か無理数かにより、
コラッツルールに従った数列では
(b1)は1に到達するに類似しています。
(b2)はある数字に戻ってきてしまう(ループする)に類似しています。
(b3)は無限回で、周期性もないし1にも到達しないに類似しています。
一般コラッツ空間の2進法解析でも、上手く0以上1未満になるような
写像を考え出してカオス力学手法が使えるようにすれば、何かしらの進展がみられるかもしれません、もしかしたら解けるかもしれません。ベルヌーイシフト写像はそのヒントになっています。
7.3 解明へと新分野
クリエータは自己紹介でも述べたように物性物理分野で今まで解析を行ってきました。整数論もカオス理論も本格的に勉強したわけではありません。今回の記事は高校数学で十分理解できます。その範囲で今回の新手法は解析できたわけですから、結果的に2種理論の導入部分がわかっているだけでよかったわけです。
解明となりますと、全部ではないにしてもカオス理論をより深く勉強していく必要があります。その道の専門分野の学者さんなら解いてしまうのではということも考えられます。そうは言いつつも新手法を公開しなければ、二番手になってしまう可能性もあるわけです。
CS空間では扱う数は無理数(循環しない無限小数)は扱っていません。
7.2の例のように無理数でなければ無限回数になることはないわけですが
カオス理論の一次元線形写像(係数有理数)では常識(?)であるならば(クリエータはカオス理論のプロではありませんので常識かどうかは定かではありませんが)、コラッツ予想でも無限回になることはないことは第6章時点で言えているのかもです、もしくは演習問題レベルかもしれません。
解析的整数論(第1章1.7)のように別分野で解くことにより新しい分野が開かれることがあります。今回の新手法もこれを元に将来新しい分野が開かれれば、解明よりもより価値あるものだったと思いたいですね。
記事内容や証明で「なるほど」とお感じになったら、評価の程よろしくお願いいたします。今後の解析の奮起につながります。
この記事が気に入ったらサポートをしてみませんか?
