New Method for Solving the Collatz Conjecture 5 with High-Prize Money
Chapter 4: Relationship between Odd Number Classification and S-Transformation (article 5)
Please read "Introduction to a New Method in Chapter 1 (article 1)"
before reading Chapter 4 (article 5).
Chapter 1 also posts links to each chapter.
When translating from Japanese to English, subtle nuances of the original articles may not be fully conveyed. If you would like to view the original Japanese articles, please see Chapter 1 of Japanese Article 1.
Summary Video of the New Method in English
4.1 Summary of Previous Chapters
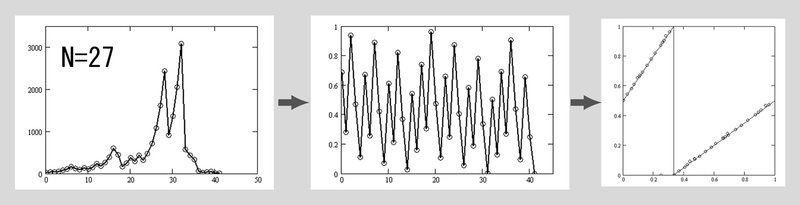
Figure 4-1 (left) shows a graph of the odd values of each step taken until reaching 1, tracking only odd numbers $${No}$$ with an initial value of 27 as an example. In Chapter 2, Sections 2.1 and 2.2, The equation for deriving the CS-vibration (middle figure) of this graph, in other words, the C-transformation $${\bm{c(No)}}$$ were introduced .
The CS-plot of all step points are shown to exist "close" to the CS-linear- equations (right figure).
Sections 2.3 further demonstrates that the CS-linear-equations (solid line in the right figure) is a function independent of the initial value $${No}$$. Moreover, it proves that for any initial value, all CS-plot points of all step points exist "close" to the CS-linear-equations (the larger the value, the closer it is to the line).
It was also explained that even numbers can be inevitably ignored in the world of $${c(No)}$$.
The new method article only tracks positive odd numbers $${No}$$. For example, $${13 \to 5 \to 1}$$ is counted as two steps. In a world that follows the Collatz rule (triple and add 1 for odd numbers, divide by 2 for even numbers), there are unique number sequences. For example, there are an infinite number of odd numbers that reach 1 in one step: $${1,5,21,85,341,\cdots}$$.
It was explained in Chapter 3 that any odd number $${m_o}$$ (excluding multiples of 3, since they never reach 1) has an infinite number of odd number sequences that reach it. This odd number sequence is defined as $${\bm{cs(m_o)}}$$. The above-mentioned odd number sequence is equivalent to $${cs(1)}$$.
CS-plot points after applying the C-transformation have both x-coordinates and y-coordinates in the range of 0 to 1 (see the right figure above).
The aim is to introduce the above-mentioned unique number sequences into this world by applying the C-transformation, $${c(No)}$$, and the
S-transformation, $${\bm{s(No)}}$$ defined below, to odd numbers $${No}$$.
This world will be referred to as the CS-space.
Chapter 4 is the chapter immediately preceding the method of placing
CS- plot points with arbitrary odd numbers $${No}$$ on the CS-linear- equation, not close to but perfectly. This chapter is not about simply placing them formally, but about deriving the relationship with the number sequence $${cs(m_o)}$$ unique to the Collatz conjecture.
The knowledge acquired up to Chapter 4 allows any positive odd number, including the intermediate odd numbers during the steps, to be plotted on the CS-linear-equation. This chapter plays a key role in the overall understanding of the new method.
The figure below illustrates an example of plot points and the CS-line (solid line) in the CS-space for the initial value of 27. All plot points are perfectly aligned on the CS-line. This is achieved by alternately combining the
C-transformation and S-transformation. Remarkably, all the number trees in the general Collatz space plot on these two lines in the CS space. The CS alternating combination is explained in Section 6.2.
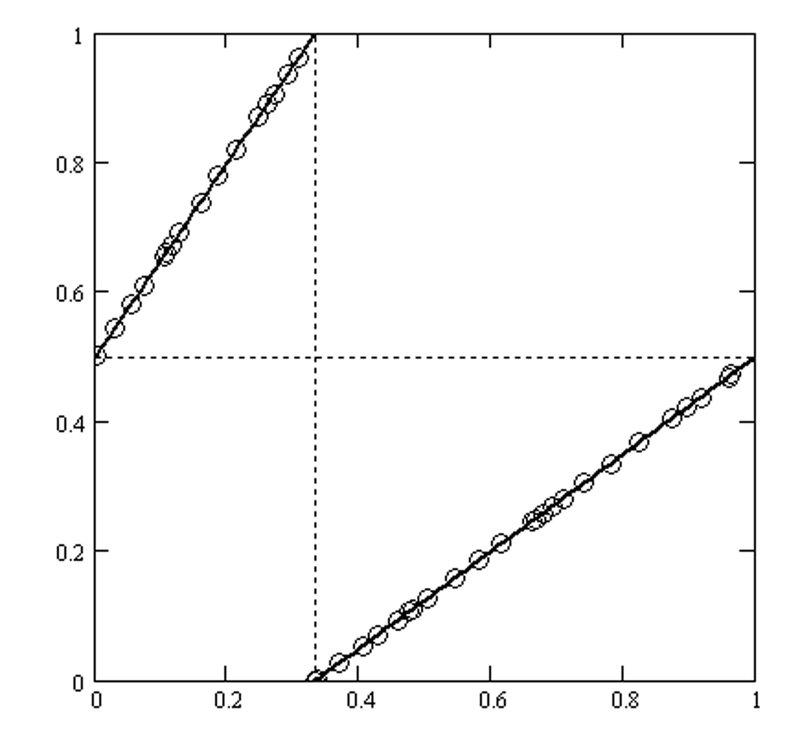
including odd numbers during the steps with an initial value of 27 on the CS-space.
(Regardless of the initial value, there will always be plot points on the CS line.)
Variables, Definitions, and Functions up to Chapter 4:
$${N}$$, $${No}$$,
total number of steps, step number, CS-vibration, C-transformation,
CS-plot, CS-linear-equations, 3C+1 transformation, 3S+1 transformation,
(general) Collatz space, CS-line, S-transformation, CS-space, t-tree,
type $${6t+5}$$, $${6t+1}$$, $${4t+3}$$, $${8t+1}$$, etc.
$${c(No)}$$, $${z_{s}}$$, $${f_{c}(x)}$$, $${f_{s}(x)}$$, distance$${D}$$,
$${Nc}$$, $${Ns}$$, $${m_o}$$, $${m_{c}}$$, $${m_{s}}$$, $${t_{c}}$$, $${t_{s}}$$, $${t}$$, $${cs(m_o)}$$, $${Mo}$$, $${s(Mo)}$$,
The new method is introduced in Articles 1-10 and Chapters 1-8.
The translation from Japanese to English has been completed for all articles, both free and paid. (April 2024)
4.2 Definition and Specific Example of S-Transformation
ここから先は
¥ 800
この記事が気に入ったらサポートをしてみませんか?
