New Method for Solving the Collatz Conjecture 9 with High-Prize Money
Please read "Introduction to a New Method in Chapter 1 (article 1)"
before reading Chapter 7 (article 9).
Chapter 1 also posts links to each chapter.
When translating from Japanese to English, subtle nuances of the original articles may not be fully conveyed. If you would like to view the original Japanese articles, please see Chapter 1 of Japanese Article 1.
Summary Video of the New Method in English
Chapter 7: Can the Collatz Conjecture be Solved? Maybe? Possibly?
7.1 Difficult to Solve out using Conventional Methods
C have been working on the Collatz conjecture for about a year and a half. C used to write calculations and summaries in 10 one-centimeter-thick handwritten notebooks. (C is me, Creator.)
When C reviewed them after a while, C could not remember what the calculations were for because C's handwriting was poor. Therefore, C used LaTeX to summarize them as needed. This allows C to review the analytical content at any time.
Before that, C was addicted to Monster Hunter and other games.
After learning about the world of unsolved historical problems, C became completely addicted to it (^^)
After summarizing, C has found that while it seems possible to solve the Collatz conjecture using an orthodox approach like that in Chapter 3, C hits a wall at the last few percent. C has tried various approaches, but all have hit a wall. This is not surprising, as professional and amateur mathematicians have been analyzing the problem for over 80 years, so it is natural that a general approach would not be able to break through its defenses.
There are some useful papers. For example, there is the paper introduced in the "Don't Laugh Math" program in Japan. It said, "Cornelius Everett's proof is short at 4 pages and does not use very advanced mathematics. It is an English paper, but please feel free to read it if you are interested."
https://www.sciencedirect.com/science/article/pii/0001870877900871
When considering all natural numbers as initial values and representing the values of intermediate steps with 1 and 0 according to the rules, A certain harmony, or a wave-like pattern of 1s and 0s, can be seen in all natural numbers. This is a must-read for readers who are working on the Collatz conjecture. Although it is only two and a half pages long in the first half, it is difficult to understand just by reading it because there are few concrete examples. C wrote it down in a handwritten notebook and verified it on a computer. The regularity is surprising.
The latter part concludes that the Collatz conjecture is correct for "almost" all numbers probabilistically, based on the assumption that all numbers eventually have an equal number of 1s and 0s. There is only one reference, which seems to describe the content of the probabilistic method based on it. Since it is impossible to reach a complete proof in probability theory, the conjecture is stated to be correct for "most" numbers.
Some online articles claim that it has been proven, which may increase their access count. However, there are many articles that question why this is considered a proof.
Even if it may be acceptable at the article stage, but there are also cases where it is claimed to have been proven even though probability theory is used in preprints. The number of accesses will certainly increase. However, it is not being cited by other papers. It is also strange to cite a preprint or paper that claims to have proven the Collatz conjecture in the literature of other preprints and papers on the Collatz conjecture.
Although I have not read Terence Tao's preprints or papers, they use probability theory and he himself states that they are far from a complete proof (Chapter 1). They are often cited as references. He is a genius, so that is also a reason why they are cited.
Fermat's Last Theorem remained unsolved for over 360 years, until Andrew Wiles proved the Taniyama-Shimura conjecture and solved it in 1995.
The four color theorem was proposed by French mathematician François Guthrie in 1852. A proof and verification using a computer program was conducted from 1976 to 2004, and the four color theorem is now considered solved (Wikipedia).
We cannot wait for things like the Taniyama-Shimura conjecture to be proven or for computers to develop further, and so on. By the time that happens, we will no longer be in this world.
While direct approaches or conventional method can yield promising results, they ultimately fall short of a complete solution. This is evidenced by the long history of these problems remaining unsolved. While it is possible that they will be solved someday, we working on them naturally want to solve them during their lifetimes. we do not want to pass the problem on to the next generation.
In that case, it is also a viable option to seek solutions in another field with a well-established theoretical framework. Grigori Perelman solved the Poincaré conjecture using physics, rather than the conventional approach.
This new method has successfully transformed a proposition equivalent to the Collatz conjecture in the general Collatz space into a proposition on the CS- space, where chaos dynamics methods with an established theoretical framework (which is still under development) can be applied.
This is particularly significant because it involves a one-dimensional linear map between 0 and 1, which is considered the introductory part of chaos dynamics.
Now
Can it be solved using chaos theory?
7.2 Bernoulli Shift (Binary Transformation) Mapping
There are also people working on the Collatz conjecture using binary numbers online. Therefore, I will introduce the Bernoulli shift (binary transformation) map, which is a chaotic dynamics map. It is not directly related to the Collatz conjecture, but it is interesting to see the similarity between it and a simple linear map.
$${ 2x (A:0 \le x < 1/2)}$$
$${(7.1) B(x)=}$$
$${ 2x-1 (B:1/2 \le x < 1)}$$
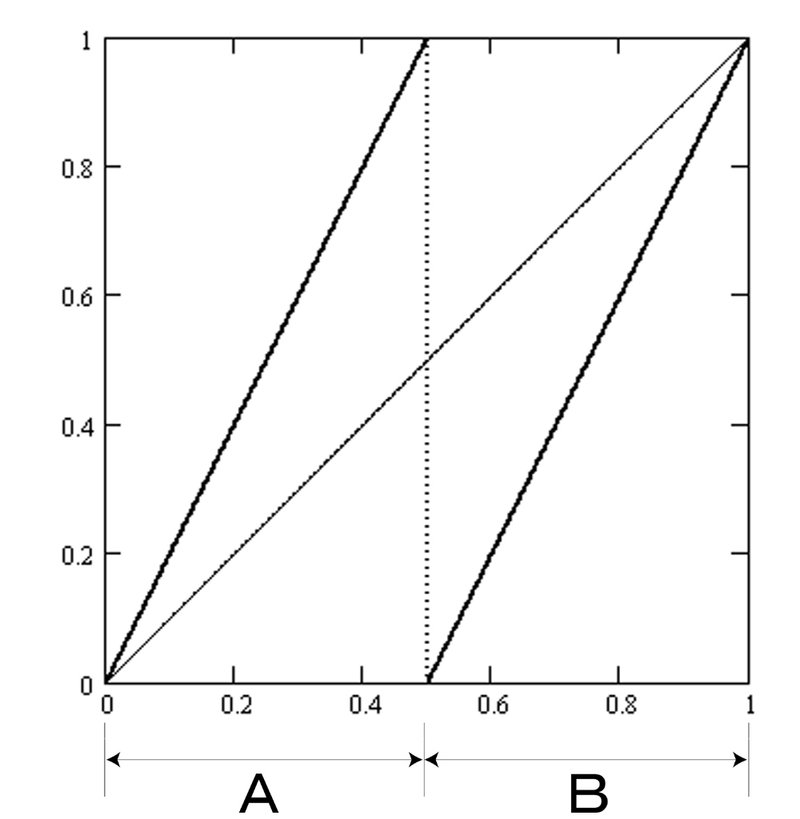
Let x be a real number such that 0≤x<1. x can be represented in binary as follows:
$${x=(0.x_1x_2\cdots x_n \cdots)_2}$$
where each $${x_n}$$ is either $${0}$$ or $${1}$$.
In decimal, $${x_n}$$ can be expressed as follows:
$${x=\cfrac{x_1}{2^1}+\cfrac{x_2}{2^2}+\cdots+\cfrac{x_n}{2^n}+\cdots}$$
The expression $${x=(0.x_1x_2\cdots x_n \cdots)_2}$$ can be classified based on the value of the first digit after the decimal point, $${x_1}$$, either 0 or 1.
(a1) Case where $${x_1=0}$$:
If $${x_1=0}$$, then $${x<\cfrac{1}{2}}$$. Therefore,
$${B(x)=2x=2\left(\cfrac{0}{2^1}+\cfrac{x_2}{2^2}+\cdots+\cfrac{x_n}{2^n}+\cdots\right)}$$
$${ =\cfrac{x_2}{2^1}+\cfrac{x_3}{2^2}+\cdots+\cfrac{x_{n+1}}{2^{n}}+\cdots =(0.x_2x_3\cdots x_{n+1} \cdots)_2}$$
(a2) Case where $${x_1=1}$$:
If $${x_1=1}$$, then $${\cfrac{1}{2} \le x < 1}$$. Therefore,
$${B(x)=2x-1=2\left(\cfrac{1}{2^1}+\cfrac{x_2}{2^2}+\cdots+\cfrac{x_n}{2^n}+\cdots\right)-1}$$
$${ =\cfrac{x_2}{2^1}+\cfrac{x_3}{2^2}+\cdots+\cfrac{x_{n+1}}{2^{n}}+\cdots =(0.x_2x_3\cdots x_{n+1} \cdots)_2}$$
From (a1) and (a2), binary conversion can be viewed as a shift operation that shifts the binary representation $${\bm{x=(0.x_1x_2\cdots x_n \cdots)_2}}$$ one bit to the left.
$${B(x)=(0.x_2x_3\cdots x_{n+1} \cdots)_2}$$
$${B^2(x)=(0.x_3x_4\cdots x_{n+2} \cdots)_2}$$
$${B^3(x)=(0.x_4x_5\cdots x_{n+3} \cdots)_2}$$
$${B^n(x)=(0.x_{n+1}x_{n+2}\cdots x_{2n} \cdots)_2}$$
The following examines the relationship between the Bernoulli shift map and finite decimal values, rational numbers, irrational numbers, and so on.
(b1) If the denominator of a decimal fraction is a power of 2, the binary
representation becomes a finite value and eventually reaches the origin
(0,0).
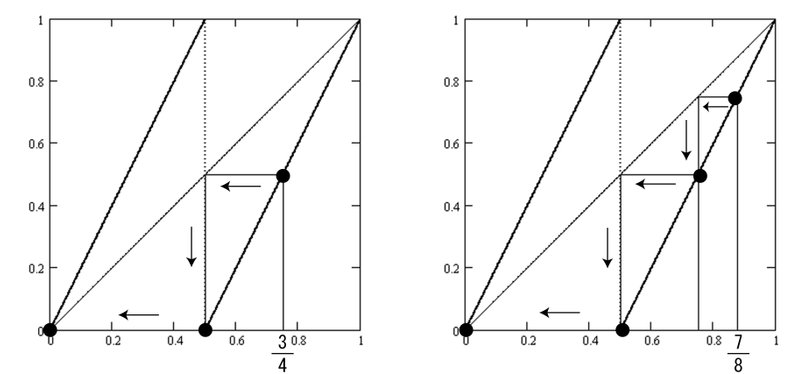
$${\cfrac{3}{4}=\cfrac{1}{2^1}+\cfrac{1}{2^2}=(0.11)_2}$$
Under the action of B, $${\cfrac{3}{4} \to \cfrac{2}{4} \to 0 \to 0 \cdots}$$
$${\cfrac{7}{8}=\cfrac{4+2+1}{8}=\cfrac{1}{2^1}+\cfrac{1}{2^2}+\cfrac{1}{2^3}=(0.111)_2}$$
Under the action of B, $${\cfrac{7}{8} \to \cfrac{6}{8} \to \cfrac{4}{8} \to 0 \to 0 \cdots}$$
, and so on.
Both eventually reach the origin (0,0).
(b2) For rational numbers with a denominator that is not a power of 2 in
decimal form, it becomes a repeating decimal in binary form, and is
either an n-periodic point or an eventually n-periodic point.
(ex.)$${\cfrac{1}{10}=(0.0 \dot{0} 01\dot{1})_2}$$
Let the right-hand side be A,
$${A=(0.0\dot{0}01\dot{1})_2}$$
$${2A=(0.\dot{0}01\dot{1})_2}$$
$${2^{5}A=(0011.\dot{0}01\dot{1})_2}$$
by subtraction,
$${(2^5-2)A=(0011)_2=3}$$
$${A=\cfrac{1}{10}}$$
applying B,
$${\cfrac{1}{10} \to \cfrac{2}{10} \to \cfrac{4}{10} \to \cfrac{8}{10}\to \cfrac{6}{10} \to \cfrac{2}{10}}$$
Since $${\cfrac{1}{10}}$$ is a repeating decimal with a period length of 4, it becomes an eventually 4-periodic point of $${B(x)}$$. Eventually, it cycles as $${1 \to 2\to 3\to 4 \to 1 \cdots}$$ in Figure 7-3.
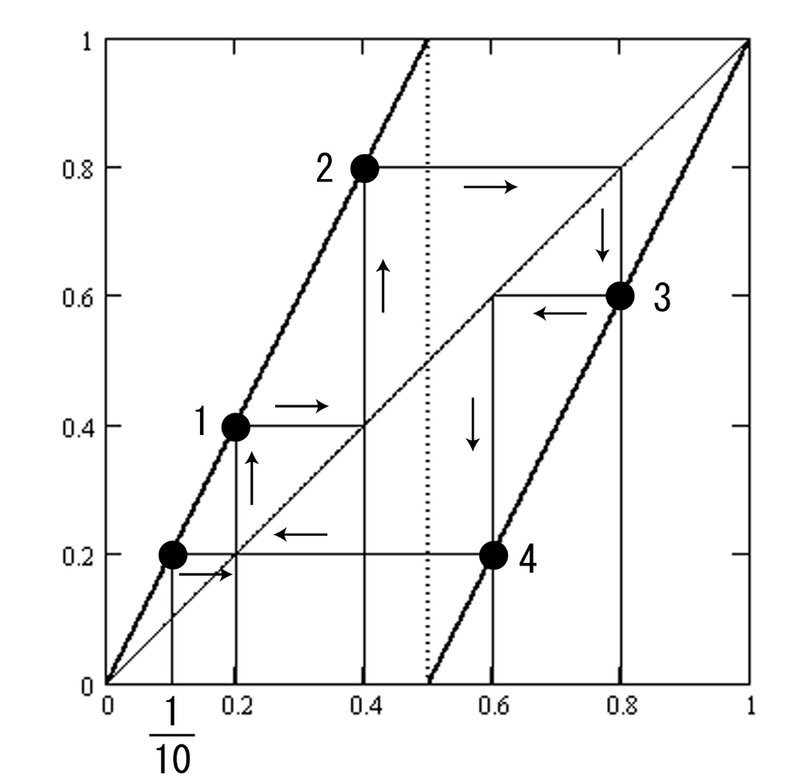
Figure 7-4 shows a cobweb diagram of a 2-periodic point.
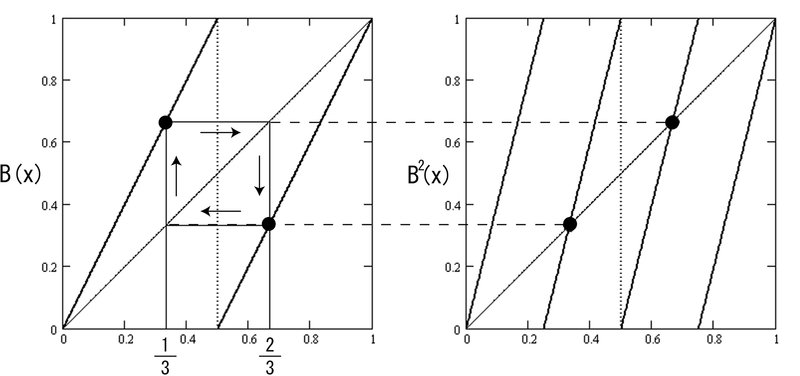
(b3) Irrational numbers become non-repeating infinite decimals and non- periodic orbits.
Depending on whether the initial value of the Bernoulli shift map is a finite value, a rational number, or an irrational number, the sequence following the Collatz rule:
(b1) is similar to reaching 1.
(b2) is similar to returning to a certain number (looping).
(b3) is similar to continuing infinitely without periodicity or reaching 1.
In the binary analysis of the general Collatz space, If a mapping can be devised that successfully produces values between 0 and 1, and chaos theory techniques can be applied, then some progress may be observed, and it may even be possible to solve the problem.
The Bernoulli shift map serves as a hint in this regard.
7.3 Towards Elucidation and a New Field
C has conducted analysis in the field of materials physics, as mentioned in the introduction. C has not strictly studied either number theory or chaos theory. This article can be fully understood with high school mathematics. Since the new method could be analyzed within this scope, it was ultimately sufficient to simply understand the introductory part of the two-species theory.
To solve it, it is necessary to study chaos theory more deeply, even if not completely. It is also conceivable that a scholar specializing in the field could solve it. However, if C do not publish the new method, C may end up being the second best.
The numbers used in CS space do not deal with irrational numbers (non-repeating decimals).
In the case of Example 7.2, if the number is not irrational, it does not become infinite. However, if this is not only true for this example, but also a common sense ( ? : C is not an expert in chaos theory, so it is not clear whether this is a common sense or not.) in the context of one-dimensional linear map with rational coefficients in chaos theory, then it may be possible to say in Chapter 6 that the Collatz conjecture will not become infinite, or it may be a level of exercise problem.
Just as in analytic number theory (Chapter 1.7), solving a problem in a different field can sometimes lead to the discovery of a new field. If this new method can lead to the discovery of a new field in the future, C would like to think that it was something more valuable than solving the Collatz conjecture.
If you find the content of this article to be "I see" , please consider giving it a good rating. Your feedback will motivate me to continue my analysis in the future.
この記事が気に入ったらサポートをしてみませんか?
