３次方程式に解の公式が存在する理由（前編）

　５分間の休憩が終わり、森田君はホワイトボードに向かった。
「前半は解の置換という観点で、２次方程式に解の公式が存在する理由について述べました。後半は３次方程式について考えます。３次方程式の場合も同じようなステップで説明できます。内容が抽象的になりますが、これまでの授業で計算はしっかりとやってきたので、必要に応じて簡単に復習していきます。
　まずは３次方程式の一般型 $${ax^3+bx^2+cx+d=0}$$ の両辺を $${a(\ne0)}$$ で割って
　$${x^3+\dfrac{b}{a}x^2+\dfrac{c}{a}x+\dfrac{c}{a}=0}$$
これを $${x=y-\dfrac{b}{3a}}$$ と置き換えることによって
　$${y^3+px+q=0}$$
ただし
　$${p=-\dfrac{1}{3}\left(\dfrac{b}{a}\right)^{2}+\dfrac{c}{a}}$$
　$${q=\dfrac{2}{27}\left(\dfrac{b}{a}\right)^{3}-\dfrac{1}{3}\left(\dfrac{b}{a}\right)\left(\dfrac{c}{a}\right)+\dfrac{d}{a}}$$
と、より簡単な $${y}$$ についての３次方程式に変形できます。この変形のことを『チルンハウス変換』といいました。この $${y^3+px+q=0}$$ の３つの解を $${\alpha,  \beta,  \gamma}$$ と置きます」
「さて森田君、核心に入る前に改めて『３次置換』、『遇置換』、『奇置換』、あとそれらを『互換』で表したり、また「三角形の回転」として視覚化できることは大丈夫かな？」
　まだまだ小学５年生の森田君。「確認します」とここはしっかりとノートを復習する。

---

＜３次置換について（復習）＞
　一般に文字や対象を入れ替えたり並べ替えたりすることを『置換』という。２つの文字 $${\alpha,  \beta}$$ の置換を『２次置換』、３つの文字 $${\alpha,  \beta,  \gamma}$$ の置換を『３次置換』、一般に $${n}$$ 個の文字の置換を『$${\boldsymbol{n}}$$ 次置換』という。先ほどやった２次方程式の２つの解 $${\alpha,  \beta}$$ の置換は２次置換、これからやる３次方程式の３つの解 $${\alpha,  \beta,  \gamma}$$ の置換は３次置換である。
　$${\alpha,  \beta,  \gamma}$$ の３次置換は、以下の６つのみである。２次置換と同様にカッコ（　　）の中の文字は、上から下に置換されると見ればよい。

➀　$${\alpha}$$ を $${\alpha}$$ に、$${\beta}$$ を $${\beta}$$ に、$${\gamma}$$ を $${\gamma}$$ に、つまりそのままで変わらない置換、すなわち

$$
\begin{align*}
\alpha\longrightarrow \alpha\\
\beta\longrightarrow \beta\\
\gamma\longrightarrow \gamma
\end{align*}
\hspace{12pt}を\hspace{10pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
$$

と表す。このように何も変化しない置換を『恒等置換』という。この置換は下図のように、回転しない三角形とみることができる。

②　$${\alpha}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に置き換える置換、すなわち

$$
\begin{align*}
\alpha\longrightarrow\gamma\\
\beta\longrightarrow\alpha\\
\gamma\longrightarrow\beta
\end{align*}
\hspace{12pt}を\hspace{10pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
$$

と表す。$${\alpha → \gamma → \beta → \alpha}$$ と巡回する置換なので、これを『巡回置換』という。この置換は下図のように、三角形の反時計回り１２０°の回転とみることができる。

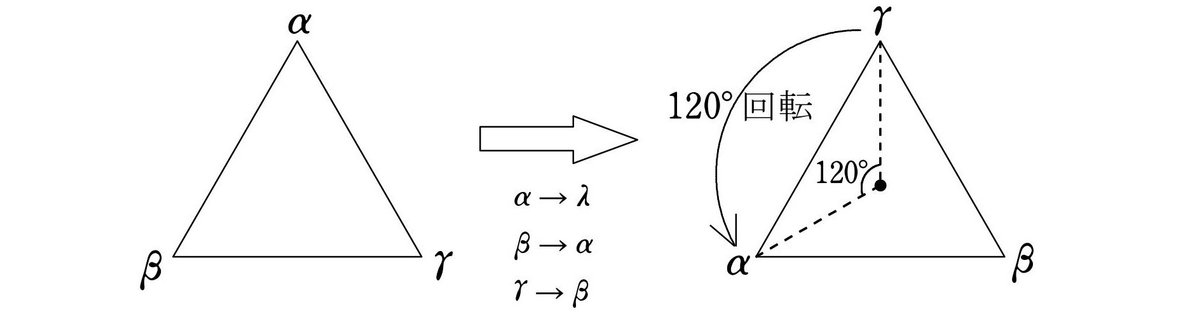
この回転によって $${\alpha}$$ の地点が $${\gamma}$$、$${\gamma}$$ の地点が $${\beta}$$、 $${\beta}$$ の地点が $${\alpha}$$ に置き換わるので、$${\alpha → \gamma → \beta → \alpha}$$ の三角形の回転とみることができる。

③　$${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\alpha}$$ に置き換える置換、すなわち

$$
\begin{align*}
\alpha\longrightarrow \beta\\
\beta\longrightarrow \gamma\\
\gamma\longrightarrow \alpha
\end{align*}
\hspace{12pt}を\hspace{10pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
$$

と表す。$${\alpha → \beta → \gamma → \alpha}$$ と巡回する置換なので、これも『巡回置換』となる。この置換は下図のように、三角形の反時計回り２４０°の回転とみることができる。

この回転によって $${\alpha}$$ の地点が $${\beta}$$、$${\beta}$$ の地点が $${\gamma}$$、 $${\gamma}$$ の地点が $${\alpha}$$ に置き換わるので、$${\alpha → \beta → \gamma → \alpha}$$ の三角形の回転とみることができる。

④　$${\alpha}$$ はそのままで、$${\beta}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\beta}$$ に置き換える置換、すなわち

$$
\begin{align*}
\alpha\longrightarrow\alpha\\
\beta\longrightarrow\gamma\\
\gamma\longrightarrow\beta
\end{align*}
\hspace{14pt}を\hspace{10pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
$$

と表す。この置換は $${\alpha}$$ はそのままで、$${\beta}$$ と $${\gamma}$$ を入れ替える置換なので

$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
$$

と簡単に表すことがある。この $${(\beta     \gamma)}$$ を「互いに交換する」という意味で『互換』という。なお、互換は「２つの解の巡回置換」とみることもできる。この置換は下図のように、$${\alpha}$$ を通る対称軸 $${l}$$ についての折り返しとみることができる。

➄　$${\alpha}$$ を $${\gamma}$$ に、$${\beta}$$ はそのままで、$${\gamma}$$ を $${\alpha}$$ に置き換える置換、すなわち

$$
\begin{align*}
\alpha\longrightarrow\gamma\\
\beta\longrightarrow\beta\\
\gamma\longrightarrow\alpha
\end{align*}
\hspace{12pt}を\hspace{10pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
$$

この置換は $${\beta}$$ はそのままで、$${\alpha}$$ と $${\gamma}$$ を入れ替える置換なので

$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}
$$

と『互換』で表すことがある。この置換は下図のように、$${\beta}$$ を通る対称軸 $${m}$$ についての折り返しとみることができる。

⑥　$${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に、$${\gamma}$$ は変化しない置換、すなわち

$$
\begin{align*}
\alpha\longrightarrow\beta\\
\beta\longrightarrow\alpha\\
\gamma\longrightarrow\gamma
\end{align*}
\hspace{12pt}を\hspace{10pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
$$

この置換は $${\gamma}$$ はそのままで、$${\alpha}$$ と $${\beta}$$ を入れ替える置換なので

$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
$$

と『互換』で表すことがある。この置換は下図のように、$${\gamma}$$ を通る対称軸 $${n}$$ についての折り返しとみることができる。

　なお恒等置換➀と、巡回置換②、③についても互換で表すこと、正確に言うと「互角の積」で表すことができる。以下まとめして、すべての３次置換①～➅について、互換（または互換の積）で表すと次のようになる。

＜３次置換のすべての互換表示（復習）＞

➀について

$$
\begin{align*}
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
\end{align*}
$$

同じ入れ換えを２回連続で行っているので、もとに戻るのは当たり前だが、こういうケースも考える。互換の表記は必ずしも１通りとは限らず、上記のように複数の表し方がありうる。
　例として一番上の互換の積だけ、三角形での互換の例をあげる。 互換 $${(\alpha     \beta)}$$ を作用させてから再び  $${(\alpha     \beta)}$$ を作用させると、もとの置換➀と同じ結果となる。

②について

$$
\begin{align*}
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\end{align*}
$$

なお互換の順番は、左から順に作用させていくと定義する。一番上の例でいうと $${(\beta     \gamma)}$$ を作用させてから、次に $${(\gamma     \alpha)}$$ を作用させる、つまり

$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=
\underrightarrow{\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}}
$$

と矢印の順に、前の方から作用させる。テキストによっては後ろからと逆に定義している場合もあるが、そのテキストにおいて一貫していれば問題ない。やはりここでも互換の表記は必ずしも１通りとは限らず、上記のように複数の表し方がありうる。
　上記の３つの互換の積について、上から順に三角形での例をあげる。１番上の互換の積について、$${(\beta     \gamma)}$$ のあとに $${(\gamma     \alpha)}$$ を作用させると、もとの置換②と同じ結果となる。

③について

$$
\begin{align*}
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
&\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}
\end{align*}
$$

やはりここでも互換の表記は必ずしも１通りとは限らず、上記のように複数の表し方がありうる。
　上記の３つの互換の積について、上から順に三角形での例をあげる。１番上の互換の積について、$${(\beta     \gamma)}$$ のあとに $${(\alpha     \beta)}$$ を作用させると、もとの置換➂と同じ結果となる。

④について

$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
$$

これは、$${\alpha}$$ を通る対称軸 $${l}$$ についての折り返しとみることができる。

⑤について

$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}
$$

これは、$${\beta}$$ を通る対称軸 $${m}$$ についての折り返しとみることができる。

⑥について

$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
$$

これは、$${\gamma}$$ を通る対称軸 $${n}$$ についての折り返しとみることができる。

　ここで用語の定義をする。２つ、４つなど、偶数個の互換で表せる置換を『遇置換』、１つ、３つなど、奇数個の互換の積で表せる置換を『奇置換』という。何も変化しない恒等置換は２つの互換の積で表されるので遇置換である。
　ここで $${n}$$ 次置換について、一般に次の定理が成り立つ（証明は略）。

＜『$${\boldsymbol{n}}$$ 次置換』についての定理（復習）＞

（定理Ⅰ）すべての $${n}$$ 次置換は、１つの互換、または複数の互換の積で表すことができる。
　例えば先ほどの３次置換①～➅について、①～③は２つの互換の積、④～⑥は１つの互換で表される。

（定理Ⅱ）ある $${n}$$ 次置換について、その置換が遇置換になるか、奇置換になるかはあらかじめ決まっている。つまり、ある $${n}$$ 次置換が、互換の選び方によって遇置換になったり奇置換になったりすることはない。
　例えば先ほどの３次置換①～➅について、①～③は必ず遇置換で奇置換になることはなく、④～➅は必ず奇置換で遇置換になることはない。なお、①～③は複数ある互換の積のうち、代表で１つの互換の積を選んだ。

$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}\\
\\
②\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}\\
\\
③\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}遇置換\\
\\
&\begin{rcases}
④\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
⑤\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}\\
\\
⑥\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}奇置換
\end{align*}
$$

（定理Ⅲ）$${n}$$ 次置換について、遇置換と奇置換に分けたときに、そのときの遇置換と奇置換の個数はもとの置換の２分の１で、互いに同じ個数となる。
　例えば先ほどの６つの３次置換について、遇置換は①～③の３つ、奇置換は④～➅の３つで、ちょうど半分ずつ、同じ数ずつ振り分けられる。例えば遇置換が４つ、奇置換が２つのようにはならず、遇置換と奇置換の個数はきっちりと半分ずつに分かれる。

$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}\\
\\
②\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}\\
\\
③\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}３通り\\
\\
&\begin{rcases}
④\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
⑤\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}\\
\\
⑥\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}３通り
\end{align*}
$$

---

　しっかりと基本を確認をした森田君は、すくっと立ち上がりホワイトボードに向かった。
「まずは先ほどやった２次方程式のときと同じように、３次方程式についても、次の条件Ⅰを満たす「解の式 $${X}$$」を考えます。

$${\boldsymbol{X}}$$ の条件Ⅰ
　『$${X}$$ は対称式ではないが、$${X^2}$$ は対称式である。』
詳しく言うと
　『$${X}$$ は３次置換で対称性がこわれているが、$${X^2}$$ では３次置換で対称性を保つ。』
　なお言葉として、「ある置換で式が変化する」ことを「対称性がこわれている」、「ある置換で式が変化しない」ことを「対称性を保つ」などと表現することがあります。
（例）
　差積 $${(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$ は奇置換では対称性がこわれているが、遇置換では対称性を保つ。

　さて２次方程式では、この条件Ⅰを満たす「解の式 $${X}$$」は２つの解の差積
　$${X_2=\alpha-\beta}$$
でしたが、これから議論する３次方程式では、３つの解の差積
　$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
となります。なお $${X}$$ の記号について、２次方程式の２つの解の差積は $${X_2}$$、３次方程式の３つの解の差積は $${X_3}$$ と今後は記述していきます。すると、４次方程式の４つの解の差積は $${X_4}$$、５次方程式の５つの解の差積は $${X_5}$$、$${\cdots}$$ と区別して表記が可能です。
　さて３つの解の差積
　$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
について、『$${X_3}$$ は３次置換で対称性がこわれているが、$${(X_3)^2}$$ では３次置換で対称性を保つ。』ことを改めて復習しておきます」

---

＜$${\boldsymbol{X_3}}$$ は３次置換で対称性がこわれていること（復習）＞

①　$${\dbinom{\alpha       \beta       \gamma}{\alpha       \beta       \gamma}}$$ について。同じ文字同士を置き換える置換なので変化しない。

$$
\begin{align*}
&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{2pt}\downarrow\hspace{13pt}\downarrow\hspace{9pt}\downarrow\hspace{14pt}\downarrow \hspace{8pt}\downarrow\hspace{13pt}\downarrow\\
\longrightarrow\,&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)  \Leftarrow 変化しない
\end{align*}
$$

②　$${\dbinom{\alpha       \beta       \gamma}{\gamma       \alpha       \beta}}$$ について。$${\alpha}$$ を $${\gamma}$$ に、$${\beta}$$ を $${\alpha}$$ に、$${\gamma}$$ を $${\beta}$$ に置き換える置換なので

$$
\begin{align*}
&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{2pt}\downarrow\hspace{13pt}\downarrow\hspace{9pt}\downarrow\hspace{14pt}\downarrow \hspace{9pt}\downarrow\hspace{13pt}\downarrow\\
\longrightarrow\,&(\gamma-\alpha)(\alpha-\beta)(\beta-\gamma)\\
=\,&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)  \Leftarrow 変化しない
\end{align*}
$$

これは、カッコ (　　) の順番が入れ替わるだけなので、もとの式と変わらない。

③　$${\dbinom{\alpha       \beta       \gamma}{\beta       \gamma       \alpha}}$$ について。$${\alpha}$$ は $${\beta}$$ に、$${\beta}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\alpha}$$ に置き換える置換なので

$$
\begin{align*}
&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{2pt}\downarrow\hspace{13pt}\downarrow\hspace{9pt}\downarrow\hspace{14pt}\downarrow \hspace{9pt}\downarrow\hspace{13pt}\downarrow\\
\longrightarrow\,&(\beta-\gamma)(\gamma-\alpha)(\alpha-\beta)\\
=\,&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)  \Leftarrow 変化しない
\end{align*}
$$

これも、カッコ (　　) の順番が入れ替わるだけなので、もとの式と変わらない。

④　$${\dbinom{\alpha       \beta       \gamma}{\alpha       \gamma       \beta}}$$ について。$${\alpha}$$ はそのままで、$${\beta}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\beta}$$ に置き換える置換なので

$$
\begin{align*}
&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{20pt}\downarrow\hspace{9pt}\downarrow\hspace{14pt}\downarrow\hspace{9pt}\downarrow\\
\longrightarrow\,&(\underline{\alpha-\gamma})(\gamma-\beta)(\underline{\underline{\beta-\alpha}})\\
=\,&(\underline{\underline{\beta-\alpha}})(\gamma-\beta)(\underline{\alpha-\gamma})  \Leftarrow (　　)  を入れ替えた\\
=\,&(-\alpha+\beta)(-\beta+\gamma)(-\gamma+\alpha)\\
=\,&\{-(\alpha-\beta)\}\{-(\beta-\gamma)\}\{-(\gamma-\alpha)\}\\
=\,&(-1)^3(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
=\,&-(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)  \Leftarrow -1  倍と変化する
\end{align*}
$$

この場合は $${-1}$$ 倍と変化する。

⑤　$${\dbinom{\alpha       \beta       \gamma}{\gamma       \beta       \alpha}}$$ について。$${\beta}$$ はそのままで、$${\alpha}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\alpha}$$ に置き換える置換なので

$$
\begin{align*}
&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{2pt}\downarrow\hspace{46pt}\downarrow\hspace{8pt}\downarrow\hspace{14pt}\downarrow\\
\longrightarrow\,&(\underline{\gamma-\beta})(\underline{\underline{\beta-\alpha}})(\alpha-\gamma)\\
=\,&(\underline{\underline{\beta-\alpha}})(\underline{\gamma-\beta})(\alpha-\gamma)  \Leftarrow (　　)  を入れ替えた\\
=\,&(-\alpha+\beta)(-\beta+\gamma)(-\gamma+\alpha)\\
=\,&\{-(\alpha-\beta)\}\{-(\beta-\gamma)\}\{-(\gamma-\alpha)\}\\
=\,&(-1)^3(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
=\,&-(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)  \Leftarrow -1  倍と変化する
\end{align*}
$$

この場合も $${-1}$$ 倍と変化する。

⑥　$${\dbinom{\alpha       \beta       \gamma}{\beta       \alpha       \gamma}}$$ について。$${\gamma}$$ はそのままで、$${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に置き換える置換なので

$$
\begin{align*}
&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{2pt}\downarrow\hspace{14pt}\downarrow\hspace{8pt}\downarrow\hspace{46pt}\downarrow\\
\longrightarrow\,&(\beta-\alpha)(\underline{\alpha-\gamma})(\underline{\underline{\gamma-\beta}})\\
=\,&(\beta-\alpha)(\underline{\underline{\gamma-\beta}})(\underline{\alpha-\gamma})  \Leftarrow (　　)  を入れ替えた\\
=\,&(-\alpha+\beta)(-\beta+\gamma)(-\gamma+\alpha)\\
=\,&\{-(\alpha-\beta)\}\{-(\beta-\gamma)\}\{-(\gamma-\alpha)\}\\
=\,&(-1)^3(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
=\,&-(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)  \Leftarrow -1  倍と変化する
\end{align*}
$$

この場合も $${-1}$$ 倍と変化する。
　④～➅のように、１つの互換だけで表される奇置換では $${-1}$$ 倍と変化する。
　以上をまとめると、①～③の遇置換では $${(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$ は変化しない。

$$
\begin{rcases}
➀\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}\\
\\
②\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}\\
\\
③\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
\end{rcases}
\hspace{8pt}では\hspace{8pt}
\begin{align*}
&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\longrightarrow (\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{7pt}\Rightarrow \boldsymbol{\small 変化しない}
\end{align*}
$$

一方④～➅の奇置換では、$${(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$ は $${-1}$$ 倍と変化する。

$$
\begin{rcases}
④\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}\\
\\
➄\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}\\
\\
➅\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
\end{rcases}
\hspace{8pt}では\hspace{8pt}
\begin{align*}
&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\longrightarrow -(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{7pt}\Rightarrow \boldsymbol{\small -1  倍と変化する}
\end{align*}
$$

つまり $${X_3}$$ は遇置換では対称性を保っているが、奇置換では対称性がこわれているので、３次置換そのものでは対称性がこわれている。

　では次に、差積の２乗
　$${(X_3)^2=\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}$$
に①～➅の３次置換を作用させる。

＜$${\boldsymbol{(X_3)^2}}$$ は３次置換で対称性を保つこと（復習）＞

　①～③はもともと変化しないので、２乗しても変化しない。

$$
\begin{rcases}
➀\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}\\
\\
②\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}\\
\\
③\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
\end{rcases}
\hspace{8pt}では\hspace{8pt}
\begin{align*}
&\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2\\
&\longrightarrow\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2\\
&\hspace{7pt}\Rightarrow\boldsymbol{\small 変化しない}
\end{align*}
$$

④～➅は、$${-1}$$ 倍の $${2}$$ 乗は $${1}$$ 倍なので変化しない。

$$
\begin{rcases}
④\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}\\
\\
➄\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}\\
\\
➅\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
\end{rcases}
\hspace{8pt}では\hspace{8pt}
\begin{align*}
&\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2\\
&\longrightarrow \{-(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2\\
&\hspace{10pt}=(-1)^2\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2\\
&\hspace{10pt}=\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2\\
&\hspace{9pt}\Rightarrow\boldsymbol{\small 変化しない}
\end{align*}
$$

すなわち、①～➅のすべての３次置換を作用させても変化しないので
　$${(X_3)^2=\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}$$
は対称式となる。

$$
\begin{rcases}
➀\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}\\
\\
②\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}\\
\\
③\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}\\
\\
④\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}\\
\\
➄\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}\\
\\
➅\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
\end{rcases}
\hspace{8pt}では\hspace{8pt}
\begin{align*}
&{\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}}^2\\
&\longrightarrow {\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}}^2\\
&\hspace{7pt}\Rightarrow\boldsymbol{\small 変化しない}
\end{align*}
$$

---

「以上より、解の差積
　$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
は、先に述べた「解の式 $${X}$$」の条件Ⅰ

『$${X}$$ は３次置換で対称性がこわれているが、$${X^2}$$ では３次置換で対称性を保つ。』

を満たしています。２次方程式ではこの「差積」を考えることによって解の公式を導き出すことができましたが、３次方程式はここで終わりではありません。
　$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
は３次置換で対称性がこわれているとはいえ、まだ３つの遇置換➀～③で対称性が保たれているからです。

$$
\begin{rcases}
➀\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}\\
\\
②\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}\\
\\
③\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
\end{rcases}
\hspace{8pt}では\hspace{8pt}
\begin{align*}
&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\longrightarrow (\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{7pt}\Rightarrow \boldsymbol{\small 変化しない（対称性は保たれている）}\hspace{5pt}
\end{align*}
$$

$$
\begin{rcases}
④\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}\\
\\
➄\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}\\
\\
➅\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
\end{rcases}
\hspace{8pt}では\hspace{8pt}
\begin{align*}
&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\longrightarrow -(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{7pt}\Rightarrow \boldsymbol{\small -1  倍と変化（対称性はこわれている）}
\end{align*}
$$

先ほどやったように２次方程式では、差積の２乗
　$${(X_2)^2={(\alpha-\beta)}^2}$$
は対称式、つまり２次置換で対称性を保っているが、差積そのもの
　$${X_2=\alpha-\beta}$$
を変化させないで対称性を保つ置換は恒等置換のみでした。それによって
　$${X_2=\alpha-\beta}$$
と同等の対称性をもつ、恒等置換でのみ対称性を保つ $${\alpha,  \beta}$$ という解の式を導きだすことができたのです。しかし３次方程式だと、３つの解の差積
　$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
を考えるだけではまだ遇置換で対称性を保ち、式を変化させない対称性を保つ置換を恒等置換にまで絞り込めていません。それゆえに $${X_3}$$ を考えるだけでは、恒等置換でのみ対称性を保つ $${\alpha,  \beta,  \gamma}$$ という式は作れないことになります。
　よって３次方程式の場合、対称性を保つ置換を、遇置換からさらに恒等置換にまで絞り込む必要があり、それを解説するのが今日のゼミの目的です」
　竹村先生の家庭教師が、森田君の中では本格的に”ゼミ”になっている。森田君は続ける。
「まずは３次方程式の解と係数の関係を確認しておきます。

＜３次方程式の解と係数の関係（復習）＞
　３次方程式 $${ax^3+bx^2+cx+d=0}$$ の $${3}$$ つの解を $${\alpha, \beta}$$, $${\gamma}$$ とすると、次の等式が成り立つ。

$$
\begin{align*}
\alpha+\beta+\gamma&=-\dfrac{b}{a}\\
\alpha\beta+\beta\gamma+\gamma\alpha&=\dfrac{c}{a}\\
\alpha\beta\gamma&=-\dfrac{d}{a}
\end{align*}
$$

これを、チルンハウス変換を施した $${y}$$ についての３次方程式 $${y^3+py+q=0}$$ に適用すると
　$${a=1,  b=0,  c=p,  d=q}$$
となるので

$$
\begin{align*}
\alpha+\beta+\gamma&=-\dfrac{0}{1}\\
\alpha\beta+\beta\gamma+\gamma\alpha&=\dfrac{p}{1}\\
\alpha\beta\gamma&=-\dfrac{q}{1}
\end{align*}
$$

より

$$
\begin{align*}
\alpha+\beta+\gamma&=0\\
\alpha\beta+\beta\gamma+\gamma\alpha&=p\\
\alpha\beta\gamma&=-q
\end{align*}
$$

よって

$$
\begin{align*}
p&=\alpha\beta+\beta\gamma+\gamma\alpha\\
q&=-\alpha\beta\gamma
\end{align*}
$$

　すると、ここで注目したいのは、３次方程式 $${y^3+py+q=0}$$ の係数 $${p}$$ と $${q}$$ は、３変数の基本対称式で表せるということです。

$$
\begin{align*}
p&=\underbrace{\alpha\beta+\beta\gamma+\gamma\alpha}_{基本対称式}\\
q&=-\hspace{-7pt}\underbrace{\alpha\beta\gamma}_{基本対称式}
\end{align*}
\hspace{5pt}\cdots (*1)
$$

３変数の基本対称式は
　$${\alpha+\beta+\gamma}$$
　$${\alpha\beta+\beta\gamma+\gamma\alpha}$$
　$${\alpha\beta\gamma}$$
ですが、$${p,  q}$$ を $${(*1)}$$ のように基本対称式で表すことができました。
　これは、先ほどの２次方程式 $${x^2+a_1x+a_2=0}$$ について

$$
\begin{align*}
a_1&=-(\hspace{-5pt}\underbrace{\alpha+\beta}_{基本対称式}\hspace{-5pt})\\
a_2&=\underbrace{\alpha\beta}_{基本対称式}
\end{align*}
$$

と、基本対称式で表せたことと同様です。２次方程式の係数 $${a_1,  a_2}$$ がダイレクトに基本対称式で表せたように、３次方程式の係数 $${p,  q}$$ もダイレクトに基本対称式で表せるわけです。
　すると、$${y^3+py+q=0}$$ の係数 $${p,  q}$$ は基本対称式そのものなので、$${p,  q}$$ の加減乗除で表される式は必ず対称式となります。例えば下記のような式は $${\alpha,  \beta,  \gamma}$$ をどのように入れ替えても、つまりすべての３次置換を作用させてもその式は変わらないので対称式です。

$$
\begin{align*}
2p+q&=2(\alpha\beta+\beta\gamma+\gamma\alpha)+\alpha\beta\gamma & &\rightarrow 対称式\\
3p\cdot q&=3(\alpha\beta+\beta\gamma+\gamma\alpha)\alpha\beta\gamma & &\rightarrow 対称式\\
\dfrac{{p}^2+4}{5q}
&=\dfrac{(\alpha\beta+\beta\gamma+\gamma\alpha)^2+4}{5\alpha\beta\gamma} & &\rightarrow 対称式
\end{align*}
$$

２次方程式のときと同じように、$${2}$$ や $${4}$$ のような、我々が知っている普通に使っている数は加減乗除に用いてもかまいません。対称性は基本対称式 $${\alpha\beta+\beta\gamma+\gamma\alpha}$$ と$${\alpha\beta\gamma}$$ の部分に依存し、その部分は $${\alpha,  \beta,  \gamma}$$ をどのように入れ替えても式は変わりません。よって $${\alpha\beta+\beta\gamma+\gamma\alpha}$$ と$${\alpha\beta\gamma}$$ を基本パーツとして式を構成しても、その式の対称性は保たれるからです。逆に

$$
\begin{align*}
\boldsymbol{\small 対称式は基本対称式の加減乗除で表すことができる}
\end{align*}
$$

という『対称式の基本定理』より、すべての対称式は３変数の基本対称式
　$${\alpha+\beta+\gamma}$$
　$${\alpha\beta+\beta\gamma+\gamma\alpha}$$
　$${\alpha\beta\gamma}$$
の加減乗除で表すことができます。すると１番上は $${\alpha+\beta+\gamma=0}$$ となることも含め、３変数の解と係数の関係 $${(*1)}$$

$$
\begin{align*}
\alpha\beta+\beta\gamma+\gamma\alpha&=p\\
\alpha\beta\gamma&=-q
\end{align*}
\hspace{5pt}\cdots (*1)
$$

より、すべての対称式は $${p,  q}$$ の加減乗除で表すことができます。つまり $${p,  q}$$ の加減乗除で表せる式の集合と、対称式の集合は等しくなるわけです」と、森田君はホワイトボードに図を書き始めた。

「これはさっきやった２次方程式 $${x^2+a_1x+a_2=0}$$ のときと同じ考え方だね」と竹村は補足を入れた。（$${\Rightarrow}$$ 詳しくは本シリーズ (11) ）

「はい、同じ考え方です。２次方程式の解 $${\alpha,  \beta}$$ を係数 $${a_1,  a_2}$$ で表すことができれば解の公式は完成しますが、解の式 $${\alpha,  \beta}$$ は対称式ではないので、基本対称式である係数 $${a_1,  a_2}$$ の加減乗除では表すことができませんでした。それは３次方程式でも同じことが言えて、３次方程式の解を表す式 $${\alpha,  \beta,  \gamma}$$ は対称式ではないので、基本対称式である係数 $${p,  q}$$ の加減乗除で表すことは出来ないわけです」
「そこでアイデアが必要ということだね」
「そうです。そのアイデアについて、自分の考えたことを話していこうと思います。さて前の授業で、差積の２乗
　$${(X_3)^2=\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}$$
は、次のように表せることを証明しました。（$${\Rightarrow}$$ 証明は本シリーズ (9)）

$$
\begin{align*}
\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2=-4\cdot27\left\{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3\right\}
\end{align*}
  \cdots (*2)
$$

３次方程式 $${y^3+py+q=0}$$ の解 $${\alpha,  \beta,  \gamma}$$ の差積の２乗は、その３次方程式の係数 $${p,  q}$$ で表される、という等式です。またこれは、３次方程式 $${ax^3+bx^2+cx+d=0}$$ の解の公式

$$
{\begin{align*}
x= \begin{cases}
-\dfrac{b}{3a}+\sqrt[3]{
-\dfrac{q}{2}+\sqrt{
\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}
}}
+\sqrt[3]{
-\dfrac{q}{2}-\sqrt{
\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}
}}\\
-\dfrac{b}{3 a}+\omega\sqrt[3]{
-\dfrac{q}{2}+\sqrt{
\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}
}}
+\omega^2\sqrt[3]{
-\dfrac{q}{2}-\sqrt{
\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}
}}\\
-\dfrac{b}{3a}+\omega^2\sqrt[3]{
-\dfrac{q}{2}+\sqrt{
 \left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}
}}
+\omega\sqrt[3]{
-\dfrac{q}{2}-\sqrt{
\left(\dfrac{q}{2}\right)^{2}+\left(\dfrac{p}{3}\right)^{3}
}}
\end{cases}
\end{align*}}
$$

ただし

$$
{\begin{align*}
p&=-\frac{1}{3}\left(\frac{b}{a}\right)^{2}+\frac{c}{a}\\
q&=\frac{2}{27}\left(\frac{b}{a}\right)^{3}-\frac{1}{3}\left(\frac{b}{a}\right)\left(\frac{c}{a}\right)+\frac{d}{a}
\end{align*}}
$$

について、その平方根 $${\sqrt{\hspace{15pt}}}$$ の中身 $${\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}$$ が、差積の２乗
　$${(X_3)^2=\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}$$
で表されることも意味しています。具体的には $${(*2)}$$ 式の両辺を $${-4\cdot27}$$ で割れば

$$
\begin{align*}
\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3=\dfrac{1}{-4\cdot27}\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2
\end{align*}
$$

となります。（$${\Rightarrow}$$ 詳しくは本シリーズ (9)）
　これから述べていきますが、差積は解の公式の導出と密接した関連があるわけです。
　ここで復習ですが、①～③の遇置換では $${(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$ は変化しませんでした。

$$
\begin{rcases}
➀\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}\\
\\
②\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}\\
\\
③\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
\end{rcases}
\hspace{8pt}では\hspace{8pt}
\begin{align*}
&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\longrightarrow (\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)
\end{align*}
$$

一方④～➅の奇置換では、$${(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$ は $${-1}$$ 倍と変化しました。

$$
\begin{rcases}
④\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}\\
\\
➄\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}\\
\\
➅\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
\end{rcases}
\hspace{8pt}では\hspace{8pt}
\begin{align*}
&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\longrightarrow -(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)
\end{align*}
$$

つまり差積
　$${(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
に奇置換を作用させるとプラスとマイナスが入れ替わります。ここで先ほど紹介した $${(*2)}$$ 式をご覧ください。

$$
\begin{align*}
\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2=-4\cdot27\left\{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3\right\}
\end{align*}
  \cdots (*2)
$$

簡単のため、左辺を $${Z}$$ とおきます。

$$
\begin{align*}
\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2=Z
\end{align*}
$$

ここで両辺の平方根をとると

$$
\begin{align*}
(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)=\pm\sqrt{Z}
\end{align*}
$$

$${Z=-4\cdot27\left\{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3\right\}}$$ だったので

$$
\begin{align*}
(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)=\pm\sqrt{-4\cdot27\left\{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3\right\}}
\end{align*}
  \cdots (*3)
$$

平方根を取ると、平方根 $${\sqrt{\hspace{15pt}}}$$ の前にプラスマイナス $${\pm}$$ が現れます。平方根を取ることによって必然的にプラスマイナスの不定性、プラスかマイナスかの定まらない性質が現れます。
　さてこの式 $${(*3)}$$ 式をみると、左辺 $${(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$ の奇置換によるプラスマイナスの変換性は、平方根  $${\sqrt{\hspace{15pt}}}$$ の部分

$$
\begin{align*}
\sqrt{-4\cdot27\left\{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3\right\}}
\end{align*}
$$

のプラスマイナスの変換に対応していることがわかります。例えばプラスの方を $${(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$ として採用すると

$$
\begin{align*}
(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)=+\sqrt{-4\cdot27\left\{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3\right\}}
\end{align*}
$$

この両辺に奇置換を作用させると、左辺は $${-1}$$ 倍と変化、右辺の平方根 $${\sqrt{\hspace{15pt}}}$$ の中身は対称式で変化しないので

$$
\begin{align*}
-(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)=+\sqrt{-4\cdot27\left\{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3\right\}}\\
\end{align*}
$$

両辺に $${-1}$$ を掛けて

$$
\begin{align*}
(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)=-\sqrt{-4\cdot27\left\{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3\right\}}\\
\end{align*}
$$

と平方根にマイナスが付きます。さらに両辺にもう一度奇置換を作用させると、再び左辺は $${-1}$$ 倍、右辺はそのままで

$$
\begin{align*}
-(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)=-\sqrt{-4\cdot27\left\{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3\right\}}\\
\end{align*}
$$

両辺に $${-1}$$ を掛けて

$$
\begin{align*}
(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)=+\sqrt{-4\cdot27\left\{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3\right\}}\\
\end{align*}
$$

と、今度は平方根の符号がプラスになり、奇置換によって $${+\sqrt{\hspace{15pt}}}$$ と $${-\sqrt{\hspace{15pt}}}$$ で入れ替わります。

$$
\begin{align*}
(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)=&+\sqrt{-4\cdot27\left\{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3\right\}}\\
&\hspace{1pt}\updownarrow \boldsymbol{\small 奇置換によりプラスマイナスが入れ替わる}\\
(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)=&-\sqrt{-4\cdot27\left\{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3\right\}}
\end{align*}
$$

ここから抽象的な解説に入っていきますが、ここで以前計算したラグランジュ・リゾルベント

$$
\begin{align*}
A=\alpha+\omega\beta+\omega^2\gamma\\
B=\alpha+\omega^2\beta+\omega\gamma
\end{align*}
$$

の３乗

$$
\begin{align*}
A^3&=27\left\{-\dfrac{q}{2}+\underline{\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}\right\}\\
B^3&=27\left\{-\dfrac{q}{2}-\underline{\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}\right\}
\end{align*}
$$

を観察してみます。（$${\Rightarrow}$$ 証明は本シリーズ (7)）
　ラグランジュ・リゾルベントの３乗 $${A^3,  B^3}$$ の中に、$${\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}$$ の平方根 $${\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}$$ が下線部に現れます。先ほど求めた $${(*3)}$$ 式

$$
\begin{align*}
(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)=\pm\sqrt{-4\cdot27\underline{\left\{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3\right\}}}
\end{align*}
  \cdots (*3)
$$

にも $${-4\cdot27}$$ が付いていますが $${\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}$$ の平方根 $${\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}$$ が下線部に現れます。
　$${-4\cdot27}$$ が掛けてあるかないかの違いはありますが、$${-4\cdot27}$$ の部分は我々が知っている普通の数の加減乗除なので本質的ではありません（注１）。$${\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}$$ を含む平方根 $${\sqrt{\hspace{15pt}}}$$ の部分の、プラスとマイナスが入れ替わる、その構造そのものが重要です。
　この構造によって、ラグランジュ・リゾルベントの３乗 $${A^3}$$ と $${B^3}$$ の入れ替えと、平方根 $${\sqrt{\hspace{15pt}}}$$ の前のプラスとマイナスの入れ替えを１対１に対応させることを可能にしています。

$$
\begin{align*}
A^3&=27\left\{-\dfrac{q}{2}+\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}\right\}\\
\boldsymbol{\small A^3  と  B^3  の入れ替え}\hspace{1pt}\updownarrow\hspace{5pt}&\hspace{50pt}\updownarrow\boldsymbol{\small \pm  の入れ替え}\\
B^3&=27\left\{-\dfrac{q}{2}-\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}\right\}
\end{align*}
$$

これは２次方程式の解の公式で、$${\alpha}$$ と $${\beta}$$ の解の入れ替えと、平方根の前のプラスとマイナスの入れ替えが１対１で対応していることと同じ構造です。

$$
\begin{align*}
&\alpha=\dfrac{-b+\sqrt{b^2-4bc}}{2a}\\
\boldsymbol{\small 解の入れ替え}\hspace{2pt}&\hspace{-1pt}\updownarrow\hspace{30pt}\updownarrow\boldsymbol{\small \pm  の入れ替え}\\
&\beta=\dfrac{-b-\sqrt{b^2-4bc}}{2a}
\end{align*}
$$

同じ構造が現れる理由は、３次方程式の解の公式を導くにあたって最初に２次方程式の解の公式を用いているからです。つまり２次方程式では
　$${X_2=\alpha-\beta}$$
３次方程式では
　$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\beta)}$$
という「差積」という共通項を通じて、２次方程式ではその解 $${\alpha,  \beta}$$ の入れ替えを、３次方程式では $${A^3}$$ と $${B^3}$$ の入れ替えを、「差積の２乗の平方根を取る」ことによって必然的に生じるプラスマイナスの入れ替えへと対応させているわけです。

　さて、次に説明するのは『添加』です。２次方程式では、係数で表される式の集合に、係数の加減乗除では表せない平方根を添加しましたが、３次方程式でも平方根を添加します。ラグランジュ・リゾルベントの３乗

$$
\begin{align*}
A^3&=27\left\{-\dfrac{q}{2}+\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}\right\}\\
B^3&=27\left\{-\dfrac{q}{2}-\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}\right\}
\end{align*}
$$

を求めるためには、その式の中にある
　$${\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}$$
を求める必要があります。しかしそれは、$${y^3+py+q=0}$$ の係数 $${p,  q}$$ の加減乗除で表すことはできません。もちろん加減乗除に $${2}$$ や $${3}$$ のような普通に用いている数を用いてもかまいません。
　$${\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}$$
を、$${p,  q}$$ と普通の数の加減乗除で表すことはできないわけです。そこで、 $${p,  q}$$ で表される式の集合に、条件Ⅰの「解の式 $${X}$$」を満たす差積 $${X_3}$$ について、それを２乗 して平方根を取った $${\sqrt{(X_3)^2}}$$

$$
\begin{align*}
\sqrt{(X_3)^2}=\sqrt{\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}
\end{align*}
$$

を添加します。この式を添加することによって、$${(*2)}$$ 式 

$$
\begin{align*}
\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2=-4\cdot27\left\{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3\right\}
\end{align*}
  \cdots (*2)
$$

の両辺を、平方根でそのまま被せた次の等式

$$
\begin{align*}
\sqrt{\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}=\sqrt{-4\cdot27\left\{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3\right\}}
\end{align*}
$$

により、$${-4\cdot27}$$ という係数が掛けられてはいますが、この等式の左辺、つまり差積の２乗の平方根
　$${\sqrt{(X_3)^2}=\sqrt{\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}}$$
の値が存在していれば、この等式の右辺の値も存在、ひいてはその右辺の平方根の中身の値も存在し、結果 $${\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}$$ の値も存在するので
　$${\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}$$
の値も存在しています（注２）。すなわち
　$${\sqrt{(X_3)^2}=\sqrt{\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}}$$
を添加することと
　$${\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}$$
を添加することは同じことになります。つまり、この差積の２乗の平方根
　$${\sqrt{(X_3)^2}=\sqrt{\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}}$$
の添加された式の集合、つまり拡大された数体系の中では、ラグランジュ・リゾルベントの３乗 $${A^3,  B^3}$$ を、係数 $${p,  q}$$ と平方根 $${\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}$$ の加減乗除で表すことが可能となるわけです」
　と言いながら森田君は大きく図を書き始めている。巨大な壁のホワイトボードが役立っている。

「平方根を使えるようになったことがポイントです。なお下図のように $${\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}$$ を添加しても問題ありません。上で説明したように
　$${\sqrt{(X_3)^2}=\sqrt{\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}}$$
を添加することと
　$${\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}$$
を添加することは同じことになるからです（注２）。加減乗除の計算で解の公式が得られるものであれば、添加する式に自由度があります」

「これでラグランジュリゾルベントの３乗 $${A^3,  B^3}$$ を、次のように $${p,  q}$$ と  $${\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}$$ で表せたと同時に、$${A^3,  B^3}$$ の両者をプラスマイナスの対応で仕分けして導き出すことができました」

$$
\begin{align*}
A^3&=27\left\{-\dfrac{q}{2}+\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}\right\}\\
B^3&=27\left\{-\dfrac{q}{2}-\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}\right\}
\end{align*}
$$

「ところで森田君」竹村はゼミらしく確認してみることにした。
「先ほど係数 $${p,  q}$$ の加減乗除で表される式の集合に、解の差積の２乗の平方根
　$${\sqrt{(X_3)^2}=\sqrt{\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}}$$
を添加すると言ったけど、差積そのもの
　$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
を添加するのとではどう違うかな？」
「同じです」森田君はきっぱりと答えた。
「$${\sqrt{(X_3)^2}}$$ は

$$
\begin{align*}
\sqrt{(X_3)^2}&=\sqrt{\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}\\
&=\pm(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&=\pm X_3
\end{align*}
$$

つまり

$$
\begin{align*}
\sqrt{(X_3)^2}=
\begin{cases}
X_3 & \\
-X_3 &
\end{cases}
\end{align*}
$$

と、$${X_3}$$ と $${-X_3}$$ のプラスとマイナス２つの値が含まれます。すると $${\sqrt{(X_3)^2}}$$ を添加すると自動的に $${X_3}$$ は添加され、逆に $${X_3}$$ を添加すると、その $${X_3}$$ に我々が普通に使っている数 $${-1}$$ を掛けると $${-X_3}$$ は得られるので、$${X_3}$$ の添加によって $${-X_3}$$ も構成できます。
　$${\sqrt{(X_3)^2}}$$ の添加 $${\longrightarrow}$$$${X_3}$$ の添加
　$${X_3}$$ の添加 $${\longrightarrow}$$$${-X_3}$$ は構成可能 $${\longrightarrow}$$ $${\sqrt{(X_3)^2}}$$ の添加
すなわち
　『$${\sqrt{(X_3)^2}}$$ を添加するのと $${X_3}$$ を添加するのは同じ』
こととなり、添加したおのおのの集合の範囲も同じ範囲となります。

以上のように、添加する式は１つではなく自由度があります。要は解の公式の導出に必要な平方根、ここでは
　$${\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}$$
が、加減乗除の計算対象に加わればいいのです」
「なるほど」とその説明に竹村はうなずいた。森田君は続ける。
「２次方程式ではここで終わりでしたが、３次方程式の解の公式ではここからまだ続きがあります。
　$${(X_3)^2=\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}$$
は対称式、つまり３次置換で式を変化させず対称性を保っています。しかし
　$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
は奇置換で式を変化させる、つまり３次置換で対称性はこわれていますが、遇置換では式を変化させず、まだ対称性が保たれています。

$$
\begin{rcases}
➀\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}\\
\\
②\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}\\
\\
③\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
\end{rcases}
\hspace{8pt}では\hspace{8pt}
\begin{align*}
&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\longrightarrow (\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{7pt}\Rightarrow \boldsymbol{\small 変化しない（対称性は保たれている）}\hspace{5pt}
\end{align*}
$$

$$
\begin{rcases}
④\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}\\
\\
➄\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}\\
\\
➅\hspace{5pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
\end{rcases}
\hspace{8pt}では\hspace{8pt}
\begin{align*}
&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\longrightarrow -(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
&\hspace{7pt}\Rightarrow \boldsymbol{\small -1  倍と変化（対称性はこわれている）}
\end{align*}
$$

先ほどの解説の繰り返しになりますが、２次方程式では、差積の２乗
　$${(X_2)^2={(\alpha-\beta)}^2}$$
は対称式、つまり２次置換で対称性を保っているが、差積そのもの
　$${X_2=\alpha-\beta}$$
を変化させないで対称性を保つ置換は恒等置換のみでした。それによって
　$${X_2=\alpha-\beta}$$
と同等の対称性をもつ、恒等置換でのみ対称性を保つ $${\alpha,  \beta}$$ という解の式を導きだすことができたのです。しかし３次方程式だと、３つの解の差積
　$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
を考えるだけではまだ遇置換で対称性を保ち、式を変化させない対称性を保つ置換を、恒等置換にまで絞り込めていません。それゆえに、$${X_3}$$ を考えるだけでは恒等置換でのみ対称性を保つ $${\alpha,  \beta,  \gamma}$$ という式は作れないことになります。
　よって３次方程式の場合、対称性を保つ置換を、遇置換からさらに恒等置換にまで絞り込む必要があるのです。そしてそれが次のステップです。それはラグランジュ・リゾルベントの３乗

$$
\begin{align*}
A^3&=27\left\{-\dfrac{q}{2}+\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}\right\}\\
B^3&=27\left\{-\dfrac{q}{2}-\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}\right\}
\end{align*}
$$

の３乗根を取って、ラグランジュ・リゾルベント $${A,  B}$$ そのものを求めるステップに対応していきます」
　「なるほど」と竹村はうなずいた。「ラグランジュ・リゾルベントそのものを求めることが、恒等置換まで絞り込むことにつながっていく。森田君、少し休憩をいれようか」
「分かりました」と森田君はお手洗いに向かった。
　家庭教師の終わる時間はとっくに過ぎ、西日が壁のホワイトボードをオレンジに照らしている。補足や確認を入れたいところが所々にあったが、森田君のいける所までいこうと、竹村は黙って”ゼミ”を見守ることにした。

（了）

（注１）
　この $${-4\cdot27}$$ の部分についてうまく説明し切れていない感じもあるので、今後の宿題にしておきます。本質的には平方根をとることによって必然的に生じるプラスマイナスの不定性（決まらない性質）を逆利用して、$${A^3,  B^3}$$ をプラスとマイナスに分けて求めた（どちらがプラスでどちらがマイナスか決まらない不定性を利用している）、その構造にあるのかなと考えています。
（注２）
　この解説はかなり強引のように思います（もしかして間違っている？）。「存在している」みたいなあやしい言葉でやや誤魔化しています。「差積の２乗の平方根」の添加が「ラグランジュ・リゾルベントの３乗の決定」につながっていることを簡単かつ具体的に解説したかったですが、これも今後の宿題です。ピタッとする解説があればご教授下さい。

（コメント）
　本シリーズは、３次方程式の場合と同じアイデアを５次方程式でやろうとすると矛盾が起き、よって５次以上の方程式に解の公式が存在しない、という流れになります。これは「アーベルの証明」（アーベル・ルフィニの定理）で、それを解説してから「群」という新しい概念を用いてより核心に迫った「ガロアの証明」へと続きます。
　ただ今後は図やグラフを多用したいので、図形やグラフが描けるようnote運営部にリクエストしてみようかと思います（図やグラフを描けないと他で作って画像として貼り付けることになるので、かなり面倒です）。座標に任意の数式のグラフが描けるようになればと思います。
　なるべく当時の素朴な知識だけで、現代数学の専門的なことは使わないで書いていきます。とはいえアーベルやガロアの原論文そのものだと、（当時の数学的な道具立てが未整理だったか？）日本語訳をみても非常に分かりにくいので、その急所のアイデアを忠実に守りながらも、高校数学だけで分かるように柔らかく書いていきます。

（参考）
　各テーマの内容
（１）「２次方程式の解の公式」を式変形で導出
　　　・平方完成
（２）「３次方程式の解の公式」を導出するための準備
　　　・$${1}$$ の３乗根 $${\omega}$$
（３）「３次方程式の解の公式」を式変形で導出
　　　・チルンハウス変換
（４）「解と係数の関係」と「対称式」の解説
（５）「対称式」を用いた「２次方程式の解の公式」の導出
（６）「解の置換」と「ラグランジュ・リゾルベント」の解説
（７）「ラグランジュ・リゾルベント」による「３次方程式の解の公式」の導出
（８）「遇置換」と「奇置換」の解説（ここから「アーベルの証明」の準備）
（９）「差積の２乗」が対称式となることを解説
（10）「平方根」「３乗根」と次々と累乗根を加えていくアイデア
（11）「アーベルの証明」のアイデアを用いて、なぜ「２次方程式の解の公式が存在するのか」を解説（添加する式について加筆予定）
（12）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（前編）。「差積の２乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む。
（13）（予定）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（後編）。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む。$${\longrightarrow}$$ ３次方程式の解の公式の完成