
(まとめを追記)5次方程式に解の公式が存在しないことを「可解群」で証明する
(追記)
内容はそのまままで、誤字脱字、文章を修正中です。
1 「(まとめ)証明の急所はどこか?」を追記しました。
2 3次方程式についてのガロア対応を修正
3 巡回群の説明を追記
4 定理2の証明を加筆修正
5 その他、細かい所の文章を加筆修正
(初めに)
まだ修正・推敲中ですが、応募締め切り目前なのでアップします。専門用語をなるべく控えながら厳密、かつ分かりやすく話を持っていくのが難しく、ぎりぎりまで考察中です。
なお、応募期間を過ぎても、多少の修正は可能なようです。
Q. 応募期間を過ぎたが、記事を修正しても審査対象になりますか?
A. 審査は締切時に公開された内容で行います。
受賞となった際、修正された内容が審査時の内容と著しく異なる場合は、受賞取り消しとなる場合があります。
誤字脱字や(内容を変えない)少しの文章の手直しなど、審査に影響しない範囲で修正を加えるかもしれません。まったく違う内容のものは、新しい章にして審査外で書いていきます。
***
(本文始め)
本章で、いよいよ本丸に入ります。証明すべきことは
「5次対称群は可解群ではない」
ということです。可解群ではないことをもって
「5次方程式には解の公式が存在しないこと」
が証明されます(本シリーズ (36))。
証明の前に、重要事項を整理していきます。証明のための道具立てです。
まずは群の定義です(本シリーズ (28))。
群の定義(復習)
空でない集合 $${G}$$ の任意の要素 $${a, b, c}$$ の間に1つの演算 $${*}$$ が規定されているとする。
この集合 $${G}$$ の任意の要素 $${a, b, c}$$ が、その演算 $${*}$$ に関して次の条件を満たすとき、$${G}$$ は演算 $${*}$$ に関して群であるという。
(1) $${a*b}$$ は $${G}$$ の要素である。
(2) 交換法則 $${(a*b)*c=a*(b*c)}$$ が成り立つ。
(3) $${a*e=e*a=a}$$ となる単位元 $${e}$$ が $${G}$$ に存在する。
(4) $${a*x=x*a=e}$$ となる逆元 $${x}$$ が $${G}$$ に存在する。
***
(1) を満たすことを、集合 $${\bm G}$$ は演算 $${\bm *}$$ について閉じているといいます。演算の結果、集合 $${G}$$ からはみ出さないことを意味します。
(2) は、カッコを気にしないで、どこから演算を施してもよいことを保証します。
(3) は、左右どちらから演算を施しても変化しない要素の存在です。この要素を単位元といいます。
(4) は、左右両方から演算を施すと単位元になる要素の存在です。この要素を逆元といいます。
単なる集合(要素の集まり)ではなく、集合の要素に、上記の演算規則 (1)~(4) が規定された集合が群です。
要するに群とは、イメージとして
(1) 全部そろっている
(2) どこからでもつなげることができる
(3) 変えないことができる
(4) 元に戻すことができる
の4つの条件が成り立つ要素の集まり(集合)です。
逆元について新しい表記法
ここで新しい記号を導入します。
群 $${G}$$ の要素 $${g}$$ の逆元を $${g^{-1}}$$ と表記します。読み方は”ジーインバース”です。つまり、群 $${G}$$ の演算 $${*}$$ に関して
$$
\begin{align*}
g*g^{-1}=g^{-1}*g=e{\small(単位元)}
\end{align*}
$$
を満たします。
例えば、整数の集合 $${\mathbb{Z}}$$ はたし算 $${+}$$ に関して群になりますが(本シリーズ (28))、その要素として $${g=3}$$ をとると
$$
\begin{align*}
3+(-3)=(-3)+3=0{\small(単位元)}
\end{align*}
$$
より、$${g=3}$$ の逆元は $${g^{-1}=-3}$$ となります。
3次対称群の要素における逆元
他にも例を上げます。3次対称群
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
について、それぞれの要素は次の置換です。
$$
\begin{align*}
&\begin{rcases}
id=
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=I\\
\\
\rho_2=
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha \gamma \beta)\\
\\
\rho_3=
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=(\alpha \beta \gamma)
\end{rcases}遇置換\\
\\
&\begin{rcases}
\tau_1=
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
\tau_2=
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}\\
\\
\tau_3=
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}奇置換
\end{align*}
$$
遇置換とは偶数個の互換の合成(これを積という)で表せる置換であり、奇置換とは奇数個の互換の積で表せる置換です(本シリーズ (15))。
この $${S_3}$$ の群表(積の対応表)は、次のようになります(本シリーズ (28))。
$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c|c|c|c}
& id & \underline{\rho_2} & \underline{\rho_3} & \tau_1 & \tau_2 & \utilde{\tau_3}\\ \hline\hline
id & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3\\ \hline
\underline{\rho_2} & \rho_2 & \rho_3 & \underline{id} & \tau_3 & \tau_1 & \tau_2\\ \hline
\underline{\rho_3} & \rho_3 & \underline{id} & \rho_2 & \tau_2 & \tau_3 & \tau_1\\ \hline
\tau_1 & \tau_1 & \tau_2 & \underline{\tau_3} & id & \rho_2 & \rho_3\\ \hline
\tau_2 & \tau_2 & \tau_3 & \tau_1 & \rho_3 & id & \rho_2\\ \hline
\utilde{\tau_3} & \tau_3 & \tau_1 & \tau_2 & \rho_2 & \rho_3 & \utilde{id}
\end{array}
$$
この対応表から
(例1)
$${\rho_2\rho_3=\rho_3\rho_2=id}$$(下線部)より
$${\rho_2}$$ の逆元は $${\rho_2^{-1}=\rho_3}$$
$${\rho_3}$$ の逆元は $${\rho_3^{-1}=\rho_2}$$
逆元は上式の下線部をみれば分かります。作用させて恒等置換 $${id}$$ になるもの同士が、互いに逆元になります。
(例2)
$${\tau_3\tau_3=id}$$(波線部)より
$${\tau_3}$$ の逆元は $${\tau_3}$$
上式の波線部より、作用させて恒等置換 $${id}$$ になるもの同士が互いに逆元です。
なお、互換は逆元をとっても変化しません。$${\beta}$$ と $${\gamma}$$ を入れ変えた後、もう一度 $${\beta}$$ と $${\gamma}$$ を入れ換えると元に戻るので
$${\tau_3\tau_3=id}$$(波線部)
つまり
$${(\beta \gamma)(\beta \gamma)=id}$$
より
$${{(\beta \gamma)}^{-1}=(\beta \gamma)}$$
となります。一般に、任意の互換の逆元は同じものになります。
部分群の定義(復習)
ある群 $${G}$$ の空でない部分集合 $${H}$$ が同じ演算で群になるとき、その部分集合 $${H}$$ を、 $${G}$$ の部分群といいます(本シリーズ (29))。
ここで重要なのは、あくまでも”同じ演算で”ということです。もとの群がたし算に関して群になる場合、その部分群もたし算に関して群になります。

(例)
3次対称群
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
の部分群は
$${\{id\}}$$
$${\{id, \tau_1\}}$$
$${\{id, \tau_2\}}$$
$${\{id, \tau_3\}}$$
$${\{id, \rho_2, \rho_3\}}$$
$${S_3}$$
正規部分群の定義(復習)
$${N}$$ を群 $${G}$$ の部分群とする。$${G}$$ のすべての要素 $${g}$$ について
$$
\begin{align*}
gN=Ng
\end{align*}
$$
を満たすとき、$${N}$$ を $${G}$$ の正規部分群という。
***
方程式に解の公式が存在するかどうかを議論するには、ただの部分群ではなく正規部分群であることが重要です。それは
正規部分群による剰余類の類別は、左剰余類と右剰余類とで等しくなる(本シリーズ (30))
正規部分群による剰余類の集合は群(剰余群)になる(本シリーズ (31))
など、重要な性質があるからです。
正規部分群の発見は、ガロアによる偉大な業績のひとつです。
(例)
3次対称群
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
の部分群
$${\{id\}}$$
$${\{id, \tau_1\}}$$
$${\{id, \tau_2\}}$$
$${\{id, \tau_3\}}$$
$${\{id, \rho_2, \rho_3\}}$$
$${S_3}$$
のうち、正規部分群は
$${\{id\}}$$
$${\{id, \rho_2, \rho_3\}}$$
$${S_3}$$
剰余群について新しい表記法
ここで、剰余群について新しい表記法を導入します。
群 $${G}$$ の正規部分群 $${N}$$ を考えたとき、$${G}$$ の $${N}$$ による剰余類の集合を $${G/N}$$ と表記します。この集合は
$${aN\circ bN=abN}$$
という演算に関して群になります。この群のことを、$${G}$$ の $${N}$$ による剰余群といいます。なお $${a, b}$$ は $${G}$$ の任意の要素です(本シリーズ (31))。
解の公式が存在するかどうかは、この剰余群が巡回群になることが鍵を握ります(本シリーズ (33))。
この表記に関して、2次方程式についてのガロア対応(本シリーズ (36))
$$
\begin{align*}
&\hspace{-10pt}{\footnotesize X_2 を添加}\\[-3pt]
&\hspace{4pt}\downarrow\\
{\small \bm{<体の拡大>}}\hspace{8pt}Q_2&\hspace{-1pt}\overset{\bm{拡大}}{\subset} Q_2(X_2)\\
\Updownarrow{\scriptsize \bm{対応}}\hspace{-15pt}&\hspace{25pt}\Updownarrow {\scriptsize \bm{対応}}\\
{\small \bm{<群の縮小>}}\hspace{8pt}S_2\hspace{0pt}&\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_2 の正規部分群}{I}\\[-4pt]
&\hspace{4pt}\uparrow\\[-2pt]
&\hspace{-10pt}{\footnotesize \{idI, \tau I\} \atop が巡回群}
\end{align*}
$$
をみると
$${S_2=\{id, \tau\}}$$
の正規部分群 $${I=\{id\}}$$ による剰余群は
$$
\begin{align*}
S_2/I=\{idI, \tau I\}
\end{align*}
$$
と表記されます。この表記に変えると、先ほどの2次方程式についてのガロア対応は
$$
\begin{align*}
&\hspace{-10pt}{\footnotesize X_2 を添加}\\[-3pt]
&\hspace{4pt}\downarrow\\
{\small \bm{<体の拡大>}}\hspace{8pt}Q_2&\hspace{-1pt}\overset{\bm{拡大}}{\subset} Q_2(X_2)\\
\Updownarrow{\scriptsize \bm{対応}}\hspace{-15pt}&\hspace{25pt}\Updownarrow {\scriptsize \bm{対応}}\\
{\small \bm{<群の縮小>}}\hspace{8pt}S_2\hspace{0pt}&\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_2 の正規部分群}{I}\\[-4pt]
&\hspace{4pt}\uparrow\\[-2pt]
&\hspace{-10pt}{\footnotesize A_2/I \atop が巡回群}
\end{align*}
$$
となります。
また、3次方程式についてのガロア対応(本シリーズ (37))
$$
\begin{align*}
&\hspace{5pt}{\footnotesize X_3 を添加}\hspace{8pt}{\footnotesize A を添加}\\[-4pt]
&\hspace{17pt}\downarrow\hspace{37pt}\downarrow\\[-2pt]
{\small \bm{<体の拡大>}}\hspace{10pt}&\hspace{-5pt}{\scriptsize Q_3(\omega)}\hspace{-2pt}\overset{\bm{拡大}}{\subset}\hspace{-5pt}{\scriptsize Q_3(\omega, X_3)}\hspace{-4pt}\overset{\bm{拡大}}{\subset}\hspace{-4pt}{\scriptsize Q_3(\omega, X_3, A)}\\
&\hspace{-1pt}\Updownarrow {\footnotesize \bm{対応}}\hspace{11pt}\Updownarrow {\footnotesize \bm{対応}}\hspace{13pt}\Updownarrow {\footnotesize \bm{対応}}\\
{\small \bm{<群の縮小>}}\hspace{10pt}&S_3\hspace{3pt}\overset{\bm{縮小}}{\supset}\hspace{-7.5pt}\underset{\tiny S_3 の正規部分群}{N}\hspace{-7.5pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny N の正規部分群}{I}\\[-4pt]
&\hspace{17pt}\uparrow\hspace{37pt}\uparrow\\[-2pt]
&\hspace{-4pt}{\footnotesize \{idN, \tau_1N\} \atop が巡回群}\hspace{2pt}{\footnotesize \{idI, \rho_2I, \rho_3I\} \atop が巡回群}
\end{align*}
$$
をみると、3次対称群
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
の正規部分群 $${N=\{id, \rho_2, \rho_3\}}$$ による剰余群は
$$
\begin{align*}
S_3/N=\{idN, \tau_1N\}
\end{align*}
$$
と表記されます。さらに
$${N=\{id, \rho_2, \rho_3\}}$$
の正規部分群 $${I=\{id\}}$$ による剰余群は
$$
\begin{align*}
N/I=\{id I, \rho_2I, \rho_3I\}
\end{align*}
$$
と表記されます。この表記に変えると、先ほどの3次方程式のガロア対応は
$$
\begin{align*}
&\hspace{5pt}{\footnotesize X_3 を添加}\hspace{8pt}{\footnotesize A を添加}\\[-4pt]
&\hspace{17pt}\downarrow\hspace{37pt}\downarrow\\[-2pt]
{\small \bm{<体の拡大>}}\hspace{10pt}&\hspace{-5pt}{\scriptsize Q_3(\omega)}\hspace{-2pt}\overset{\bm{拡大}}{\subset}\hspace{-5pt}{\scriptsize Q_3(\omega, X_3)}\hspace{-4pt}\overset{\bm{拡大}}{\subset}\hspace{-4pt}{\scriptsize Q_3(\omega, X_3, A)}\\
&\hspace{-1pt}\Updownarrow {\footnotesize \bm{対応}}\hspace{11pt}\Updownarrow {\footnotesize \bm{対応}}\hspace{13pt}\Updownarrow {\footnotesize \bm{対応}}\\
{\small \bm{<群の縮小>}}\hspace{10pt}&S_3\hspace{3pt}\overset{\bm{縮小}}{\supset}\hspace{-7.5pt}\underset{\tiny S_3 の正規部分群}{N}\hspace{-7.5pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny N の正規部分群}{I}\\[-4pt]
&\hspace{17pt}\uparrow\hspace{37pt}\uparrow\\[-2pt]
&\hspace{4pt}{\footnotesize S_3/N \atop が巡回群}\hspace{7pt}{\footnotesize N/I \atop が巡回群}
\end{align*}
$$
となります。
可換群の定義
ここで新たに可換群を定義します。
群 $${G}$$ の任意の要素 $${a, b}$$ について $${ab=ba}$$ を満たすとき、$${G}$$ は『可換群』、または『アーベル群』といいます。
***
すべての要素について、積の順番を入れ換えても同じになる群が可換群です。この法則を『交換法則』といいます。交換が可能という意味で可換群といいます。
なお、可換群と可解群は、名前が似ていますがまったく違う概念なので注意してください。
2次対称群、3次交代群は可換群であること
例えば、2次対称群 $${S_2=\{id, \tau\}}$$ は可換群です。これは下記の群表から分かります。
$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
& id & \tau\\ \hline\hline
id & id & \underline{\tau}\\ \hline
\tau & \underline{\tau} & id
\end{array}
$$
$${id\tau=\tau id (=\tau)}$$(下線部)
より交換法則が成り立つので、$${S_2}$$ は可換群となります。可換群となる群表は、右斜め下の対角線に関して線対称になります。

なお、$${S_2}$$ は $${\tau}$$ を生成元とする巡回群になり、次のように表記されます(本シリーズ (33), (34))。
$${S_2=\{id, \tau\}=\langle\tau \rangle}$$
また、3次交代群 $${A_3=\{id, \rho_2, \rho_3\}}$$ も可換群です(本シリーズのガロアの証明では $${N}$$ と表記)。これも下記の群表から分かります。
$$
\def\arraystretch{1.5}
\hspace{25pt}後\\
\raisebox{-10pt}{先}
\hspace{4pt}
\begin{array}{c||c|c|c}
& id & \rho_2 & \rho_3\\ \hline\hline
id & id & \underline{\rho_2} & \utilde{\rho_3}\\ \hline
\rho_2 & \underline{\rho_2} & \rho_3 & \underlinesegment{id} \\ \hline
\rho_3 & \utilde{\rho_3} & \underlinesegment{id} & \rho_2
\end{array}
$$
$${id\rho_2=\rho_2id (=\rho_2)}$$(下線部)
$${id\rho_3=\rho_3id (=\rho_3)}$$(破線部)
$${\rho_3\rho_2=\rho_2\rho_3 (=id)}$$($${\underlinesegment{\hspace{5pt}}}$$ 線部)
より交換法則が成り立つので、$${A_3}$$ は可換群になります。この群表も、右斜め下の対角線に関して線対称になります。

なお、$${A_3}$$ は $${\rho_2}$$ を生成元とする巡回群になり、次のように表記されます(本シリーズ (33))。
$${A_3=\{id, \rho_2, \rho_3\}=\langle\rho_2 \rangle}$$
3次対称群は可換群ではないこと
一方、3次対称群 $${S_3=\{id, \rho_2, \rho_3, \rho_1, \rho_2, \rho_3\}}$$ は可換群ではありません。下記の群表
$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c|c|c|c}
& id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3\\ \hline\hline
id & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3\\ \hline
\rho_2 & \rho_2 & \rho_3 & id & \tau_3 & \tau_1 & \tau_2\\ \hline
\rho_3 & \rho_3 & id & \rho_2 & \tau_2 & \tau_3 & \tau_1\\ \hline
\tau_1 & \tau_1 & \tau_2 & \tau_3 & id & \rho_2 & \rho_3\\ \hline
\tau_2 & \tau_2 & \tau_3 & \tau_1 & \rho_3 & id & \rho_2\\ \hline
\tau_3 & \tau_3 & \tau_1 & \tau_2 & \rho_2 & \rho_3 & id
\end{array}
$$
より
$${\tau_1\rho_3=\tau_3}$$(下線部)
$${\rho_3\tau_1=\tau_2}$$(下線部)
なので
$${\tau_1\rho_3\ne\rho_3\tau_1}$$
となり、交換法則は成り立ちません。可換群であるためには、すべての要素について交換法則が成り立たなければならないので、一つでも成り立たなければ可換群ではありません。
ガロア対応における可換群
さらに、2次方程式についてのガロア対応について
$$
\begin{align*}
&\hspace{-10pt}{\footnotesize X_2 を添加}\\[-3pt]
&\hspace{4pt}\downarrow\\
{\small \bm{<体の拡大>}}\hspace{8pt}Q_2&\hspace{-1pt}\overset{\bm{拡大}}{\subset} Q_2(X_2)\\
\Updownarrow{\scriptsize \bm{対応}}\hspace{-15pt}&\hspace{25pt}\Updownarrow {\scriptsize \bm{対応}}\\
{\small \bm{<群の縮小>}}\hspace{8pt}S_2\hspace{0pt}&\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_2 の正規部分群}{I}\\[-4pt]
&\hspace{4pt}\uparrow\\[-2pt]
&\hspace{-10pt}{\footnotesize A_2/I \atop が巡回群}
\end{align*}
$$
巡回群 $${S_2/I=\{idI, \tau I\}=\langle\tau I \rangle}$$ は可換群です。群表は、右斜め下の対角線に関して線対称になります。
$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & idN & \tau_1N\\ \hline\hline
idN & idN & \tau_1N\\ \hline
\tau_1N & \tau_1N & idN
\end{array}
$$
また、3次方程式についてガロア対応について
$$
\begin{align*}
&\hspace{5pt}{\footnotesize X_3 を添加}\hspace{8pt}{\footnotesize A を添加}\\[-4pt]
&\hspace{17pt}\downarrow\hspace{37pt}\downarrow\\[-2pt]
{\small \bm{<体の拡大>}}\hspace{10pt}&\hspace{-5pt}{\scriptsize Q_3(\omega)}\hspace{-2pt}\overset{\bm{拡大}}{\subset}\hspace{-5pt}{\scriptsize Q_3(\omega, X_3)}\hspace{-4pt}\overset{\bm{拡大}}{\subset}\hspace{-4pt}{\scriptsize Q_3(\omega, X_3, A)}\\[-3pt]
&\hspace{17pt}\Updownarrow\hspace{7pt}{\footnotesize 対応}\hspace{7pt}\Updownarrow\\[-2pt]
{\small \bm{<群の縮小>}}\hspace{10pt}&S_3\hspace{3pt}\overset{\bm{縮小}}{\supset}\hspace{-7.5pt}\underset{\tiny S_3 の正規部分群}{N}\hspace{-7.5pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny N の正規部分群}{I}\\[-4pt]
&\hspace{17pt}\uparrow\hspace{37pt}\uparrow\\[-2pt]
&\hspace{4pt}{\footnotesize S_3/N \atop が巡回群}\hspace{7pt}{\footnotesize N/I \atop が巡回群}
\end{align*}
$$
巡回群 $${S_3/N=\{idN, \tau_1N\}=\langle\tau_1N\rangle}$$ は可換群であり
$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & idN & \tau_1N\\ \hline\hline
idN & idN & \tau_1N\\ \hline
\tau_1N & \tau_1N & idN
\end{array}
$$
巡回群 $${N/I=\{idI, \rho_2I, \rho_3I\}=\langle\rho_2I\rangle}$$ も可換群です。
$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & idI & \utilde{\underline{\rho_2I}} & \rho_3I\\ \hline\hline
idI & idI & \rho_2I & \rho_3I\\ \hline
\underline{\rho_2I} & \rho_2I & \underline{\rho_3I} & idI\\ \hline
\utilde{\rho_3I} & \rho_3I & \utilde{idI} & \rho_2I
\end{array}
$$
群表はいずれも、右斜め下の対角線に関して線対称になります。
定理1 巡回群ならば可換群である
さて、可換群の例をいくつか見てきましたが、実は巡回群はすべて可換群になります。
「定理1」
巡回群ならば可換群である。
***
先に述べた例をみると、確かに巡回群
$${S_2=\{id, \tau\}=\langle\tau\rangle}$$
$${N(=A_3)=\{id, \rho_2, \rho_3\}=\langle\rho_2\rangle}$$
$${S_2/I=\{idI, \tau I\}=\langle\tau I\rangle}$$
$${S_3/N=\{idN, \tau_1 N\}=\langle\tau_1N\rangle}$$
$${N/I=\{idI, \rho_2I, \rho_3I\}=\langle\rho_2I\rangle}$$
は、すべて可解群になります。
それではこの「定理1」を証明します。
(証明)
$${G}$$ を巡回群とすると、$${G}$$ は次のように表せる。
$${G=\{id, g^1, g^2, g^3, \cdots g^n\}=\langle g \rangle}$$
ただし、$${n}$$ は $${0}$$ 以上の整数であり、$${g^0=id}$$(単位元) とします。
この巡回群 $${G}$$ は、次のように巡回します。
$$
\begin{align*}
&\;g^0(=id)\\
&\downarrow {\small g を作用}\\
&\;g^1\\
&\downarrow {\small g を作用}\\
&\;g^2\\
&\downarrow {\small g を作用}\\
&\;g^3\\
&\downarrow {\small g を作用}\\
&\hspace{4pt}\vdots\\
&\downarrow {\small g を作用}\\
&\;g^n\\
&\downarrow {\small g を作用}\\
&\;g^0(=id) {\small ここで id に戻る}
\end{align*}
$$
すると、$${G}$$ から任意の要素
$${g^j, g^k (\in G)}$$
を取ると、指数法則より
$${g^jg^k=g^{j+k}}$$
$${g^kg^j=g^{k+j}=g^{j+k}}$$
よって
$${g^jg^k=g^kg^j}$$
となるので、巡回群 $${G}$$ の任意の要素 $${g^j, g^k}$$ に対して交換法則が成り立つ。
(証明終)
例えば
$${g^2g^5=g^{2+5}=g^7}$$
$${g^5g^2=g^{5+2}=g^7}$$
より
$${g^2g^5=g^5g^2}$$
と、交換法則が成り立ちます。
なお、この定理の逆は成り立ちません。つまり
「可換群ならば巡回群である」
は成り立たないことを注意しておきます。
定理2 交換子についての定理
ここでやる「定理2」はかなり抽象的な定理なので、後に具体例を与えます。
ある群 $${G}$$ の正規部分群 $${H}$$ について、その $${H}$$ による剰余群 $${G/H}$$ を考えます。
ここで、剰余群 $${G/H}$$ について、次の定理が成り立ちます。
なお、「$${\in}$$」は要素として含むという記号です。
例 自然数の集合 $${\mathbb{N}=\{1, 2, 3, \cdots\}}$$ について、$${1 \in \mathbb{N}}$$、$${2 \in \mathbb{N}}$$、$${\cdots}$$
「定理2」
群 $${G}$$ の任意の要素 $${g_1, g_2}$$ について
$$
\begin{align*}
剰余群 G/H は可換群である \Longleftrightarrow g_1^{-1}g_2^{-1}g_1g_2 \in H
\end{align*}
$$
***
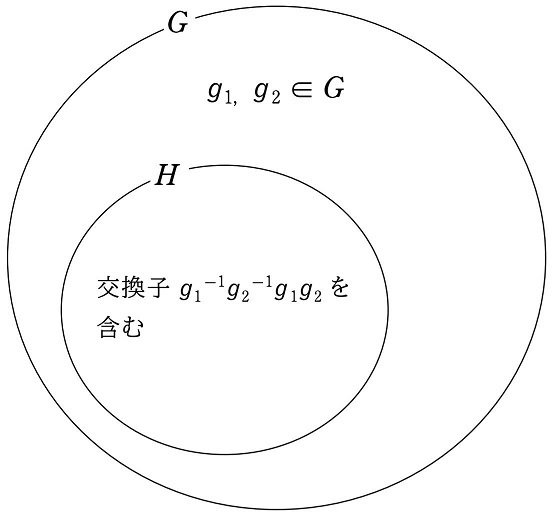
これは、剰余群 $${G/H}$$ が可換群になることと、任意の $${g_1, g_2 \in G}$$ に対して $${g_1^{-1}g_2^{-1}g_1g_2}$$ がすべて $${H}$$ に含まれる($${H}$$ の要素である)ことは同値であることを表しています。
この $${g_1^{-1}g_2^{-1}g_1g_2}$$ を、$${g_1}$$ と $${g_2}$$ の『交換子』といいます。
すでにやったように、$${g_1^{-1}}$$ は $${g_1}$$ の逆元、$${g_2^{-1}}$$ は $${g_2}$$ の逆元です。
ここで、上記の「すべて」という部分に注意してください。
任意の $${g_1, g_2 \in G}$$ に対して、交換子 $${g_1^{-1}g_2^{-1}g_1g_2}$$ が常に $${H}$$ の要素になることから、交換子 $${g_1^{-1}g_2^{-1}g_1g_2}$$ はすべて $${H}$$ に含まれることになります。何か $${g_1, g_2 \in G}$$ を選んで、交換子 $${g_1^{-1}g_2^{-1}g_1g_2}$$ を計算したら、それが $${H}$$ には入っていないことはあり得ないということです。
この「すべて」という表現は、証明の最後の部分まで関係してきますので、注意したい部分には「●」で強調していきます。
剰余群 $${G/H}$$ が可換群である$${\hspace{15pt}}$$
$${\hspace{5pt}\Updownarrow}$$ 同値
なお『同値』とは、2つの条件 $${p, q}$$ に対して
$${p ならば q}$$(これを $${p \Longrightarrow q}$$ と表記する)
と
$${q ならば p}$$(これを $${q \Longrightarrow p}$$ と表記する)
の両方が成り立つことで、このとき『$${p}$$ と $${q}$$ は同値である』といい
$${p \Longleftrightarrow q}$$
と表記します。
ここで、この「定理2」を証明します。
(証明)
ある群 $${G}$$ の正規部分群 $${H}$$ について、その $${H}$$ による剰余群 $${G/H}$$ を考えます。$${G/H}$$ の要素
$${g_1H, g_2H \in G/H}$$($${g_1, g_2}$$ は $${G}$$ の任意の要素)
について、$${G/H}$$ が可解群であることと交換法則
$${g_1H\circ g_2H=g_2H\circ g_1H}$$
が成り立つことは同値なので
$$
\begin{align*}
剰余群 G/H は可換群である
&\Leftrightarrow g_1H \circ g_2H=g_2H \circ g_1H\\
&\hspace{16pt}{\footnotesize 剰余類同士の演算 aH\!\!\circ\!bH\!\!=\!abH より}\\
&\Leftrightarrow g_1g_2H=g_2g_1H\\
&\hspace{16pt}{\footnotesize \Rightarrow 両辺に左から {g_2}^{-1} をかけて}\\
&\hspace{16pt}{\footnotesize \Leftarrow 両辺に左から g_2 をかけて}\\
&\Leftrightarrow {g_2}^{-1}g_1g_2H=\underset{e}{\underline{{g_2}^{-1}g_2}}g_1H\\
&\hspace{16pt}{\footnotesize {g_2}^{-1}g_2=e より}\\
&\Leftrightarrow {g_2}^{-1}g_1g_2H=\underset{g_1}{\underline{eg_1}}H\\
&\hspace{16pt}{\footnotesize eg_1=g_1 より}\\
&\Leftrightarrow {g_2}^{-1}g_1g_2H=g_1H\\
&\hspace{16pt}{\footnotesize \Rightarrow 両辺に左から {g_1}^{-1} をかけて}\\
&\hspace{16pt}{\footnotesize \Leftarrow 両辺に左から g_1 をかけて}\\
&\Leftrightarrow {g_1}^{-1}{g_2}^{-1}g_1g_2H=\underset{e}{\underline{{g_1}^{-1}g_1}}H\\
&\hspace{16pt}{\footnotesize {g_1}^{-1}g_1=e より}\\
&\Leftrightarrow {g_1}^{-1}{g_2}^{-1}g_1g_2H=eH\\
&\hspace{16pt}{\footnotesize eH=H より \cdots (*1)}\\
&\Leftrightarrow {g_1}^{-1}{g_2}^{-1}g_1g_2H=H\\
&\Leftrightarrow {g_1}^{-1}{g_2}^{-1}g_1g_2\in H \cdots (*2)\\
\end{align*}
$$
より
$$
\begin{align*}
剰余群 G/H は可換群である \Longleftrightarrow g_1^{-1}g_2^{-1}g_1g_2 \in H
\end{align*}
$$
(証明終)
ところどころで
$${{g_1}^{-1}g_1=g_1{g_1}^{-1}=e}$$($${{g_1}^{-1}}$$ は $${g_1}$$ の逆元なので)
$${{g_2}^{-1}g_2=g_2{g_2}^{-1}=e}$$($${{g_2}^{-1}}$$ は $${g_2}$$ の逆元なので)
$${eg_1=g_1}$$($${e}$$ は単位元なので)
$${eH=H \cdots (*1)}$$
$${{g_1}^{-1}{g_2}^{-1}g_1g_2H=H \Leftrightarrow {g_1}^{-1}{g_2}^{-1}g_1g_2\in H \cdots (*2)}$$
の関係式を利用しています。
ここで、分かりにくいと思われる $${(*1), (*2)}$$ を証明します。厳密な証明というより、具体例を上げての証明です。
$${(*1) eH=H}$$ の証明
$${eH}$$ とは、正規部分群 $${H}$$ の要素のすべてに左から単位元 $${e}$$ を作用させた剰余類です(本シリーズ (30))。仮に $${H}$$ を
$${H=\{e, h_2, h_3\}}$$
とすると($${H}$$ は群なので単位元 $${e}$$ を含みます)、単位元 $${e}$$ を作用せても変化しないこと
$${ee=e}$$
$${eh_2=h_2}$$
$${eh_3=h_3}$$
より
$$
\begin{align*}
eH&=e\{e, h_2, h_3\}\\
&=\{ee, eh_2, eh_3\}\\
&=\{e, h_2, h_3\}\\
&=H
\end{align*}
$$
よって、 $${eH=H}$$ となります。
$${(*2) {g_1}^{-1}{g_2}^{-1}g_1g_2H=H \Leftrightarrow {g_1}^{-1}{g_2}^{-1}g_1g_2\in H}$$ の証明
同値になることの証明なので、「$${\Rightarrow}$$」と「$${\Leftarrow}$$」を別々に証明します。
簡単のため、$${{g_1}^{-1}{g_2}^{-1}g_1g_2=g}$$ とおくと
$${gH=H \Leftrightarrow g\in H}$$
これを証明します。さらに、簡単のため
$${H=\{e, h_2, h_3\}}$$
とします(一般に要素を $${n}$$ 個としても証明は同じです)。$${H}$$ は群($${G}$$ の正規部分群)であるため、必ず単位元 $${e}$$ を含みます。
($${\Rightarrow}$$ の証明)
$${gH=H}$$ を仮定して $${g\in H}$$ になることを証明します。
正規部分群 $${H}$$ は単位元 $${e}$$ を含むので $${gH=H}$$ より
$$
\begin{align*}
gH&=g\{e, h_2, h_3\}\\
&=\{ge, gh_2, gh_3\}\\
&=\{g, gh_2, gh_3\}\\
&=H
\end{align*}
$$
$${e}$$ は単位元なので $${ge=g}$$ です。これより
$$
\begin{align*}
H=\{g, gh_2, gh_3\}
\end{align*}
$$
となるので、確かに $${H}$$ は要素として $${g}$$ を含んでいます。よって
$$
\begin{align*}
g\in H
\end{align*}
$$
($${\Leftarrow}$$ の証明)
$${g\in H}$$ を仮定して $${gH=H}$$ になることを証明します。
$${g\in H}$$ より、正規部分群 $${H}$$ は要素として $${g}$$ を含んでいます。$${H}$$ は群であるので、その $${g}$$ を $${H}$$ の要素すべてに作用させても、それは $${H}$$ 自身の要素です。つまり
$$
\begin{align*}
gH&=g\{e, h_2, h_3\}\\
&=\{ge, gh_2, gh_3\}\\
&=\{g, gh_2, gh_3\}\\
&\hspace{15pt}{\footnotesize g\in H より要素は H と同じ(順番が違うだけ)}\\
&=\{e, h_2, h_3\}\\
&=H
\end{align*}
$$
よって
$$
\begin{align*}
gH=H
\end{align*}
$$
以上により
$${gH=H \Leftrightarrow g\in H}$$
つまり
$${{g_1}^{-1}{g_2}^{-1}g_1g_2H=H \Leftrightarrow {g_1}^{-1}{g_2}^{-1}g_1g_2\in H}$$
が証明された。
交換子について具体例
この交換子について、具体的に例を上げてみます。
3次対称群
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
の正規部分群 $${N=\{id, \rho_2, \rho_3\}}$$ による剰余類は、次の2つのグループに分けられました(本シリーズ (30))。
$${idN=\rho_2N=\rho_3N=\{id, \rho_2, \rho_3\}}$$
$${\tau_1N=\tau_2N=\tau_3N=\{\tau_1, \tau_2, \tau_3\}}$$
すると、代表元として $${id, \tau_1}$$ を選ぶと、その剰余類の集合
$${S_3/N=\{idN, \tau_1N\}}$$
は
$${aH\circ bH=abH}$$
という演算に関して群(剰余群)であり、さらにそれは $${\tau_1N}$$ を生成元とする巡回群でもあり、次のように表記されます。
$${S_3/N=\{idN, \tau_1N\}=\langle \tau_1N \rangle}$$
すると「定理1」より「巡回群は可換群」なので
$${S_3/N=\{idN, \tau_1N\}=\langle \tau_1N \rangle}$$
は可換群となります。実際、次の群表
$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & idN & \tau_1N\\ \hline\hline
idN & idN & \tau_1N\\ \hline
\tau_1N & \tau_1N & idN
\end{array}
$$
より、$${idN, \tau_1N \in S_3/N}$$ について
$${idN\circ\tau_1N=\tau_1N\circ idN(=\tau_1N)}$$
となり、交換法則が成り立ちます。
さらに「定理2」より、$${S_3}$$ の任意の要素 $${g_1, g_2}$$ に対して
$$
\begin{align*}
剰余群 S_3/N は可換群である \Longleftrightarrow {g_1}^{-1}{g_2}^{-1}g_1g_2 \in N
\end{align*}
$$
より、交換子 $${g_1^{-1}g_2^{-1}g_1g_2}$$ は $${N}$$ の要素になります。
剰余群 $${S_3/N}$$ が可換群である$${\hspace{13pt}}$$
$${\hspace{5pt}\Updownarrow}$$ 同値

なお、$${g_1, g_2}$$ は $${N (\subset S_3)}$$ の要素である必要はなく、$${S_3}$$ から任意に選ぶことができます。
それでは、交換子 $${g_1^{-1}g_2^{-1}g_1g_2}$$ が $${N}$$ の要素になることを、具体例を上げて計算してみます。
$${S_3}$$ の要素として、仮に
$${g_1=\rho_2 (\in S_3)}$$
$${g_2=\tau_3 (\in S_3)}$$
を取ると(任意なので $${S_3}$$ から好きなものを選べる)、$${S_3}$$ の群表
$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c|c|c|c}
& id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3\\ \hline\hline
id & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3\\ \hline
\rho_2 & \rho_2 & \rho_3 & id & \tau_3 & \tau_1 & \tau_2\\ \hline
\rho_3 & \rho_3 & id & \rho_2 & \tau_2 & \tau_3 & \tau_1\\ \hline
\tau_1 & \tau_1 & \tau_2 & \tau_3 & id & \rho_2 & \rho_3\\ \hline
\tau_2 & \tau_2 & \tau_3 & \tau_1 & \rho_3 & id & \rho_2\\ \hline
\tau_3 & \tau_3 & \tau_1 & \tau_2 & \rho_2 & \rho_3 & id
\end{array}
$$
より
$${{\rho_2}^{-1}=\rho_3}$$($${\rho_2}$$ の逆元は $${\rho_3}$$)
$${{\tau_3}^{-1}=\tau_3}$$($${\tau_2}$$ の逆元は $${\tau_3}$$)
$${\rho_3\tau_3=\tau_1}$$
$${\tau_1\rho_2=\tau_2}$$
$${\tau_2\tau_3=\rho_2}$$
なので
$$
\begin{align*}
\underset{\rho_3}{\underline{{\rho_2}^{-1}}}\,\underset{\tau_3}{\underline{{\tau_3}^{-1}}}\,\rho_2\tau_3
&=\underset{\tau_1}{\underline{\rho_3\tau_3}}\rho_2\tau_3\\
&=\underset{\tau_2}{\underline{\tau_1\rho_2}}\tau_3\\
&=\underset{\rho_2}{\underline{\tau_2\tau_3}}\\
&=\rho_2 \in N
\end{align*}
$$
よって、交換子 $${{\rho_2}^{-1}{\tau_3}^{-1}\rho_2\tau_3}$$ は $${N}$$ に含まれます。なお、本シリーズでは置換は前から(左から)作用させていくと定義しています。
同様に考えることによって、$${S_3}$$ の任意の要素 $${g_1, g_2}$$ に対して、交換子 $${g_1^{-1}g_2^{-1}g_1g_2}$$ は $${N}$$ の要素になります。
補足1「定理2」に関する補足
ここで、先ほどの「定理2」
群 $${G}$$ の任意の要素 $${g_1, g_2}$$ について
$$
\begin{align*}
剰余群 G/H は可換群である \Longleftrightarrow g_1^{-1}g_2^{-1}g_1g_2 \in H
\end{align*}
$$
への補足を与えます。この定理の中の
$$
\begin{align*}
{g_1}^{-1}{g_2}^{-1}g_1g_2 \in H
\end{align*}
$$
という表現について、これは単に交換子
$${{g_1}^{-1}{g_2}^{-1}g_1g_2}$$
が $${H}$$ が含まれるという意味でなく、$${H}$$ は群 $${G}$$ の正規部分群(つまり群)であるので
「$${H}$$ は、交換子 $${{g_1}^{-1}{g_2}^{-1}g_1g_2}$$ 同士の積もすべて含んでいる」
ことに注意してください。
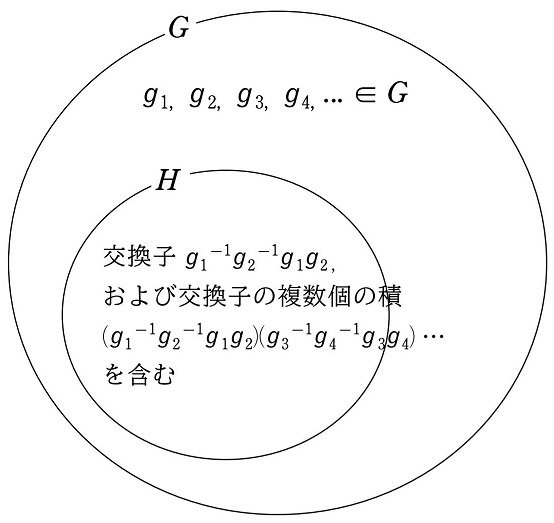
つまり、$${G}$$ の任意の要素 $${g_1, g_2, g_3, g_4}$$ について、$${{g_1}^{-1}{g_2}^{-1}g_1g_2}$$ と $${{g_3}^{-1}{g_4}^{-1}g_3g_4}$$ の交換子同士の積
$${\{{g_1}^{-1}{g_2}^{-1}g_1g_2\}\{{g_3}^{-1}{g_4}^{-1}g_3g_4\}}$$
も $${H}$$ は含んでいるということです。
剰余群 $${G/H}$$ が可換群である$${\hspace{15pt}}$$
$${\hspace{5pt}\Updownarrow}$$ 同値

なお、上図では2つの交換子の積ですが、3つでも4つでも、複数個つらなっていても問題ありません。(ひとつも含めて)交換子の複数個の積であれば、すべて $${H}$$ に含まれます。
$$
\begin{align*}
(交換子)\hspace{-7pt}(交換子)\cdots(交換子)\in H
\end{align*}
$$

以上のことを、後の証明で使いやすいように「補足1」としてまとめておきます。
「補足1」
定理2に関する補足として、$${G}$$ の任意の要素から作られる交換子、および交換子の複数個の積は、すべて $${H}$$ に含まれる。
***
定理3 任意の3次巡回置換は、3次巡回置換の交換子で表せる
ここで、交換子について次の定理があります。
「定理3」
任意の3次巡回置換は、3次巡回置換の交換子で表せる。
***
例えば、任意の3次巡回置換を $${(i j k)}$$ とします。$${i, j, k}$$ は任意の文字なので、例えば5次方程式の解 $${x_1, x_2, x_3, x_4, x_5}$$ などを自由に当てはめることができます。
すると、この $${(i j k)}$$ は、新しい文字 $${l, m}$$ を用いて次のように3次巡回置換の交換子として表すことができます。
$$
\begin{align*}
(i j k)={(k l i)}^{-1}{(j m i)}^{-1}(k l i)(j m i)
\end{align*}
$$
この式の右辺は交換子(3次巡回置換の交換子)になっていることに注意してください。上記の式について
$${g_1=(k l i)}$$
$${g_2=(j m i)}$$
とおくと
$$
\begin{align*}
(i j k)&={\underset{g_1}{\underline{(k l i)}}}^{-1}{\underset{g_2}{\underline{(j m i)}}}^{-1}\underset{g_1}{\underline{(k l i)}}\hspace{3pt}\underset{g_2}{\underline{(j m i)}}\\
&={g_1}^{-1}{g_2}^{-1}g_1g_2{\small(交換子)}
\end{align*}
$$
と、確かに交換子になります。
以下、この等式を証明しますが、その前に、巡回置換の逆元は、逆から並べることで表記できること、つまり
$$
\begin{align*}
{(k l i)}^{-1}=(i l k)
\end{align*}
$$
となることを先に証明します。
(証明)
巡回置換 $${(k l i)}$$
は
$${k \rightarrow l \rightarrow i \rightarrow k}$$
と巡回的に置き換える置換なので、丁寧に書くと次のようになります(本シリーズ (6))。
$$
\begin{align*}
(k l i)=
\begin{pmatrix}
k & l & i\\
l & i & k
\end{pmatrix}
\end{align*}
$$
上から下へ置き換えるとよみます。
すると、この逆元 $${{(k l i)}^{-1}}$$ は、先ほどの表記を上下に入れ替えたものです。つまり
$$
\begin{align*}
(k l i)&=
\begin{pmatrix}
k & l & i\\
l & i & k
\end{pmatrix}\\[10pt]
&\hspace{33pt}\updownarrow {\small 上下を入れ換える}\\[5pt]
{(k l i)}^{-1}&=
\begin{pmatrix}
l & i & k\\
k & l & i
\end{pmatrix}
\end{align*}
$$
上から下へを置き換えたものを、さらに下から上へと置き換えることによって元に戻ります。するとこれは
$${i \rightarrow l \rightarrow k \rightarrow i}$$
と巡回的に置き換える置換なので
$$
\begin{align*}
{(k l i)}^{-1}=
\begin{pmatrix}
l & i & k\\
k & l & i
\end{pmatrix}
=(i l k)
\end{align*}
$$
よって
$$
\begin{align*}
{(k l i)}^{-1}=(i l k)
\end{align*}
$$
となります。
(証明終)
それでは
$$
\begin{align*}
(i j k)={(k l i)}^{-1}{(j m i)}^{-1}(k l i)(j m i)
\end{align*}
$$
を証明します。
(証明)
先ほど証明したように、巡回置換の逆元は逆から並べればよいので
$${{(k l i)}^{-1}=(i l k)}$$
$${{(j m i)}^{-1}=(i m j)}$$
より
$$
\begin{align*}
(i j k)&={(k l i)}^{-1}{(j m i)}^{-1}(k l i)(j m i)\\
&=(i l k)(i m j)(k l i)(j m i) \cdots (*3)
\end{align*}
$$
ここからは、文字列
$${i j k l m}$$
に、$${(*3)}$$ の置換を左から順に作用させていきます。
なお、本シリーズでは置換の積は左から(前から)作用させると定義しているので
$$
\begin{align*}
(i j k)=\underset{➀}{(i l k)}\underset{➁}{(i m j)}\underset{➂}{(k l i)}\underset{➃}{(j m i)}
\end{align*}
$$
と $${➀}$$ ~ $${➃}$$ の順に作用させていくと
$$
\begin{alignat*}{5}
&i & &j & &k & &l & &m\\
& & & & &\hspace{-3pt}\downarrow & & & &\leftarrow \underset{➀}{(i l k)} を作用\\
&l & &j & &i & &k & &m\\
& & & & &\hspace{-3pt}\downarrow & & & &\leftarrow \underset{➁}{(i m j)} を作用\\
&l & &i & &\!m & &k & &j\\
& & & & &\hspace{-3pt}\downarrow & & & &\leftarrow \underset{➂}{(k l i)} を作用\\
&i & &k & &\!m & &l & &j\\
& & & & &\hspace{-3pt}\downarrow & & & &\leftarrow \underset{➃}{(j m i)} を作用\\
&j & &k & &i & &l & &m
\end{alignat*}
$$
最初と最後をつなげると
$$
\begin{alignat*}{5}
&i & &j & &k & &l & &m\\
& & & & &\hspace{-3pt}\downarrow & & & &\hspace{-20pt}\leftarrow {\footnotesize {(k l i)}^{-1}{(j m i)}^{-1}(k l i)(j m i) を作用}\\
&j & &k & &i & &l & &m
\end{alignat*}
$$
するとこれは
$${i \rightarrow j \rightarrow k \rightarrow i}$$
と巡回的に置き換える置換なので、これで
$$
\begin{align*}
(i j k)={(k l i)}^{-1}{(j m i)}^{-1}(k l i)(j m i)
\end{align*}
$$
が証明されました。
(証明終)
ここで重要なポイントは、この式を構成するには、$${i, j, k, l, m}$$ と5つの文字が必要だということです。例えば
$${i=x_1}$$
$${j=x_2}$$
$${k=x_3}$$
として3次巡回置換 $${(x_1 x_2 x_3)}$$ を考えると、この3つの文字だけでは交換子で表すことはできず、新しい文字
$${l=x_4}$$
$${m=x_5}$$
を加えて5つの文字を用いないと
$$
\begin{align*}
(x_1 x_2 x_3)={(x_3 x_4 x_1)}^{-1}{(x_2 x_5 x_1)}^{-1}(x_3 x_4 x_1)(x_2 x_5 x_1)
\end{align*}
$$
と交換子で表すことはできません。つまり、この文字を方程式の解とした場合、5つの解をもつ5次方程式でなければこの「定理3」は適用できないことになります。
この事実から、5次(以上の)方程式は、それより次数の低い2次、3次、4次方程式とは、解の置換の構造がまったく異なることが示唆されます。
この「定理3」は、5次以上の方程式には解の公式が存在しないこと証明に、決定的な役割を演じることになります。
ここで、遇置換について次の定理があります。
定理4 遇置換は3次巡回置換、および3次巡回置換の積で表すことができる
一般に、遇置換と3次巡回置換を結ぶ定理として、次の定理があります。
「定理4」
任意の遇置換は3次巡回置換、および3次巡回置換の複数個の積で表すことができる。
***
以下、この「定理4」を証明します。
(証明)
遇置換は偶数個の互換の積なので、たとえ何個も互換が連なっていても、次のように2つずつのセットで考えることができます。互換の積は偶数個なので、1個だけ残ることはありません。
$$
\begin{align*}
遇置換&=\underset{遇遇個の互換}{\underline{(* *)(* *)(* *)(* *)\hspace{5pt}\cdots\hspace{5pt}(* *)(* *)}}\\
&=\{\underset{2つセット}{\underline{(* *)(* *)}}\}\{\underset{2つセット}{\underline{(* *)(* *)}}\}\hspace{5pt}\cdots\hspace{5pt}\{\underset{2つセット}{\underline{(* *)(* *)}}\}
\end{align*}
$$
なお、一般に置換の積は交換法則は成り立ちます。交換法則は成り立つので、上記の様にカッコで区切っても問題ありません。しかし、交換法則は成り立たないので、置換の順番を入れ換えてはいけません。順番を入れ換えないでカッコで区切るのは大丈夫です。
ここで、互換の種類には次の2つの型があります。
(case1) 共通の文字を含むもの。
例 $${(x_1 x_2)(x_1 x_3)}$$
$${x_1}$$ が共通の文字です。
(case2) 共通の文字を含まないもの。
例 $${(x_1 x_2)(x_3 x_4)}$$
すべて異なる文字です。
(case1) の型は、次のように3次巡回置換で表すことができます(本シリーズ (16))。
$$
\begin{align*}
(\underline{x_1} x_2)(\underline{x_1} x_3)=(\underline{x_1} x_2 x_3)
\end{align*}
$$
各々の最初にある共通の文字 $${x_1}$$(下線部)を先頭に、$${x_2}$$, $${x_3}$$ と順に並べていきます。これは、次のような形式で公式化できます。
$$
\begin{align*}
(〇 ♠)(〇 ♣)=(〇 ♠ ♣) \cdots(公式1)
\end{align*}
$$
$${〇}$$を先頭にして、赤矢印の順に文字を並べていきます。

(case2) の型は、次のように3次巡回置換の積で表すことができます(本シリーズ (16))。
$$
\begin{align*}
(x_1 x_2)(x_3 x_4)&=(x_1 x_3 x_2)(x_2 x_4 x_3)
\end{align*}
$$
これは、次のような形式で公式化できます。
$$
\begin{align*}
(〇 ♠)(△ ♣)&=(〇 △ ♠)(♠ ♣ △) \cdots(公式2)
\end{align*}
$$
赤矢印、青矢印の順に、文字を拾いながら並べていきます。

2つの互換の積は (case1) と (case2) の、必ずどちらかの型になるので、この2つの公式を用いることによって、任意の遇置換を3次巡回置換、または3次巡回置換の複数個の積であらわすことができます。
(証明終)
具体例をあげてみます。
例えば、次のような遇置換があったとします。
$$
\begin{align*}
(x_1 x_2)(x_4 x_1)(x_1 x_2)(x_4 x_5)
\end{align*}
$$
これは互換が4個(偶数個)なので遇置換です。これを、前2つと後ろ2つの2つのブロックに分けます。
$$
\begin{align*}
\{(x_1 x_2)(x_4 x_1)\}\{(x_1 x_2)(x_4 x_5)\}
\end{align*}
$$
前2つについては、互換は順番を入れ換えても同じ、つまり
$${(x_4 x_1)=(x_1 x_4)}$$
なので、(公式1)を用いて
$$
\begin{align*}
(x_1 x_2)(x_4 x_1)&=(x_1 x_2)(x_1 x_4)\\
&=(x_1 x_2 x_4)
\end{align*}
$$
後ろ2つについては、(公式2)を用いて
$$
\begin{align*}
(x_1 x_2)(x_4 x_5)&=(x_1 x_4 x_2)(x_2 x_5 x_4)
\end{align*}
$$
まとめると
$$
\begin{align*}
&(x_1 x_2)(x_4 x_1)(x_1 x_2)(x_4 x_5)\\
=\,&\{(x_1 x_2)(x_4 x_1)\}\{(x_1 x_2)(x_4 x_5)\}\\
=\,&\{(x_1 x_2)(x_1 x_4)\}\{(x_1 x_2)(x_4 x_5)\}\\
=\,&(x_1 x_2 x_4)(x_1 x_4 x_2)(x_2 x_5 x_4)
\end{align*}
$$
となり、遇置換を3次巡回置換の積で表すことができました。
ここで、後のために部分集合について復習します(本シリーズ (29))。
部分集合の定義(復習)
例えば、2つの集合
$${\text{P}=\{2, 4\}}$$
$${\text{Q}=\{1, 2, 3, 4, 5\}}$$
では、どの $${\text{P}}$$ の要素もまた $${\text{Q}}$$ の要素になっています。つまり
$${\text{P}}$$ の要素 $${2}$$ は $${\text{Q}}$$ の要素になっている。
$${\text{P}}$$ の要素 $${4}$$ は $${\text{Q}}$$ の要素になっている。
この2つの集合の関係を図で描くと、次のようになります。

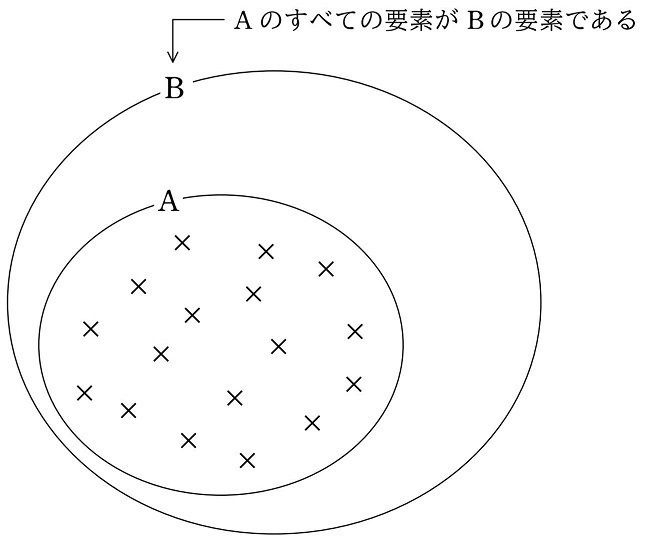
一般に、2つの集合 $${\text{A}}$$、$${\text{B}}$$ において、$${\text{A}}$$ のどの要素もまた $${\text{B}}$$ の要素であるとき
$$
\begin{align*}
\text{A}\subseteqq\text{B}
\end{align*}
$$
と表します。このとき、$${\text{A}}$$ は $${\text{B}}$$ の部分集合といいます。
ここで重要なのは、上記の黒字「どの要素もまた」という部分です。$${\text{A}}$$ のすべての要素がひとつ残らず $${\text{B}}$$ の要素であるとき
$$
\begin{align*}
\text{A}\subseteqq\text{B}
\end{align*}
$$
となります。

表記上の注意
なお蛇足として、イコールを含めないで
$$
\begin{align*}
\text{A}\subset\text{B}
\end{align*}
$$
と表記する場合もあります。
$${\text{A}\subset\text{B}}$$
はイコールになる場合、つまり
$${\text{A}=\text{B}}$$
の場合も含んでいます。よって、(特につける必要はないですが)イコールになる場合も強調したいときは
$${\text{A}\subseteqq\text{B}}$$
と、イコールをつけて表記する場合もあります。
真部分集合
また、イコールを含まない場合は
$${\text{A}\subsetneqq\text{B}}$$
と、$${\ne}$$ をつけて表記する場合もあります。
このとき $${\text{A}}$$ は $${\text{B}}$$ の『真部分集合』といいます。平たくいえば、真部分集合とは
「もとの集合の一部だけど、もとの集合(自分自身)とは異なる集合」
です。例えば、集合 $${\{1, 2, 3\}}$$ の部分集合は全部で
$${\phi}$$(空集合)
$${\{1\}}$$
$${\{2\}}$$
$${\{3\}}$$
$${\{1, 2\}}$$
$${\{2, 3\}}$$
$${\{1, 3\}}$$
$${\{1, 2, 3\}}$$
の8通りがありますが、$${\{1, 2, 3\}}$$ の真部分集合は、自分自身を除いた
$${\phi}$$(空集合)
$${\{1\}}$$
$${\{2\}}$$
$${\{3\}}$$
$${\{1, 2\}}$$
$${\{2, 3\}}$$
$${\{1, 3\}}$$
の7通りです。
5次対称群のガロア対応
いよいよここから証明の本丸に入ります。証明すべき命題は
「5次対称群 $${S_5}$$ は可解群ではない」
ということです。
まず、5次方程式の5つの解を
$${x_1, x_2, x_3, x_4, x_5}$$
とすると、その5つの解の置換を5次置換といいます(本シリーズ (14))。5次置換は全部で
$${5\times4\times3\times3\times1=120}$$ 通り
あります。この5次置換をすべた集めた集合は積に関して群になり、その群を5次対称群 $${S_5}$$ といいます。
さらに、5次置換は遇置換と奇置換に分かれます。ちょうど半分、同じ数ずつ別れるので、遇置換は $${60}$$ 通り、奇置換は $${60}$$ 通りです(注2)(本シリーズ (15))。
その $${60}$$ 通りある遇置換をすべて集めたものも群となり、それを5次交代群 $${A_5}$$ といいます。
さて、5次交代群 $${A_5}$$ は5次対称群 $${S_5}$$ の正規部分群です。すると、$${S_5}$$ の $${A_5}$$ による剰余類の集合 $${S_5/A_5}$$ は要素が2つの剰余群になり、さらにそれは巡回群にもなります。ここまでは3次対称群と同じです。
一般に、$${n}$$ 次対称群 $${S_n}$$ の正規部分群である $${n}$$ 次交代群 $${A_n}$$(遇置換のみを集めた正規部分群)について、その $${A_n}$$ による剰余群 $${S_n/A_n}$$ は、要素が2つの巡回群になります(証明は割愛)。
(例)
$${S_3/N=\underset{要素が2つ}{\{idN, \tau_1N\}}=\langle\tau_1N\rangle}$$ は要素が2つの巡回群(本シリーズの証明では $${A_3=N}$$ としている)
$${S_4/A_3}$$ は要素が2つの巡回群
$${S_5/A_5}$$ は要素が2つの巡回群
$${S_6/A_6}$$ は要素が2つの巡回群
以下同様。
すると、ここまでの5次方程式についての「体の拡大」と「群の縮小」との対応関係(ガロア対応)は下図のようになります。
$$
\begin{align*}
&\hspace{5pt}{\footnotesize X_5 を添加}\\[-4pt]
&\hspace{19pt}\downarrow\\[-2pt]
{\small \bm{<体の拡大>}}\hspace{10pt}&\hspace{-5pt}{\scriptsize Q_5(\omega_5)}\hspace{-2pt}\overset{\bm{拡大}}{\subset}\hspace{-2pt}{\scriptsize Q_5(\omega_5, X_5)}\\[-3pt]
&\hspace{19pt}\Updownarrow\hspace{1pt}{\footnotesize 対応}\\[-2pt]
{\small \bm{<群の縮小>}}\hspace{10pt}&S_5\hspace{5pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_5 の正規部分群}{A_5}\\[-4pt]
&\hspace{19pt}\uparrow\\[-3pt]
&\hspace{8pt}{\footnotesize S_5/A_5 \atop が巡回群}
\end{align*}
$$
以下、この対応関係について解説します。流れは3次方程式のときと同じです(本シリーズ (37))。
まず、一般の5次方程式
$${ax^5+bx^4+cx^3+dx^2+ex+f=0}$$
の係数 $${a, b, c, d, e, f}$$ と有理数、および $${1}$$ の5乗根(5乗して $${1}$$ になる数)のうち複素数となる定数 $${\omega_5}$$ との加減乗除で閉じた体(基礎体)を
$${Q_5(\omega_5)}$$
とします。基礎体とは拡大する前の最初の体です。
すると、$${Q_5(\omega_5)}$$ は(5変数の)すべての対称式の集合となります。

証明は省きますが、3次方程式のときにやった $${Q_3(\omega)}$$ が(3変数の)対称式の集合になることと同様の理由です(本シリーズ (37) の(注2))。
この $${Q_5(\omega_5)}$$ 内で構成される式は、$${120}$$ 通りある5次置換のすべてで変化しません。

よって、$${Q_5(\omega_5)}$$ 内で構成されるすべての式を変化させない群として、5次対称群 $${S_5}$$ が対応します。
次に、一般の5次方程式 $${ax^5+bx^4+cx^3+dx^2+ex+f=0}$$ の解
$${x_1, x_2, x_3, x_4, x_5}$$
の差積
$$
\begin{align*}
X_5=(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&
\end{align*}
$$
を考えます。この差積 $${X_5}$$ は、遇置換を作用させても変化しません。つまり遇置換シンメトリーをもちます(本シリーズ (14))。
一般に、何次であっても差積(解の差をすべてかけたもの)は遇置換で変化せず、遇置換シンメトリーをもちます。
$${X_2=\alpha-\beta}$$ は遇置換で変化しない
$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$ は遇置換で変化しない
以下同様に、$${X_4, X_5, X_6, \cdots}$$ はすべて遇置換で変化しない。
この差積 $${X_5}$$ について、その2乗 $${{\left(X_5\right)}^2}$$ は対称式なので、体 $${Q_5(\omega_5)}$$ 内で構成できます。しかし、差積そのもの $${X_5}$$ は $${Q_5(\omega_5)}$$ 内で構成できません。

そこで、$${Q_5(\omega_5)}$$ に差積 $${X_5}$$ を添加して体を拡大します。その拡大された拡大体を
$${Q_5(\omega_5, X_5)}$$
とします。

添加された差積 $${X_5}$$ は遇置換で変化しないので、体 $${Q_5(\omega_5, X_5)}$$ 内の加減乗除で構成されるすべての式は、遇置換で変化しません。つまり、遇置換シンメトリーをもちます。

すると、$${S_5}$$ の要素のうち、遇置換だけをすべて集めた群は5次交代群 $${A_5}$$ であったので、拡大体 $${Q_5(\omega_5, X_5)}$$ と $${A_5}$$ が対応します。
これで、「体の拡大」と「群の縮小」の対応関係が生まれます。
$$
\begin{align*}
{\small \bm{<体の拡大>}}\hspace{10pt}&\hspace{-5pt}{\scriptsize Q_5(\omega_5)}\hspace{-2pt}\overset{\bm{拡大}}{\subset}\hspace{-2pt}{\scriptsize Q_5(\omega_5, X_5)}\\[-3pt]
&\hspace{19pt}\Updownarrow\hspace{1pt}{\footnotesize 対応}\\[-2pt]
{\small \bm{<群の縮小>}}\hspace{10pt}&S_5\hspace{5pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_5 の正規部分群}{A_5}
\end{align*}
$$
しかしこれだけだとただ対応させているだけなので、この拡大と縮小の対応関係を、群構造の面から補強します。それが次に述べる「剰余群が巡回群になる」ことです。
$${S_5}$$ の $${A_5}$$ による剰余類の集合 $${S_5/A_5}$$ は剰余群となり、さらにそれは巡回群となります。
すると、差積 $${X_5}$$ は「2」乗すると対称式です。また、巡回群 $${S_5/A_5}$$ は要素の数が「2」つの巡回群です。「2」という共通項が見られます(なお、本シリーズ (37) でやった差積 $${X_3}$$ と巡回群 $${S_3/N}$$ も「2」という共通項でした)。
これにより、「差積 $${X_5}$$ の添加」と「剰余群 $${S_5/A_5}$$ が巡回群になること」とに対応関係を見出すことができ、次のようにガロア対応を構成することができます。
$$
\begin{align*}
&\hspace{5pt}{\footnotesize X_5 を添加}\\[-4pt]
&\hspace{19pt}\downarrow\\[-2pt]
{\small \bm{<体の拡大>}}\hspace{10pt}&\hspace{-5pt}{\scriptsize Q_5(\omega_5)}\hspace{-2pt}\overset{\bm{拡大}}{\subset}\hspace{-2pt}{\scriptsize Q_5(\omega_5, X_5)}\\[-3pt]
&\hspace{19pt}\Updownarrow\hspace{1pt}{\footnotesize 対応}\\[-2pt]
{\small \bm{<群の縮小>}}\hspace{10pt}&S_5\hspace{5pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_5 の正規部分群}{A_5}\\[-4pt]
&\hspace{19pt}\uparrow\\[-3pt]
&\hspace{8pt}{\footnotesize S_5/A_5 \atop が巡回群}
\end{align*}
$$
方程式に解の公式が存在するかどうかは、このガロア対応の群の縮小構造に着目します。剰余群が巡回群になるような正規部分群をとりながら、5次対称群 $${S_5}$$ が $${I=\{id\}}$$ まで縮小していくかどうか、つまり $${S_5}$$ が可解群になるかどうかに着目します(本シリーズ (36), (37))。
「$${S_5}$$ が可解群であれば、5次方程式に解の公式が存在する」
「$${S_5}$$ が可解群でなければ、5次方程式に解の公式は存在しない」
ということです。
実際は、$${S_5}$$ は可解群ではないので、5次方程式に解の公式は存在しません。以下、その証明です。
(最終目標)5次対称群が可換群ではないことの証明
今の段階で、群を $${S_3}$$ から $${A_5}$$ まで縮小することができました。これが最初のステージです。これを<ステージ1>とよぶことにします。
$$
\begin{align*}
&\hspace{-4pt}{\footnotesize \bm{<ステージ1>}}\\
{\small \bm{<群の縮小>}}\hspace{10pt}&S_5\hspace{4pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_5 の正規部分群}{A_5}\\[-4pt]
&\hspace{18.5pt}\uparrow\\[-3pt]
&\hspace{7pt}{\footnotesize S_5/\hspace{-1pt}A_5 \atop が巡回群}
\end{align*}
$$
すると、$${S_5}$$ が可解群であるためには
「$${A_5}$$ の正規部分群 $${M}$$ による剰余群 $${A_5/M}$$ が巡回群となりながら、正規部分群をさらに $${M (\subset A_5)}$$ に縮小できる」
ことになります。これを<ステージ2>とよぶことにします。
$$
\begin{align*}
&\hspace{-7pt}{\footnotesize \bm{<ステージ1>}}\hspace{0pt}{\footnotesize \bm{<ステージ2>}}\\
{\small \bm{<群の縮小>}}\hspace{10pt}&S_5\hspace{5pt}\overset{\bm{縮小}}{\supset}\hspace{-6pt}\underset{\tiny S_5 の正規部分群}{A_5}\hspace{-6pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny A_5 の正規部分群}{M}\\[-4pt]
&\hspace{19pt}\uparrow\hspace{40pt}\uparrow\\[-2pt]
&\hspace{7pt}{\footnotesize S_5/A_5 \atop が巡回群}\hspace{10pt}{\footnotesize A_5/M \atop が巡回群}
\end{align*}
$$
なお、縮小なので
$$
\begin{align*}
A_5\ne M
\end{align*}
$$
であることに注意してください。
$${A_5}$$ の正規部分群には自分自身 $${A_5}$$ も含みますが、$${M}$$ は $${A_5}$$ に等しいものではなく、 要素の数がより小さい正規部分群でなくてはなりません。等しくならないことを強調するために、含まれるが等しくはない「$${\supsetneqq}$$」という記号を用いれば、ガロア対応を次のように表記し直すことができます。
$$
\begin{align*}
&\hspace{-7pt}{\footnotesize \bm{<ステージ1>}}\hspace{0pt}{\footnotesize \bm{<ステージ2>}}\\
{\small \bm{<群の縮小>}}\hspace{10pt}&S_5\hspace{5pt}\overset{\bm{縮小}}{\supsetneqq}\hspace{-5pt}\underset{\tiny S_5 の正規部分群}{A_5}\hspace{-6pt}\overset{\bm{縮小}}{\supsetneqq}\hspace{-6pt}\underset{\tiny A_5 の正規部分群}{M}\\[-4pt]
&\hspace{19pt}\uparrow\hspace{42pt}\uparrow\\[-2pt]
&\hspace{7pt}{\footnotesize S_5/A_5 \atop が巡回群}\hspace{12pt}{\footnotesize A_5/M \atop が巡回群}
\end{align*}
$$
$${S_5}$$ が可解群であれば、<ステージ2>をもクリアし、最終的に $${I=\{id\}}$$ まで正規部分群が縮小されるはずです。
$$
\begin{align*}
&\hspace{-7pt}{\footnotesize \bm{<ステージ1>}}\hspace{0pt}{\footnotesize \bm{<ステージ2>}}\\
{\small \bm{<群の縮小>}}\hspace{10pt}&S_5\hspace{5pt}\overset{\bm{縮小}}{\supsetneqq}\hspace{-5pt}\underset{\tiny S_5 の正規部分群}{A_5}\hspace{-6pt}\overset{\bm{縮小}}{\supsetneqq}\hspace{-6pt}\underset{\tiny A_5 の正規部分群}{M}\hspace{-6pt}\overset{\bm{縮小}}{\supsetneqq}\hspace{6pt}\cdots \hspace{6pt}\overset{\bm{縮小}}{\supsetneqq}I\\[-4pt]
&\hspace{19pt}\uparrow\hspace{42pt}\uparrow\hspace{40pt}\uparrow\hspace{38pt}\uparrow\\[-2pt]
&\hspace{7pt}{\footnotesize S_5/A_5 \atop が巡回群}\hspace{12pt}{\footnotesize A_5/M \atop が巡回群}\hspace{10pt}{\footnotesize M/? \atop が巡回群}\hspace{10pt}{\footnotesize ?/I \atop が巡回群}
\end{align*}
$$
そこで、証明は背理法を用います。背理法は
「ある命題が正しいと仮定し、論理的に矛盾を導き出すことによって、その命題が正しくないと結論する証明法」
です(注1で詳解)。
背理法による証明
(証明)
5次対称群 $${S_5}$$ が可解群であると仮定します。背理法の仮定です。
<ステージ1>はクリアできたので、可解群であるならば、先ほど述べた<ステージ2>
「$${A_5}$$ の正規部分群 $${M}$$ による剰余群 $${A_5/M}$$ が巡回群となりながら、正規部分群をさらに $${M (\subsetneqq A_5)}$$ に縮小できる」
ことになります。
$$
\begin{align*}
&\hspace{-7pt}{\footnotesize \bm{<ステージ1>}}\hspace{0pt}{\footnotesize \bm{<ステージ2>}}\\
{\small \bm{<群の縮小>}}\hspace{10pt}&S_5\hspace{5pt}\overset{\bm{縮小}}{\supsetneqq}\hspace{-5pt}\underset{\tiny S_5 の正規部分群}{A_5}\hspace{-6pt}\overset{\bm{縮小}}{\supsetneqq}\hspace{-6pt}\underset{\tiny A_5 の正規部分群}{M}\\[-4pt]
&\hspace{19pt}\uparrow\hspace{42pt}\uparrow\\[-2pt]
&\hspace{7pt}{\footnotesize S_5/A_5 \atop が巡回群}\hspace{12pt}{\footnotesize A_5/M \atop が巡回群}
\end{align*}
$$
あらためて、$${M}$$ と $${A_5}$$ の包含関係は
$$
\begin{align*}
M \subsetneqq A_5 \cdots (*4)
\end{align*}
$$
であることに注意してください。後に使うので、これを $${(*4)}$$ とします。
まず、$${A_5/M}$$ は巡回群なので
「定理1」
巡回群は可換群である。
より、$${A_5/M}$$ は可換群となります。次に
「定理2」
群 $${G}$$ の任意の要素 $${g_1, g_2}$$ について
$$
\begin{align*}
剰余群 G/H は可換群である \Longleftrightarrow g_1^{-1}g_2^{-1}g_1g_2 \in H
\end{align*}
$$
より、群 $${A_5}$$ の任意の要素 $${g_1, g_2}$$ について
$$
\begin{align*}
剰余群 A_5/M は可換群である \Longleftrightarrow g_1^{-1}g_2^{-1}g_1g_2 \in M
\end{align*}
$$
が成り立ちます。「定理2」について、$${G}$$ を $${A_5}$$ に、$${H}$$ を $${M}$$ に置き換えたものです。
剰余群 $${A_5/M}$$ が可換群である$${\hspace{5pt}}$$
$${\hspace{15pt}\Updownarrow}$$ 同値

すると、$${A_5/M}$$ は可換群であるので
$${g_1^{-1}g_2^{-1}g_1g_2 \in M}$$
が常に成り立ちます。$${A_5}$$ の任意の要素 $${g_1, g_2 (\in A_5)}$$ から作られる交換子 $${g_1^{-1}g_2^{-1}g_1g_2}$$ は、すべて $${M}$$ に含まれることになります。この事実を、次にようにまとめておきます。
「$${A_5}$$ の任意の要素 $${g_1, g_2}$$ から作られる交換子 $${g_1^{-1}g_2^{-1}g_1g_2}$$ は、すべて $${M}$$ に含まれる」
すると、「定理2」に関する「補足1」
「補足1」
定理2に関する補足として、$${G}$$ の任意の要素から作られる交換子、および交換子の複数個の積は、すべて $${H}$$ に含まれる。
より、次のことがいえます。後に重要になるので、これを $${(*5)}$$ としてまとめておきます。
「$${A_5}$$ の任意の要素から作られる交換子、および交換子の複数個の積は、すべて $${M}$$ に含まれる」$${\cdots (*5)}$$

「補足1」について、$${G}$$ を $${A_5}$$ に、$${H}$$ を $${M}$$ に置き換えたものです。
5次交代群について
さてここで、5次交代群 $${A_5}$$ について考えます。
$${A_5}$$ は $${S_5}$$ から遇置換のみを集めた群です(注2)。つまり $${A_5}$$ のすべての要素は遇置換となります。すると
「定理4」
任意の遇置換は3次巡回置換、または3次巡回置の複数個の積で表すことができる。
より、$${A_5}$$ のすべての要素は3次巡回群、または3次巡回群の複数個の積で表すことができます(注3)。

さらに
「定理3」
任意の3次巡回置換は、3次巡回置換の交換子で表せる。
$$
\begin{align*}
(i j k)={(k l i)}^{-1}{(j m i)}^{-1}(k l i)(j m i)
\end{align*}
$$
より、$${A_5}$$ のすべて要素は、$${A_5}$$ の要素(3次巡回置換)から作られる交換子、および交換子の複数個の積で表すことができます。

これで、$${A_5}$$ のすべての要素は、$${A_5}$$ 自身の要素(3次巡回置換)から作られる交換子で表せることが分かりました。
すると、先に示した $${(*5)}$$
「$${A_5}$$ の任意の要素から作られる交換子、および交換子の複数個の積は、すべて $${M}$$ に含まれる」$${\cdots (*5)}$$
より、$${A_5}$$ のすべての要素($${A_5}$$ の要素から作られる交換子、および交換子の複数個の積)は、ひとつ残らず $${M}$$ に含まれることになります。

$${A_5}$$ の要素の中に、$${M}$$ に含まれない要素があってはいけない。つまり下図のようにはなりません。

よって、先に述べた「部分集合の定義」により
$$
\begin{align*}
A_5 \subseteqq M \cdots (*6)
\end{align*}
$$
が示されます。

(復習)部分集合の定義
$${\text{A}}$$ のすべての要素がひとつ残らず $${\text{B}}$$ の要素であるとき
$$
\begin{align*}
\text{A}\subseteqq\text{B}
\end{align*}
$$
***
この部分集合の定義において、$${A}$$ を $${A_5}$$ に、$${B}$$ を $${M}$$ に置き換えたのが
$$
\begin{align*}
A_5 \subseteqq M \cdots (*6)
\end{align*}
$$
になります。
つまり、$${A_5}$$ は $${M}$$ の部分集合です。$${A_5=M}$$ になる場合も含んでいます。
しかしこれは矛盾です。
背理法の仮定「$${S_5}$$ は可解群である」より、$${M}$$ は $${A_5}$$ の正規部分群であり、かつ等しくないので
$$
\begin{align*}
M \subsetneqq A_5 \cdots (*4)
\end{align*}
$$
であることは、背理法の証明の最初の方で述べました。つまり、$${(*4)}$$ と $${(*6)}$$
$$
\begin{align*}
M &\subsetneqq A_5 \cdots (*4)\\
A_5 &\subseteqq M \cdots (*6)
\end{align*}
$$
は同時に成り立ちません。
$${(*4)}$$ は、$${M}$$ が $${A_5}$$ の真部分集合であることを表しています。真部分集合なので、等しい場合は含みません。

$${(*6)}$$ は、$${A_5}$$ が $${M}$$ の真部分集合($${A_5\subsetneqq M}$$)か、または等しいこと($${A_5=M}$$)を表しています。
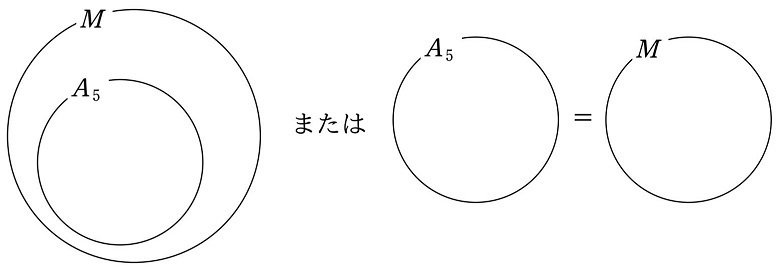
よって、$${(*4)}$$ と $${(*6)}$$ は同時に成り立たないので矛盾です。この矛盾によって、背理法の仮定である
「5次対称群 $${S_5}$$ は可解群である」
が間違いであることになり、これで
「5次対称群 $${S_5}$$ は可解群ではないこと」
つまり
「5次方程式に解の公式が存在しないこと」
が証明されました。
(証明終)
結局のところ、 $${S_5}$$ の正規部分群の縮小は $${A_5}$$ までで、それ以上は縮小できないということです。$${I=\{id\}}$$ まで縮小できないので、$${S_5}$$ は可解群ではありません。
6次以上の方程式の場合はどうか?
6次方程式には6つの解 $${x_1, x_2, x_3, x_4, x_5, x_6}$$ があります。すると、解(を表す文字)が6つあるので 、そのうちの5つを選んで「定理3」の交換子表示
$$
\begin{align*}
(i j k)={(k l i)}^{-1}{(j m i)}^{-1}(k l i)(j m i)
\end{align*}
$$
が適用できるようになり、本記事と同じ議論で
「6次対称群 $${S_6}$$ は可解群ではないこと」
証明されます。同様にして、7次以上の方程式についても同じ議論が適用できるので、それによって
「$${n}$$ 次対称群 $${S_n}$$ は可解群ではないこと($${n\geqq5}$$)」
が証明され、これで「5次以上の方程式には解の公式が存在しない」ことが証明されます。
追記(まとめ)証明の急所はどこか?
証明の急所は、「定理3」である次の等式
$$
\begin{align*}
(i j k)={(k l i)}^{-1}{(j m i)}^{-1}(k l i)(j m i)
\end{align*}
$$
にあります。
「任意の3次巡回置換は、3次巡回置換の交換子で表すことができる」
という等式です。すでに解説しましたが、この式を構成するには、$${i, j, k, l, m}$$ と5つの文字が必要です。例えば
$${i=x_1}$$
$${j=x_2}$$
$${k=x_3}$$
として3つの解(を表す文字)の3次巡回置換
$${(i j k)=(x_1 x_2 x_3)}$$
を考えると、この3つの解だけでは交換子で表すことはできず、新しい解
$${l=x_4}$$
$${m=x_5}$$
を加えて5つの解を用いないと
$$
\begin{align*}
(x_1 x_2 x_3)={(x_3 x_4 x_1)}^{-1}{(x_2 x_5 x_1)}^{-1}(x_3 x_4 x_1)(x_2 x_5 x_1)
\end{align*}
$$
と交換子で表すことはできない。つまり、5次以上の方程式に関して、この「定理3」の等式を用いた証明は適用されることになります。
すると、背理法の仮定「5次対称群 $${S_5}$$ が可解群である」より
$$
\begin{align*}
M \subsetneqq A_5 \cdots (*4)
\end{align*}
$$
であったものが、「定理3」の等式
$$
\begin{align*}
(x_1 x_2 x_3)={(x_3 x_4 x_1)}^{-1}{(x_2 x_5 x_1)}^{-1}(x_3 x_4 x_1)(x_2 x_5 x_1)
\end{align*}
$$
を用いることによって
$$
\begin{align*}
A_5 \subseteqq M \cdots (*6)
\end{align*}
$$
が導き出され、$${(*4)}$$ と $${(*6)}$$ は同時に成り立たないので矛盾が生じる。よって、背理法の仮定は間違いであること、つまり
「5次対称群 $${S_5}$$ は可解群ではない」
ことが証明され
「5次方程式には解の公式が存在しない」
と帰結される、というのが本記事の証明の核心です。
終わりに
以上で「群」を用いることによって、5次以上の方程式に解の公式が存在しないことが証明されました。
証明の方法は、他にもいろいろな方法があるようです。例えば、$${A_5}$$ の正規部分群は、自分自身 と $${\{id\}}$$ のみであることを示す方法や、交換子群(交換子で生成される群)を用いる方法もあるようです。
本シリーズでは、なるべく専門的な数学の言葉を使わないで、イメージしやすいと思った道筋で証明を進めたために、数学的に不十分なところがあると思います。
メインの部分はこの章で終わりとなりますが、必要があれば(時間の許す範囲内で)補足として次の章から拾い上げていきます。
(注1)『背理法』について(復習)
『背理法』とは、「ある命題の結論が正しいことを証明するために、その結論の否定を仮定して、すでに真であるとわかっている事実や元の命題の仮設などに矛盾することから、その命題の結論が正しいことを証明する方法」
例えば次の命題を背理法で証明しましょう。
命題『ある整数 $${n}$$ について $${n^2}$$ が偶数であるとする。このとき $${n}$$ は偶数である。』
(証明)
この命題の結論は「$${n}$$ は偶数である」。この結論の否定、つまり「$${n}$$ は奇数である」と仮定する(背理法の仮定)。$${n}$$ は奇数なので、$${k}$$ を $${0}$$ 以上の整数 ($${0, 1, 2, 3, \cdots}$$) として $${n=2k+1}$$ とおける *。
ここで展開公式
$${(a+b)^2=a^2+2ab+b^2}$$
を用いると
$$
\begin{align*}
n^2&=(2k+1)^2\\
&=(2k)^2+2\cdot2k\cdot1+1^2\\
&=4k^2+4k+1\\
&=2(2k^2+2k)+1\\
&=2l+1 (ただし l=2k^2+2k とおいた)
\end{align*}
$$
すると、$${k}$$ は $${0}$$ 以上の整数であることから、$${l(=2k^2+2k)}$$ も $${0}$$ 以上の整数となるので、 $${2l+1}$$ は奇数である*。これは $${n^2}$$ が偶数であるという条件(元の命題の仮設)に矛盾しているので、これによって背理法の仮定「$${n}$$ は奇数である」が正しくないこと、つまり「$${n}$$ は偶数である」ことが証明された。(証明終)
*奇数 $${1, 3, 5, 7, \cdots}$$ は
$${1=2\times0+1}$$
$${3=2\times1+1}$$
$${5=2\times2+1}$$
$${7=2\times3+1}$$
$${\hspace{23pt}\vdots}$$
より、$${n=2k+1}$$($${k}$$ は $${0}$$ 以上の整数)の形で書ける。
ここで5次置換を遇置換と奇置換に分類し、さらに遇置換は3次巡回置換、および3次巡回置換の積で表されることを確認していきます。すべて本シリーズ () からの抜粋です。
(注2)5次置換を遇置換と奇置換に分類(復習)
さて本シリーズ (15) で、5次置換すべてを互換の積で表し、遇置換と奇置換に分類しました。遇置換とは偶数個の互換の積で表せる置換であり、奇置換とは奇数個の互換の積で表せる置換です(本シリーズ (15))。
結果のみを再び確認します。
(case1) 動かない文字が5つの場合 $${1}$$ 通り 遇置換
例 恒等置換 $${I=(x_1 x_2)(x_1 x_2)}$$
(case2) 動かない文字が3つの場合 $${10}$$ 通り 奇置換
例 互換 $${(x_1 x_2)}$$
(case3) 動かない文字が2つの場合 $${20}$$ 通り 遇置換
例 3次巡回置換 $${(x_1 x_2 x_3)=(x_1 x_2)(x_1 x_3)}$$
これは共通の文字が1つある2つの互換の積とみることもできる。
(case4) 動かない文字が1つの場合
(case4-1) 共通の文字のない2つの互換の積 $${15}$$ 通り 遇置換
例 $${(x_1 x_2)(x_3 x_4)}$$
(case4-2) 4次巡回置換 $${30}$$ 通り 奇置換
例 $${(x_1 x_2 x_3 x_4)=(x_1 x_2)(x_1 x_3)(x_1 x_4)}$$
(case5) 動かない文字が0の場合
(case5-1) 互いに共通の文字のない、1つの互換と3次巡回置換との積 $${20}$$ 通り 奇置換
例 $${(x_1 x_2)(x_3 x_4 x_5)=(x_1 x_2)(x_3 x_4)(x_3 x_5)}$$
(case5-2) 5次巡回置換 $${24}$$ 通り
例 $${(x_1 x_2 x_3 x_4 x_5)=(x_1 x_2)(x_1 x_3)(x_1 x_4)(x_1 x_5)}$$ 遇置換
***
全部で何通りあるかを確認すると
(case1)+(case2)+(case3)+(case4-1)+(case4-2)+(case5-1)+(case5-2)
$${=1+10+20+15+30+20+24}$$
$${=120}$$ 通り
となります。そのうち遇置換は
(case1)+(case3)+(case4-1)+(case5-2)
$${=1+20+15+24}$$
$${=60}$$ 通り
奇置換は
(case2)+(case4-2)+(case5-1)
$${=10+30+20}$$
$${=60}$$ 通り
となり、遇置換と奇置換の数は、ちょうど半分ずつの $${60}$$ 通りになります。
(注3)60通りの遇置換を3次巡回置換で表す(復習)
任意の遇置換は3次巡回置換で表すことができます。
参考までに、先ほどの $${60}$$ 通りの遇置換について、それぞれのケースごとに3次巡回置換、および3次巡回置換の積で表していきます。本シリーズ (16) の復習です。3次巡回置換で表せることを列挙しているだけなので、読み飛ばしてもかまいません。
(case1) 動かない文字が5つの場合
この場合は何も変化させない恒等置換 $${I}$$ でした。3次巡回置換は同じ置換を3回繰り返せば元に戻るので、例えば
$$
\begin{align*}
I=(x_1 x_2 x_3)(x_1 x_2 x_3)(x_1 x_2 x_3)
\end{align*}
$$
と表すことによって、恒等置換を3次巡回置換の積で表すことができます。
(case3) 動かない文字が2つの場合
これは3次巡回置換そのもので、次のように $${①}$$ から $${⑮}$$ の $${15}$$ 通りの置換があります。
$$
\begin{align*}
&(x_1 〇 〇) 型\\
&① (x_1 x_2 x_3)\\
&② (x_1 x_2 x_4)\\
&③ (x_1 x_2 x_5)\\
&④ (x_1 x_3 x_2)\\
&⑤ (x_1 x_3 x_4)\\
&⑥ (x_1 x_3 x_5)\\
&⑦ (x_1 x_4 x_2)\\
&⑧ (x_1 x_4 x_3)\\
&⑨ (x_1 x_4 x_5)\\
&⑩ (x_1 x_5 x_2)\\
&⑪ (x_1 x_5 x_3)\\
&⑫ (x_1 x_5 x_4)\\[5pt]
&(x_2 〇 〇) 型\\
&⑬ (x_2 x_3 x_4)\\
&⑭ (x_2 x_3 x_5)\\
&⑮ (x_2 x_4 x_3)\\
&⑯ (x_2 x_4 x_5)\\
&⑰ (x_2 x_5 x_3)\\
&⑱ (x_2 x_5 x_4)\\[5pt]
&(x_3 〇 〇) 型\\
&⑲ (x_3 x_4 x_5)\\
&⑳ (x_3 x_5 x_4)
\end{align*}
$$
(case3) はすべて3次巡回置換です。
(case4) 動かない文字が1つの場合
(case4-1)
この場合は共通の文字のない2つの互換の積で、次のように $${①}$$ から $${⑮}$$ の $${15}$$ 通りの置換がありました。
(再掲)
$$
\begin{align*}
&(x_1 x_2)(〇 △) 型\\
&① (x_1 x_2)(x_3 x_4)\\
&② (x_1 x_2)(x_3 x_5)\\
&③ (x_1 x_2)(x_4 x_5)\\[5pt]
&(x_1 x_3)(〇 △) 型\\
&④ (x_1 x_3)(x_2 x_4)\\
&⑤ (x_1 x_3)(x_2 x_5)\\
&⑥ (x_1 x_3)(x_4 x_5)\\[5pt]
&(x_1 x_4)(〇 △) 型\\
&⑦ (x_1 x_4)(x_2 x_3)\\
&⑧ (x_1 x_4)(x_2 x_5)\\
&⑨ (x_1 x_4)(x_3 x_5)\\[5pt]
&(x_1 x_5)(〇 △) 型\\
&⑩ (x_1 x_5)(x_2 x_3)\\
&⑪ (x_1 x_5)(x_2 x_4)\\
&⑫ (x_1 x_5)(x_3 x_4)\\[5pt]
&(x_2 x_3)(〇 △) 型\\
&⑬ (x_2 x_3)(x_4 x_5)\\[5pt]
&(x_2 x_4)(〇 △) 型\\
&⑭ (x_2 x_4)(x_3 x_5)\\[5pt]
&(x_2 x_5)(〇 △) 型\\
&⑮ (x_2 x_5)(x_3 x_4)
\end{align*}
$$
なお、これらは共通の文字の無い互いに独立な互換の積なので、順番を入れ替えても同じものとなります。
(例)$${①}$$ について
$${(x_1 x_2)(x_3 x_4)=(x_3 x_4)(x_1 x_2)}$$
これらは、次の(公式2)

を用いれば、すべて3次巡回置換で表すことができます。例として $${①}$$ に関して具体的にやってみると
$$
\begin{align*}
(x_1 x_2)(x_3 x_4)&=(x_1 x_2)\underset{恒等置換を間に挟む}{\underline{(x_2 x_3)(x_2 x_3)}}(x_3 x_4)\\
&=\underset{前の2つをセット}{\underline{(x_1 x_2)(x_2 x_3)}}\,\underset{後ろの2つをセット}{\underline{\underline{(x_2 x_3)(x_3 x_4)}}}\\
&=\underset{先頭の文字をそろえる}{\underline{(x_2 x_1)(x_2 x_3)}}\,\underset{先頭の文字をそろえる}{\underline{\underline{(x_3 x_2)(x_3 x_4)}}}\\
&=\underset{公式1利用}{\underline{(x_2 x_1 x_3)}}\,\underset{公式1利用}{\underline{\underline{(x_3 x_2 x_4)}}}\\
&=\underset{並び替え}{\underline{(x_1 x_3 x_2)}}\,\underset{並び替え}{\underline{\underline{(x_2 x_4 x_3)}}}
\end{align*}
$$
と恒等置換をはさみ込む方法です。この変換を $${15}$$ 通りのすべての置換に実行すると、次のようになります。結果は先頭の文字の添え字の数が、最も小さくなるように整理しています。
$$
\begin{alignat*}{2}
&(x_1 x_2)(〇 △) 型\\
&① (x_1 x_2)(x_3 x_4) & &=(x_1 x_3 x_2)(x_2 x_4 x_3)\\
&② (x_1 x_2)(x_3 x_5) & &=(x_1 x_3 x_2)(x_2 x_5 x_3)\\
&③ (x_1 x_2)(x_4 x_5) & &=(x_1 x_4 x_2)(x_2 x_5 x_4)\\[5pt]
&(x_1 x_3)(〇 △) 型\\
&④ (x_1 x_3)(x_2 x_4) & &=(x_1 x_2 x_3)(x_3 x_4 x_2)\\
&⑤ (x_1 x_3)(x_2 x_5) & &=(x_1 x_2 x_3)(x_3 x_5 x_2)\\
&⑥ (x_1 x_3)(x_4 x_5) & &=(x_1 x_4 x_3)(x_3 x_5 x_4)\\[5pt]
&(x_1 x_4)(〇 △) 型\\
&⑦ (x_1 x_4)(x_2 x_3) & &=(x_1 x_2 x_4)(x_4 x_3 x_2)\\
& & &=(x_1 x_2 x_4)(x_2 x_4 x_3)\\
&⑧ (x_1 x_4)(x_2 x_5) & &=(x_1 x_2 x_4)(x_4 x_5 x_2)\\
& & &=(x_1 x_2 x_4)(x_2 x_4 x_5)\\
&⑨ (x_1 x_4)(x_3 x_5) & &=(x_1 x_3 x_4)(x_4 x_5 x_3)\\
& & &=(x_1 x_3 x_4)(x_3 x_4 x_5)\\[5pt]
&(x_1 x_5)(〇 △) 型\\
&⑩ (x_1 x_5)(x_2 x_3) & &=(x_1 x_2 x_5)(x_5 x_3 x_2)\\
& & &=(x_1 x_2 x_5)(x_2 x_5 x_3)\\
&⑪ (x_1 x_5)(x_2 x_4) & &=(x_1 x_2 x_5)(x_5 x_4 x_2)\\
& & &=(x_1 x_2 x_5)(x_2 x_5 x_4)\\
&⑫ (x_1 x_5)(x_3 x_4) & &=(x_1 x_3 x_5)(x_5 x_4 x_3)\\
& & &=(x_1 x_3 x_5)(x_3 x_5 x_4)\\[5pt]
&(x_2 x_3)(〇 △) 型\\
&⑬ (x_2 x_3)(x_4 x_5) & &=(x_2 x_4 x_3)(x_3 x_5 x_4)\\[5pt]
&(x_2 x_4)(〇 △) 型\\
&⑭ (x_2 x_4)(x_3 x_5) & &=(x_2 x_3 x_4)(x_4 x_5 x_3)\\
& & &=(x_2 x_3 x_5)(x_3 x_4 x_5)\\[5pt]
&(x_2 x_5)(〇 △) 型\\
&⑮ (x_2 x_5)(x_3 x_4) & &=(x_2 x_3 x_5)(x_5 x_4 x_3)\\
& & &=(x_2 x_3 x_5)(x_3 x_5 x_4)
\end{alignat*}
$$
これで (case4-1) のすべての互換の積を、3次巡回置換の積で表すことができました。
(case5) 動かない文字が0の場合
(case5-2)
この場合は5次巡回置換で、次のように $${①}$$ から $${㉔}$$ の $${24}$$ 通りの置換がありました。
(再掲)
$$
\begin{align*}
&(x_1 x_2 〇 △ \square) 型\\
&① (x_1 x_2 x_3 x_4 x_5)=(x_1 x_2)(x_1 x_3)(x_1 x_4)(x_1 x_5)\\
&② (x_1 x_2 x_3 x_5 x_4)=(x_1 x_2)(x_1 x_3)(x_1 x_5)(x_1 x_4)\\
&③ (x_1 x_2 x_4 x_3 x_5)=(x_1 x_2)(x_1 x_4)(x_1 x_3)(x_1 x_5)\\
&④ (x_1 x_2 x_4 x_5 x_3)=(x_1 x_2)(x_1 x_4)(x_1 x_5)(x_1 x_3)\\
&⑤ (x_1 x_2 x_5 x_3 x_4)=(x_1 x_2)(x_1 x_5)(x_1 x_3)(x_1 x_4)\\
&⑥ (x_1 x_2 x_5 x_4 x_3)=(x_1 x_2)(x_1 x_5)(x_1 x_4)(x_1 x_3)\\[5pt]
&(x_1 x_3 〇 △ \square) 型\\
&⑦ (x_1 x_3 x_2 x_4 x_5)=(x_1 x_3)(x_1 x_2)(x_1 x_4)(x_1 x_5)\\
&⑧ (x_1 x_3 x_2 x_5 x_4)=(x_1 x_3)(x_1 x_2)(x_1 x_5)(x_1 x_4)\\
&⑨ (x_1 x_3 x_4 x_2 x_5)=(x_1 x_3)(x_1 x_4)(x_1 x_2)(x_1 x_5)\\
&⑩ (x_1 x_3 x_4 x_5 x_2)=(x_1 x_3)(x_1 x_4)(x_1 x_5)(x_1 x_2)\\
&⑪ (x_1 x_3 x_5 x_2 x_4)=(x_1 x_3)(x_1 x_5)(x_1 x_2)(x_1 x_4)\\
&⑫ (x_1 x_3 x_5 x_4 x_2)=(x_1 x_3)(x_1 x_5)(x_1 x_4)(x_1 x_2)\\[5pt]
&(x_1 x_4 〇 △ \square) 型\\
&⑬ (x_1 x_4 x_2 x_3 x_5)=(x_1 x_4)(x_1 x_2)(x_1 x_3)(x_1 x_5)\\
&⑭ (x_1 x_4 x_2 x_5 x_3)=(x_1 x_4)(x_1 x_2)(x_1 x_5)(x_1 x_3)\\
&⑮ (x_1 x_4 x_3 x_2 x_5)=(x_1 x_4)(x_1 x_3)(x_1 x_2)(x_1 x_5)\\
&⑯ (x_1 x_4 x_3 x_5 x_2)=(x_1 x_4)(x_1 x_3)(x_1 x_5)(x_1 x_2)\\
&⑰ (x_1 x_4 x_5 x_2 x_3)=(x_1 x_4)(x_1 x_5)(x_1 x_2)(x_1 x_3)\\
&⑱ (x_1 x_4 x_5 x_3 x_2)=(x_1 x_4)(x_1 x_5)(x_1 x_3)(x_1 x_2)\\[5pt]
&(x_1 x_5 〇 △ \square) 型\\
&⑲ (x_1 x_5 x_2 x_3 x_4)=(x_1 x_5)(x_1 x_2)(x_1 x_3)(x_1 x_4)\\
&⑳ (x_1 x_5 x_2 x_4 x_3)=(x_1 x_5)(x_1 x_2)(x_1 x_4)(x_1 x_3)\\
&㉑ (x_1 x_5 x_3 x_2 x_4)=(x_1 x_5)(x_1 x_3)(x_1 x_2)(x_1 x_4)\\
&㉒ (x_1 x_5 x_3 x_4 x_2)=(x_1 x_5)(x_1 x_3)(x_1 x_4)(x_1 x_2)\\
&㉓ (x_1 x_5 x_4 x_2 x_3)=(x_1 x_5)(x_1 x_4)(x_1 x_2)(x_1 x_3)\\
&㉔ (x_1 x_5 x_4 x_3 x_2)=(x_1 x_5)(x_1 x_4)(x_1 x_3)(x_1 x_2)
\end{align*}
$$
これらは前2つと後ろ2つに分けで、それぞれは共通の文字のある互換の積なので、(公式1)

を用いて3次巡回置換に変換します。例えば $${①}$$ について具体的にやってみると
$$
\begin{align*}
(x_1 x_2 x_3 x_4 x_5)&=\,\underset{前の2つをセット}{\underline{(x_1 x_2)(x_1 x_3)}}\,\underset{後ろの2つをセット}{\underline{\underline{(x_1 x_4)(x_1 x_5)}}}\\
&=\,\underset{公式1を利用}{\underline{(x_1 x_2 x_3)}}\,\underset{公式1を利用}{\underline{\underline{(x_1 x_4 x_5)}}}
\end{align*}
$$
この変形をすべての置換に実行していくと、次のようになります。
$$
\begin{alignat*}{2}
&(x_1 x_2 〇 △ \square) 型\\
&① (x_1 x_2 x_3 x_4 x_5) & &=(x_1 x_2)(x_1 x_3)(x_1 x_4)(x_1 x_5)\\
& & &=(x_1 x_2 x_3)(x_1 x_4 x_5)\\
&② (x_1 x_2 x_3 x_5 x_4) & &=(x_1 x_2)(x_1 x_3)(x_1 x_5)(x_1 x_4)\\
& & &=(x_1 x_2 x_3)(x_1 x_5 x_4)\\
&③ (x_1 x_2 x_4 x_3 x_5) & &=(x_1 x_2)(x_1 x_4)(x_1 x_3)(x_1 x_5)\\
& & &=(x_1 x_2 x_4)(x_1 x_3 x_5)\\
&④ (x_1 x_2 x_4 x_5 x_3) & &=(x_1 x_2)(x_1 x_4)(x_1 x_5)(x_1 x_3)\\
& & &=(x_1 x_2 x_4)(x_1 x_5 x_3)\\
&⑤ (x_1 x_2 x_5 x_3 x_4) & &=(x_1 x_2)(x_1 x_5)(x_1 x_3)(x_1 x_4)\\
& & &=(x_1 x_2 x_5)(x_1 x_3 x_4)\\
&⑥ (x_1 x_2 x_5 x_4 x_3) & &=(x_1 x_2)(x_1 x_5)(x_1 x_4)(x_1 x_3)\\
& & &=(x_1 x_2 x_5)(x_1 x_4 x_3)\\[5pt]
&(x_1 x_3 〇 △ \square) 型\\
&⑦ (x_1 x_3 x_2 x_4 x_5) & &=(x_1 x_3)(x_1 x_2)(x_1 x_4)(x_1 x_5)\\
& & &=(x_1 x_3 x_2)(x_1 x_4 x_5)\\
&⑧ (x_1 x_3 x_2 x_5 x_4) & &=(x_1 x_3)(x_1 x_2)(x_1 x_5)(x_1 x_4)\\
& & &=(x_1 x_3 x_2)(x_1 x_5 x_4)\\
&⑨ (x_1 x_3 x_4 x_2 x_5) & &=(x_1 x_3)(x_1 x_4)(x_1 x_2)(x_1 x_5)\\
& & &=(x_1 x_3 x_4)(x_1 x_2 x_5)\\
&⑩ (x_1 x_3 x_4 x_5 x_2) & &=(x_1 x_3)(x_1 x_4)(x_1 x_5)(x_1 x_2)\\
& & &=(x_1 x_3 x_4)(x_1 x_5 x_2)\\
&⑪ (x_1 x_3 x_5 x_2 x_4) & &=(x_1 x_3)(x_1 x_5)(x_1 x_2)(x_1 x_4)\\
& & &=(x_1 x_3 x_5)(x_1 x_2 x_4)\\
&⑫ (x_1 x_3 x_5 x_4 x_2) & &=(x_1 x_3)(x_1 x_5)(x_1 x_4)(x_1 x_2)\\
& & &=(x_1 x_3 x_5)(x_1 x_4 x_2)\\[5pt]
&(x_1 x_4 〇 △ \square) 型\\
&⑬ (x_1 x_4 x_2 x_3 x_5) & &=(x_1 x_4)(x_1 x_2)(x_1 x_3)(x_1 x_5)\\
& & &=(x_1 x_4 x_2)(x_1 x_3 x_5)\\
&⑭ (x_1 x_4 x_2 x_5 x_3) & &=(x_1 x_4)(x_1 x_2)(x_1 x_5)(x_1 x_3)\\
& & &=(x_1 x_4 x_2)(x_1 x_5 x_3)\\
&⑮ (x_1 x_4 x_3 x_2 x_5) & &=(x_1 x_4)(x_1 x_3)(x_1 x_2)(x_1 x_5)\\
& & &=(x_1 x_4 x_3)(x_1 x_2 x_5)\\
&⑯ (x_1 x_4 x_3 x_5 x_2) & &=(x_1 x_4)(x_1 x_3)(x_1 x_5)(x_1 x_2)\\
& & &=(x_1 x_4 x_3)(x_1 x_5 x_2)\\
&⑰ (x_1 x_4 x_5 x_2 x_3) & &=(x_1 x_4)(x_1 x_5)(x_1 x_2)(x_1 x_3)\\
& & &=(x_1 x_4 x_5)(x_1 x_2 x_3)\\
&⑱ (x_1 x_4 x_5 x_3 x_2) & &=(x_1 x_4)(x_1 x_5)(x_1 x_3)(x_1 x_2)\\
& & &=(x_1 x_4 x_5)(x_1 x_3 x_2)\\[5pt]
&(x_1 x_5 〇 △ \square) 型\\
&⑲ (x_1 x_5 x_2 x_3 x_4) & &=(x_1 x_5)(x_1 x_2)(x_1 x_3)(x_1 x_4)\\
& & &=(x_1 x_5 x_2)(x_1 x_3 x_4)\\
&⑳ (x_1 x_5 x_2 x_4 x_3) & &=(x_1 x_5)(x_1 x_2)(x_1 x_4)(x_1 x_3)\\
& & &=(x_1 x_5 x_2)(x_1 x_4 x_3)\\
&㉑ (x_1 x_5 x_3 x_2 x_4) & &=(x_1 x_5)(x_1 x_3)(x_1 x_2)(x_1 x_4)\\
& & &=(x_1 x_5 x_3)(x_1 x_2 x_4)\\
&㉒ (x_1 x_5 x_3 x_4 x_2) & &=(x_1 x_5)(x_1 x_3)(x_1 x_4)(x_1 x_2)\\
& & &=(x_1 x_5 x_3)(x_1 x_4 x_2)\\
&㉓ (x_1 x_5 x_4 x_2 x_3) & &=(x_1 x_5)(x_1 x_4)(x_1 x_2)(x_1 x_3)\\
& & &=(x_1 x_5 x_4)(x_1 x_2 x_3)\\
&㉔ (x_1 x_5 x_4 x_3 x_2) & &=(x_1 x_5)(x_1 x_4)(x_1 x_3)(x_1 x_2)\\
& & &=(x_1 x_5 x_4)(x_1 x_3 x_2)\\
\end{alignat*}
$$
これで (case5) のすべての5次巡回置換を、3次巡回置換の積で表すことができました。
以上で60通りすべての遇置換を3次巡回置換、または3次巡回置換の積で表せたことになります。結果をまとめておきます。
まとめ
(case1) 動かない文字が5つの場合 $${1}$$ 通り
例 恒等置換 $${I=(x_1 x_2 x_3)(x_1 x_2 x_3)(x_1 x_2 x_3)}$$
これは3次巡回置換の3つの積です。
(case3) 動かない文字が2つの場合 $${20}$$ 通り
例 3次巡回置換 $${(x_1 x_2 x_3)}$$
これは1つの3次巡回置換です。
(case4) 動かない文字が1つの場合
(case4-1) 共通の文字のない2つの互換の積 $${15}$$ 通り
例 $${(x_1 x_2)(x_3 x_4)=(x_1 x_3 x_2)(x_2 x_4 x_3)}$$
これは3次巡回置換の2つの積です。
(case5) 動かない文字が0の場合
(case5-2) 5次巡回置換 $${24}$$ 通り
例 $${(x_1 x_2 x_3 x_4 x_5)=(x_1 x_2 x_3)(x_1 x_4 x_5)}$$
これは3次巡回置換の2つの積です。
(参考)各章の内容
(1)「2次方程式の解の公式」を式変形で導出
・平方完成
(2)「3次方程式の解の公式」を導出するための準備
・$${1}$$ の3乗根 $${\omega}$$
(3)「3次方程式の解の公式」を式変形で導出
・チルンハウス変換
(4)「解と係数の関係」と「対称式」の解説
(5)「対称式」を用いた「2次方程式の解の公式」の導出
(6)「解の置換」と「ラグランジュ・リゾルベント」の解説
(7)「ラグランジュ・リゾルベントの連立」による「3次方程式の解の公式」の導出
(8)「遇置換」と「奇置換」の解説(ここから「アーベルの証明」の準備)
(9)「差積の2乗」が対称式となること、及び「差積」と平方根を結ぶ等式の証明。
(10)「平方根」「3乗根」と次々と累乗根を加えていくアイデア
(11)「アーベルの証明」のアイデアを用いて、なぜ「2次方程式の解の公式が存在するのか」を解説(添加する式について加筆予定)
(12)「アーベルの証明」のアイデアを用いて、なぜ「3次方程式の解の公式が存在するのか」を解説(前編)。「差積の2乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む(対称性の破壊)。
(13)「アーベルの証明」のアイデアを用いて、なぜ「3次方程式の解の公式が存在するのか」を解説(後編)。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む(対称性の破壊)。$${\longrightarrow}$$ 3次方程式の解の公式の完成
(14)「アーベルの証明」の解説①。5次方程式の解の差積(または差積の2乗の平方根)を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が5次置換(対称式)から遇置換シンメトリーへと破壊されることを解説。
(15)「アーベルの証明」の解説②。すべての置換は互換で表せることから、5次置換をすべて互換の積で表して、遇置換と奇置換に分類する。
(16)「アーベルの証明」の解説➂。「すべての遇置換は3次巡回置換の積で表される」ことの解説。
(17)「アーベルの証明」の解説➃(最後)。「任意の3次巡回置換が5次巡回置換の積で表せる」ことによって、5次方程式には解の公式が存在しないことが証明されることの解説。
(18)もっと分かりやすくシリーズ①「累乗根の添加」について重点解説。
(19)もっと分かりやすくシリーズ②「対称性の破壊」について重点解説。
(20)もっと分かりやすくシリーズ③「対称性を恒等置換まで破壊」することについて重点解説。
(21)もっと分かりやすくシリーズ➃ 何次方程式でも「最初に解の差積を添加して対称性を破壊すること」は常套手段。
(22)もっと分かりやすくシリーズ➄「解の和と差の連立」による2次方程式の解の公式の導出について。
(23)もっと分かりやすくシリーズ➅「対称式ではない解の公式を基本対称式で表す」ことのついて。
(24)もっと分かりやすくシリーズ➆「定数 $${\bm{\omega}}$$」について復習
(25)もっと分かりやすくシリーズ➇ 3次方程式の解の公式の導出方法「カルダノの方法」を復習
(26)もっと分かりやすくシリーズ➈「カルダノの方法」と「対称性の破壊」の関連について
(27)もっと分かりやすくシリーズ⑩ そもそもなぜ解の公式が存在しないかを『巡回置換』から紐解く
(28)中学でも分かるガロアの証明① ガロアの発見した「群」について簡単に解説
(29)中学でも分かるガロアの証明➁ ガロアの発見した「部分群」について簡単に解説
(30)中学でも分かるガロアの証明③ ガロアの発見した「正規部分群」について
(31)中学でも分かるガロアの証明➃ 正規部分群による剰余類の集合が群(剰余群)になること
(32)中学でも分かるガロアの証明⑤ 単位元のみの正規部分群 $${\{𝑖𝑑\}}$$ による剰余類の集合が群(剰余群)になること
(33)中学でも分かるガロアの証明⑥ 「巡回群」について、および剰余群が巡回群になること
(34)中学でも分かるガロアの証明⑦ 2次対称群で、正規部分群による剰余群が巡回群になることの復習
(35)中学でも分かるガロアの証明⑧ 「体」について解説
(36)中学でも分かるガロアの証明➈ 2次方程式に解の公式が存在することを、2次対称群が「可解群」になることによって証明する
(36)中学でも分かるガロアの証明➈ 3次方程式に解の公式が存在することを、3次対称群が「可解群」になることによって証明する
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
