２次方程式に解の公式が存在することを「群」で証明する

連立による２次方程式の解の公式の導出

　２次方程式 $${ax^2+bx+c=0}$$ の解を $${\alpha,  \beta}$$ とします。
　２次方程式の解の公式の導出方法には、本シリーズ (1) でやった、中学で習う「平方完成」と、もう一つ、$${\alpha+\beta}$$ と $${\alpha-\beta}$$ による連立方程式

$$
\begin{cases}
\alpha+\beta=\bigcirc\\
\alpha-\beta=\square
\end{cases}
$$

を解くことを、本シリーズ (22) でやりました。
　解の公式とは、解 $${x}$$ を係数 $${a,  b,  c}$$ を用いて表すことです。
　この $${\bigcirc}$$ と $${\square}$$ を２次方程式の係数 $${a,  b,  c}$$ で表すことができれば、後はこの２式の連立方程式を解くこと、つまり $${\alpha+\beta=\bigcirc}$$ と $${\alpha-\beta=\square}$$ の加減乗除のみによって $${\alpha,  \beta}$$ を求めることができ、それが解の公式

$$
\begin{align*}
x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{align*}
$$

となります。
　第１式 $${\alpha+\beta=\bigcirc}$$ の方は、＜解と係数の関係＞の最初の式から容易に分かります（本シリーズ (4)）。

＜解と係数の関係＞（復習）

　２次方程式 $${ax^2+bx+c=0}$$ の解 $${\alpha,  \beta}$$ について

$$
\begin{align*}
\alpha+\beta&=-\dfrac{b}{a}\\
\alpha\beta&=\dfrac{c}{a}
\end{align*}
$$

＊＊＊

　つまり

$$
\begin{cases}
\alpha+\beta=-\dfrac{b}{a}\\
\alpha-\beta=\square
\end{cases}
$$

と、第１式が決定します。
　では、第２式 $${\alpha-\beta}$$ はどのように求めるでしょうか。それには差積の２乗

$$
\begin{align*}
(\alpha-\beta)^2
\end{align*}
$$

を考えます。
　ここで、文字を入れ替えても変化しない式を対称式といいました（本シリーズ (4)）。
　例えば、次のような式は $${\alpha}$$ と $${\beta}$$ を入れ換えても変化しないので（２変数の）対称式です。特に、上の２つを基本対称式といいます。

　$${\alpha+\beta}$$（基本対称式）
　$${\alpha\beta}$$（基本対称式）
　$${\alpha^2+\beta^2}$$
　$${(\alpha-\beta)^2　\cdots (*1)}$$

　しかし、次のような式は $${\alpha}$$ と $${\beta}$$ を入れ換えると変化するので対称式ではありません。

　$${\alpha-\beta　\cdots (*2)}$$
　$${\alpha^2-\beta^2}$$
　$${\dfrac{\beta}{\alpha}}$$

　ここで重要なのは、上式 $${(*1)}$$ と $${(*2)}$$ の関係です。
　$${\alpha-\beta}$$ は、$${\alpha}$$ と $${\beta}$$ の入れ換えで変化するので対称式ではありませんが、$${(\alpha-\beta)^2}$$ は変化しないので対称式です。

$$
\begin{align*}
\\
\alpha-\beta  &\xrightarrow[入れ替えると]{\alpha  と  \beta  を}  \beta-\alpha=-(\alpha-\beta)\\[8pt]
&\xrightarrow[\hspace{42pt}]{}  {\small 変化するので対称式ではない}\\[8pt]
(\alpha-\beta)^2  &\xrightarrow[入れ替えると]{\alpha  と  \beta  を}  (\beta-\alpha)^2=(\alpha-\beta)^2\\[8pt]
&\xrightarrow[\hspace{42pt}]{}  {\small 変化しないので対称式である}
\end{align*}
$$

　$${\alpha-\beta}$$ を求めるには、このことを利用します（本シリーズ (22)）。すると、

＜対称式の基本定理＞（復習）

　「すべての対称式は、基本対称式 $${\alpha+\beta,  \alpha\beta}$$ の加減乗除で表すことができる」

＊＊＊

より、対称式である $${(\alpha-\beta)^2}$$ は、基本対称式の加減乗除で表すことが可能です。実際に計算すると

$$
\begin{align*}
{(\alpha-\beta)}^2&=\alpha^2-2\alpha\beta+\beta^2  {\small（因数分解）}\\
&=\underline{\alpha^2+\beta^2}-2\alpha\beta\\
&=\underline{{(\alpha+\beta)}^2-2\alpha\beta}-2\alpha\beta\\
&={(\hspace{-5pt}\underbrace{\alpha+\beta}_{基本対称式}\hspace{-5pt})}^2-4\hspace{-11pt}\underbrace{\alpha\beta}_{基本対称式}
\end{align*}
$$

　これで、対称式 $${(\alpha+\beta)^2}$$ を基本対称式の加減乗除で表すことができました。
　下線部は中学３年で習う次の因数分解公式
　$${\alpha^2+2\alpha\beta+\beta^2=(\alpha+\beta)^2}$$
について、$${2\alpha\beta}$$ を移項して
　$${\alpha^2+\beta^2=(\alpha+\beta)^2-s\alpha\beta}$$
とすれば得られます。
　ここで、先ほどやった

＜解と係数の関係＞

　２次方程式 $${ax^2+bx+c=0}$$ の解 $${\alpha,  \beta}$$ について

$$
\begin{align*}
\alpha+\beta&=-\dfrac{b}{a}\\
\alpha\beta&=\dfrac{c}{a}
\end{align*}
$$

＊＊＊

を基本対称式の部分に代入して

$$
\begin{align*}
{(\alpha-\beta)}^2&={(\hspace{-5pt}\underbrace{\alpha+\beta}_{基本対称式}\hspace{-5pt})}^2-4\hspace{-11pt}\underbrace{\alpha\beta}_{基本対称式}\\
&={\left(-\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}\\
&={\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}
\end{align*}
$$

より

$$
\begin{align*}
{(\alpha-\beta)}^2={\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}
\end{align*}
$$

　さらに、「$${x^2=3}$$ を解くと $${x=\pm\sqrt{3}}$$」と同じ形式の計算より

$$
\begin{align*}
{(\alpha-\beta)}^2&={\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}\\[10pt]
&\,\downarrow  {\footnotesize ２乗をはずすとプラスマイナスルート}\\[2pt]
\alpha-\beta&=\pm\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}
\end{align*}
$$

　これで $${\alpha-\beta}$$ を係数 $${a,  b,  c}$$ を用いて表すことができました。「平方根（ルート）を取る」という操作がここで出てきます。加減乗除では表せない「平方根を取る」という新しい操作です。
　これで、連立方程式の第２式  $${\square}$$ が決定したので、次の連立方程式

$$
\begin{cases}
\alpha+\beta=-\dfrac{b}{a}\\[10pt]
\alpha-\beta=\pm\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}
\end{cases}
$$

を解くことにより、$${\alpha,  \beta}$$ を求めることができます。

連立方程式を解く

　計算は本シリーズ (22) でもやりましたが、少しだけ方法を変えて、ここでも計算します。分かりきっている場合は飛ばしてもかまいません。
　簡単のため
(case1)　$${\alpha-\beta=\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}$$  のとき
(case2)　$${\alpha-\beta=-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}$$  のとき
で場合分けをします。

(case1)　$${\alpha-\beta=\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}$$  のとき
　辺々足して $${\beta}$$ を消去して

$$
\begin{alignat*}{2}
&\alpha+\cancel{\beta}& &=-\dfrac{b}{a}\\[8pt]
+\,)   &\alpha-\cancel{\beta}& &=\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}\\[-10pt]
&\hspace{-8pt}\underline{\hspace{34pt}} & &\underline{\hspace{100pt}}\\
2&\alpha& &=-\dfrac{b}{a}+\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}\\[8pt]
&\alpha& &=\dfrac{-\dfrac{b}{a}+\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{alignat*}
$$

　辺々引いて $${\alpha}$$ を消去して

$$
\begin{alignat*}{2}
&\cancel{\alpha}+\beta& &=-\dfrac{b}{a}\\[8pt]
-\,)   &\cancel{\alpha}-\beta& &=\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}\\[-10pt]
&\hspace{-8pt}\underline{\hspace{34pt}} & &\underline{\hspace{100pt}}\\
&\hspace{14pt}2\beta & &=-\dfrac{b}{a}-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}\\[8pt]
&\hspace{18pt}\beta & &=\dfrac{-\dfrac{b}{a}-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{alignat*}
$$

　よって

$$
\begin{cases}
\alpha=\dfrac{-\dfrac{b}{a}+\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}\\[8pt]
\beta=\dfrac{-\dfrac{b}{a}-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{cases}
$$

(case2)　$${\alpha-\beta=-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}$$  のとき
　辺々足して $${\beta}$$ を消去して

$$
\begin{alignat*}{2}
&\alpha+\cancel{\beta}& &=-\dfrac{b}{a}\\[8pt]
+\,)   &\alpha-\cancel{\beta}& &=-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}\\[-10pt]
&\hspace{-8pt}\underline{\hspace{34pt}} & &\underline{\hspace{100pt}}\\
2&\alpha& &=-\dfrac{b}{a}-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}\\[8pt]
&\alpha& &=\dfrac{-\dfrac{b}{a}-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{alignat*}
$$

　辺々引いて $${\alpha}$$ を消去して

$$
\begin{alignat*}{2}
&\cancel{\alpha}+\beta& &=-\dfrac{b}{a}\\[8pt]
-\,)   &\cancel{\alpha}-\beta& &=-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}\\[-10pt]
&\hspace{-8pt}\underline{\hspace{34pt}} & &\underline{\hspace{100pt}}\\
&\hspace{14pt}2\beta & &=-\dfrac{b}{a}+\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}\\[8pt]
&\hspace{18pt}\beta & &=\dfrac{-\dfrac{b}{a}+\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{alignat*}
$$

　よって

$$
\begin{cases}
\alpha=\dfrac{-\dfrac{b}{a}-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}\\[8pt]
\beta=\dfrac{-\dfrac{b}{a}+\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{cases}
$$

　以上により

(case1) のとき

$$
\begin{cases}
\alpha=\dfrac{-\dfrac{b}{a}+\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}\\[8pt]
\beta=\dfrac{-\dfrac{b}{a}-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{cases}
$$

(case2) のとき

$$
\begin{cases}
\alpha=\dfrac{-\dfrac{b}{a}-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}\\[8pt]
\beta=\dfrac{-\dfrac{b}{a}+\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{cases}
$$

となりますが、(case1) と (case2) はプラスとマイナスを入れ換えただけです。$${\alpha}$$ と $${\beta}$$ は２次方程式 $${ax^2+bx+c=0}$$ の解 $${x}$$ なので、$${\alpha,  \beta}$$ を $${x}$$ にして

$$
\begin{cases}
x=\dfrac{-\dfrac{b}{a}+\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}\\[8pt]
x=\dfrac{-\dfrac{b}{a}-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{cases}
$$

　これを、プラスマイナスで一つにまとめて

$$
\begin{align*}
x=\dfrac{-\dfrac{b}{a}\pm\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{align*}
$$

　これで、２次方程式の解の公式が得られたことになります。さらに、以下のように計算していくと 、教科書で馴染みのある形での解の公式が得られます。

$$
\begin{align*}
x&=\dfrac{-\dfrac{b}{a}\pm\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}\\[8pt]
&=\dfrac{-\dfrac{b}{a}\pm\sqrt{\dfrac{b^2}{a^2}-4\cdot\dfrac{c}{a}}}{2}\\[8pt]
&=\dfrac{-\dfrac{b}{a}\pm\sqrt{\dfrac{b^2}{a^2}-4\cdot\dfrac{ac}{a^2}}}{2}\\[8pt]
&=\dfrac{-\dfrac{b}{a}\pm\sqrt{\dfrac{b^2}{a^2}-\dfrac{4ac}{a^2}}}{2}\\[8pt]
&=\dfrac{-\dfrac{b}{a}\pm\sqrt{\dfrac{b^2-4ac}{a^2}}}{2}\\[8pt]
&=\dfrac{-\dfrac{b}{a}\pm\dfrac{\sqrt{b^2-4ac}}{a}}{2}\\[8pt]
&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{align*}
$$

 より

$$
\begin{align*}
x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{align*}
$$

　つまり、解の公式を得るためには
　$${\alpha+\beta}$$  と  $${\alpha-\beta}$$
を２次方程式の係数 $${a,  b,  c}$$ を用いて決定し、それらを連立すればよいということです。
　なお、本シリーズ (22) では、次のような解に関する恒等式（常に成り立つ等式）を用いました。

$$
\begin{align*}
\alpha&=\dfrac{(\alpha+\beta)+(\alpha-\beta)}{2}\\
\beta&=\dfrac{(\alpha+\beta)-(\alpha-\beta)}{2}\\
\end{align*}
$$

　$${①}$$ と $${②}$$ を足して $${2}$$ で割ったのが $${\alpha}$$、$${①}$$ から $${②}$$ を引いて $${2}$$ で割ったのが $${\beta}$$ という意味です。

$$
\begin{align*}
\\[12pt]
\alpha&=\dfrac{①+②}{2}\\
\beta&=\dfrac{①-②}{2}
\end{align*}
$$

　証明は、右辺を計算すれば左辺になることで簡単に証明できます（本シリーズ (22)）。

解の公式の導出を「体の拡大」と関連付ける

　ここで、ここまでの流れを、本シリーズ (35) でやった「体の拡大」と関連付けましょう。

差積の添加による体の拡大

　２次方程式 $${ax^2+bx+c=0}$$ の係数 $${a,  b,  c}$$ と有理数の加減乗除で閉じている体を $${Q_2}$$ とします。拡大する前の最初の体なので基礎体となります（本シリーズ(35)）。係数による体なので、係数体と記しているテキストもあります。

　$${Q_2=\hspace{-4pt}}$$｛係数 $${a,  b,  c}$$ と有理数の加減乗除で閉じている体｝

　この $${Q_2}$$ は、２変数の対称式の集合となることは、本シリーズ (19) でやりました。この集合の要素は２変数 $${\alpha,  \beta}$$ の対称式（および有理数）で、かつ任意の２変数 $${\alpha,  \beta}$$ の対称式を取ってくれば、その対称式はすべてこの $${Q_2}$$ の中に含まれます。

　ここで、２次方程式 $${ax^2+bx+c=0}$$ の解を $${\alpha,  \beta}$$ とすると、その解の差積 $${X_2}$$ は次のようなものです。

$$
\begin{align*}
X_2=\alpha-\beta
\end{align*}
$$

　先に出てきた
　$${(X_2)^2=(\alpha-\beta)^2}$$
は対称式なので、$${Q_2}$$ 内で構成可能、つまり、係数 $${a,  b,  c}$$ と有理数の加減乗除でつくることが可能です。実際計算すると、次のようになることは先にやりました。

$$
\begin{align*}
(X_2)^2={(\alpha-\beta)}^2={\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}
\end{align*}
$$

　しかし、$${X_2=\alpha-\beta}$$ そのものは対称式ではないので、$${Q_2}$$ 内で構成可能ではありません。

　そこで、この差積 $${X_2}$$ を $${Q_2}$$ に添加し、その拡大された体（拡大体）を $${Q_2(X_2)}$$ とします。

　$${Q_2(X_2)=\hspace{-4pt}}$$｛係数 $${a,  b,  c}$$ と差積 $${X_2}$$ と有理数の加減乗除で閉じている体｝

　先の計算により、$${X_2=\alpha-\beta}$$ は次のように平方根で表されます。

$$
\begin{align*}
X_2=\alpha-\beta=\pm\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}
\end{align*}
$$

　つまり $${X_2}$$ の添加は、解の公式に必要な「平方根」の添加となります。
　すると、$${\alpha-\beta}$$ の添加された拡大体 $${Q_2(X_2)}$$ 内では、先にやったように連立方程式

$$
\begin{cases}
\alpha+\beta=-\dfrac{b}{a}\\[10pt]
\alpha-\beta=\pm\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}
\end{cases}
$$

を、（足したり引いたりの加減乗除で）解くことが可能となるので、 $${Q_2(X_2)}$$ 内で２次方程式の解の公式を構成（導出）することができます（本シリーズ (21)）。

　基礎体 $${Q_2}$$ 内では２次方程式の解の公式は構成できませんが、拡大体 $${Q_2(X_2)}$$ 内では構成できるようになるのです。
　この「体の拡大」のアイデアは、（体という言葉こそ用いてはいませんが）アーベルの証明でもあらわれます（本シリーズのアーベルの証明）。しかし、このアイデアを群構造と結びつけることによって、より厳密な理論として提出したのがガロアです。
　これについて残りの章で解説していきますが、そのためにはいろいろな準備が必要なので１つずつ攻略していきます。

差積と巡回群の同一構造

　ここで２次置換を考えます。２次置換には次の２種類があります（本シリーズ (6)）。

$$
\begin{align*}
&➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta\\
\alpha & \beta
\end{pmatrix}
=id\\
\\
&➁\hspace{6pt}
\begin{pmatrix}
\alpha & \beta\\
\beta & \alpha
\end{pmatrix}
=(\alpha     \beta)
=\tau\\
\end{align*}
$$

　$${➀}$$ は $${\alpha}$$ を $${\alpha}$$ に、$${\beta}$$ を $${\beta}$$ に置き換える、つまり何も変化しない恒等置換です。これを $${id}$$ とおきます。
　$${➁}$$ は $${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に入れ換える置換です。これを互いに交換するという意味で互換といいます。これを $${\tau}$$ とおきます。

　すると、$${X_2}$$ に $${\tau}$$ を作用させると $${-X_2}$$（$${-1}$$ 倍）に変化し、もう一度 $${\tau}$$ を作用させると、さらに $${-1}$$ 倍で元に戻ります。
　つまり、差積 $${X_2}$$ と $${-X_2}$$ は、$${\tau}$$ という演算に関して巡回しています。

$$
\begin{align*}
X_2&=\alpha-\beta\\
&\,\downarrow  {\small \tau  を作用（-1  倍）}\\
-X_2&=-(\alpha-\beta)\\
&\,\downarrow  {\small \tau  を作用（-1  倍）}\\
X_2&=\alpha-\beta\\
&\,\downarrow  {\small \tau  を作用（-1  倍）}\\
-X_2&=-(\alpha-\beta)\\
&\,\downarrow  {\small \tau  を作用（-1  倍）}\\
&\hspace{6pt}\vdots　{\small  巡回的に繰り返される}
\end{align*}
$$

　また、$${X_2}$$ と $${-X_2}$$ に $${id}$$ を作用させても変化しません。

$$
\begin{align*}
&\begin{align*}
X_2&=\alpha-\beta\\
&\,\downarrow  {\small id  を作用}\\
X_2&=\alpha-\beta {\small（変化しない）}
\end{align*}
\hspace{0pt}
&\begin{align*}
-X_2&=-(\alpha-\beta)\\
&\,\downarrow  {\small id  を作用}\\
-X_2&=-(\alpha-\beta) {\small（変化しない）}
\end{align*}
\end{align*}
$$

　図示すると次のように表せます。

　これと、本シリーズ (34) でやった $${S_2}$$ の正規部分群
　$${I=\{id\}}$$
による左剰余類の集合（剰余群）
　$${\{idI,  \tau I\}}$$
が巡回群になることと比較してみましょう。
　この巡回群 $${\{idI,  \tau I\}}$$ の要素について、その積の演算表（群表）は次のようなものでした。

$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & idI & \utilde{\underline{\tau I}}\\ \hline\hline
\underline{idI} & idI & \underline{\tau I}\\ \hline
\utilde{\tau I} & \tau I & \utilde{idI}
\end{array}
$$

　これより
　$${id I \circ \tau I=\tau I}$$（下線部）
　$${\tau I \circ \tau I=id I}$$（波線部）
なので、$${id I}$$ に $${\tau I}$$ を作用させると $${\tau I}$$ に変化し、もう一度 $${\tau I}$$ を作用させると元に戻ります。
　つまり、巡回群 $${\{idI,  \tau I\}}$$ の要素は、$${\tau I}$$ との積に関して巡回しています。

$$
\begin{align*}
&idI\\
&\,\downarrow  {\small \tau I  を作用}\\
&\tau I\\
&\,\downarrow  {\small \tau I  を作用}\\
&id I\\
&\,\downarrow  {\small \tau I  を作用}\\
&\tau I\\
&\,\downarrow  {\small \tau I  を作用}\\
&\hspace{6pt}\vdots　{\small  巡回的に繰り返される}
\end{align*}
$$

　また

$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & \utilde{\underline{idI}} & \tau I\\ \hline\hline
\underline{idI} & \underline{idI} & \tau I\\ \hline
\utilde{\tau I} & \utilde{\tau I} & idI
\end{array}
$$

より
　$${id I \circ id I=id I}$$（下線部）
　$${\tau I \circ id I=\tau I}$$（波線部）
なので、$${idI}$$ と $${\tau I}$$ に $${idI}$$ を作用させても変化しません。群のことばでいうと $${idI}$$ は単位元です。

$$
\begin{align*}
&\begin{align*}
&id I\\
&\,\downarrow  {\small id I  を作用}\\
&id I {\small（変化しない）}
\end{align*}
\hspace{10pt}
&\begin{align*}
&\tau I\\
&\,\downarrow  {\small id I  を作用}\\
&\tau I {\small（変化しない）}
\end{align*}
\end{align*}
$$

　図示すると次のように表せます。

 すると、２次方程式の解の差積
　$${X_2=\alpha-\beta}$$
と巡回群
　$${\{idI,  \tau I\}}$$
には、下図のように、巡回構造をもつ同じ構造がみられます。

＜$${\bm{\alpha-\beta}}$$ について＞

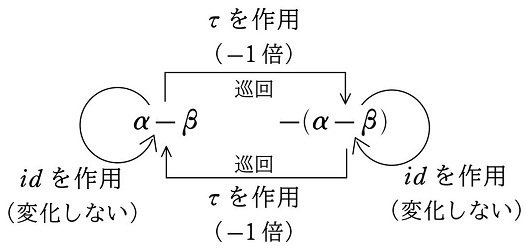
$${\hspace{40pt}\updownarrow}$$  同じ構造

＜$${\bm{\{idI,  \tau I\}}}$$ について＞

　数学は、同じ構造のものを同一視して考えることがよくあります。
　つまり、「差積 $${X_2}$$ が置換 $${\tau}$$ に関して巡回すること」と「剰余群 $${\{idI,  \tau I\}}$$ が $${\tau I}$$ に関して巡回すること（巡回群になること）」を同一の構造とみることができます。同一の構造とみることによって、「差積 $${X_2}$$ の添加」を「剰余群 $${\{idI,  \tau I\}}$$ が巡回群になること」と結びつけることができます。後に重要になるので、このことを（＊）とします。

　「差積 $${X_2}$$ の添加」$${\leftrightarrow}$$「剰余群 $${\{idI,  \tau I\}}$$ が巡回群になること」　$${\cdots}$$（＊）

　次に、「体の拡大」と「群の縮小」の対応関係をみていきます。

「体の拡大」と「群の縮小」の対応

　体 $${Q_2}$$ は対称式の集合でした（本シリーズ (19)）。
　よって、$${Q_2}$$ 内のすべての式を変化させない置換は $${id}$$ と $${\tau}$$、つまり２次置換です。

　２次置換をすべて集めた集合は、２次対称群
　$${S_2=\{id,  \tau\}}$$
です（本シリーズ (34)）。これにより、体 $${Q_2}$$ と群 $${S_2=\{id,  \tau\}}$$ の対応関係が生まれます。

$$
\begin{align*}
体  Q_2  \xleftrightarrow[対応]{}  群  S_2=\{id,  \tau\}
\end{align*}
$$

　さらに、$${Q_2}$$ に
　$${X_2=\alpha-\beta}$$
を添加した拡大体を $${Q_2(X_2)}$$ とすると、その $${Q_2(X_2)}$$ 内のすべての式を変化させない置換は恒等置換 $${id}$$ のみです。添加された $${X_2}$$ は $${\tau}$$ で変化しますが、$${id}$$ では変化しません。

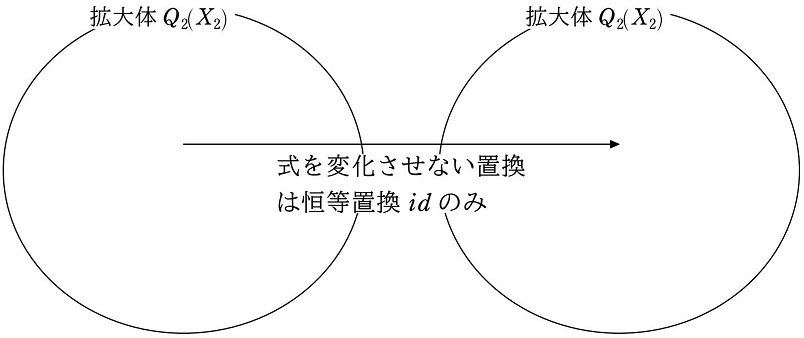
　$${id}$$ のみを要素とする集合
　$${I=\{id\}}$$
は、２次対称群 $${S_2}$$ の正規部分群です。これで、体 $${Q_2(X_2)}$$ と正規部分群 $${I}$$ の対応関係が生まれます。

$$
\begin{align*}
体  Q_2(X_2)  \xleftrightarrow[対応]{}  正規部分群  I=\{id\}
\end{align*}
$$

　これにより、「体の拡大」と「群の縮小」という、次のような対応関係が得られます。

$$
\begin{align*}
{\small \bm{＜体の拡大＞}}\hspace{8pt}Q_2&\hspace{-1pt}\overset{\bm{拡大}}{\subset} Q_2(X_2)\\
\Updownarrow{\scriptsize \bm{対応}}\hspace{-15pt}&\hspace{25pt}\Updownarrow {\scriptsize \bm{対応}}\\
{\small \bm{＜群の縮小＞}}\hspace{8pt}S_2\hspace{0pt}&\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_2 の正規部分群}{I}
\end{align*}
$$

　体が拡大するのに対応して群は縮小します。「拡大」と「縮小」で逆の関係になります。
　しかし、これだけだとただ対応させているだけなので、この対応を群構造の面から補強します。それが、先ほどやった（＊）の同一構造です。

　「差積 $${X_2}$$ の添加」$${\leftrightarrow}$$「剰余群 $${\{idI,  \tau I\}}$$ が巡回群になること」　$${\cdots}$$（＊）

「差積の添加」と「剰余群が巡回群」の対応

　この（＊）によって、単に「体の拡大」と「群の縮小」の対応ではなく、拡大と縮小の部分（接続部分）に、下図のような「解の差積 $${X_2}$$ の添加」と「剰余群 $${\{idI,  \tau I\}}$$ が巡回群になること」の構造的な対応が導かれます。この「差積」と「巡回群」の対応も含めた「体の拡大」と「群の縮小」の対応を『ガロア対応』といいます（下図）。　

$$
\begin{align*}
&\hspace{-10pt}{\footnotesize X_2  を添加 \Leftarrow (*)  の部分}\\[-3pt]
&\hspace{4pt}\downarrow\\
{\small \bm{＜体の拡大＞}}\hspace{8pt}Q_2&\hspace{-1pt}\overset{\bm{拡大}}{\subset} Q_2(X_2)\\
\Updownarrow{\scriptsize \bm{対応}}\hspace{-15pt}&\hspace{25pt}\Updownarrow {\scriptsize \bm{対応}}\\
{\small \bm{＜群の縮小＞}}\hspace{8pt}S_2\hspace{0pt}&\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_2 の正規部分群}{I}\\[-4pt]
&\hspace{4pt}\uparrow\\[-2pt]
&\hspace{-10pt}{\footnotesize \{idI,  \tau I\} \atop が巡回群} {\footnotesize  \Leftarrow (*)  の部分}
\end{align*}
$$

　解の差積 $${X_2}$$ の添加は平方根の添加に相当します。　
　また、次の章で詳しくやりますか、３次方程式についてのガロア対応は次のようになります。

$$
\begin{align*}
&\hspace{5pt}{\footnotesize X_3  を添加}\hspace{8pt}{\footnotesize A  を添加}\\[-4pt]
&\hspace{17pt}\downarrow\hspace{37pt}\downarrow\\[-2pt]
{\small \bm{＜体の拡大＞}}\hspace{10pt}&\hspace{-5pt}{\scriptsize Q_3(\omega)}\hspace{-2pt}\overset{\bm{拡大}}{\subset}\hspace{-5pt}{\scriptsize Q_3(\omega, X_3)}\hspace{-4pt}\overset{\bm{拡大}}{\subset}\hspace{-4pt}{\scriptsize Q_3(\omega, X_3, A)}\\[-3pt]
&\hspace{17pt}\Updownarrow\hspace{7pt}{\footnotesize 対応}\hspace{7pt}\Updownarrow\\[-2pt]
{\small \bm{＜群の縮小＞}}\hspace{10pt}&S_3\hspace{4pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_3 の正規部分群}{N}\hspace{-8pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny N の正規部分群}{I}\\[-4pt]
&\hspace{17pt}\uparrow\hspace{37pt}\uparrow\\[-2pt]
&\hspace{-4pt}{\footnotesize \{idN,  \tau_1N\} \atop が巡回群}\hspace{2pt}{\footnotesize \{idI,  \rho_2I,  \rho_3I\} \atop が巡回群}
\end{align*}
$$

　$${Q_3(\omega)}$$ を基礎体とし、３次方程式の３つの解の差積
　$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
の添加は平方恨の添加、ラグランジュ・リゾルベント
　$${A=\alpha+\omega\beta+\omega^2\gamma}$$
の添加は３乗根の添加に相当します（本シリーズ (13) 他）。
　そして、３乗根まで添加された拡大体 $${Q_3(\omega,  X_3,  A)}$$ 内で、３次方程式の解の公式は構成可能となります。

『可解群』について

　このことを踏まえると、解の公式が存在するかどうかは、上述の「群の構造」のみを調べればよいことがわかります。
　つまり、最初の群（２次対称群 $${S_2}$$ や３次対称群 $${S_3}$$）からスタートして、正規部分群による剰余類の集合（剰余群）が巡回群となるルールを保ちながら
　「 $${I＝\{id\}}$$ へといたる正規部分群の縮小の列」
が存在すれば、解の公式が存在するということです。
　例えば、２次方程式では、次のような「正規部分群の縮小の列」が存在します。上記のガロア対応の＜群の縮小＞のみを抜き出しています。

$$
\begin{align*}
{\small \bm{＜群の縮小＞}}\hspace{8pt}S_2\hspace{0pt}&\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_2 の正規部分群}{I}　\cdots (*3)\\[-4pt]
&\hspace{4pt}\uparrow\\[-2pt]
&\hspace{-10pt}{\footnotesize \{idI,  \tau I\} \atop が巡回群}
\end{align*}
$$

　同様に、３次方程式にも次のような「正規部分群の縮小の列」が存在します。これも、上記のガロア対応の＜群の縮小＞のみを抜き出しています。

$$
\begin{align*}
{\small \bm{＜群の縮小＞}}\hspace{10pt}&S_3\hspace{4pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny S_3 の正規部分群}{N}\hspace{-8pt}\overset{\bm{縮小}}{\supset}\hspace{-8pt}\underset{\tiny N の正規部分群}{I}　\cdots (*4)\\[-4pt]
&\hspace{17pt}\uparrow\hspace{37pt}\uparrow\\[-2pt]
&\hspace{-4pt}{\footnotesize \{idN,  \tau_1N\} \atop が巡回群}\hspace{2pt}{\footnotesize \{idI,  \rho_2I,  \rho_3I\} \atop が巡回群}
\end{align*}
$$

　この $${(*3),  (*4)}$$ のような
　「 $${I=\{id\}}$$ へといたる正規部分群の縮小の列」
をもつ群のことを『可解群』といいます。その方程式が可解である（解くことができる）群であるという意味です。ある群からスタートして、正規部分群による剰余類の集合（剰余群）が巡回群となるルールを保ちながら
　「 $${I＝\{id\}}$$ へといたる正規部分群の縮小の列」
が存在すれば、その群は可解群です。
　２方程式式の２つの解の置換を集めた集合は２次対称群
　$${S_2=\{id,  \tau\}}$$
となります。また、３次方程式の３つの解の置換を集めた集合は３次対称群
　$${S_3=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}}$$
となります（本シリーズ (28)）。
　解の公式が存在するかどうかは、その $${S_2}$$ や $${S_3}$$ のような解の置換の集合（対称群）が可解群になるかどうかによります。つまり

　$${S_2}$$ は可解群になるので、２次方程式に解の公式が存在する。
　$${S_3}$$ は可解群になるので、３次方程式に解の公式が存在する。

ということです。これが、２次方程式に解の公式が存在すること、３次方程式に解の公式が存在することの証明です。可解群かどうかという群の構造のみを考えれば、解の公式が存在するかどうかが判定できるのです。

　可解群とは、いわば
　「解の公式へといたる $${\{id\}}$$ への階段」
というイメージです。その階段の段差には「正規部分群による剰余群が巡回群になる」という決められたルールがあります（本シリーズ (33)）。可解群であるためには、必ずこのルールが必要です。
　このルールに従って、群が $${\{id\}}$$ まで縮小することができれば解の公式が存在する、群が $${\{id\}}$$ まで縮小することができなければ解の公式が存在しないということです。
　４次方程式については本シリーズでふれていませんが、４次対称群 $${S_4}$$ も可解群になるので、４次方程式には解の公式が存在します（余裕があれば４次方程式の解の公式にもふれます）。
　しかし、５次対称群 $${S_5}$$ は可解群ではありません。可解群ではないので、５次方程式には解の公式が存在しないことが証明されます。これが、ガロアによる証明の要点です。
　本シリーズの最終目標は、その
「５次対称群 $${S_5}$$ が可解群ではないこと」
です。その目標に向かって、順を追って解説していきます。

『ガロア拡大』『ガロア対応』『ガロア群』

　最後に、現代ガロア理論にあらわれる用語についてふれておきます。　
　大まかにいえば、この群構造をもつ体の拡大を『ガロア拡大』、ガロア拡大と群の縮小の対応を『ガロア対応』といいます。
　また、このガロア拡大から定義される群を『ガロア群』といいます。つまり
　基礎体 $${Q_2}$$ に対応するガロア群は $${\{id,  \tau\}}$$
　拡大体 $${Q_2(X_2)}$$ に対応するガロア群は $${\{id\}}$$
　ガロアの発見した理論なので、いろいろな場面でガロアの名前が冠されます（この辺りの用語は、きちんと定義しようとすると大学の教科書になるので、ここでは割愛します）。

最後に

　体の拡大は広くなる方向です。２次、３次と方程式の次数が高くなるほどその拡大は大きくなります。しかし、それと対応する群は縮小する方向です。縮小は $${\{id\}}$$ までとゴールが決まっています。
　いわば、広がりの大きくなる体の拡大を、ゴールが決まっている「群」の言葉にいいかえたことが、ガロアの斬新なアイデアといえます。

　さて、２次方程式だと、このガロアの証明の”ありがたみ”が分かりにくいかもしれません。３次方程式の解の公式以降で、ガロアによる群の理論が威力を発揮します。次の章ではそれをみていきます。

（参考）各章の内容

（１）「２次方程式の解の公式」を式変形で導出
　　　・平方完成
（２）「３次方程式の解の公式」を導出するための準備
　　　・$${1}$$ の３乗根 $${\omega}$$
（３）「３次方程式の解の公式」を式変形で導出
　　　・チルンハウス変換
（４）「解と係数の関係」と「対称式」の解説
（５）「対称式」を用いた「２次方程式の解の公式」の導出
（６）「解の置換」と「ラグランジュ・リゾルベント」の解説
（７）「ラグランジュ・リゾルベント」による「３次方程式の解の公式」の導出
（８）「遇置換」と「奇置換」の解説（ここから「アーベルの証明」の準備）
（９）「差積の２乗」が対称式となること、及び「差積」と平方根を結ぶ等式の証明。
（10）「平方根」「３乗根」と次々と累乗根を加えていくアイデア
（11）「アーベルの証明」のアイデアを用いて、なぜ「２次方程式の解の公式が存在するのか」を解説（添加する式について加筆予定）
（12）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（前編）。「差積の２乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む（対称性の破壊）。
（13）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（後編）。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む（対称性の破壊）。$${\longrightarrow}$$ ３次方程式の解の公式の完成
（14）「アーベルの証明」の解説①。５次方程式の解の差積（または差積の２乗の平方根）を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が５次置換（対称式）から遇置換シンメトリーへと破壊されることを解説。
（15）「アーベルの証明」の解説②。すべての置換は互換で表せることから、５次置換をすべて互換の積で表して、遇置換と奇置換に分類する。
（16）「アーベルの証明」の解説➂。「すべての遇置換は３次巡回置換の積で表される」ことの解説。
（17）「アーベルの証明」の解説➃（最後）。「任意の３次巡回置換が５次巡回置換の積で表せる」ことによって、５次方程式には解の公式が存在しないことが証明されることの解説。
（18）もっと分かりやすくシリーズ①「累乗根の添加」について重点解説。
（19）もっと分かりやすくシリーズ②「対称性の破壊」について重点解説。
（20）もっと分かりやすくシリーズ③「対称性を恒等置換まで破壊」することについて重点解説。
（21）もっと分かりやすくシリーズ➃　何次方程式でも「最初に解の差積を添加して対称性を破壊すること」は常套手段。
（22）もっと分かりやすくシリーズ➄「解の和と差の連立」による２次方程式の解の公式の導出について。
（23）もっと分かりやすくシリーズ➅「対称式ではない解の公式を基本対称式で表す」ことのついて。
（24）もっと分かりやすくシリーズ➆「定数 $${\bm{\omega}}$$」について復習
（25）もっと分かりやすくシリーズ➇　３次方程式の解の公式の導出方法「カルダノの方法」を復習
（26）もっと分かりやすくシリーズ➈「カルダノの方法」と「対称性の破壊」の関連について
（27）もっと分かりやすくシリーズ⑩　そもそもなぜ解の公式が存在しないかを『巡回置換』から紐解く
（28）中学でも分かるガロアの証明①　ガロアの発見した「群」について簡単に解説
（29）中学でも分かるガロアの証明①　ガロアの発見した「部分群」について簡単に解説
（30）中学でも分かるガロアの証明③　ガロアの発見した「正規部分群」について
（31）中学でも分かるガロアの証明➃　正規部分群による剰余類の集合が群（剰余群）になること
（32）中学でも分かるガロアの証明⑤　単位元のみの正規部分群 $${\{𝑖𝑑\}}$$ による剰余類の集合が群（剰余群）になること
（33）中学でも分かるガロアの証明⑥　「巡回群」について、および剰余群が巡回群になること
（34）中学でも分かるガロアの証明⑦　２次対称群で、正規部分群による剰余群が巡回群になることの復習
（35）中学でも分かるガロアの証明⑦　「体」について解説