
もっと分かりやすく➃「最初に差積を添加」して対称性を破壊
何次方程式であっても、最初に差積を添加して対称性を破壊することを解説していきます(本シリーズ (14))。
話の展開を分かりやすくするために、2次方程式の解の公式の導出を簡単に復習します(本シリーズ (1)、(18))。これは平方完成とよばれる方法です。
(復習)2次方程式の解の公式の導出
2次方程式 $${ax^2+bx+c=0}$$ を考えます。なお、簡単のため係数 $${a, b, c}$$ の範囲は有理数とします(注1で数の分類)。なお、2次方程式なので $${a\ne 0}$$ です。
まず、$${x^2}$$ の係数を $${1}$$ にするために両辺を $${a (\ne 0)}$$ で割って
$$
\begin{align*}
ax^2+bx+c&=0\\
\dfrac{\cancel{a}}{\cancel{a}}x^2+\dfrac{b}{a}x+\dfrac{c}{a}&=0\\
x^2+\dfrac{b}{a}x+\dfrac{c}{a}&=0
\end{align*}
$$
$${x}$$ の係数 $${\dfrac{b}{a}}$$ に着目。 それを $${2}$$ で割った $${\dfrac{b}{2a}}$$ の $${2}$$ 乗 $${\left(\dfrac{b}{2a}\right)^2}$$ を左辺に足して引いて
$$
\begin{align*}
x^2+\frac{b}{a}x\underbrace{+\left(\frac{b}{2a}\right)^2-\left(\frac{b}{2a}\right)^2}_{足して引いた}+\dfrac{c}{a}&=0\\
x^2+2\cdot\frac{b}{2a}x+\left(\frac{b}{2a}\right)^2-\left(\frac{b}{2a}\right)^2+\dfrac{c}{a}&=0
\end{align*}
$$
$${\dfrac{b}{2a}=A}$$ とおくと
$$
\begin{align*}
\underline{x^2+2Ax+A^2}-\left(\frac{b}{2a}\right)^2+\dfrac{c}{a}=0
\end{align*}
$$
公式『 $${x^2+2Ax+A^2=(x+A)^2}$$』(中学3年で習う因数分解)を用いて、下線部を因数分解して
$$
\begin{gather*}
\left(x+A\right)^2-\left(\dfrac{b}{2a}\right)^2+\dfrac{c}{a}=0
\end{gather*}
$$
$${A=\dfrac{b}{2a}}$$ に戻して
$$
\begin{gather*}
\left(x+\dfrac{b}{2a}\right)^2-\left(\dfrac{b}{2a}\right)^2+\dfrac{c}{a}=0
\end{gather*}
$$
これで、平方(2乗)の形 $${{(x+〇)}^2+\square=0}$$ を作ることができました。平方が完成したので、この変形を平方完成といいます。
ここで、$${-\left(\dfrac{b}{2a}\right)^2+\dfrac{c}{a}}$$ を右辺に移項して
$$
\begin{align*}
\left(x+\dfrac{b}{2a}\right)^2&=\left(\dfrac{b}{2a}\right)^2-\dfrac{c}{a}\\
&=\left(\dfrac{1}{2}\cdot\dfrac{b}{a}\right)^2-\dfrac{c}{a}\\
&=\left(\dfrac{1}{2}\right)^2\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}\\
&=\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}
\end{align*}
$$
より
$$
\begin{align*}
\left(x+\dfrac{b}{2a}\right)^2&=\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a} \cdots ①
\end{align*}
$$
ここで、両辺の平方恨をとって
$$
\begin{gather*}
x+\dfrac{b}{2a}=\pm\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}} \cdots ②
\end{gather*}
$$
$${\dfrac{b}{2a}}$$ を移項して
$$
\begin{gather*}
x=-\dfrac{b}{2a}\pm\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
\end{gather*}
$$
あとはこの式を整理して
$$
\begin{align*}
x&=-\dfrac{b}{2a}\pm\sqrt{\dfrac{1}{4}\left\{\left(\dfrac{b}{a}\right)^2-4\cdot\dfrac{c}{a}\right\}}\\
&=-\dfrac{b}{2a}\pm\sqrt{\left(\dfrac{1}{2}\right)^2\left\{\left(\dfrac{b}{a}\right)^2-4\cdot\dfrac{c}{a}\right\}}\\
&=-\dfrac{b}{2a}\pm\dfrac{1}{2}\sqrt{\left(\dfrac{b}{a}\right)^2-4\cdot\dfrac{c}{a}}\\
&=-\dfrac{b}{2a}\pm\dfrac{1}{2}\sqrt{\dfrac{b^2}{a^2}-\dfrac{4c}{a}}\\
&=-\dfrac{b}{2a}\pm\dfrac{1}{2}\sqrt{\dfrac{b^2}{a^2}-\dfrac{4ac}{a^2}}\\
&=-\dfrac{b}{2a}\pm\dfrac{1}{2}\sqrt{\dfrac{b^2-4ac}{a^2}}\\
&=-\dfrac{b}{2a}\pm\dfrac{1}{2}\cdot\dfrac{\sqrt{b^2-4ac}}{\sqrt{a^2}}\\
&=-\dfrac{b}{2a}\pm\dfrac{1}{2}\cdot\dfrac{\sqrt{b^2-4ac}}{a}\\
&=-\dfrac{b}{2a}\pm\dfrac{\sqrt{b^2-4ac}}{2a}\\
&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{align*}
$$
より
$$
\begin{align*}
x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{align*}
$$
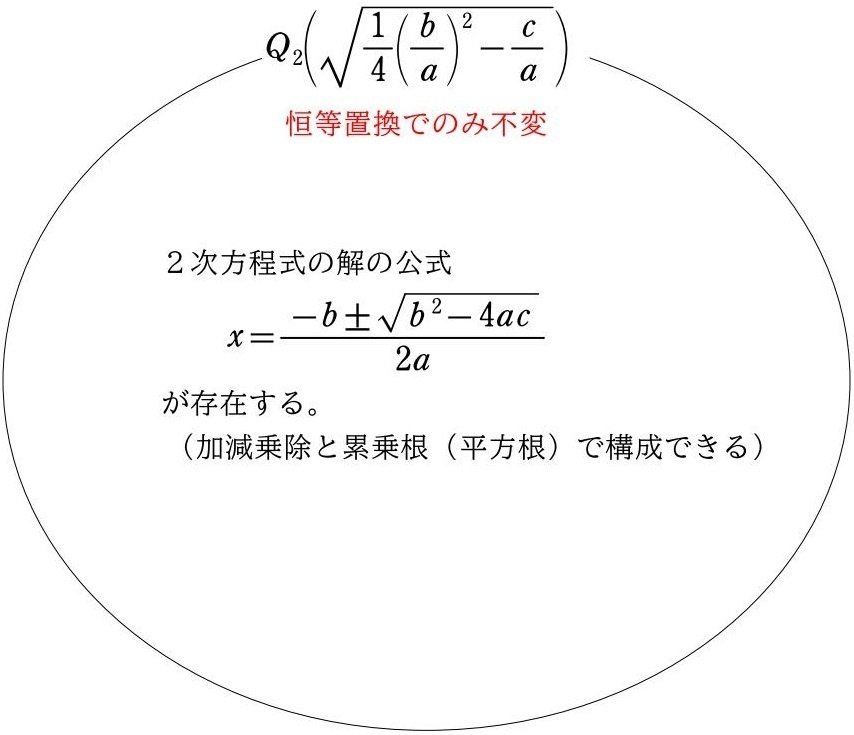
これで2次方程式の解の公式が、教科書で見られる形で導出されます。2次方程式の解の公式は、係数の加減乗除だけで構成することはできず、平方根が必要です。
(復習)平方根の添加
平方根を取るという操作は、上記の $${➀}$$ から $${②}$$ の計算過程
(再掲)
$$
\begin{align*}
\left(x+\dfrac{b}{2a}\right)^2&=\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a} \cdots ①
\end{align*}
$$
ここで、両辺の平方恨をとって
$$
\begin{gather*}
x+\dfrac{b}{2a}=\pm\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}} \cdots ②
\end{gather*}
$$
(再掲終わり)
という計算部分に現れます。$${➀}$$ の右辺
$$
\begin{align*}
\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a} \cdots ③
\end{align*}
$$
までは係数と有理数の加減乗除だけで計算できます。しかし、平方根を取るという操作の入った $${②}$$ の右辺
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}} \cdots ➃
\end{align*}
$$
は、加減乗除だけでは計算できません。そこで、$${➃}$$ を新しい式として添加(係数の加減乗除で構成できるすべての式の集合に添加)することによって、$${②}$$ への式変形を可能にします(本シリーズ (18))。新しい式である「平方根の添加」によって、2次方程式の解の公式は導出可能となります。
ここで、この $${➃}$$ 式を<解と係数の関係>と結びつけます。
2次方程式 $${ax^2+bx+c=0}$$ について、2つの解を $${\alpha, \beta}$$ とすると、次のことが成り立ちます。
<解と係数の関係>
$$
\begin{align*}
\alpha+\beta&=-\dfrac{b}{a}\\
\alpha\beta&=\dfrac{c}{a}
\end{align*}
$$
これより、この関係式の両辺を入れ替えて
$$
\begin{align*}
-\dfrac{b}{a}&=\alpha+\beta\\[8pt]
\dfrac{c}{a}&=\alpha\beta
\end{align*}
$$
上の式の両辺に $${-1}$$ をかけて
$$
\begin{align*}
\dfrac{b}{a}&=-(\alpha+\beta)\\[8pt]
\dfrac{c}{a}&=\alpha\beta
\end{align*}
$$
すると、係数の分数 $${\dfrac{b}{a}, \dfrac{c}{a}}$$ は対称式で表されることがわかります。これらを、先ほどの $${③}$$ 式
$$
\begin{align*}
\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a} \cdots ③
\end{align*}
$$
に代入すると
$$
\begin{align*}
\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}
&=\dfrac{1}{4}\left\{-(\alpha+\beta)\right\}^2-\alpha\beta\\
&=\dfrac{1}{4}\left(\alpha+\beta\right)^2-\alpha\beta\\
&=\dfrac{1}{4}\left(\alpha+\beta\right)^2-\dfrac{4}{4}\alpha\beta\\
&=\dfrac{\left(\alpha+\beta\right)^2-4\alpha\beta}{4}\\
&=\dfrac{\alpha^2+2\alpha\beta+\beta^2-4\alpha\beta}{4}\\
&=\dfrac{\alpha^2+2\alpha\beta-4\alpha\beta+\beta^2}{4}\\
&=\dfrac{\alpha^2-2\alpha\beta+\beta^2}{4}\\
&=\dfrac{(\alpha-\beta)^2}{4}
\end{align*}
$$
より
$$
\begin{align*}
\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}
&=\dfrac{(\alpha-\beta)^2}{4}
\end{align*}
$$
ここで、この式の平方根を取ると
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
&=\sqrt{\dfrac{(\alpha-\beta)^2}{4}}\\
&=\sqrt{\dfrac{1}{4}(\alpha-\beta)^2}\\
&=\sqrt{\left(\dfrac{1}{2}\right)^2(\alpha-\beta)^2}\\
&=\dfrac{1}{2}\sqrt{(\alpha-\beta)^2}
\end{align*}
$$
より
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
&=\dfrac{1}{2}\sqrt{(\alpha-\beta)^2} \cdots ➄
\end{align*}
$$
ここで、本シリーズ (18) で
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
\end{align*}
$$
の添加によって、2次方程式の解の公式が構成可能となることを勉強しましたが、それに代えて
$$
\begin{align*}
\sqrt{(\alpha-\beta)^2}
\end{align*}
$$
を添加しても、2次方程式の解の公式が構成可能となります。以下、その理由を述べていきます。
「差積の2乗の平方根」を添加してもよいこと
まず
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
\end{align*}
$$
を添加すると、$${➄}$$ 式
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
&=\dfrac{1}{2}\sqrt{(\alpha-\beta)^2} \cdots ➄
\end{align*}
$$
より、それとイコールである
$$
\begin{align*}
\dfrac{1}{2}\sqrt{(\alpha-\beta)^2}
\end{align*}
$$
を添加することと同じとなり、これを2倍(有理数倍)すると
$$
\begin{align*}
\dfrac{1}{2}\sqrt{(\alpha-\beta)^2}\times2=\sqrt{(\alpha-\beta)^2}
\end{align*}
$$
より、$${\sqrt{(\alpha-\beta)^2}}$$ が構成できるので
$$
\begin{align*}
\sqrt{(\alpha-\beta)^2}
\end{align*}
$$
を添加することと同じになります。途中2倍(有理数倍)していますが、有理数倍はもともと許された計算なので自由に行ってもかまいません(平方根を取る操作は加減乗除ではないのでダメ)(本シリーズ (18))。
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}} の添加
\longrightarrow \sqrt{(\alpha-\beta)^2} の添加
\end{align*}
$$
逆に
$$
\begin{align*}
\sqrt{(\alpha-\beta)^2}
\end{align*}
$$
を添加すると、それを $${\dfrac{1}{2}}$$ 倍(有理数倍)して
$$
\begin{align*}
\dfrac{1}{2}\sqrt{(\alpha-\beta)^2}
\end{align*}
$$
が構成できるので、$${➄}$$ 式
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
&=\dfrac{1}{2}\sqrt{(\alpha-\beta)^2} \cdots ➄
\end{align*}
$$
より、それとイコールである
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
\end{align*}
$$
を添加すること同じとなります。途中 $${\dfrac{1}{2}}$$ 倍が入りますが、有理数倍はもともと許された計算なので、自由に行っても構いません。
$$
\begin{align*}
\sqrt{(\alpha-\beta)^2} の添加 \longrightarrow \sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}} の添加
\end{align*}
$$
以上より
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}} の添加
\longrightarrow \sqrt{(\alpha-\beta)^2} の添加
\end{align*}
$$
と
$$
\begin{align*}
\sqrt{(\alpha-\beta)^2} の添加 \longrightarrow \sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}} の添加
\end{align*}
$$
の両方が証明されたので
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}} の添加 \longleftrightarrow \sqrt{(\alpha-\beta)^2} の添加 \cdots (*1)
\end{align*}
$$
この $${(*1)}$$ より、添加する式
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}
\end{align*}
$$
の代わりに、2次方程式の解 $${\alpha, \beta}$$ を用いた式
$$
\begin{align*}
\sqrt{(\alpha-\beta)^2}
\end{align*}
$$
を添加してもよいことがわかります(なお、$${\longleftrightarrow}$$ は同値であることを意味し、$${\longrightarrow}$$ とその逆 $${\longleftarrow}$$ の両方が証明されて初めて同値となる)。
カギとなるのは差積
$${X_2=\alpha-\beta}$$
です。その「差積の2乗の平方根」
$${\sqrt{(X_2)^2}=\sqrt{(\alpha-\beta)^2}}$$
を添加すれば、2次方程式の解の公式が構成できることになります。
さらに、次のように考えれば、シンプルに差積 $${X_2}$$ を添加すればよいことも分かります。
「差積そのもの」を添加してもよいこと
まず、次のように平方根を外すことができます(注2で証明)。
$$
\begin{align*}
\sqrt{(\alpha-\beta)^2}
&=
\begin{cases}
\alpha-\beta \cdots ➅\\
-(\alpha-\beta) \cdots ➆
\end{cases}
\end{align*}
$$
まず $${\sqrt{(\alpha-\beta)^2}}$$ を添加すると、$${➅}$$ より $${\alpha-\beta}$$ を添加すること同じになります。$${➆}$$ より $${-(\alpha-\beta)}$$ も合わせて添加されますが、差積
$${X_2=\alpha-\beta}$$
が添加されたことで目標達成です。
$$
\begin{align*}
\sqrt{(\alpha-\beta)^2} の添加 \longrightarrow \alpha-\beta の添加
\end{align*}
$$
逆に、$${X_2=\alpha-\beta}$$ を添加すると、それを $${-1}$$ 倍(有理数倍)すると $${-(\alpha-\beta)}$$ も構成できるので、$${➅}$$、$${➆}$$ より、それとイコールである $${\sqrt{(\alpha-\beta)^2}}$$ を添加することと同じになります。
$$
\begin{align*}
\alpha-\beta の添加 \longrightarrow \sqrt{(\alpha-\beta)^2} の添加
\end{align*}
$$
以上より
$$
\begin{align*}
\sqrt{(\alpha-\beta)^2} の添加 \longrightarrow \alpha-\beta の添加
\end{align*}
$$
と
$$
\begin{align*}
\alpha-\beta の添加 \longrightarrow \sqrt{(\alpha-\beta)^2} の添加
\end{align*}
$$
の両方が証明されたので
$$
\begin{align*}
\sqrt{(\alpha-\beta)^2} の添加 \longleftrightarrow \alpha-\beta の添加 \cdots (*2)
\end{align*}
$$
よって、$${(*1), (*2)}$$
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}} の添加
&\longleftrightarrow \sqrt{(\alpha-\beta)^2} の添加 \cdots (*1)\\[20pt]
\sqrt{(\alpha-\beta)^2} の添加
&\longleftrightarrow \alpha-\beta の添加 \cdots (*2)
\end{align*}
$$
より
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}} の添加
\longleftrightarrow \sqrt{(\alpha-\beta)^2} の添加
\longleftrightarrow \alpha-\beta の添加\\
\cdots (*3)
\end{align*}
$$
以上により、
$${\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}}$$ を添加することと、
$${\sqrt{(\alpha-\beta)^2}}$$(差積の2乗の平方根)を添加することと、
$${\alpha-\beta}$$(差積そのもの)を添加することは同じとなります。
このことから、差積を添加することは平方根を添加することと同じであることが分かります。
「差積の添加」=「平方根の添加」
差積 $${X_2=\alpha-\beta}$$ の添加によって、加減乗除という枠を乗り越え、平方根という新たな武器(計算)が使えるようになり、2次方程式の解の公式を得ることができます。
さて、2次方程式の係数 $${a, b, c}$$ と有理数の加減乗除で構成できるすべての式の集合 $${Q_2}$$ について、その集合は、すべての対称式の集合になることはすでにやりました(本シリーズ (19))。

ここで、
$${Q_2}$$ に $${\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}}$$ を添加した集合を $${Q_2\left(\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}\right)}$$
$${Q_2}$$ に $${\sqrt{(\alpha-\beta)^2}}$$ を添加した集合を $${Q_2(\sqrt{(\alpha-\beta)^2})}$$
$${Q_2}$$ に $${\alpha-\beta}$$ を添加した集合を $${Q_2(\alpha-\beta)}$$
とすると、先ほどやった $${(*3)}$$
$$
\begin{align*}
\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}} の添加
\longleftrightarrow \sqrt{(\alpha-\beta)^2} の添加
\longleftrightarrow \alpha-\beta の添加\\
\cdots (*3)
\end{align*}
$$
より、この3つの集合は同じ集合となります。同じという意味は、その集合内で構成可能な式の範囲が同じになるということです。
$$
\begin{align*}
Q_2\left(\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}\right)
=Q_2(\sqrt{(\alpha-\beta)^2})=Q_2(\alpha-\beta)
\end{align*}
$$

本シリーズ (18) で、集合 $${Q_2\left(\sqrt{\dfrac{1}{4}\left(\dfrac{b}{a}\right)^2-\dfrac{c}{a}}\right)}$$ 内で構成できるすべての式の対称性(構成できるすべての式を変化せない置換)は恒等置換のみなので、その集合内で2次方程式の解の公式が構成可能となることをやりました。
(図説)本シリーズ (19) から再掲
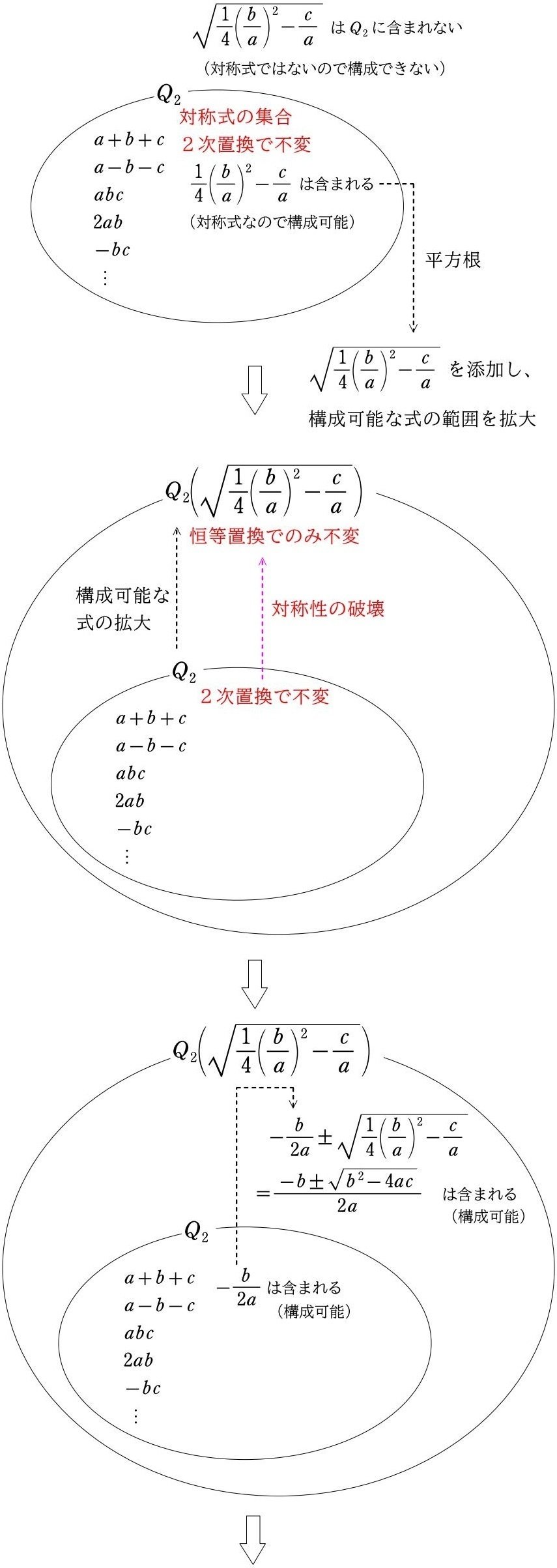
ここで、差積の2乗 $${(\alpha-\beta)^2}$$ の対称性を考えます。$${(\alpha-\beta)^2}$$ は、$${\alpha}$$ と $${\beta}$$ を入れ替えても変化しないので対称式です。2乗なので、符号が変わっても同じ式となります。
$$
\begin{align*}
&(\alpha-\beta)^2\\
&\hspace{11pt}\downarrow {\small \alpha と \beta を入れ替え}\\
&(\beta-\alpha)^2\\
=\,&(-\alpha+\beta)^2\\
=\,&\{-(\alpha-\beta)\}^2\\
=\,&(\alpha-\beta)^2(変化しない)
\end{align*}
$$
よって、対称式である $${(\alpha-\beta)^2}$$ は、すべての対称式の集合である $${Q_2}$$ 内で構成可能です。
一方、$${\sqrt{(\alpha-\beta)^2}}$$ や $${\alpha-\beta}$$ は対称式ではありません。$${\alpha}$$ と $${\beta}$$ を入れ替えると式は変化します(注2、注3で証明)。
すると
集合 $${Q_2}$$ に $${\sqrt{(\alpha-\beta)^2}}$$ を添加した集合 $${Q_2(\sqrt{(\alpha-\beta)^2})}$$
集合 $${Q_2}$$ に $${\alpha-\beta}$$ を添加した集合 $${Q_2(\alpha-\beta)}$$
では、その集合内で構成できるすべての式の対称性(構成できるすべての式を変化させない置換)は恒等置換のみとなるので、恒等置換と同等の対称性をもつ2次方程式の解の公式が、これらの集合
$${Q_2(\sqrt{(\alpha-\beta)^2})}$$
や
$${Q_2(\alpha-\beta)}$$
内で構成可能となります。
(図説)$${\sqrt{(\alpha-\beta)^2}}$$ を添加すると


(図説)$${\alpha-\beta}$$ を添加すると
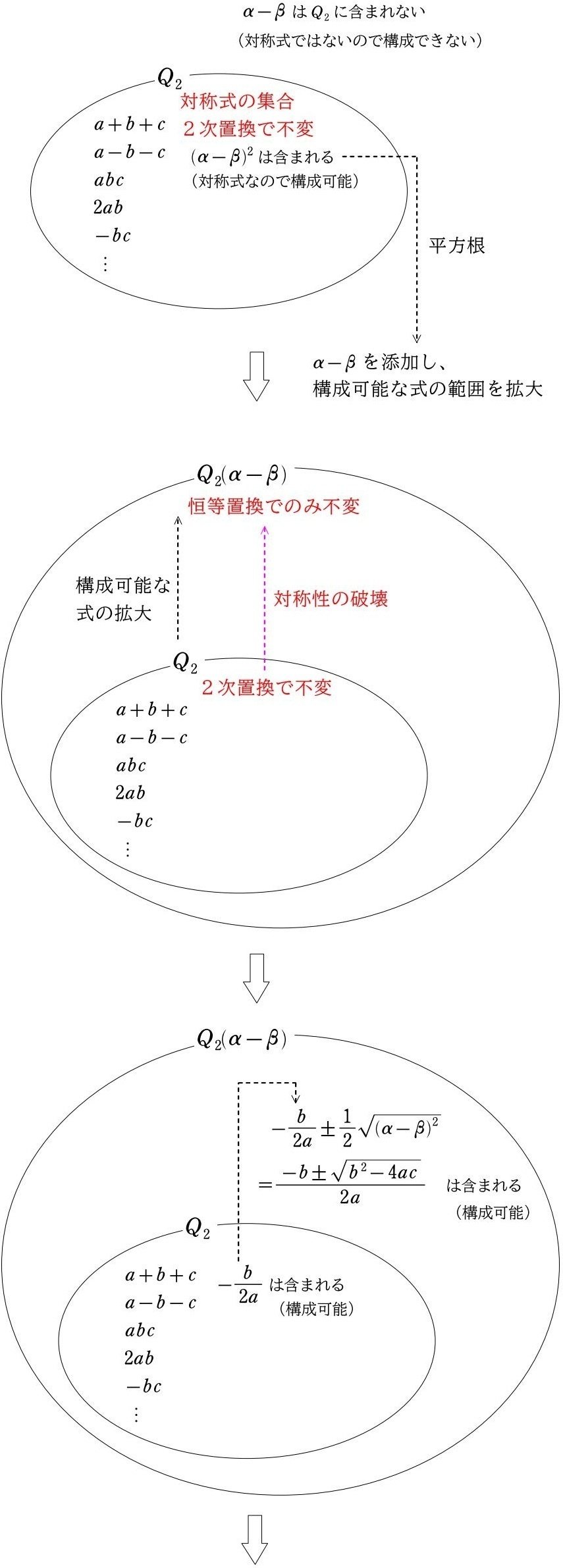

以上のように、添加する式は必ずも1通りではなく、解の公式を構成する上で都合のよい式、つまり対称性を破壊できる式なら何を添加しても構いません。2次方程式の場合、解を用いた式として、$${\sqrt{(\alpha-\beta)^2}}$$ を添加しても、$${\alpha-\beta}$$ を添加しても、どちらでも2次方程式の解の公式を構成できるわけです。
極端なはなし、$${2}$$ 倍した $${2(\alpha-\beta)}$$ や、$${3}$$ を足した $${(\alpha-\beta)+3}$$ などを添加してもよいわけですが、無意味な計算を入れる必要はないので、普通は $${\alpha-\beta}$$ を添加することで十分です。
初めに差積を添加するのは常套手段
実は、最初に差積を添加して対称性を破壊することは、何次方程式であっても解の公式を構成する上で常套手段となります。
2次方程式の解の差積は
$${X_2=\alpha-\beta}$$
です。$${(X_2)^2}$$ は対称式ですが、差積そのもの $${X_2}$$ は対称式ではありません。この差積を添加し、構成可能な式の対称性を2次置換から恒等置換に破壊することによって、2次方程式の解の公式が構成できるようになります(本シリーズ (11)、(19))。
3次方程式の解を $${\alpha, \beta, \gamma}$$ とすると、その差積は
$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
です。文字通り、解の差のすべての積となります。$${(X_3)^2}$$ は対称式ですが、差積そのもの $${X_3}$$ は対称式ではありません。
最初にこの差積を添加することによって、構成可能な式の対称性を3次置換(3つの解のすべての入れ替え)から遇置換(遇置換シンメトリー)に破壊します(本シリーズ (12)、(13))。
そして、詳しくは本シリーズ (13) にゆずりますが、さらにラグランジュ・リゾルベント
$${A=\alpha+\omega\beta+\omega^2\gamma}$$
の添加によって、構成可能な式の対称性を恒等置換にまで破壊することができ、それによって3次方程式の解の公式は構成可能となります。
4次方程式の解を $${x_1, x_2, x_3, _4}$$ とすると、その差積は
$$
\begin{align*}
X_4=(x_1-x_2)(x_1-x_3)(x_1-x_4)&\\
\cdot\,(x_2-x_3)(x_2-x_4)&\\
\cdot\,(x_3-x_4)&
\end{align*}
$$
です。3次方程式と同様、解の差のすべての積となります。$${(X_4)^2}$$ は対称式ですが、差積そのもの $${X_4}$$ は対称式ではありません。
本シリーズでは4次方程式は解説していませんが、3次方程式同様、最初にこの差積を添加することによって、構成可能な式の対称性を4次置換(4つの解のすべての入れ替え)から遇置換(遇置換シンメトリー)に破壊します。その後、4次方程式のラグランジュ・リゾルベントなど必要な式を次々と添加することによって、構成可能な式の対称性を恒等置換にまで破壊することができ、それによって4次方程式の解の公式は構成可能となります(具体的な証明は割愛)。
5次方程式の解を $${x_1, x_2, x_3, x_4, x_5}$$ とすると、その差積は
$$
\begin{align*}
X_5=x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&\
\end{align*}
$$
です。3次方程式、4次方程式と同様、解の差のすべての積となります。$${(X_5)^2}$$ は対称式ですが、差積そのもの $${X_5}$$ は対称式ではありません。
3次方程式同様、最初にこの差積を添加することによって、構成可能な式の対称性を5次置換(5つの解のすべての入れ替え)から遇置換(遇置換シンメトリー)に破壊できます(本シリーズ (14))。
このように、何次方程式でも差積を構成することができ、その差積の添加によって、構成可能な式の対称性を遇置換シンメトリーまで破壊することができます。しかし5次以上の方程式の場合、その破壊は遇置換シンメトリーまででそれ以上破壊できない。つまり恒等置換まで破壊できないことによって、5次以上の方程式には解の公式は存在しないと帰結できる、というのが本シリーズで証明している内容です(アーベル・ルフィニの定理)(本シリーズ (14)~(17))。
(注1)数の分類
数の分類は以下の通りです。
$$
\begin{align*}
\boldsymbol{複素数 a+bi}
\begin{cases}
\overset{\small b=0 のとき}{\boldsymbol{実数 a}}
\begin{cases}
\underset{\scriptsize 分数で表せる数}{\boldsymbol{有理数}}
\begin{cases}
\boldsymbol{整数}
\begin{cases}
\boldsymbol{自然数} \scriptsize{(1, 2, 3, \cdots)}\\
\boldsymbol{0}\\
\boldsymbol{負の整数} \scriptsize{(-1, -2, -3, \cdots)}
\end{cases}\\
\boldsymbol{有限小数}\\
{\footnotesize 例 0.17 (=\dfrac{17}{100})}\\
\boldsymbol{循環小数{\scriptsize(循環する無限小数)}}\\
{\footnotesize 例 0.232323\cdots\left(=\dfrac{23}{99}\right)}
\end{cases}\\
\underset{\scriptsize 分数で表せない数}{\boldsymbol{無理数}}\\
{\scriptsize 例 \pi (=3.1415\cdots) のような \boldsymbol{循環しない無限小数}}\\
{\scriptsize e (=2.7182\cdots) のような \boldsymbol{循環しない無限小数}}\\
\end{cases}\\
\overset{\small b\ne0 のとき}{\boldsymbol{虚数 a+bi}} 特に a=0 のとき \boldsymbol{bi} を\boldsymbol{純虚数}という。
\end{cases}
\end{align*}
$$
(注2)平方根を外す公式を簡単に説明
$$
\begin{align*}
\sqrt{(\alpha-\beta)^2}
&=
\begin{cases}
\alpha-\beta\\
-(\alpha-\beta)
\end{cases}
\end{align*}
$$
について、厳密な証明には高校で習う複素数のいろいろな知識が必要ですが、ここでは簡単に説明します。
$${\sqrt{(\alpha-\beta)^2}}$$ は
「2乗すると $${(\alpha-\beta)^2}$$ となる複素数」
を表します。$${\sqrt{2}}$$ は
「2乗すると $${\sqrt{2}}$$ となる正の実数」
であることと同じ意味合いです。
なお、$${\sqrt{2}}$$ は正の実数でしたが、$${\sqrt{(\alpha-\beta)^2}}$$ は複素数の範囲で考えています(複素数には正や負の概念はないので、正の複素数、負の複素数という概念はありません)。
2次方程式の解 $${\alpha, \beta}$$ は一般には複素数なので、その $${\alpha, \beta}$$ の加減乗除で構成される $${(\alpha-\beta)^2}$$ も一般には複素数です。すると
「2乗すると $${(\alpha-\beta)^2}$$ となる複素数」
は、一般には $${\alpha-\beta}$$ と $${-(\alpha-\beta)}$$ の2つあります。
$$
\begin{align*}
\alpha-\beta &\xrightarrow{2乗}{} (\alpha-\beta)^2\\
-(\alpha-\beta) &\xrightarrow{2乗}{} \{-(\alpha-\beta)\}^2=(\alpha-\beta)^2
\end{align*}
$$
よって、その2つを取り得る値として
$$
\begin{align*}
\sqrt{(\alpha-\beta)^2}
&=
\begin{cases}
\alpha-\beta\\
-(\alpha-\beta)
\end{cases}
\end{align*}
$$
となります。
(コメント)ちょっと怪しいことを書いているかもしれないで、訂正があれば書き直します。
(注3)差積の2乗の平方根が対称式ではないことの証明
本シリーズ (19) で既に述べてありますが、改めてここでも証明します。表記の仕方がその時によっていろいろ違うので、後に分かりやすい方で統一したいと思います。
(証明)
差積の2乗の平方根 $${\sqrt{(\alpha-\beta)^2}}$$ が、$${\alpha}$$ と $${\beta}$$ の入れ替えで変化することを示す。まず、平方根を外すと
$$
\begin{align*}
\sqrt{(\alpha-\beta)^2}
&=
\begin{cases}
\alpha-\beta\\
-(\alpha-\beta)
\end{cases}
\end{align*}
$$
より、
(case1) $${\sqrt{(\alpha-\beta)^2}=\alpha-\beta}$$ のとき
$$
\begin{align*}
&\alpha-\beta\\
&\hspace{7.5pt}\downarrow {\small \alpha と \beta を入れ替え}\\
&\beta-\alpha(変化する)
\end{align*}
$$
(case2) $${\sqrt{(\alpha-\beta)^2}=-(\alpha-\beta)}$$ のとき
$$
\begin{align*}
-&(\alpha-\beta)\\
&\hspace{10.5pt}\downarrow {\small \alpha と \beta を入れ替え}\\
-&(\beta-\alpha)(変化する)
\end{align*}
$$
よって、$${\sqrt{(\alpha-\beta)^2}}$$ は対称式ではない。
(注4)差積が対称式ではないことの証明
上記の (case1) がその証明となります。
(参考)各章の内容
(1)「2次方程式の解の公式」を式変形で導出
・平方完成
(2)「3次方程式の解の公式」を導出するための準備
・$${1}$$ の3乗根 $${\omega}$$
(3)「3次方程式の解の公式」を式変形で導出
・チルンハウス変換
(4)「解と係数の関係」と「対称式」の解説
(5)「対称式」を用いた「2次方程式の解の公式」の導出
(6)「解の置換」と「ラグランジュ・リゾルベント」の解説
(7)「ラグランジュ・リゾルベント」による「3次方程式の解の公式」の導出
(8)「遇置換」と「奇置換」の解説(ここから「アーベルの証明」の準備)
(9)「差積の2乗」が対称式となることを解説
(10)「平方根」「3乗根」と次々と累乗根を加えていくアイデア
(11)「アーベルの証明」のアイデアを用いて、なぜ「2次方程式の解の公式が存在するのか」を解説(添加する式について加筆予定)
(12)「アーベルの証明」のアイデアを用いて、なぜ「3次方程式の解の公式が存在するのか」を解説(前編)。「差積の2乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む(対称性の破壊)。
(13)「アーベルの証明」のアイデアを用いて、なぜ「3次方程式の解の公式が存在するのか」を解説(後編)。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む(対称性の破壊)。$${\longrightarrow}$$ 3次方程式の解の公式の完成
(14)「アーベルの証明」の解説①。5次方程式の解の差積(または差積の2乗の平方根)を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が5次置換(対称式)から遇置換シンメトリーへと破壊されることを解説。
(15)「アーベルの証明」の解説②。すべての置換は互換で表せることから、5次置換をすべて互換の積で表して、遇置換と奇置換に分類する。
(16)「アーベルの証明」の解説➂。「すべての遇置換は3次巡回置換の積で表される」ことの解説。
(17)「アーベルの証明」の解説➃(最後)。「任意の3次巡回置換が5次巡回置換の積で表せる」ことによって、5次方程式には解の公式が存在しないことが証明されることの解説。
(18)もっと分かりやすくシリーズ①「累乗根の添加」について重点解説。
(19)もっと分かりやすくシリーズ②「対称性の破壊」について重点解説。
(20)もっと分かりやすくシリーズ③「対称性を恒等置換まで破壊」することについて重点解説。
(21)もっと分かりやすくシリーズ➃ 何次方程式でも「最初に解の差積を添加して対称性を破壊すること」は常套手段。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
