（図版追加）『巡回群』について、および剰余群が巡回群になること

巡回群について

　ここでは、重要な巡回群について解説します。巡回群とは「すべての要素が、あるひとつの要素だけを用いて表すことのできる群」です。具体的には、これまで何度も現れた、３次対称群
　$${S_3=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}}$$
の正規部分群である３次交代群
　$${N=\{id,  \rho_2,  \rho_3\}}$$
が巡回群になります。$${S_3}$$ の遇置換だけをすべて集めた群です（本シリーズ (30)）。このことを今から解説します。
　なお、一般に３次交代群は $${A_3}$$ と表しますが、ここでは $${S_3}$$ の正規部分群ということで、$${N}$$ という記号で表記しています。normal subgroup（正規部分群）の頭文字です。

３次交代群が巡回群になること

　まず、$${N=\{id,  \rho_2,  \rho_3\}}$$ の要素同士について、その置換の合成（積）の演算表

$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-11pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
    & id & \utilde{\underline{\rho_2}} & \rho_3\\ \hline\hline
id & id & \rho_2 & \rho_3\\ \hline
\underline{\rho_2} & \rho_2 & \underline{\rho_3} & id\\ \hline
\utilde{\rho_3} & \rho_3 & \utilde{id} & \rho_2
\end{array}
$$

より
　$${\rho_2\rho_2=\underline{\rho_3}　\cdots (*1)}$$（下線部）
　$${\rho_3\rho_2=\utilde{id}　\cdots (*2)}$$（波線部）

　ここで、同じものの置換の積を
　$${\rho_2\rho_2={(\rho_2)}^2　\cdots (*3)}$$
　$${\rho_2\rho_2\rho_2={(\rho_2)}^3　\cdots (*4)}$$
$${\hspace{45pt}\vdots   {\small 以下同様}}$$
と定義します。

　なお、$${(*4)}$$ に関して、$${N}$$ は群であるため、交換法則
　$${(\rho_2\rho_2)\rho_2=\rho_2(\rho_2\rho_2)}$$
が成り立ちます。交換法則よりどこから演算をしても結果は変わらないので、これを単に
　$${(\rho_2\rho_2)\rho_2=\rho_2(\rho_2\rho_2)=\rho_2\rho_2\rho_2}$$
と表し、それを
　$${\rho_2\rho_2\rho_2={(\rho_2)}^3}$$
と表記しています。一般に、群の要素について、同じものの２つの積は２乗、同じものの３つの積は３乗、$${\cdots}$$、と累乗で表記します。
　すると

$$
\begin{alignat*}{2}
id&=\rho_3\rho_2 &　&{\small (*2) より}\\
&=(\rho_2\rho_2)\rho_2 &　&{\small (*1) より}\\
&=\rho_2\rho_2\rho_2 &　&{\small 結合法則より}\\
&={(\rho_2)}^3 &　&{\small (*4) より}\\[10pt]
\rho_3&=\rho_2\rho_2 &　&{\small (*1) より}\\
&={(\rho_2)}^2 &　&{\small (*3) より}
\end{alignat*}
$$

より

$$
\begin{align*}
id&={(\rho_2)}^3\\
\rho_3&={(\rho_2)}^2
\end{align*}
$$

よって

$$
\begin{align*}
N&=\{id,  \rho_2,  \rho_3\}\\
&=\{{(\rho_2)}^3,  \rho_2,  {(\rho_2)}^2\}\\
&=\{\rho_2,  {(\rho_2)}^2,  {(\rho_2)}^3\}
\end{align*}
$$

　これで、$${N}$$ の要素のすべてを、ひとつの要素 $${\rho_2}$$ だけを用いて表すことができました。この $${N}$$ のように「すべての要素が、あるひとつの要素だけを用いて表せる群」を巡回群といいます。このとき、この $${\rho_2}$$ を $${N}$$ の生成元といいます。
　また、$${\rho_2}$$ が生成元となる巡回群を $${\langle\rho_2\rangle}$$ と表します。つまり

$$
\begin{align*}
N&=\{id,  \rho_2,  \rho_3\}\\
&=\{\rho_2,  {(\rho_2)}^2,  {(\rho_2)}^3\}\\
&=\langle\rho_2\rangle
\end{align*}
$$

　一般に、生成元を $${a}$$ とする巡回群を $${\langle a\rangle}$$ と表します。
　この $${N=\{id,  \rho_2,  \rho_3\}}$$ は、$${\rho_2}$$ に次々と $${\rho_2}$$ を作用させていけば、その要素は巡回的にすべて現れます。

$$
\begin{align*}
&\rho_2\\
&\downarrow  {\small \rho_2  を作用}\\
\rho_2\rho_2=\;&\rho_3\\
&\downarrow  {\small \rho_2  を作用}\\
\rho_3\rho_2=\;&id\\
&\downarrow  {\small \rho_2  を作用}\\
id\rho_2=\;&\rho_2\\
&\downarrow  {\small \rho_2  を作用}\\
\rho_2\rho_2=\;&\rho_3\\
&\downarrow  {\small \rho_2  を作用}\\
\rho_3\rho_2=\;&id\\
&\downarrow  {\small \rho_2  を作用}\\
id\rho_2=\;&\rho_2\\
&\downarrow  {\small 以下繰り返し}\\
&\hspace{4pt}\vdots 
\end{align*}
$$

　つまり

　円で描くと

　ちなみに、$${N}$$ の要素同士の置換の合成（積）の演算表

$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-11pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
    & id & \utilde{\underline{\rho_2}} & \rho_3\\ \hline\hline
id & id & \rho_2 & \rho_3\\ \hline
\underline{\rho_2} & \rho_2 & \underline{\rho_3} & id\\ \hline
\utilde{\rho_3} & \rho_3 & \utilde{id} & \rho_2
\end{array}
$$

を、生成元 $${\rho_2}$$ だけで表すと次のようになります。

$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-11pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
    & id & \rho_2 & \rho_3\\ \hline\hline
id & {(\rho_2)}^3 & \rho_2 & {(\rho_2)}^2\\ \hline
\rho_2 & \rho_2 & {(\rho_2)}^2 & {(\rho_2)}^3\\ \hline
\rho_3 & {(\rho_2)}^2 & {(\rho_2)}^3 & \rho_2
\end{array}
$$

　$${3\times3=9}$$ 通りのすべての結果は $${\rho_2}$$ のみで表されます。

巡回群を図形的にイメージ

　ここで、巡回群を図形的にイメージしましょう。
　３次対称群 $${N=\{id,  \rho_2,  \rho_3\}}$$ の要素は、三角形の回転でイメージすることができます（本シリーズ (14), (28)）。

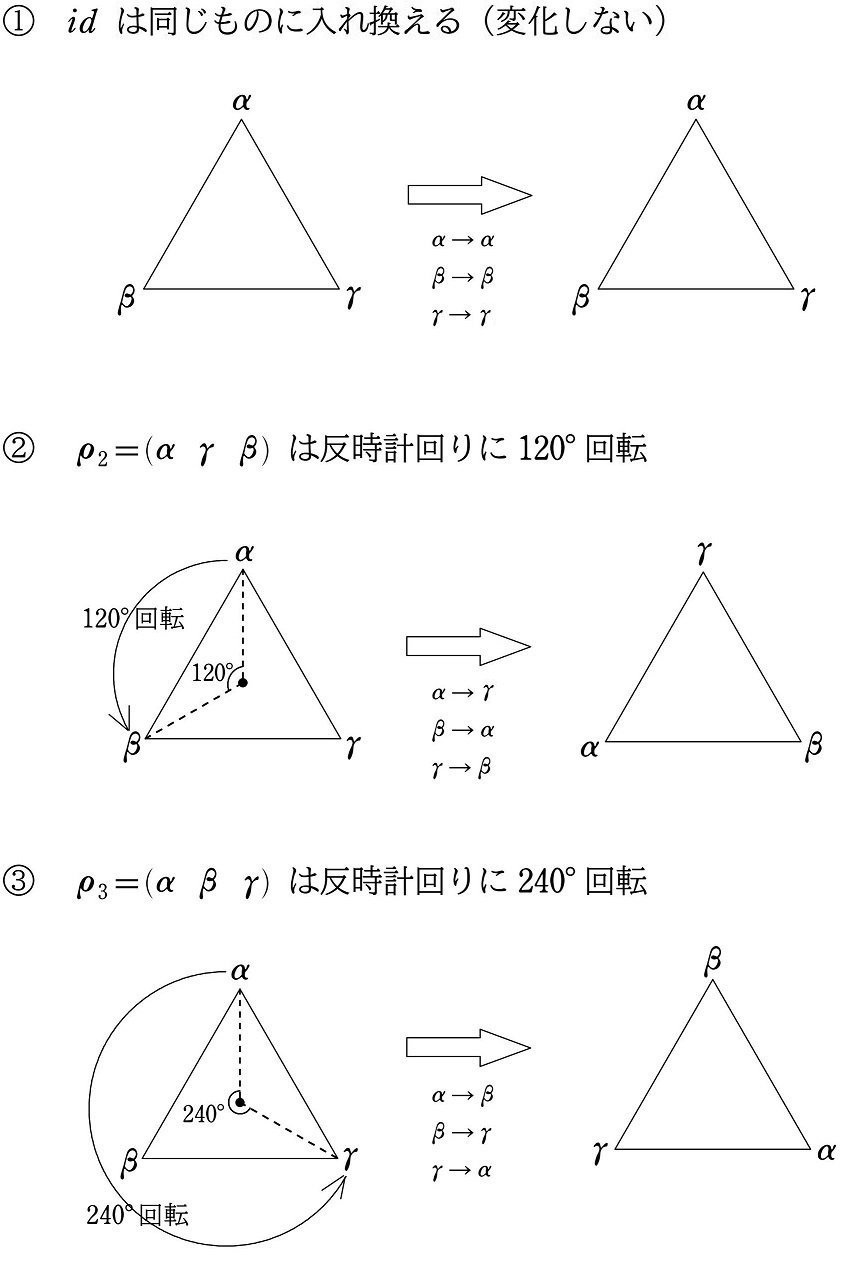
　$${id}$$ は何も回転しない、つまり $${0\degree}$$ 回転とみなします$${（➀）}$$。
　$${\rho_2}$$ は $${120\degree}$$ 回転とみなします$${（➁）}$$。
　$${\rho_3}$$ は $${240\degree}$$ 回転とみなします$${（➂）}$$。
　すると、$${120\degree}$$ 回転 $${(\rho_2)}$$ を３回繰り返すと $${360\degree}$$、つまり何も回転しない $${0\degree}$$ 回転 $${(id)}$$ と同じなので
　$${id={(\rho_2)}^3}$$
　また、$${120\degree}$$ 回転 $${(\rho_2)}$$ を２回繰り返すと $${240\degree}$$ 回転 $${(\rho_3)}$$ と同じなので
　$${\rho_3={(\rho_2)}^2}$$
　つまり、$${0\degree}$$ 回転 $${(id)}$$ と $${240\degree}$$ 回転 $${(\rho_3)}$$ は、$${120\degree}$$ 回転 $${(\rho_2)}$$ １つだけで表すことができます。

３次対称群は巡回群ではないこと

　なお、３次対称群 $${S_3=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}}$$ は巡回群ではありません。先ほどみたように、$${S_3}$$ の要素のうち $${id}$$ と $${\rho_3}$$ は
　$${id=(\rho_2)^3}$$
　$${\rho_3=(\rho_2)^2}$$
と、ひとつの要素 $${\rho_2}$$ だけを用いて表すことができますが、$${\tau_1,  \tau_2,  \tau_3}$$ は $${\rho_2}$$ だけを用いて表すことはできません。
　その理由を図形的に解説すると、$${\tau_1,  \tau_2,  \tau_3}$$ は反転を意味することはすでにやりました（本シリーズ (28)）。

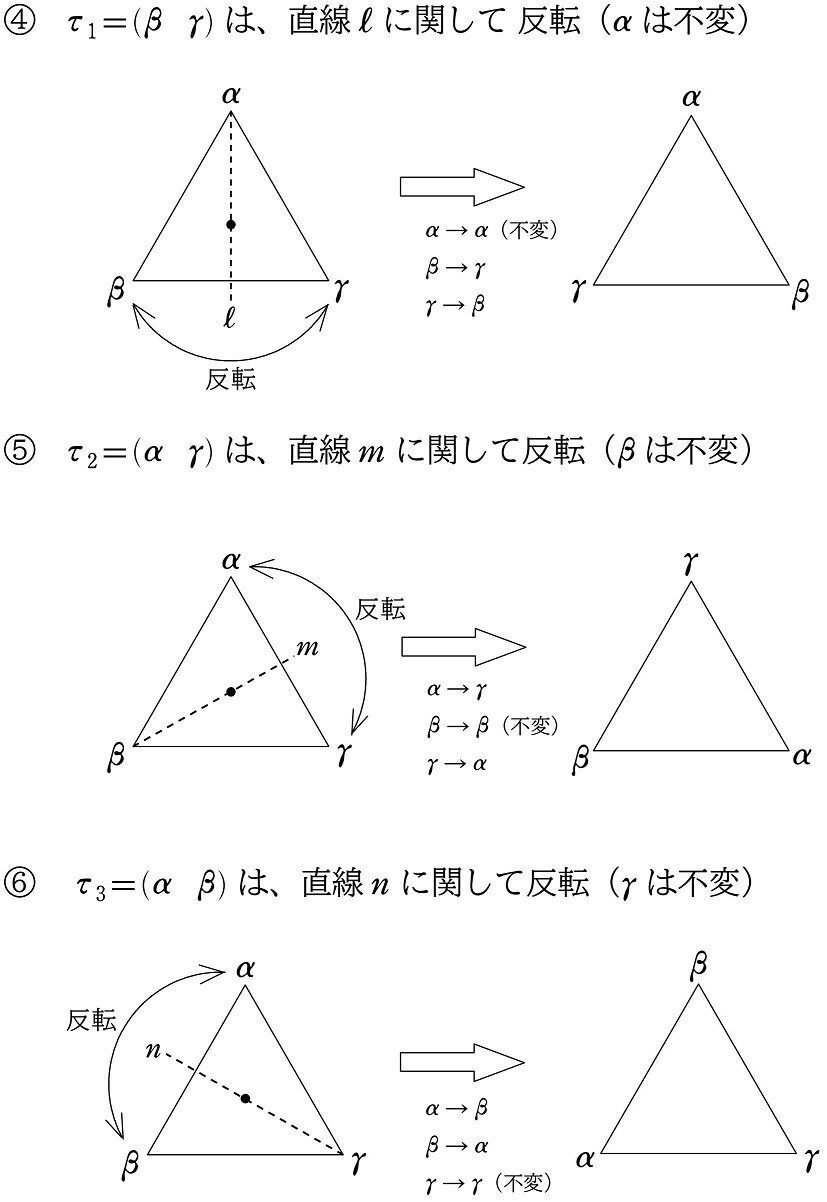
　この反転は、$${180\degree}$$ 回転ととらえることができます。

　すると、これらの $${180\degree}$$ 回転 $${(\tau_1,  \tau_2,  \tau_3)}$$ は、$${120\degree}$$ 回転 $${(\rho_2)}$$ だけで表すことはできません。$${120\degree}$$ 単位で何度回しても、$${180\degree}$$ ちょうどにはならないからです。それが $${\tau_1,  \tau_2,  \tau_3}$$ を $${\rho_2}$$ だけを用いて表すことのできない図形的イメージです。

N による左剰余類の集合が巡回群になること

　ここで、$${S_3}$$ の正規部分群 $${N=\{id,  \rho_2,  \rho_3\}}$$ による左剰余類の集合
　$${\{idN,  \tau_1N\}}$$
を考えてみましょう。本シリーズ (32) でやった「正規部分群の縮小」の流れ図

$$
\begin{align*}
S_3&=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}  は群\\[10pt]
縮小  &\downarrow  {\small 正規部分群  N=\{id,  \rho_2,  \rho_3\}  による \atop \hspace{-19pt}剰余群  \underline{\{idN,  \tau_1N\}}  が構成可能}\\[12pt]
N&=\{id,  \rho_2,  \rho_3\}\\[10pt]
縮小  &\downarrow  {\small \hspace{-26pt}正規部分群  I=\{id\}  による \atop 剰余群  \{idI,  \rho_2I,  \rho_3I\}  が構成可能}\\[12pt]
I&=\{id\}
\end{align*}
$$

の下線部の集合です。
　この集合が群（剰余群）になることは、本シリーズ (31)ですでに解説しましたが、実は巡回群にもなっています。

　その理由は、$${\{idN,  \tau_1N\}}$$ の要素同士について、その積の演算表（本シリーズ (31)）

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & idN & \underline{\tau_1N}\\ \hline\hline
idN & idN & \tau_1N\\ \hline
\underline{\tau_1N} & \tau_1N & \underline{idN}
\end{array}
$$

より
　$${\tau_1N\tau_1N=idN}$$（下線部）
つまり
　$${(\tau_1N)^2=idN}$$
なので

$$
\begin{align*}
\{idN,  \tau_1N\}&=\{(\tau_1N)^2,  \tau_1N\}\\
&=\{\tau_1N,  (\tau_1N)^2\}
\end{align*}
$$

　これで、ひとつの要素 $${\tau_1N}$$ だけを用いて表すことができたので、この剰余群は巡回群です。生成元は $${\tau_1N}$$ なので、次のように表せます。

$$
\begin{align*}
\{idN,  \tau_1N\}&=\{\tau_1N,  (\tau_1N)^2\}\\
&=\langle\tau_1N\rangle
\end{align*}
$$

　この巡回群 $${\{idN,  \tau_1N\}}$$ は、$${\tau_1N}$$ に次々と $${\tau_1N}$$ を作用させていけば、その要素は巡回的にすべて現れます。

$$
\begin{align*}
&\tau_1N\\
&\downarrow  {\small \tau_1N を作用}\\
\tau_1N\tau_1N=\;&idN\\
&\downarrow  {\small \tau_1N を作用}\\
idN\tau_1N=\;&\tau_1N\\
&\downarrow  {\small \tau_1N を作用}\\
\tau_1N\tau_1N=\;&idN\\
&\downarrow    {\small 以下繰り返し}\\
&\hspace{4pt}\vdots
\end{align*}
$$

　つまり

　円で描くと

　ちなみに、$${\{idN,  \tau_1N\}}$$ の要素同士の積の演算表

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & idN & \tau_1N\\ \hline\hline
idN & idN & \tau_1N\\ \hline
\tau_1N & \tau_1N & idN
\end{array}
$$

を、生成元 $${\tau_1N}$$ だけで表すと次のようになります。

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & idN & \tau_1N\\ \hline\hline
idN & (\tau_1N)^2 & \tau_1N\\ \hline
\tau_1N & \tau_1N & (\tau_1N)^2
\end{array}
$$

　$${2\times2=4}$$ 通りのすべての結果は $${\tau_1N}$$ のみで表されます。
　なお、同様の議論によって、$${S_3}$$ の正規部分群 $${N}$$ による右剰余類の集合
　$${\{Nid,  N\tau_1\}}$$
も巡回群になります。

I による左剰余類の集合が巡回群になること

　次に、３次交代群 $${N=\{id,  \rho_2,  \rho_3\}}$$ の正規部分群
　$${I=\{id\}}$$
による左剰余類の集合
　$${\{idI,  \rho_2I,  \rho_3I\}}$$
を考えてみましょう。本シリーズ (32) でやった「正規部分群の縮小」の流れ図

$$
\begin{align*}
S_3&=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}  は群\\[10pt]
縮小  &\downarrow  {\small 正規部分群  N=\{id,  \rho_2,  \rho_3\}  による \atop \hspace{-19pt}剰余群  \{idN,  \tau_1N\}  が構成可能}\\[12pt]
N&=\{id,  \rho_2,  \rho_3\}\\[10pt]
縮小  &\downarrow  {\small \hspace{-26pt}正規部分群  I=\{id\}  による \atop 剰余群  \underline{\{idI,  \rho_2I,  \rho_3I\}}  が構成可能}\\[12pt]
I&=\{id\}
\end{align*}
$$

の下線部の集合です。
　この集合が群（剰余群）になることは、すでに本シリーズ (32) で解説しましたが、実は巡回群にもなっています。

　その理由は、$${\{idI,  \rho_2I,  \rho_3I\}}$$ の要素同士について、その積の演算表

$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & idI & \utilde{\underline{\rho_2I}} & \rho_3I\\ \hline\hline
idI & idI & \rho_2I & \rho_3I\\ \hline
\underline{\rho_2I} & \rho_2I & \underline{\rho_3I} & idI\\ \hline
\utilde{\rho_3I} & \rho_3I & \utilde{idI} & \rho_2I
\end{array}
$$

より

　$${\rho_2I\rho_2I=\underline{\rho_3I}　\cdots (*1)}$$（下線部）
　$${\rho_3I\rho_2I=\utilde{idI}　\cdots (*2)}$$（斜線部）

　同じものの置換の積を
　$${\rho_2I\rho_2I={(\rho_2I)}^2　\cdots (*3)}$$
　$${\rho_2I\rho_2I\rho_2I={(\rho_2I)}^3　\cdots (*4)}$$
$${\hspace{45pt}\vdots}$$
と表せるので

$$
\begin{alignat*}{2}
idI&=\rho_3I\rho_2I &　&{\small (*2) より}\\
&=(\rho_2I\rho_2I)\rho_2I &　&{\small (*1) より}\\
&=\rho_2I\rho_2I\rho_2I &　&{\small 結合法則より}\\
&={(\rho_2I)}^3 &　&{\small (*4) より}\\[10pt]
\rho_3I&=\rho_2I\rho_2I &　&{\small (*1) より}\\
&={(\rho_2I)}^2 &　&{\small (*3) より}
\end{alignat*}
$$

より

$$
\begin{align*}
idI&={(\rho_2I)}^3\\
\rho_3I&={(\rho_2I)}^2
\end{align*}
$$

よって

$$
\begin{align*}
\{idI,  \rho_2I,  \rho_3I\}&=\{{(\rho_2I)}^3,  \rho_2I,  {(\rho_2I)}^2\}\\
&=\{\rho_2I,  {(\rho_2I)}^2,  {(\rho_2I)}^3\}
\end{align*}
$$

　これで、ひとつの要素 $${\rho_2I}$$ だけを用いて表すことができたので、この剰余群は巡回群です。生成元は $${\rho_2I}$$ なので、次のように表せます。

$$
\begin{align*}
\{idI,  \rho_2I,  \rho_3I\}&=\{\rho_2I,  {(\rho_2I)}^2,  {(\rho_2I)}^3\}\\
&=\langle\rho_2I\rangle
\end{align*}
$$

　この巡回群 $${\{idI,  \rho_2I,  \rho_3I\}}$$ は、$${\rho_2I}$$ に次々と $${\rho_2I}$$ を作用させていけば、その要素は巡回的にすべて現れます。

$$
\begin{align*}
&\rho_2I\\
&\downarrow  {\small \rho_2I を作用}\\
\rho_2I\rho_2I=&\rho_3I\\
&\downarrow  {\small \rho_2I を作用}\\
\rho_3I\rho_2I=&idI\\
&\downarrow  {\small \rho_2I を作用}\\
id\rho_2I=&\rho_2I\\
&\downarrow  {\small 以下繰り返し}\\
&\hspace{4pt}\vdots
\end{align*}
$$

　つまり

　円で描くと

　ちなみに、$${\{idI,  \rho_2I,  \rho_3I\}}$$ の要素同士の積の演算表

$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & idI & \rho_2I & \rho_3I\\ \hline\hline
idI & idI & \rho_2I & \rho_3I\\ \hline
\rho_2I & \rho_2I & \rho_3I & idI\\ \hline
\rho_3I & \rho_3I & idI & \rho_2I
\end{array}
$$

を、生成元 $${\rho_2I}$$ だけで表すと次のようになります。

$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & idI & \rho_2I & \rho_3I\\ \hline\hline
idI & {(\rho_2I)}^3 & \rho_2I & {(\rho_2I)}^2\\ \hline
\rho_2I & \rho_2I & {(\rho_2I)}^2 & {(\rho_2I)}^3\\ \hline
\rho_3I & {(\rho_2I)}^2 & {(\rho_2I)}^3 & \rho_2I
\end{array}
$$

　$${3\times3=9}$$ 通りのすべての結果は $${\rho_2I}$$ のみで表されます。
　なお、同様の議論によって、$${N}$$ の正規部分群 $${I=\{id\}}$$ による右剰余類の集合
　$${\{Iid,  I\rho_2,  I\rho_3\}}$$
も巡回群になります。

まとめ

$${➀}$$　巡回群とは「すべての要素が、あるひとつの要素だけを用いて表すことのできる群」です。

$${➁}$$　３次対称群 $${S_3=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}}$$ は巡回群ではありません。

$${➂}$$　３次対称群 $${S_3}$$ の正規部分群である３次交代群 $${N=\{id,  \rho_2,  \rho_3\}}$$ は巡回群です。つまり

$$
\begin{align*}
N&=\{id,  \rho_2,  \rho_3\}\\
&=\{\rho_2,  {(\rho_2)}^2,  {(\rho_2)}^3\}\\
&=\langle\rho_2\rangle
\end{align*}
$$

$${➃}$$　$${N}$$ による左剰余類の集合 $${\{idN,  \tau_1N\}}$$ は巡回群です。つまり

$$
\begin{align*}
\{idN,  \tau_1N\}&=\{\tau_1N,  (\tau_1N)^2\}\\
&=\langle\tau_1N\rangle
\end{align*}
$$

$${➄}$$　３次交代群 $${N=\{id,  \rho_2,  \rho_3\}}$$ の正規部分群 $${I=\{id\}}$$ について、$${I}$$ による左剰余類の集合 $${\{idI,  \rho_2I,  \rho_3I\}}$$ は巡回群です。つまり

$$
\begin{align*}
\{idI,  \rho_2I,  \rho_3I\}&=\{\rho_2I,  {(\rho_2I)}^2,  {(\rho_2I)}^3\}\\
&=\langle\rho_2I\rangle
\end{align*}
$$

　復習として、本シリーズ (32) でやった「正規部分群の縮小」の流れ図

$$
\begin{align*}
S_3&=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}  は群\\[10pt]
縮小  &\downarrow  {\small 正規部分群  N=\{id,  \rho_2,  \rho_3\}  による \atop \hspace{-19pt}剰余群  \{idN,  \tau_1N\}  が構成可能}\\[12pt]
N&=\{id,  \rho_2,  \rho_3\}\\[10pt]
縮小  &\downarrow  {\small \hspace{-26pt}正規部分群  I=\{id\}  による \atop 剰余群  \{idI,  \rho_2I,  \rho_3I\}  が構成可能}\\[12pt]
I&=\{id\}
\end{align*}
$$

を用いて整理すると、本記事で述べたことは次の黒字部分です。

$$
\begin{align*}
S_3&=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}  は\bm{巡回群ではない}\\[10pt]
縮小  &\downarrow  {\small \hspace{-15pt}正規部分群 N=\{id,  \rho_2,  \rho_3\} による \atop \hspace{0pt}\bm{巡回群}  \{idN,  \tau_1N\}=\langle\tau_1N\rangle  が構成可能}\\[12pt]
N&=\{id,  \rho_2,  \rho_3\}=\langle\rho_2\rangle  は\bm{巡回群}\\[10pt]
縮小  &\downarrow  {\small \hspace{-58pt}正規部分群  I=\{id\}  による \atop \bm{巡回群}  \{idI,  \rho_2I,  \rho_3I\}=\langle\rho_2I\rangle  が構成可能}\\[12pt]
I&=\{id\}
\end{align*}
$$

　なお、$${N}$$ が巡回群であることは本質的ではなく、$${S_3}$$ の正規部分群であることが重要です。$${I}$$ も $${N}$$ の正規部分群であり、群の縮小の列は、「その前の群の正規部分群」になっていることが、解の公式が存在するかどうかを判定する上で重要になります。

$$
\begin{align*}
S_3\hspace{4pt}\overset{縮小}{\supset}\hspace{-8pt}\underset{\tiny S_3 の正規部分群}{N}\hspace{-8pt}\overset{縮小}{\supset}\hspace{-8pt}\underset{\tiny N の正規部分群}{I}
\end{align*}
$$

　つまり、次の黒字部分が重要になります。

$$
\begin{align*}
S_3&=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}  は\bm{群}\\[10pt]
\bm{縮小}  &\downarrow  {\small \hspace{-15pt}正規部分群  N=\{id,  \rho_2,  \rho_3\}  による \atop \hspace{0pt}\bm{巡回群}  \{idN,  \tau_1N\}=\langle\tau_1N\rangle  が構成可能}\\[12pt]
N&=\{id,  \rho_2,  \rho_3\}  は  S_3  の\bm{正規部分群}\\[10pt]
\bm{縮小}  &\downarrow  {\small \hspace{-58pt}正規部分群  I=\{id\}  による \atop \bm{巡回群}  \{idI,  \rho_2I,  \rho_3I\}=\langle\rho_2I\rangle  が構成可能}\\[12pt]
I&=\{id\}  は  N  の\bm{正規部分群}
\end{align*}
$$

　まとめると、
　$${➀}$$ 正規部分群を取りながら群が縮小すること
　$${➁}$$ その正規部分群による剰余類の集合が巡回群になること
の２つの関係を保持しながら、単位元のみからなる正規部分群 $${\{id\}}$$ にうまくたどり着くことができれば、その方程式には解の公式が存在する。逆に $${\{id\}}$$ にたどり着かなければ、解の公式は存在しない、というのがガロアのアイデアです。

（参考）各章の内容

（１）「２次方程式の解の公式」を式変形で導出
　　　・平方完成
（２）「３次方程式の解の公式」を導出するための準備
　　　・$${1}$$ の３乗根 $${\omega}$$
（３）「３次方程式の解の公式」を式変形で導出
　　　・チルンハウス変換
（４）「解と係数の関係」と「対称式」の解説
（５）「対称式」を用いた「２次方程式の解の公式」の導出
（６）「解の置換」と「ラグランジュ・リゾルベント」の解説
（７）「ラグランジュ・リゾルベント」による「３次方程式の解の公式」の導出
（８）「遇置換」と「奇置換」の解説（ここから「アーベルの証明」の準備）
（９）「差積の２乗」が対称式となること、及び「差積」と平方根を結ぶ等式の証明。
（10）「平方根」「３乗根」と次々と累乗根を加えていくアイデア
（11）「アーベルの証明」のアイデアを用いて、なぜ「２次方程式の解の公式が存在するのか」を解説（添加する式について加筆予定）
（12）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（前編）。「差積の２乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む（対称性の破壊）。
（13）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（後編）。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む（対称性の破壊）。$${\longrightarrow}$$ ３次方程式の解の公式の完成
（14）「アーベルの証明」の解説①。５次方程式の解の差積（または差積の２乗の平方根）を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が５次置換（対称式）から遇置換シンメトリーへと破壊されることを解説。
（15）「アーベルの証明」の解説②。すべての置換は互換で表せることから、５次置換をすべて互換の積で表して、遇置換と奇置換に分類する。
（16）「アーベルの証明」の解説➂。「すべての遇置換は３次巡回置換の積で表される」ことの解説。
（17）「アーベルの証明」の解説➃（最後）。「任意の３次巡回置換が５次巡回置換の積で表せる」ことによって、５次方程式には解の公式が存在しないことが証明されることの解説。
（18）もっと分かりやすくシリーズ①「累乗根の添加」について重点解説。
（19）もっと分かりやすくシリーズ②「対称性の破壊」について重点解説。
（20）もっと分かりやすくシリーズ③「対称性を恒等置換まで破壊」することについて重点解説。
（21）もっと分かりやすくシリーズ➃　何次方程式でも「最初に解の差積を添加して対称性を破壊すること」は常套手段。
（22）もっと分かりやすくシリーズ➄「解の和と差の連立」による２次方程式の解の公式の導出について。
（23）もっと分かりやすくシリーズ➅「対称式ではない解の公式を基本対称式で表す」ことのついて。
（24）もっと分かりやすくシリーズ➆「定数 $${\bm{\omega}}$$」について復習
（25）もっと分かりやすくシリーズ➇　３次方程式の解の公式の導出方法「カルダノの方法」を復習
（26）もっと分かりやすくシリーズ➈「カルダノの方法」と「対称性の破壊」の関連について
（27）もっと分かりやすくシリーズ⑩　そもそもなぜ解の公式が存在しないかを『巡回置換』から紐解く
（28）中学でも分かるガロアの証明①　ガロアの発見した「群」について
（29）中学でも分かるガロアの証明②　ガロアの発見した「部分群」について
（30）中学でも分かるガロアの証明③　ガロアの発見した「正規部分群」について
（31）中学でも分かるガロアの証明④　正規部分群による剰余類の集合が群（剰余群）になること
（32）中学でも分かるガロアの証明④　単位元のみの正規部分群 $${\{id\}}$$ による剰余類の集合が群（剰余群）になること