
第7章「SNSではどのような自分語りが許されるのか?」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング2」の第7章「SNSではどのような自分語りが許されるのか?」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
この章では、Twitter(現 X)とFacebookで行われる自分語りの適切さ評価に取り組みます。
SNSで自分のことをどのくらい、どんな内容を投稿するのが適切/不適切なのかを推論します。
3つの評価テーマごとに3つのベイズモデルを構築します。

今回のPyMCモデリングは「2勝1敗」で勝ち越しました(何に勝った?)。
3つのモデルはベイズ統計モデリングの基礎体力づくりに適切なものばかり。
ぜひぜひ、PyMCのベイズモデリングの世界を楽しみましょう。
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 松木祐馬 先生
モデル難易度: ★★・・・ (やさしめ)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★★・・ & そこそこ \\
結果再現度 & ★★★・・ & そこそこ \\
楽しさ & ★★★★★ & 楽しい! \\
\end{array}
$$

評価ポイント
自己評価に悩みました。
3つのモデルのうち、1番目と3番目は比較的シンプルなモデルであり、テキストとほぼ同じ結果を導くことができました。
この2つだけで評価すると満点に近いと思います。しかし2番目のモデルを加えると、評価が落ちてしまいます。
モデル自体はそれほど難しくないのですが、PyMC実装方法を見つけられなかったただ1点が・・・。
「2次元配列の変数」に対して「1次元目の合計が0」かつ「2次元目の合計が0」の制約(注)を設定することができませんでした。
(注)
PyMCのtransforms.ZeroSumTransformによる合計0制約は、1次元目のみの0制約、2次元目のみの0制約、1次元目と2次元目の要素をすべて合わせて合計0にする制約はできるようですが、「1次元目だけの合計が0」かつ「2次元目だけの合計が0」の制約はできなさそうです。
工夫・喜び・反省
R・Stanのサンプルコードはシンプルな代入関係・簡単なfor文・ひと目で分かりやすい関数を積極的に利用しています。そして、適度のコメント文が添えられています。
「読み手」にとって「とても理解しやすいコードの書き方」です。
真似したいと思います!

モデルの概要
テキストの調査・実験の概要
■ 調査の概要
大学生・専門学生 234名から回答を得て、TwitterとFacebookの両方の利用経験がある198名の回答を分析するとしています。
■ 質問項目の概要
TwitterとFacebook上で行う「自己開示の適切さ」と「発言に関する個人の態度」1~5点で回答を得ます。
点はおそらく、0:全く当てはまらない~5:とても当てはまる、のような感じだと思われます。
質問項目について、テキストの掲載内容を引用いたします。

テキストのモデリング
テキストでは、3つの分析テーマごとにベイズモデルを構築しています。
1.発言に関する個人の態度の分析~参加者内1要因モデル
このモデルを用いて、「発言に関する個人の態度」の「発言のしやすさ」、「発言に対する軽率さ」、「他者反応への注意」に関するSNS種類ごとの得点平均を推論し、TwitterとFacebookの比較をします。
目的変数のざっくり数式です。

■目的変数と関心のあるパラメータ
目的変数はSNSの種類$${j}$$ごとの参加者$${l}$$の「発言に関する個人の態度」の得点(回答)$${y_jl}$$です。
関心のあるパラメータは「発言に関する個人の態度」の3分類ごとのSNS種類別の得点平均$${\mu_j}$$です。
添字$${j}$$はSNSの種類であり、1:Twitter、2:Facebookです。
$${l}$$は参加者のIDです。
参加者内1要因モデルは次のとおりです。
$$
\begin{align*}
y_{jl} &= \mu_j + s_l + e_{jl} \\
s_l &\sim \text{Normal}\ (0,\ \sigma_s) \\
e_{jl} &\sim \text{Noemal}\ (0,\ \sigma_e) \\
\end{align*}
$$
$${\mu_j}$$は各SNSの平均、$${s_l}$$は参加者の効果です。
ベイズモデルに転換すると次のようになります。
$$
\begin{align*}
y_{jl} &\sim \text{Normal}\ (\mu_j+s_l,\ \sigma_e) \\
s_l &\sim \text{Normal}\ (0,\ \sigma_s) \\
\end{align*}
$$
$${\mu_j,\ \sigma_s,\ \sigma_e}$$の事前分布は十分に範囲の広い適当な一様分布です。
なお、このモデルのPyMC化は収束し、テキストとほぼ同じ結果を得ています。

2.自己開示の適切さの分析~参加者内2要因モデル
このモデルを用いて、「自己開示の適切さ」の「日常的開示」、「目標・関心事の開示」、「ネガティブな開示」、「周囲の他者の開示」に関するSNS種類ごとの得点平均等の多くのパラメータを推論し、TwitterとFacebookの比較をします。
目的変数のざっくり数式です。

■目的変数と関心のあるパラメータ
目的変数はSNSの種類$${j}$$ごとの参加者$${l}$$の「自己開示の適切さ」の得点(回答)$${y_ikl}$$です。
関心のあるパラメータは「自己開示の適切さ」の4分類ごとのSNS種類別の得点平均$${\mu_j}$$、SNSの種類の効果$${a_j}$$、開示内容の効果$${b_k}$$など、様々なパラメータです。
添字$${j}$$はSNSの種類であり、1:Twitter、2:Facebookです。
$${l}$$は参加者のIDです。
$${k}$$は「自己開示の適切さ」の開示内容4項目です。
参加者内2要因モデルは次のとおりです。
$$
\begin{align*}
y_{jkl} &= \mu + a_j + b_k + s_l + (ab)_{jk} + (as)_{jl} + (bs)_{kl}+ e_{jkl} \\
s_l &\sim \text{Normal}\ (0,\ \sigma_s) \\
(as)_{jl} &\sim \text{Normal}\ (0,\ \sigma_{as}) \\
(bs)_{kl} &\sim \text{Normal}\ (0,\ \sigma_{bs}) \\
e_{jkl} &\sim \text{Noemal}\ (0,\ \sigma_e) \\
\displaystyle \sum^a_{j=1} a_j &= 0 \\
\displaystyle \sum^b_{k=1} a_j &= 0 \\
\displaystyle \sum^a_{j=1} (ab)_{jk} &= 0 \\
\displaystyle \sum^b_{k=1} (ab)_{jk} &= 0 \\
\end{align*}
$$
$${\mu}$$は全平均、$${a_j}$$はSNSの種類の効果、$${b_k}$$は開示内容の効果、$${s_l}$$は参加者の効果、$${(ab)_{jk}}$$はSNSの種類と開示内容の交互作用、$${(as)_{jl}}$$はSNSの種類と参加者の交互作用、$${(bs)_{kl}}$$は開示内容と参加者の交互作用です。
最後の4行はパラメータ値の合計が0にする制約式です。
特に、$${\sum^a_{j=1} (ab)_{jk} = 0}$$と$${\sum^b_{k=1} (ab)_{jk} = 0}$$は、自己流PyMCモデリング時に波乱の種になります。。。
ベイズモデルの転換内容は省略いたします。
PyMCのモデル数式をご覧ください。
なお、このモデルのPyMC化は収束できませんでした。

3.発言に関する個人の態度と自己開示の適切さとの関連の分析~階層線形モデル
このモデルを用いて、線形モデルの標準偏回帰係数を「SNSの種類」別・「発言に関する個人の態度」別・「自己開示の適切さ」別に推論し、TwitterとFacebookの比較をします。
目的変数のざっくり数式です。

■目的変数と関心のあるパラメータ
目的変数は「発言に関する個人の態度」$${i}$$・SNSの種類$${j}$$・参加者$${l}$$ごとの「発言に関する個人の態度」の得点(回答)$${y_ijl}$$です。
関心のあるパラメータは「自己開示の適切さ」をベースにした標準偏回帰係数$${\beta_{j1},\beta_{j2},\beta_{j3}}$$です(添字に無いですが「発言に関する個人の態度4つ」の切り口を含みます)。
添字$${j}$$はSNSの種類であり、1:Twitter、2:Facebookです。
$${l}$$は参加者者のIDです。
$${i}$$はテキストに明示されていませんが「発言に関する個人の態度」の4つと思われます。
階層線形モデルは次のとおりです。
$$
\begin{align*}
y_{ijl} &= a_j + \beta_{j1}x_{ij1} + \beta_{j2}x_{ij2}+ \beta_{j3}x_{ij3} + s_l + e_{jl} \\
&(j=1, 2, \quad l=1, \cdots, 198) \\
s_l &\sim \text{Normal}\ (0,\ \sigma_s) \\
e_{ijl} &\sim \text{Noemal}\ (0,\ \sigma_e) \\
\end{align*}
$$
$${a_j}$$は切片、$${x_1}$$は発言のしやすさ、$${x2}$$は発言に対する軽率さ、$${x3}$$は他者反応への注意の得点、$${\beta_{j1}, \beta_{j2}, \beta_{j3}}$$は偏回帰係数、$${s_l}$$は参加者の効果です。
ベイズモデルの転換内容は省略いたします。
PyMCのモデル数式をご覧ください。
なお、このモデルのPyMC化は収束し、テキストとほぼ同じ結果を得ています。
■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCの自己流モデルには、分析に利用可能なモデルとそうでないモデルがありますのでご注意くださいませ。

PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.インポート
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')2.データの読み込み(その1)
サンプルコードに含まれるデータは2つあります。
こちらでは「snsdata.csv」をpandasのデータフレームに読み込みます。
### データの読み込み
# 列名の設定
col_names = ['SNS', 'ID', '日常的開示', '目的・関心事の開示', 'ネガティブな開示',
'周囲の他者の開示', '発言のしやすさ', '発言に対する軽率さ',
'他者反応への注意']
# csvファイルの読み込み
data1 = pd.read_csv('snsdata.csv', skiprows=1, names=col_names)
# データフレームの表示
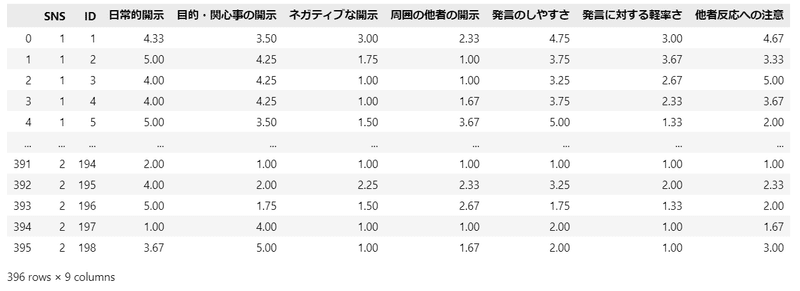
display(data1.round(2))【実行結果】
396行のデータです。
列の内容は次のとおりです。
・SNS:SNSの種類(1:Twitter、2:Facebook)
・ID:参加者のID(1から198)
・日常的開示~他者反応への注意:参加者が回答した得点
SNSの種類別に要約統計量を見てみましょう。
Twitterから。
### SNS別の要約統計量の表示 Twitter
data1[data1['SNS']==1].describe().round(1)【実行結果】

続いてFacebook.
### SNS別の要約統計量の表示 Facebook
data1[data1['SNS']==2].describe().round(1)【実行結果】

「発言のしやすさ」の違いが際立っています。
Twitterの平均値は3.8、Facebookは2.8。
可視化して比較しましょう。箱ひげ図で2つのSNSを比べます。
seaborn の boxplot を利用します。
### 尺度別・SNS別の箱ひげ図の描画
# snsのlist
sns_list = ['Twitter', 'Facebook']
# 尺度のlist
measure_list = data1.columns[2:].values.tolist()
## データ前処理
# seabornで利用しやすい縦持ちに変換
tmp = data1.melt(id_vars=['SNS', 'ID'], value_vars=measure_list,
var_name='尺度', value_name='得点')
# SNS名称をセット
tmp['SNS'] = tmp['SNS'].apply(lambda x: sns_list[x-1])
## 描画
plt.figure(figsize=(10, 4))
# 箱ひげ図の描画
sns.boxplot(data=tmp, x='尺度', y='得点', hue='SNS', palette='Set3', gap=0.1)
# 修飾 x軸目盛ラベルの回転、凡例をグラフの外に横並び形式で表示
plt.xticks(rotation=10);
plt.legend(ncols=2, bbox_to_anchor=(0, 1), loc='lower left');【実行結果】
日常的開示と目的・関心事の開示は2つのSNSともに「適切」サイドに寄っていて、ネガティブな開示と周囲の他者の開示は2つのSNSともに「不適切」サイドに寄っています。
尺度(横軸)ごとに2つのSNSを比べると微妙な差が見られます。
SNS利用の特徴が現れているのかもしれません。


モデル1の構築「参加者内1要因モデル」
テキストでは「発言に関する個人の態度」3項目のモデルとしていますが、
ここでは「自己開示の適切さ」4項目と「発言に関する個人の態度」3項目の計7項目を対象にして、モデル構築+推論を行います。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
$$
\begin{align*}
\sigma_s &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100)\\
\sigma_e &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100)\\
\mu &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100,\ \text{dims}=sns)\\
s &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_s,\ \text{dims}=id) \\
likelihood &\sim \text{Normal}\ (\text{mu}=\mu[snsIdx] + s[idIdx],\ \text{sigma}=\sigma_e) \\
\end{align*}
$$
1.モデルの定義
7項目の推論を一気に行う目的で、モデル定義関数を定義して、MCMCをまとめて実施しします。
数式表現を実直にモデル記述します。
### モデル定義関数の定義
def make_model(df, data):
# モデルの定義
with pm.Model() as model:
### データ関連定義
# coordの定義
model.add_coord('data', values=df.index, mutable=True)
model.add_coord('sns', values=sns_list, mutable=True)
model.add_coord('id', values=list(range(1, df['ID'].max()+1)),
mutable=True)
# dataの定義
y = pm.ConstantData('y', value=data.values, dims='data')
snsIdx = pm.ConstantData('snsIdx', value=df['SNS'].values - 1,
dims='data')
idIdx = pm.ConstantData('idIdx', value=df['ID'].values - 1,
dims='data')
### 事前分布
sigmaS = pm.Uniform('sigmaS', lower=0, upper=100)
sigmaE = pm.Uniform('sigmaE', lower=0, upper=100)
mu = pm.Uniform('mu', lower=0, upper=100, dims='sns')
s = pm.Normal('s', mu=0, sigma=sigmaS, dims='id')
### 尤度
likelihood = pm.Normal('likelihood', mu=mu[snsIdx]+s[idIdx],
sigma=sigmaE, observed=y, dims='data')
return model【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の3つを設定しました。データの行の座標:名前「data」、値「行インデックス」
SNSの座標:名前「sns」、値「'Twitter', 'Facebook'」
参加者IDの座標:名前「id」、値「1~198」
dataの定義
次の3つを設定しました。目的変数:得点 y
SNSインデックス snsIdx
参加者IDインデックス idIdx
パラメータの事前分布
$${\sigma_s, \sigma_e, \mu}$$は区間広めの一様分布を採用しました。
その他のパラメータはテキストの記載のとおりです。
尤度
観測値 y は「SNS別の平均$${\mu}$$+参加者の効果$${s}$$」を平均パラメータ、$${\sigma_e}$$を標準偏差パラメータにもつ正規分布に従います。
2.モデルの表示と事後分布からのサンプリング
7項目のモデルをまとめて処理します。
乱数生成数はテキストと同じです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ2分でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 2分
### MCMCの7つの尺度ごとにモデル定義・モデル表示・MCMCを実行
# 推論データを格納するリストの初期化
idata_list1 = []
# 尺度ごとに繰り返し処理
for i, col in enumerate(measure_list):
# モデルの定義(上のモデル定義関数の実行)
model1 = make_model(data1, data1[col])
# モデルの表示(1回目だけ)
if i == 0:
display(model1)
display(pm.model_to_graphviz(model1))
# MCMCの実行
# テキスト:iter=21000, warmup=1000, chains=5
with model1:
idata = pm.sample(draws=20000, tune=1000, chains=5, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1234)
# 推論データをリストに格納
idata_list1.append(idata) 【実行結果】
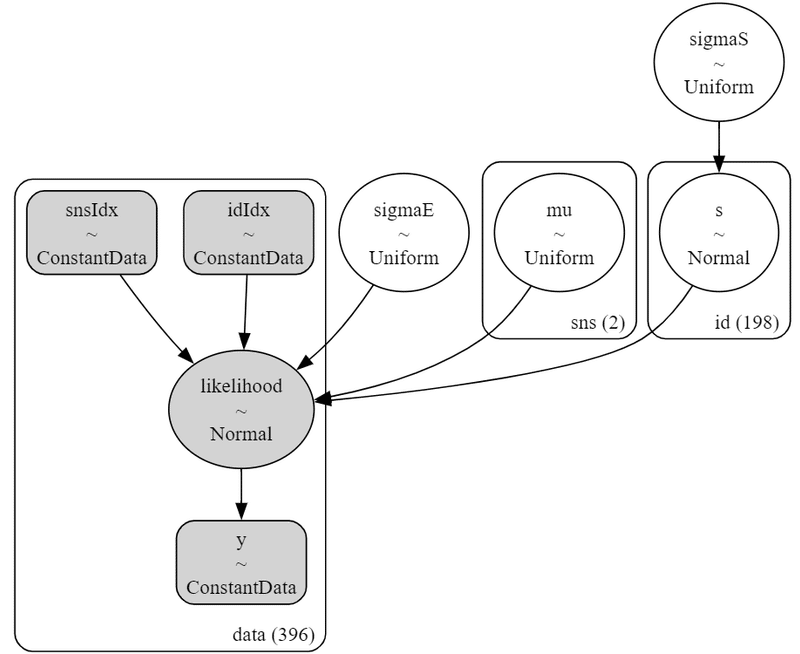
最初のモデルについて、数式と図を表示しました。
シンプルなモデルです。

MCMC実行時のプログレスバーです。
最初のモデルのものを掲載します。
実行時には残りの6モデルを含む全7つのプログレスバー群が表示されます。

4.サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$とします。
### r_hat>1.1の確認(しきい値は、テキスト:1.1、この処理:1.01) 1分
for i, idata in enumerate(idata_list1):
# 設定
idata_in = idata # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
print(f'{measure_list[i]}')
print((az.rhat(idata_in) > threshold).sum())【実行結果】
$${\hat{R} > 1.1}$$のパラメータはでカウントしたところ、0件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。



トレースプロットを確認しましょう。
### トレースプロットの表示 3分50秒
for i, idata in enumerate(idata_list1):
print(f'{measure_list[i]}')
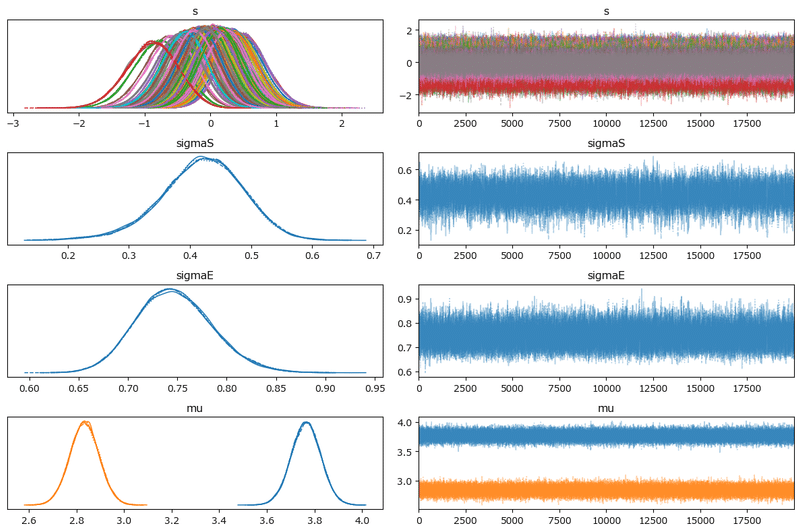
pm.plot_trace(idata, compact=True)
plt.tight_layout()
plt.show()【実行結果】
左のグラフから、5本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。

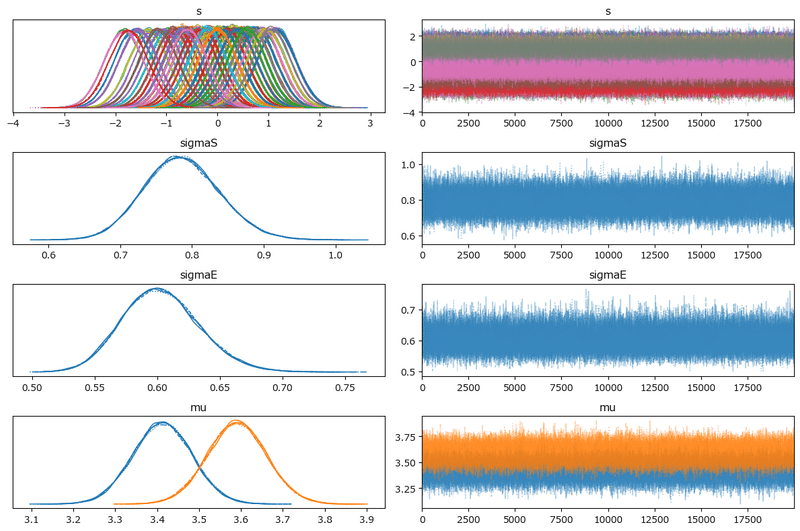
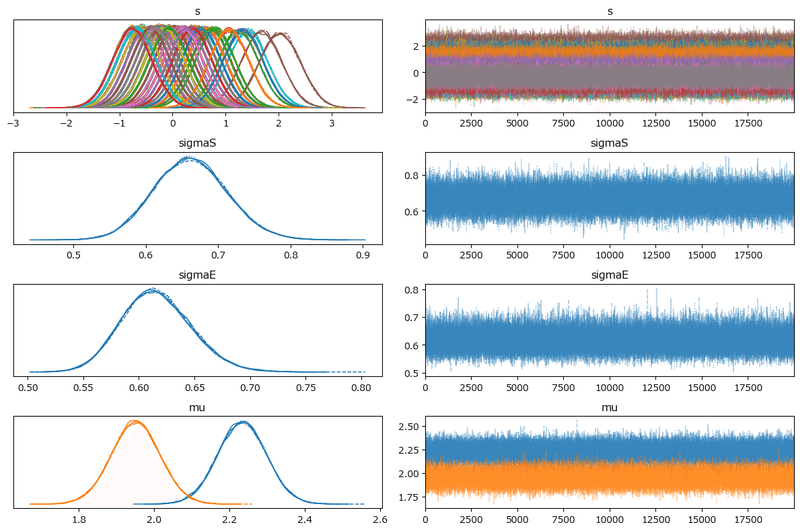


モデル1の分析「参加者内1要因モデル」
テキストにならって「発言に関する個人の態度」を分析します。
SNS別の得点の平均$${\mu}$$を分析します。
最初に事後分布の要約統計量を表示します。
テキストの表7.3に相当します
### 自己開示の適切さ尺度と発言に関する個人の態度尺度の事後統計量の表示
# ※表7.3に相当
## 統計量算出関数の定義
def calc_stats(x):
ci95 = np.quantile(x, q=[0.025, 0.975])
return [np.mean(x), np.std(x), ci95[0], np.median(x), ci95[1]]
## 尺度別・SNS別の事後統計量の算出
# 一時リストの初期化
tmp_list = []
# 尺度ごとに推論データを取り出して繰り返し処理
for i, idata in enumerate(idata_list1):
# 推論データを平坦化
tmp = idata.posterior.mu.stack(sample=('chain', 'draw')).data
# 2つのSNSごとに繰り返し処理
for j, snsname in enumerate(sns_list):
# 尺度名・SNS名・事後統計量を1つのリストに格納
tmp_data = [measure_list[i], snsname] + calc_stats(tmp[j])
# 一時リストに格納
tmp_list.append(tmp_data)
## データフレーム化
stats_df1 = pd.DataFrame(tmp_list,
columns=['尺度', 'SNS', 'EAP', 'post.sd', '2.5%CI',
'MED', '97.5%CI'])
display(stats_df1.round(2))【実行結果】
行番号8以降がテキストの分析対象です。
テキストの値とほぼ一致しました。

発言のしやすさ、発言にたいする軽率さ、他者反応への周囲のEAP(平均値)はすべてTwitterの方が値が大きいです。
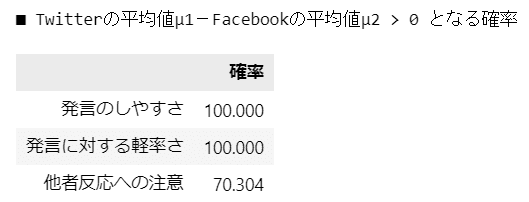
テキストにならって「Twitterの平均値とFacebookの平均値の差が0以上の確率」を算出しましょう。
### 発言に関する個人の態度の3尺度の平均値μについて、TwitterがFacebook超の確率
# テキスト本文75ページの確率に相当
# 推論データから発言のしやすさと発言の軽率さのデータを取り出し
shiyasusa = idata_list1[4].posterior.mu.stack(sample=('chain', 'draw')).data
keisotusa = idata_list1[5].posterior.mu.stack(sample=('chain', 'draw')).data
tashachui = idata_list1[6].posterior.mu.stack(sample=('chain', 'draw')).data
# TwitterとFacebookの比較
print('■ Twitterの平均値μ1-Facebookの平均値μ2 > 0 となる確率')
prob_df1 = pd.DataFrame([(shiyasusa[0] > shiyasusa[1]).mean(),
(keisotusa[0] > keisotusa[1]).mean(),
(tashachui[0] > tashachui[1]).mean()],
index=measure_list[4:],
columns=['確率'])
display(prob_df1.round(5)*100)【実行結果】
テキスト75ページの数値とほぼ同じ結果になりました。
この確率より「TwitterはFacebookよりも発言しやすく、かつ、発言が軽率になりやすい」と言えそうです。
発言のしやすさと発言に対する軽率さ+他者反応への注意について、テキストにならって、SNS間の差が基準点$${c}$$以上である確率を可視化します。PHC曲線です。
テキストの図7.1に相当します。
### 発言のしやすさと発言に対する軽率さに関するSNS間の平均値の差の確率の描画
# ※図7.1に相当
## 確率データの作成
# x軸のcの値を設定
C = np.linspace(0, 1.4, 1001)
# 確率データの作成:3つの尺度の差の比率を算出
shiyasusa_plot = [(shiyasusa[0] - shiyasusa[1] > c).mean() for c in C]
keisotusa_plot = [(keisotusa[0] - keisotusa[1] > c).mean() for c in C]
tashachui_plot = [(tashachui[0] - tashachui[1] > c).mean() for c in C]
## 描画
plt.figure(figsize=(7, 3))
ax = plt.subplot()
# 1つめの尺度の曲線を描画
ax.plot(C, shiyasusa_plot, color='tab:blue', label=measure_list[4])
# 2つめの尺度の曲線を描画
ax.plot(C, keisotusa_plot, color='tab:green', label=measure_list[5], ls='--')
# 3つめの尺度の曲線を描画
ax.plot(C, tashachui_plot, color='tab:gray', label=measure_list[6], ls='-.')
# 修飾
ax.axhline(0.9, color='red', lw=0.8, ls=':')
ax.set(title='Twitter $\\mu_1 -$ Facebook $\\mu_2>c$となる確率',
xlabel='$c$', ylabel='確率', yticks=(np.linspace(0.0, 1.0, 11)))
plt.legend();【実行結果】
青線の発言のしやすさは差$${c=0.8}$$あたりで確率1になります。
Twitterの発言のしやすさはFacebookより0.8ほど高いと言えます。
緑点線の発言に対する軽率さは差$${c=0.4}$$あたりで確率1になります。
Twitterの発言に対する軽率さはFacebookより0.4ほど高いと言えます。

「自己開示の適切さ」4項目もモデリングしてMCMCサンプリングデータを得ています。
PHC曲線を描画してみましょう。
### 自己開示の適切さの4尺度の平均値μについて、SNS間の平均値の差の確率の描画
# 推論データから発言のしやすさと発言の軽率さのデータを取り出し
nichijou = idata_list1[0].posterior.mu.stack(sample=('chain', 'draw')).data
mokuteki = idata_list1[1].posterior.mu.stack(sample=('chain', 'draw')).data
negative = idata_list1[2].posterior.mu.stack(sample=('chain', 'draw')).data
shuikara = idata_list1[3].posterior.mu.stack(sample=('chain', 'draw')).data
## 確率データの作成
# x軸のcの値を設定
C = np.linspace(0, 0.5, 1001)
# 確率データの作成:3つの尺度の差の比率を算出
nichijou_plot = [(nichijou[0] - nichijou[1] > c).mean() for c in C]
mokuteki_plot = [(mokuteki[1] - mokuteki[0] > c).mean() for c in C]
negative_plot = [(negative[0] - negative[1] > c).mean() for c in C]
shuikara_plot = [(shuikara[0] - shuikara[1] > c).mean() for c in C]
## 描画
plt.figure(figsize=(7, 3))
ax = plt.subplot()
# 1つめの尺度の曲線を描画
ax.plot(C, nichijou_plot, color='tab:blue', label=measure_list[0])
# 2つめの尺度の曲線を描画
ax.plot(C, mokuteki_plot, color='red', label=measure_list[1], ls='-.')
# 3つめの尺度の曲線を描画
ax.plot(C, negative_plot, color='tab:green', label=measure_list[2], ls='--')
# 4つめの尺度の曲線を描画
ax.plot(C, shuikara_plot, color='tab:orange', label=measure_list[3],
ls=(0, (5, 10)))
# 修飾
ax.axhline(0.9, color='red', lw=0.8, ls=':')
ax.set(title='Twitter $\\mu_1 -$ Facebook $\\mu_2>c$となる確率\n'
'(目標・関心事の開示は$\\mu_2-\\mu_1>c$)',
xlabel='$c$', ylabel='確率', yticks=(np.linspace(0.0, 1.0, 11)))
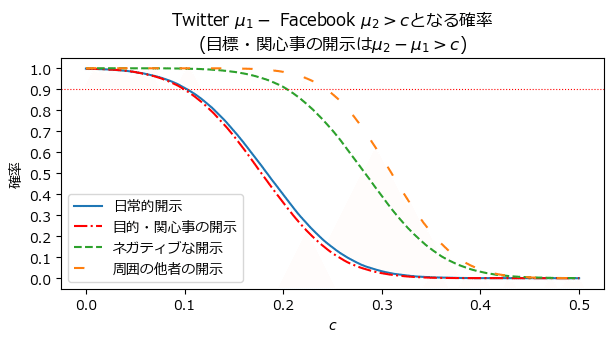
plt.legend();【実行結果】
日常的開示とネガティブな開示は、Twitterの方が0.2ほど高い結果になりました。
日常的な自己開示(自分のことを他者へ公開すること)とネガティブな自己開示は、Facebookと比べてTwitterの方が「0.2だけ適切寄りの得点」という事でしょうか。

モデル2の構築「参加者内2要因モデル」
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
$$
\sigma_s \sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100)\\
\sigma_e \sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100)\\
\sigma_{as} \sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100)\\
\sigma_{bs} \sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100)\\
\\
\mu \sim \text{Uniform}\ (\text{lower}=-100,\ \text{upper}=100) \\
\mu_a \sim \text{Uniform}\ (\text{lower}=-100,\ \text{upper}=100,\ \text{dims}=sns, \text{zerosum\_axes}=[0]) \\
\mu_b \sim \text{Uniform}\ (\text{lower}=-100,\ \text{upper}=100,\ \text{dims}=measure, \text{zerosum\_axes}=[0]) \\
\mu_s \sim \text{Norma;}\ (\text{mu}=0,\ \text{sigma}=\sigma_s,\ \text{dims}=id, \text{zerosum\_axes}=[0]) \\
\mu_{ab} \sim \text{Uniform}\ (\text{lower}=-100,\ \text{upper}=100,\ \text{dims}=(sns, measure), \text{zerosum\_axes}=[1]) \\
\mu_{as} \sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_{as},\ \text{dims}=(sns, id), \text{zerosum\_axes}=[1]) \\
\mu_{bs} \sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_{bs},\ \text{dims}=(measure, id), \text{zerosum\_axes}=[1]) \\
\\
\mu_{sum} = \mu + \mu_a[snsIdx] + \mu_b[measureIdx] + \mu_s[idIdx]\\
+ \mu_{ab}[snsIdx, measureIdx] + \mu_{as}[snsIdx, idIdx] + \mu_{bs}[measureIdx, idIdx] \\
s \sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_s,\ \text{dims}=id) \\
likelihood \sim \text{Normal}\ (\text{mu}=\mu_{sum},\ \text{sigma}=\sigma_e) \\
$$
1.データの読み込み(その2)
「snsdata2.csv」をpandas のデータフレームに読み込みます。
### データの読み込み
# 1つ目のデータから自己開示適切さの4つの尺度を抜き出して縦持ちに変換したもの
# 列名の設定
col_names2 = ['SNS', '尺度', '得点', 'ID']
measure_list2 =['日常的開示', '目的・関心事の開示', 'ネガティブな開示',
'周囲の他者の開示']
# csvファイルの読み込み
data2 = pd.read_csv('snsdata2.csv', skiprows=1, names=col_names2)
data2 = data2[['SNS', 'ID', '尺度', '得点']]
# データフレームの表示
display(data2)【実行結果】
自己開示の適切さの4つの項目を「尺度」で縦持ちに変換しています。
列の内容は次のとおりです。
・SNS:SNSの種類(1:Twitter、2:Facebook)
・ID:参加者のID(1から198)
・尺度:自己開示の適切さの4項目番号
1:日常的開示、2:目標・関心事の開示、3:ネガティブな開示、4:周囲の他者の開示
・得点:尺度に対応する得点(1~5)

2.モデルの定義
数式表現を実直にモデル記述します。
このモデルは1本です。開示項目ごとにモデリングすることはありません。
### モデル定義関数の定義
a = len(sns_list)
b = len(measure_list2)
s = data2['ID'].max()
# モデルの定義
with pm.Model() as model2:
### データ関連定義
# coordの定義
model2.add_coord('data', values=data2.index, mutable=True)
model2.add_coord('sns', values=sns_list, mutable=True)
model2.add_coord('measure', values=measure_list2,
mutable=True)
model2.add_coord('id', values=list(range(1, data2['ID'].max()+1)),
mutable=True)
# dataの定義
y = pm.ConstantData('y', value=data2['得点'].values, dims='data')
snsIdx = pm.ConstantData('snsIdx', value=data2['SNS'].values - 1,
dims='data')
measIdx = pm.ConstantData('measIdx', value=data2['尺度'].values - 1,
dims='data')
idIdx = pm.ConstantData('idIdx', value=data2['ID'].values - 1,
dims='data')
### 事前分布
# 標準偏差
sigmaE = pm.Uniform('sigmaE', lower=0, upper=100)
sigmaS = pm.Uniform('sigmaS', lower=0, upper=100)
sigmaAS = pm.Uniform('sigmaAS', lower=0, upper=100)
sigmaBS = pm.Uniform('sigmaBS', lower=0, upper=100)
# 合計ゼロ制約の定義
transforms1 = pm.distributions.transforms.ZeroSumTransform(
zerosum_axes=[0])
transforms2 = pm.distributions.transforms.ZeroSumTransform(
zerosum_axes=[1])
# transforms3 = pm.distributions.transforms.ZeroSumTransform(
# zerosum_axes=[0, 1])
# 平均値
mu = pm.Uniform('mu', lower=-100, upper=100)
muA = pm.Uniform('muA', lower=-100, upper=100, dims='sns',
transform=transforms1,
)
muB = pm.Uniform('muB', lower=-100, upper=100, dims='measure',
transform=transforms1,
)
muS = pm.Normal('muS', mu=0, sigma=sigmaS, dims='id',
transform=transforms1)
muAB = pm.Uniform('muAB', lower=-100, upper=100, dims=('sns', 'measure'),
transform=transforms2,
)
muAS = pm.Normal('muAS', mu=0, sigma=sigmaAS, dims=('sns', 'id'),
transform=transforms2,
)
muBS = pm.Normal('muBS', mu=0, sigma=sigmaBS, dims=('measure', 'id'),
transform=transforms2,
)
### muの計算
muSum = (mu + muA[snsIdx] + muB[measIdx] + muS[idIdx]
+muAB[snsIdx, measIdx] + muAS[snsIdx, idIdx]
+ muBS[measIdx, idIdx])
### 尤度
likelihood = pm.Normal('likelihood', mu=muSum, sigma=sigmaE, observed=y,
dims='data')
### 計算値
sigmaA = pm.Deterministic('sigmaA', pt.std(muA))
sigmaB = pm.Deterministic('sigmaB', pt.std(muB))
sigmaAB = pm.Deterministic('sigmaAB', pt.std(muAB))
deltaA = sigmaA / sigmaE
deltaB = sigmaB / sigmaE
deltaAB = sigmaAB / sigmaE
cellMean = pm.Deterministic('cellMean',
mu + pt.stack([muA, muA, muA, muA]).T + pt.stack([muB, muB]) + muAB,
dims=('sns', 'measure'))【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の4つを設定しました。データの行の座標:名前「data」、値「行インデックス」
SNSの座標:名前「sns」、値「'Twitter', 'Facebook'」
尺度の座標:名前「measure」、値「尺度番号」
参加者IDの座標:名前「id」、値「1~198」
dataの定義
次の3つを設定しました。目的変数:得点 y
SNSインデックス snsIdx
尺度インデックス measIdx
参加者IDインデックス idIdx
パラメータの事前分布
$${\sigma_s, \sigma_e, \sigma_{as}, \sigma_{bs}, \mu}$$は区間広めの一様分布を採用しました。
その他のパラメータはテキストまたはStan定義のとおりです。
合計0制約(MCMC時に効く制約)
PyMCのtransforms.ZeroSumTransform()で合計0制約を付けました。
1次元のみの変数$${\mu_a, \mu_b, \mu_s}$$は次元0が合計0になるようにtransforms1を設定しました、
2次元の変数$${\mu_{ab}, \mu_{as}, \mu_{bs}}$$は、次元0の合計0と次元1の合計0の実装方法が分からなかったので、次元1が合計0になるようにtransforms2を設定しました。
この2次元の変数の合計0制約がテキストと異なっており、推論結果がテキストと相違する要因になってしまいました。
尤度
観測値 y は「さまざななパラメータで表現した平均の合計$${\mu_{sum}}$$」を平均パラメータ、$${\sigma_e}$$を標準偏差パラメータにもつ正規分布に従います。
計算値
cellmeanは分析で利用する計算値です。
$${\mu + \mu_a + \mu_b + \mu_{ab}}$$です。
3.モデルの外観の表示
# モデルの表示
model2【実行結果】
パラメータが多いので事前分布の定義数が増えました。

# モデルの可視化
pm.model_to_graphviz(model2)【実行結果】
尤度関数:正規分布の平均パラメータ mu を構成するパラメータが横一列に並んでいます。壮観です!

4.事後分布からのサンプリング
乱数生成数はテキストと同じです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ1時間25分でした。
0制約を付けているのが時間がかかる要因のような気がします。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 1時間25分
# テキスト:iter=21000, warmup=1000, chains=5
with model2:
idata2 = pm.sample(draws=20000, tune=1000, chains=5, target_accept=0.998,
nuts_sampler='numpyro', random_seed=1234) 【実行結果】
5.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$とします。
### r_hat>1.1の確認 1分30秒
# 設定
idata_in = idata2 # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
(az.rhat(idata_in) > threshold).sum()【実行結果】
$${\hat{R} > 1.1}$$のパラメータが幾つか存在しています(右端列が0以外)。
収束条件を満たすことができませんでした。
もう一息な気がしますが、収束の調整は諦めました。
収束できていない推論データでは分析に使えません(泣)
そこで、ここからは、一般的な推論データ確認と、分析には使えませんがテキストのコードをPython化して動かしてみます。
なお、一部のコードは処理時間がかなりかかります。
コード1行目末尾に処理時間の目安を掲載しましたので参考にしてください。
手始めにざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示 4分40秒
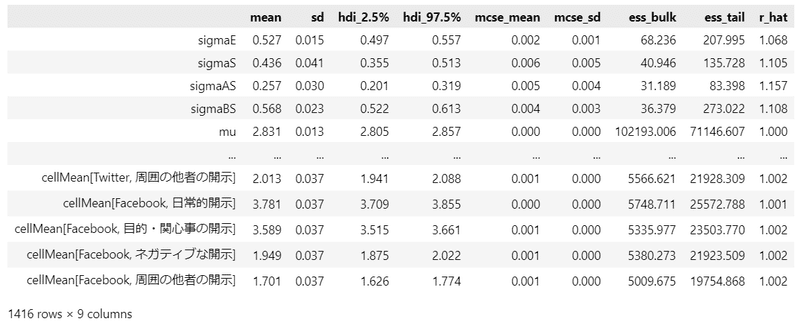
pm.summary(idata2, hdi_prob=0.95, round_to=3)【実行結果】
見えているパラメータの$${\hat{R}}$$は$${1.1}$$に近い感じです(悔しい)。
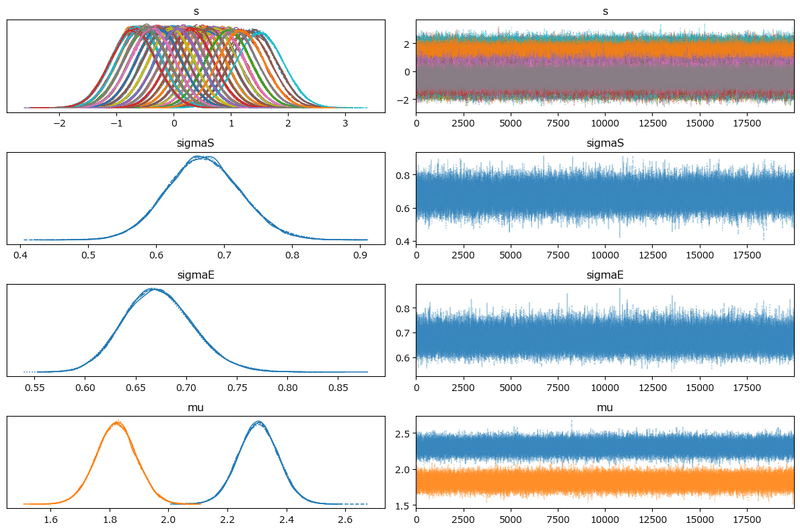
### トレースプロットの表示 4分50秒
pm.plot_trace(idata2, compact=True)
plt.tight_layout();【実行結果】
個別のパラメータを見ると、収束を示す描画、収束できていない描画が混在しているようです。
また、グラフ下部に黒いバーコードが大量に表示されています。発散を示すものであり、モデルがよくない状態です。


モデル2の分析に至らないデータ確認「参加者内2要因モデル」
テキストにならって、MCMCサンプリングデータの可視化を試みます。
ただし収束していないので、データの中身は適切ではありません。
ご留意くださいませ。
まずはテキストの表7.4「自己開示の適切さ評価:パラメータの事後統計量」です。
pm.summary()を用いて平均値(EAP)、標準偏差(post.sd)、95%HDIを見てみましょう。
全平均 mu とTwitter の効果 a です。
### 推論データの要約統計情報の表示
var_names = ['mu', 'muA']
pm.summary(idata2, hdi_prob=0.95, var_names=var_names, round_to=2)【実行結果】
全平均 mu とTwitter の効果 a の平均値・標準偏差は、テキストとほぼ同じ結果になりました。

続いて、開示内容の効果 muB です。
### 推論データの要約統計情報の表示
var_names = ['muB']
pm.summary(idata2, hdi_prob=0.95, var_names=var_names, round_to=2)【実行結果】
テキストと全く違う値になってしまいました。

続いて、SNSの種類と開示内容の交互作用 muAB です。
### 推論データの要約統計情報の表示
var_names = ['muAB']
pm.summary(idata2, hdi_prob=0.95, var_names=var_names, round_to=2)【実行結果】
テキストと全く違う値になってしまいました。

続いて、SNSの種類と自己開示の適切さの項目の平均値 cellmean です。
テキストの表の中線よりも下に示された$${\mu_{11}}$$等に該当します。
### 推論データの要約統計情報の表示
var_names = ['cellMean']
pm.summary(idata2, hdi_prob=0.95, var_names=var_names, round_to=2)【実行結果】
テキストとほぼ同じの結果になりました!

続いて、テキストの図7.2「各開示内容におけるTwitterとFacebookの差の確率」を描画してみます。
### 自己開示の適切さの3尺度の平均値μについて、SNS間の平均値の差の確率の描画
# 図7.2に相当
# 推論データから発言のしやすさと発言の軽率さのデータを取り出し
nichijou2 = idata2.posterior.cellMean.stack(sample=('chain', 'draw')).data
mokuteki2 = idata2.posterior.cellMean.stack(sample=('chain', 'draw')).data
negative2 = idata2.posterior.cellMean.stack(sample=('chain', 'draw')).data
shuikara2 = idata2.posterior.cellMean.stack(sample=('chain', 'draw')).data
## 確率データの作成
# x軸のcの値を設定
C = np.linspace(0, 0.5, 1001)
# 確率データの作成:3つの尺度の差の比率を算出
nichijou_plot = [(nichijou[0] - nichijou[1] > c).mean() for c in C]
mokuteki_plot = [(mokuteki[1] - mokuteki[0] > c).mean() for c in C]
negative_plot = [(negative[0] - negative[1] > c).mean() for c in C]
shuikara_plot = [(shuikara[0] - shuikara[1] > c).mean() for c in C]
## 描画
plt.figure(figsize=(7, 3))
ax = plt.subplot()
# 1つめの尺度の曲線を描画
ax.plot(C, nichijou_plot, color='tab:blue', label=measure_list[0])
# 2つめの尺度の曲線を描画
ax.plot(C, mokuteki_plot, color='red', label=measure_list[1], ls='-.')
# 3つめの尺度の曲線を描画
ax.plot(C, negative_plot, color='tab:green', label=measure_list[2], ls='--')
# 4つめの尺度の曲線を描画
ax.plot(C, shuikara_plot, color='tab:orange', label=measure_list[3],
ls=(0, (5, 10)))
# 修飾
ax.axhline(0.9, color='red', lw=0.8, ls=':')
ax.set(title='Twitter $\\mu_1 -$ Facebook $\\mu_2>c$となる確率\n'
'(目標・関心事の開示は$\\mu_2-\\mu_1>c$)',
xlabel='$c$', ylabel='確率', yticks=(np.linspace(0.0, 1.0, 11)))
plt.legend();【実行結果】
テキストによく似たプロットになりました。
4つの開示内容はTwitterの方が得点が大きい感じがします。
確率=1付近を確かめると、周囲の他者の開示とネガティブな開示は 0.2 程度、Twitterの方が得点が高い模様です。

テキスト76~77ページでは「日常的開示>目標・関心事の開示>ネガティブな開示>周囲の他者の開示」という連言命題を式7.11を用いて計算・確認しています。
こちらでも確認してみましょう。
### 日常的>目標・関心事>ネガティブ>周囲の他者 の確率 ※テキスト76ページの連言命題
# cellMeanの取り出し
cell_mean = idata2.posterior.cellMean.stack(sample=('chain', 'draw')).data
# Twitterについて、連言命題が正しい確率の算出
u_twitter = ((cell_mean[0, 0] > cell_mean[0, 1]).mean()
* (cell_mean[0, 1] > cell_mean[0, 2]).mean()
* (cell_mean[0, 2] > cell_mean[0, 3]).mean())
# Facebookについて、連言命題が正しい確率の算出
u_facebook = ((cell_mean[1, 0] > cell_mean[1, 1]).mean()
* (cell_mean[1, 1] > cell_mean[1, 2]).mean()
* (cell_mean[1, 2] > cell_mean[1, 3]).mean())
# 表示
print(f'Twitter: {u_twitter:.3f}')
print(f'Facebook: {u_facebook:.3f}')【実行結果】
TwitterもFacebookも連言命題が正しい確率は、テキストと同様に、有効桁数3桁で100%になりました。


モデル3の構築「階層線形モデル」
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
$$
\sigma_s \sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100)\\
\sigma_e \sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100,\ \text{dims}=measure4)\\
s \sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_s,\ \text{dims}=id) \\
\\
\alpha \sim \text{Uniform}\ (\text{loser}=-100,\ \text{upper}=100,\ \text{dims}=(sns, measure4)) \\
\beta \sim \text{Uniform}\ (\text{loser}=-100,\ \text{upper}=100,\ \text{dims}=(sns, measure3, measure4)) \\
\\
\hat{y_1} = \alpha_0 + \beta_{00} x_0 + \beta_{10} x_1 + \beta_{20} x_2 \\
\hat{y_2} = \alpha_1 + \beta_{01} x_0 + \beta_{11} x_1 + \beta_{21} x_2 \\
\hat{y_3} = \alpha_2 + \beta_{00} x_0 + \beta_{12} x_1 + \beta_{22} x_2 \\
\hat{y_4} = \alpha_3 + \beta_{03} x_0 + \beta_{13} x_1 + \beta_{23} x_2 \\
\mu_S = [\hat{y_1}+s,\ \hat{y_2}+s,\ \hat{y_3}+s,\ \hat{y_4}+s] \\
\\
likelihood \sim \text{Normal}\ (\text{mu}=\mu_S,\ \text{sigma}=\sigma_e) \\
$$
1.モデルの定義
数式表現を実直にモデル記述します。
### モデル定義関数の定義
## 尺度リストの作成
# measure4:自己開示の適切さy
measure4_list = data1.columns[2:6]
# measure3:発言に関する個人の態度X
measure3_list = data1.columns[6:]
# モデルの定義
with pm.Model() as model3:
### データ関連定義
# coordの定義
model3.add_coord('data', values=data1.index, mutable=True)
model3.add_coord('sns', values=sns_list, mutable=True)
model3.add_coord('measure4', values=measure4_list, mutable=True)
model3.add_coord('measure3', values=measure3_list, mutable=True)
model3.add_coord('id', values=list(range(1, data1['ID'].max()+1)),
mutable=True)
# dataの定義
y = pm.ConstantData('y', value=data1.iloc[:, 2:6].values,
dims=('data','measure4'))
X = pm.ConstantData('X', value=data1.iloc[:, 6:].values,
dims=('data', 'measure3'))
snsIdx = pm.ConstantData('snsIdx', value=data1['SNS'].values - 1,
dims='data')
idIdx = pm.ConstantData('idIdx', value=data1['ID'].values - 1,
dims='data')
### 事前分布
# 尤度関数の標準偏差
sigmaE = pm.Uniform('sigmaE', lower=0, upper=100, dims='measure4')
# 参加者の効果s
sigmaS = pm.Uniform('sigmaS', lower=0, upper=100)
s = pm.Normal('s', mu=0, sigma=sigmaS, dims='id')
# 線形モデルの切片
alpha = pm.Uniform('alpha', lower=-100, upper=100, dims=('sns', 'measure4'))
# 線形モデルの偏回帰係数
beta = pm.Uniform('beta', lower=-100, upper=100,
dims=('sns', 'measure3', 'measure4'))
### yhatの計算 alpha + x * beta
yhat1 = pm.Deterministic('yhat1',
(alpha[snsIdx, 0] + X[:, 0] * beta[snsIdx, 0, 0]
+ X[:, 1] * beta[snsIdx, 1, 0] + X[:, 2] * beta[snsIdx, 2, 0]),
dims='data')
yhat2 = pm.Deterministic('yhat2',
(alpha[snsIdx, 1] + X[:, 0] * beta[snsIdx, 0, 1]
+ X[:, 1] * beta[snsIdx, 1, 1] + X[:, 2] * beta[snsIdx, 2, 1]),
dims='data')
yhat3 = pm.Deterministic('yhat3',
(alpha[snsIdx, 2] + X[:, 0] * beta[snsIdx, 0, 2]
+ X[:, 1] * beta[snsIdx, 1, 2] + X[:, 2] * beta[snsIdx, 2, 2]),
dims='data')
yhat4 = pm.Deterministic('yhat4',
(alpha[snsIdx, 3] + X[:, 0] * beta[snsIdx, 0, 3]
+ X[:, 1] * beta[snsIdx, 1, 3] + X[:, 2] * beta[snsIdx, 2, 3]),
dims='data')
yhat = pm.Deterministic('yhat', pt.stack([yhat1, yhat2, yhat3, yhat4]).T,
dims=('data', 'measure4'))
### muの計算 yhat + s
mus = pt.stack([yhat1+s[idIdx], yhat2+s[idIdx], yhat3+s[idIdx],
yhat4+s[idIdx]]).T
### 尤度
likelihood = pm.Normal('likelihood',mu=mus, sigma=sigmaE,
observed=y, dims=('data', 'measure4'))
### 計算値
# 説明変数の標準偏差
stdx = pt.std(X, axis=0)
# 目的変数の標準偏差
stdy = pt.std(y, axis=0)
# yhatの分散
varYhat = pm.Deterministic('varyhat', pt.var(yhat, axis=0), dims='measure4')
# 決定係数R^2
r2 = pm.Deterministic('r2', varYhat / (varYhat + sigmaE), dims='measure4')
# 標準偏回帰係数 = 偏回帰係数 × 説明変数の標準偏差 ÷ 目的変数の標準偏差
bsT = (beta[0] * pt.stack([stdx, stdx, stdx, stdx]).T
/ pt.stack([stdy, stdy, stdy]))
bsF = (beta[1] * pt.stack([stdx, stdx, stdx, stdx]).T
/ pt.stack([stdy, stdy, stdy]))
bs = pm.Deterministic('bs', pt.stack([bsT, bsF]),
dims=('sns', 'measure3', 'measure4'))【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の4つを設定しました。データの行の座標:名前「data」、値「行インデックス」
SNSの座標:名前「sns」、値「'Twitter', 'Facebook'」
自己開示の適切さ尺度:「measure4」、値「尺度名」
発言に関する個人の態度尺度:「measure3」、値「尺度名」
参加者IDの座標:名前「id」、値「1~198」
dataの定義
次の4つを設定しました。目的変数:自己開示の適切さの得点 y
説明変数:発言に関する個人の態度の得点 x
SNSインデックス snsIdx
参加者IDインデックス idIdx
パラメータの事前分布
$${\sigma_s, \sigma_e, \alpha, \beta}$$は区間広めの一様分布を採用しました。
その他のパラメータはテキストの記載のとおりです。
尤度
観測値 y は「自己開示の適切さ尺度ごとの平均$${\hat{y}}$$+参加者の効果$${s}$$」を平均パラメータ、$${\sigma_e}$$を標準偏差パラメータにもつ正規分布に従います。
計算値
標準偏回帰係数 bs を計算しています。
2.モデルの外観の表示
# モデルの表示
model3【実行結果】
線形モデルですが、いろいろとパラメータが増えています。

# モデルの可視化
pm.model_to_graphviz(model3)【実行結果】
複雑なモデルです。

3.事後分布からのサンプリング
乱数生成数はテキストと同じです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ7分20秒でした。
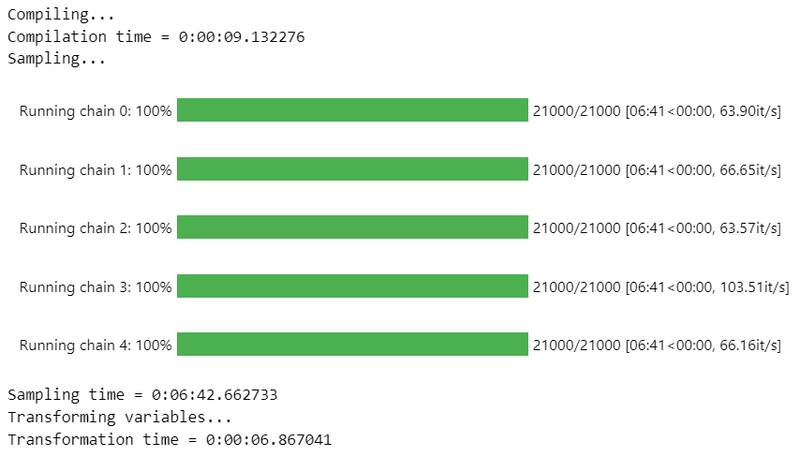
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 7分20秒
# テキスト:iter=21000, warmup=1000, chains=5
with model3:
idata3 = pm.sample(draws=20000, tune=1000, chains=5, target_accept=0.8,
nuts_sampler='numpyro', random_seed=1234) 【実行結果】
4.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$とします。
### r_hat>1.1の確認 2分50秒
# 設定
idata_in = idata3 # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
(az.rhat(idata_in) > threshold).sum()【実行結果】
$${\hat{R} > 1.1}$$のパラメータは0件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。
事後統計量を表示します。
処理時間がかかりました。
### 推論データの要約統計情報の表示 7分40秒
pm.summary(idata3, hdi_prob=0.95, round_to=3)【実行結果】
トレースプロットを確認しましょう。
25分ほどかかりました。
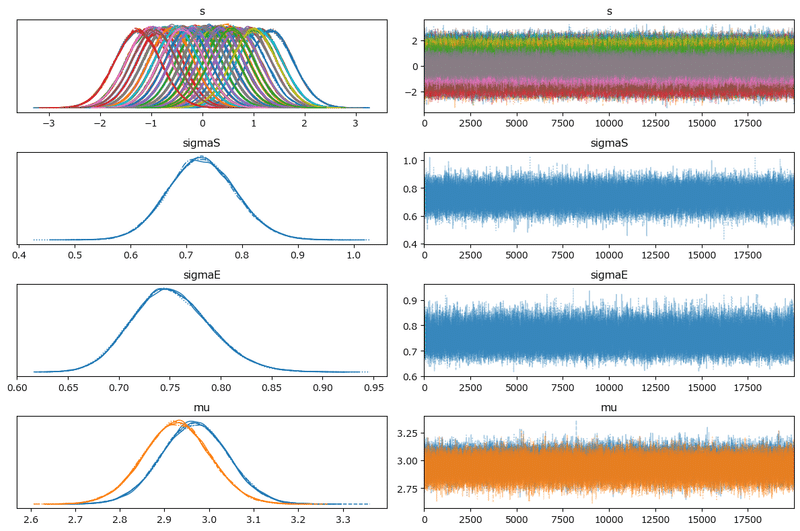
### トレースプロットの表示 25分50秒
pm.plot_trace(idata3, compact=True)
plt.tight_layout();【実行結果】
左のグラフから、5本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。


モデル3の分析「階層線形モデル」
テキストにならって「発言に関する個人の態度と自己開示の適切さ評価との関連」を分析します。
最初に事後分布の要約統計量を表示します。
テキストの表7.5に相当します
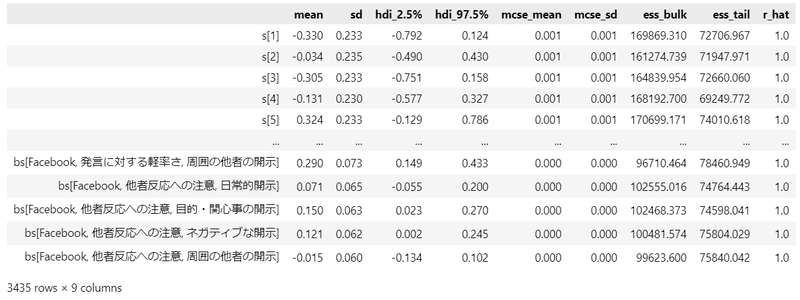
### 発言に関する態度の標準偏回帰係数の事後統計量 ※表7.5に相当
## 事後統計量の算出
# EAP
means = idata3.posterior.beta.stack(sample=('chain', 'draw')).mean(axis=3).data
# 標準偏差post.sd
stds = idata3.posterior.beta.stack(sample=('chain', 'draw')).std(axis=3).data
# 95%信用区間
ci95 = np.quantile(idata3.posterior.beta.stack(sample=('chain', 'draw')).data,
q=[0.025, 0.975], axis=3)
# 列名の設定
col_names3= ['SNS', '発言に関する個人の態度', '統計量'] + measure4_list.tolist()
tmp = []
# SNSごと(i)、発言に関する個人の態度(j)ごとに事後統計量計算を繰り返し処理
for i in range(2):
for j in range(3):
# EAPの計算
tmp.append([sns_list[i], measure3_list[j], 'EAP', *means[i, j, :]])
# post.sdの計算
tmp.append([sns_list[i], measure3_list[j], 'post.sd', *stds[i, j, :]])
# 95%CI下端の計算
tmp.append([sns_list[i], measure3_list[j], 'CI2.5%', *ci95[0, i, j, :]])
# 95%CI上端の計算
tmp.append([sns_list[i], measure3_list[j], 'CI97.5%', *ci95[1, i, j, :]])
# データフレーム化
stats_df3 = pd.DataFrame(tmp, columns=col_names3)
display(stats_df3.round(3))【実行結果】
テキストに近い結果を得られました!

テキストにならって上記の事後統計量を読みましょう。
数値は若干テキストと異なりますが、上記の事後統計量の値で考えてみます。
95%信用区間が0を含まない項目に着目します。
■ Twitter の場合
① 発言のしやすさ
Twitterが発言しやすいSNSと考えている人(発言しやすさの得点が高い人)は、日常的開示(0.341)と目標・関心事の開示(0.150)の適切さを高く評価し、一方で、周囲の他者の開示(-0.135)の適切さを低く評価している。
② 発言に対する軽率さ
発言に対する軽率さが高い人は、ネガティブな開示(0.169)と周囲の他者の開示(0.393)の適切さを高く評価し、一方で、目標・関心事の開示(-0.133)の適切さを低く評価している。
③他者反応への注意
他者反応への注意が高い人は、目標・関心事の開示(0.188)の適切さを高く評価している。
■ Facebook の場合
① 発言のしやすさ
Facebookが発言しやすいSNSと考えている人(発言しやすさの得点が高い人)は、日常的開示(0.438)と目標・関心事の開示(0.362)の適切さを高く評価している。
② 発言に対する軽率さ
発言に対する軽率さが高い人は、ネガティブな開示(0.220)と周囲の他者の開示(0.264)の適切さを高く評価し、一方で、日常的開示(-0.269)と目標・関心事の開示(-0.292)の適切さを低く評価している。
③他者反応への注意
他者反応への注意が高い人は、目標・関心事の開示(0.142)の適切さを高く評価している。
分析の最後は、テキスト78ページの標準偏回帰係数のSNS間の差です。
標準偏回帰係数は、MCMCサンプリングデータの計算値 bs です。
差は「TwitterーFacebook」です。
### 標準偏回帰係数のSNS間の差 ※テキスト78ページ
# bsの取り出し
bs_data = idata3.posterior.bs.stack(sample=('chain', 'draw')).data
# 自己開示の適切さi・発言に関する個人の態度jごとにSNS間の差の統計量を算出
diff_list = []
# 自己開示の適切さiごとに繰り返し処理
for i in range(4):
# 発言に関する個人の態度jごとに繰り返し処理
for j in range(3):
# Twitter - Facebookの算出
diff = bs_data[0, j, i, :] - bs_data[1, j, i, :]
# 95%CI区間の算出
ci95 = np.quantile(diff, q=[0.025, 0.975])
# 平均mean、標準偏差std、95%CI区間の下端・上端をリストに追加
diff_list.append([measure4_list[i], measure3_list[j], diff.mean(),
diff.std(), ci95[0], ci95[1]])
# データフレーム化
diff_df3 = pd.DataFrame(diff_list,
columns=['自己開示の適切さ', '発言に関する個人の態度',
'平均', '標準偏差', 'CI2.5%', 'CI97.5%'])
# データフレームの表示
display(diff_df3.round(2))【実行結果】
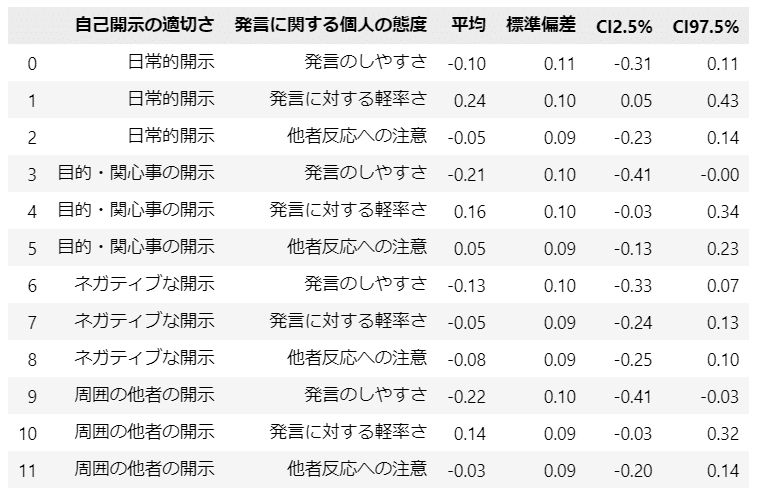
テキストの値と異なる箇所がありますが、上記の値で考えてみます。
95%信用区間が0を含まない項目に着目すると、次の3点について「SNS間で関連に相違がある」ことが浮かび上がります。
① 日常的開示を目的変数とした場合
「発言に対する軽率さ」のSNS間差:平均 0.24(標準偏差 0.10)95%CI[ 0.05, 0.43 ]
→日常的開示の適切さに関して、Twitterの方が発言に対する軽率さがプラス方向で寄与している?
② 目的・関心事の開示を目的変数とした場合
「発言のしやすさ」のSNS間差:平均 -0.21(標準偏差 0.10)95%CI[ -0.41, -0.00 ]
→目的・関心事の開示の適切さに関して、Twitterの方が発言のしやすさがマイナス方向で寄与している?
③ 周囲の他者の開示を目的変数とした場合
「発言のしやすさ」のSNS間差:平均 -0.22(標準偏差 0.10)95%CI[ -0.41, -0.03 ]
→周囲の他者の開示の適切さに関して、Twitterの方が発言のしやすさがマイナス方向で寄与している?

最後に、推論データを再利用する(かもしれない)場合に備えてファイルに保存しましょう。
idataをpickleで保存します。
### idataの保存 pickle
file = r'idata_list1_ch07.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_list1, f)
file = r'idata2_ch07.pkl'
with open(file, 'wb') as f:
pickle.dump(idata2, f)
file = r'idata3_ch07.pkl'
with open(file, 'wb') as f:
pickle.dump(idata3, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata_list1_ch07.pkl'
with open(file, 'rb') as f:
idata_list1_load = pickle.load(f)
file = r'idata2_ch07.pkl'
with open(file, 'rb') as f:
idata2_load = pickle.load(f)
file = r'idata3_ch07.pkl'
with open(file, 'rb') as f:
idata3_load = pickle.load(f)以上で第7章は終了です。
おわりに
SNSと自分語り
みなさんはどのSNSを使っていますか?
どのSNSで主に投稿していますか?
私は 現 X (旧 Twitter)を利用することが多いです。
また、このブログもSNSを的なつもりで使っています。
ブログ記事の内容は自分語りといえば自分語りでしょうか?
データ分析実験履歴を書いているのですから、ある意味、自分の過去をさらけ出しているように思えます。
テキストの「自己開示の適切さ尺度」の目標・関心事の開示-興味を持って勉強していること、に該当するでしょう。もちろん適切さに関して、私は4~5点をつけると思います。
実は、この章のタイトルに違和感を覚えています。
「自分語りが許されるのか?」の「許される」の言葉から、「世間に発言を許可してもらうという受け身」に感じたからです。
私は「自分語りが無難か?」程度に読み替えて、この章に取り組みました。

シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
