
第3章「本当のこと、教えてもらいます!」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング2」の第3章「本当のこと、教えてもらいます!」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
テキストは第2章から第4章まで「間接質問法」の各種手法で「違法行為等の経験」の調査データを用いたベイズモデリングに取り組んでいます。
この章では、「ランダム回答法」を用いて違法行為の経験率を推論します。

初学者に優しいシンプルなモデルということもあり、無事の収束と結果の一致を迎えることができました!
さあ、PyMCのベイズモデリングを楽しみましょう。
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 岡律子 先生、豊田秀樹 先生、久保沙織 先生、秋山隆 先生
モデル難易度: ★・・・・ (やさしい)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★★★★ & GoooD! \\
結果再現度 & ★★★★★ & 最高✨ \\
楽しさ & ★★★★★ & 楽しい! \\
\end{array}
$$

評価ポイント
テキストと同様の結果を得られました!
2回連続で、とてもうれしいです!
工夫・喜び・反省
前章と同じ行為の経験率について、異なる質問法・異なるベイズモデリングで導けることに感動です。世の中の多彩な研究を間近にできることの幸せを噛み締めています🌷

モデルの概要
テキストの調査・実験の概要
■ 間接質問法
間接質問法は、答えにくい質問の回答を得る場合に、回答者のプライバシーを守りつつ、分析に必要なデータを取得できる質問方法です。
テキストの前章の定義をお借りします。
間接質問法とは、質問する方法を工夫し、調査者が回答結果を見ても各回答者の真の状態はわからないように配慮しつつ、集団の特性について目的とする推定値を得る方法である。
この章の調査では、大学生の違法行為の経験率を取り扱っています。
上記定義に当てはめると、「調査者が回答を見ても大学生個人の回答値が分からないように配慮しつつ、ある大学生グループ全体の推定経験率を得る方法」と言い換えられます。

■ ランダム回答法
間接質問法の手法の1つです。
テキストの定義をお借りします。
ランダム回答法とは、本当に聞きたいことに対して正直に答えるか否かが回答者ごとにランダムに決まるような方法である。
2つの質問項目で構成される質問リストを用いて、回答者はランダムにどちらかの質問項目に回答します。
テキストの質問リストの例示をお借りして、説明を続けます。
【質問リスト】
質問A:違法ドラッグを吸引または摂取したことがある
質問B:あなたの学籍番号の末尾は0から4の間に含まれる
例示の質問Aのように、答えにくい質問=調査で調べたい項目を「キー項目」と呼びます。
一方、質問Bのように、キー項目とは関連のないニュートラルな内容を表す質問項目を「マスク項目」と呼びます。

回答の仕方が重要なのです。
回答者は、ランダムに振り分けられた1つ質問に対して回答します。
テキストの調査では、誰にも見られない場所でコイントスして、表が出たらキー項目に、裏が出たらマスク項目に、「はい」「いいえ」の2値を正直に回答してもらう方式が用いられました。
コイントスでランダムに質問が決まるので、各質問が選ばれる確率はそれぞれ1/2です。
そしてなにより、回答「はい」「いいえ」だけを見ても、どちらの質問項目に答えたのか分からないのがミソです。
マスク項目にも工夫がなされています。
学生をランダムに集める場合、学籍番号の末尾が0から4である確率は1/2です(5から9である確率も1/2です)。
確率1/2がモデリングで活躍します!

■ 調査の概要
「違法ドラッグの使用経験」(以下、Dと略します)と「売春の経験」(以下、Pと略します)を調査項目としています。
Google フォームで質問リストを作成して、調査協力者にWeb上で回答する方式を取られたようです。
ここまでの説明を図示します。

テキストのモデリング
■目的変数と関心のあるパラメータ
目的変数は調査の結果得られる回答データ$${x}$$です。
$${x}$$は、「はい」が1、「いいえ」が0の2値データです。
関心のあるパラメータはキー項目の経験率$${p}$$です。
■ テキストのベイズモデル
テキストおよびStanコードを基にして、私が理解できる形式に書き換えました。
数式の具体的な内容はぜひ、テキストでお確かめください。
$$
x \sim \cfrac{1}{2}\ \text{Bernoulli}(p) + \cfrac{1}{2}\ \text{Bernoulli}(\pi) \\
$$
尤度関数は2つのベルヌーイ分布の混合分布です。
右辺第1項はキー項目の質問に対する回答の分布、右辺第2項はマスク項目に対する回答の分布です。
キー項目とマスク項目のいずれに回答するかはコイントスでランダムに決まるので、2つのベルヌーイ分布は$${1/2}$$の重みが付いています。
$${\boldsymbol{p}}$$はキー項目の内容に関する経験率です。
事前分布は、テキストによると無情報的一様分布です。
$${\boldsymbol{\pi}}$$はマスク項目に当てはまる回答者の比率です。
学籍番号の末尾の数字は0から9まで10通りあり、そのうち質問項目の0から4に当てはまるのは 1/2 ですので、回答者がランダムに集められる場合、$${\pi}$$の値は$${1/2}$$です。

■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCの自己流モデルの推論値を利用した分析は「PyMC実装」章の「分析」をご覧ください。
PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.インポート
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
# PyMC
import pymc as pm
import arviz as az
# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')2.データの読み込み
テキストの R スクリプト内に記述されたデータを設定します。
回答の集計値です。
### データの作成
data = pd.DataFrame({'D': (98, 28), 'P': (99, 24)},
index=('いいえ', 'はい')).T
display(data)【実行結果】
1行目はDの経験の回答集計、2行目はPの経験の回答集計です。

2.データの外観の確認
円グラフで回答割合を可視化してみましょう。
### データの可視化(円グラフ)
# 色の設定
colors = ['lightpink', 'lightblue']
# 描画領域の指定
fig, axes =plt.subplots(1, 2, figsize=(10, 4))
# 2つのグラフを繰り返し描画する
for i, ax in enumerate(axes):
# 円グラフの描画
ax.pie(data.iloc[i], # 描画対象データ
startangle=90, # 時計の12時の位置から描画
explode=(0.1, 0), # 飛び出す
labels=data.columns, # はい、いいえのラベル文字
autopct='%1.1f%%', # %表示
colors=colors) # 色
# 修飾
ax.set(title=f'質問に{data.index[i]}経験を含む調査')
# 全体修飾
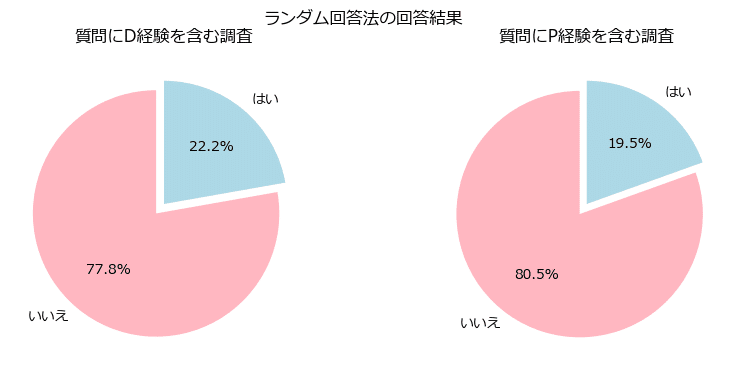
plt.suptitle('ランダム回答法の回答結果')
plt.show()【実行結果】
マスク項目(学籍番号末尾)の回答者が回答者全員の半分である50%とすると、その1/2である25%が「はい」と答える割合と想定できます。
円グラフの「はい」の割合は25%未満。
これは、D・Pの経験に「はい」と答えた割合がマイナス、というように読めます。なんだか不思議ですね。

Dのモデル構築
DとPのモデルを別個に構築します。
まずはDのモデリングです。
Pのモデリングの際には、DのモデルをP用にアレンジします。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
$${\text{Mixture}}$$は$${components}$$の確率分布を$${w}$$の割合で混合する混合分布です。
$$
\begin{align*}
p &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=1) \\
\pi &= 1/2 \\
w &= [\ 1/2,\ 1/2\ ] \\
components &= [\ \text{Bernoulli}\ (\text{p}=p),\ \text{Bernoulli}\ (\text{p}=\pi)\ ] \\
likelihood &\sim \text{Mixture}\ (\text{w}=w,\ \text{comp\_dist}=components)\\
\end{align*}
$$

1.モデルの定義
まず、分析に用いる回答データの前処理をします。
回答集計データであるdataに基づき、Dの経験のいいえの個数の0(98個の0)とはいの個数の1(28個の1)を生成して、回答データ:sample_dataを作成します。
モデルについては、数式表現を実直にモデル記述します。
### モデルの定義
## 初期値設定
# 回答データの生成
sample_data = np.concatenate([np.zeros(data.loc['D', 'いいえ']),
np.ones(data.loc['D', 'はい'])])
## モデルの定義
with pm.Model() as model1:
### coordの定義
model1.add_coord('data', values=list(range(len(sample_data))), mutable=True)
### dataの定義
# 回答
y = pm.ConstantData('y', value=sample_data, dims='data')
### 事前分布
# p:キー項目に当てはまる確率
p = pm.Uniform('p', lower=0, upper=1)
# pi:マスク項目に当てはまる確率
pi = 1/2
### 尤度
# 2つの分布の混合比率
w = [1/2, 1/2]
# 混合する2つの分布
components = [pm.Bernoulli.dist(p=p), # キー項目に当てはまる確率pの分布
pm.Bernoulli.dist(p=pi)] # マスク項目に当てはまる確率piの分布
# 尤度:混合分布
likelihood = pm.Mixture('likelihood', w=w, comp_dists=components,
observed=y, dims='data')【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の1つを設定しました。データの行の座標:名前「data」、値「行インデックス」
dataの定義
前処理で作成した回答データを{y}$$を設定しました。
なお変数名について、テキストでは$${x}$$、Stanでは$${target}$$を用いています。パラメータの事前分布
キー項目の内容に関する経験率$${p}$$の事前分布は区間$${[0,1]}$$の一様分布です。
尤度
2つのベルヌーイ分布の混合分布です。
$${\text{Mixture}}$$を用いて混合分布を定義します。
混合分布を構成する2つの分布を$${components}$$で定義し、混合比率を$${w}$$で定義します。
2.モデルの外観の確認
### モデルの表示
model1【実行結果】
シンプルです。

### モデルの可視化
pm.model_to_graphviz(model1)【実行結果】
シンプルです2。


3.事後分布からのサンプリング
乱数生成数はテキストと同じです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ1分でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 1分
# テキスト:iter=25000, warmup=5000, chains=4
with model1:
idata1 = pm.sample(draws=20000, tune=5000, chains=4, target_accept=0.8,
nuts_sampler='numpyro', random_seed=1234)【実行結果】

4.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$とします。
### r_hat>1.1の確認
# 設定
idata_in = idata1 # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
ひとまず、しきい値を$${\hat{R} > 1.01}$$で確認しました。
$${\hat{R} > 1.01}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.01}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
pm.summary(idata1, hdi_prob=0.95, round_to=3)【実行結果】
Dの経験率$${p}$$の平均値(テキストのEAP)は0.048(4.8%)です。

### トレースプロットの表示
pm.plot_trace(idata1, compact=False, figsize=(10, 3))
plt.tight_layout();【実行結果】
右のグラフはまんべんなく描画されていて、収束している感じがします。
左のグラフの4つの色=4つのマルコフ連鎖chainは重なっていて、ほぼ同一の推論値をはじき出しています。


Pのモデル構築
続いて、Dのモデルを転用してP用にアレンジします。
Dと異なるのは「初期値設定」の「回答値ごとの人数」の設定のみです。
モデルの数式表現
Dと同様ですので、記載を省略します。
1.モデルの定義
### モデルの定義
## 初期値設定
# 回答数ごとの人数
sample_data = np.concatenate([np.zeros(data.loc['P', 'いいえ']),
np.ones(data.loc['P', 'はい'])])
## モデルの定義
with pm.Model() as model2:
### coordの定義
model2.add_coord('data', values=list(range(len(sample_data))), mutable=True)
### dataの定義
# 回答
y = pm.ConstantData('y', value=sample_data, dims='data')
### 事前分布
# p:キー項目に当てはまる確率
p = pm.Uniform('p', lower=0, upper=1)
# pi:マスク項目に当てはまる確率
pi = 1/2
### 尤度
# 2つの分布の混合比率
w = [1/2, 1/2]
# 混合する2つの分布
components = [pm.Bernoulli.dist(p=p), # キー項目に当てはまる確率pの分布
pm.Bernoulli.dist(p=pi)] # マスク項目に当てはまる確率piの分布
# 尤度:混合分布
likelihood = pm.Mixture('likelihood', w=w, comp_dists=components,
observed=y, dims='data')【モデル注釈】省略
2.モデルの外観の確認
### モデルの表示
model2【実行結果】
Dと同じです。

### モデルの可視化
pm.model_to_graphviz(model2)【実行結果】
Dと同じです。


3.事後分布からのサンプリング
乱数生成数はテキストと同じです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ40秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 10秒
# iter=25000, warmup=5000, chains=4
with model2:
idata2 = pm.sample(draws=20000, tune=5000, chains=4, target_accept=0.8,
nuts_sampler='numpyro', random_seed=1234)【実行結果】

4.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$とします。
### r_hat>1.1の確認
# 設定
idata_in = idata2 # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
ひとまず、しきい値を$${\hat{R} > 1.01}$$で確認しました。
$${\hat{R} > 1.01}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.01}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
pm.summary(idata2, hdi_prob=0.95, round_to=3)【実行結果】
Pの経験率$${p}$$の平均値(テキストのEAP)は0.038です。

### トレースプロットの表示
pm.plot_trace(idata2, compact=False, figsize=(10, 3))
plt.tight_layout();【実行結果】
右のグラフはまんべんなく描画されていて、収束している感じがします。
左のグラフの4つの色=4つのマルコフ連鎖chainは重なっていて、ほぼ同一の推論値をはじき出しています。


分析
DとPの推論値について、テキストの分析にならって確認していきます。
分析~テキストにならって
経験率$${p}$$の事後分布をヒストグラムで描画します。
テキストの図2.2、図2.3に相当します。
### 経験率pの事後分布のヒストグラム描画 ※図3.2、3.3に相当
# 描画域の設定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4), sharey=True)
# Dの経験率の描画
pm.plot_dist(idata1.posterior.p, kind='hist', figsize=(6, 4),
hist_kwargs={'bins': 30}, ax=ax1)
ax1.set(xticks=(np.linspace(0, 0.3, 6)), xlabel='p', ylabel='Density',
title='Dの経験率pの事後分布')
# Pの経験率の描画
pm.plot_dist(idata2.posterior.p, kind='hist', figsize=(6, 4),
hist_kwargs={'bins': 30}, ax=ax2)
ax2.set(xticks=(np.linspace(0, 0.3, 6)), xlabel='p', ylabel='Density',
title='Pの経験率pの事後分布')
plt.tight_layout()
plt.show()【実行結果】
Dの経験率もPの経験率も0に偏っていて、裾が右側にずれた(正に歪んだ)分布になっています。
第2章の形状とよく似ています。

事後分布の統計量を確認します。
テキストの表2.2に相当します。なおMAPは省略しました。
### 経験率pの点推定と区間推定の表示 ※表3.1に相当 MAPの算出は省略
## 統計量計算関数の定義
def calc_stats(x):
ci = np.quantile(x, q=[0.025, 0.975])
hdi = az.hdi(x, hdi_prob=0.95)
return np.array([np.median(x), np.mean(x), np.std(x), ci[0], ci[1],
hdi[0], hdi[1]])
## 点推定値の算出
phi = data.div(data.sum(axis=1), axis=0).values[:, 1] # x_bar
phat = (2 * phi - 1/2).reshape(-1, 1) # 2φ-π
## DとPに関するpの事後統計値の算出
d_stats = calc_stats(idata1.posterior.p.data.flatten())
p_stats = calc_stats(idata2.posterior.p.data.flatten())
## 表示用のデータフレームの作成
# 点推定、事後統計量の各データを結合
stats_array = np.vstack([d_stats, p_stats]) # 2つの事後統計量を行方向に結合
stats_array = np.hstack([phat, stats_array]) # 点推定と事後統計量を列方向に結合
# データフレーム化
stats_df = pd.DataFrame(stats_array,
index=['D経験', 'P経験'],
columns=['2φ-π', 'MED', 'EAP', 'post.sd',
'CI下限', 'CI上限', 'HDI下限', 'HDI上限'])
# データフレームの表示
display(stats_df.round(3))【実行結果】
テキストとほぼ同じ結果を得られました。

なお、1番目の列$${\hat{p}=2\phi-\pi}$$はD・Pといったキー項目の経験率の推定量の一種です。
$${\phi}$$は「はい」の回答割合、$${\pi}$$はマスク項目に当てはまる回答の割合$${1/2}$$です。
この計算方法によると、経験率が負の値(通常考えにくい値)になってしまいました。
一方でベイズ推論による経験率の推定値は正の値におさまっています。
【分析】
ベイズモデルによる2つの経験率の推定値は次のようになりました。
Dの経験率は平均値$${4.8\%}$$、95%信用区間は$${[0.2\%, 15.3\%]}$$、95%HDIは$${[0.0\%, 13.1\%]}$$です。
Pの経験率は平均値$${3.8\%}$$、95%信用区間は$${[0.1\%, 12.6\%]}$$、95%HDIは$${[0.0\%, 10.5\%]}$$です。
第2章の推論値と比べると、Dの経験率は第3章のほうが小さく、Pの経験率は第3章のほうが若干大きい結果になりました。
また、標準偏差は第3章のほうが小さい値であり、95%信用区間と95%HDIは第3章のほうが狭いです。
いずれの章の$${p}$$推論値も分布のグラフを見ると0に偏っており、標本から得られたDの経験率、Pの経験率の推定値は0に近い数%程度のように見えます。

続いて、テキストで紹介のある「PHC曲線」を描画します。
PHCは「研究仮説が正しい確率」であり、事後分布サンプリングデータを用いて算出できます。
まず、PHC曲線の算出&描画関数を定義します。
### 推論データidataを受け取ってPHC曲線を描画する関数
def phc_plot(idata):
## データ加工
# 推論データからpの事後分布サンプリングデータを平坦化して抽出
p = idata.posterior.p.data.flatten()
# x軸目盛値となるcの値を生成
x = np.linspace(0, 0.5, 51)
# p > c の割合を計算
y = [(p > c).sum() / len(p) for c in x]
## 描画処理:描画結果をaxに格納
plt.plot(x, y)
plt.xlabel('c')
plt.ylabel('研究仮説が正しい確率:PHC')
plt.title(f'「経験率 p > c 」というPHC曲線')関数を実行してPHC曲線を描きます。
DのPHC曲線とPのPHC曲線を同時に描画します。
### PHC曲線の描画 ※図3.4、3.5に相当
plt.figure(figsize=(6, 4))
phc_plot(idata1)
phc_plot(idata2)
plt.legend(['DのPHC曲線', 'PのPHC曲線'])
plt.grid(lw=0.3);【実行結果】
Dのほうがやや緩やかなカーブであり、Pと比べて上部(確率値が大きい)に位置しています。

経験率が 5% より大きい($${p>0.05}$$)というPHCを計算します。
上のグラフの x軸が0.05のときの y軸の確率です。
なお、コード中の c の値を変更することで、5% 以外のケースを計算できます。
まずはDの経験率から。
### Dの経験率は5%より大きい(p>0.05)というPHCの算出
p = idata1.posterior.p.data.flatten()
c = 0.05
print(f'p > {c}の確率: {(p > c).sum() / len(p):.1%}')【実行結果】
テキストは 38.6% です。

続いてPの経験率です。
### Pの経験率は5%より大きい(p>0.05)というPHCの算出
p = idata2.posterior.p.data.flatten()
c = 0.05
print(f'p > {c}の確率: {(p > c).sum() / len(p):.1%}')【実行結果】
テキストの 27.8% と同じです。

【分析】
Dの経験率が 5% である確率は4割弱、Pの経験率が 5% である確率は3割弱です。
それぞれの経験率の真値が 5% であるかどうかは何とも言えないと思われます。
なお、$${p>0.001}$$の確率を計算すると、Dは98.4%、Pは97.7%でした。
なんとなくですが、経験率が 0.1%程度はありそうにも思えます。

最後に、推論データを再利用する場合に備えてファイルに保存しましょう。
idataをpickleで保存します。
### idataの保存 pickle
file = r'idata1_ch03.pkl'
with open(file, 'wb') as f:
pickle.dump(idata1, f)
file = r'idata2_ch03.pkl'
with open(file, 'wb') as f:
pickle.dump(idata2, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata1_ch03.pkl'
with open(file, 'rb') as f:
idata1_load = pickle.load(f)
file = r'idata2_ch03.pkl'
with open(file, 'rb') as f:
idata2_load = pickle.load(f)以上で第3章は終了です。
おわりに
話しにくいネタ
この原稿に取り掛かる直前に、私の身の回りに様々な出来事が発生しました。
概ね好ましくない出来事が重なるように押し寄せてきたのです。
健康面では謎の激痛に苦しみました。痛みでよく眠れず、集中力が低下しました。
仕事面では新しいタスクが割り当てられました。睡眠不足の状況下で、不慣れな業務に遭遇して気疲れしました。
この時期にパソコンの買い換えが重なり、旧パソコンから新パソコンの移行に時間を取られました。特にPython環境の再構築に手間取って、毎日のコード写経が滞ってしまいました。
健康が回復して生活に落ち着きを取り戻し、ブログ執筆の再開を果たすことができました。よかったです。

シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
