機械力学から見る剛体運動論 -2-

様々な剛体運動について考える「機械力学」ですが、その内容は高校物理の範疇から高度な数学の知識を使うところまで。長いスパンで関わるであろう、機械工学系の基礎になる学問です。

今回は数回に分けて、機械力学の話を深掘りしていきます。前回は機械力学で扱うこと、特に話題に出てくる機械振動に関して取り上げました。

今回は機械力学で扱う運動論（動力学）について、ひとつずつ紐解いていきます。それぞれの定義付けから詳しく見ていきましょう。

物体の運動の区別

機械力学は物体の運動（動力学）を扱います。運動論の話をする前に、まずは物体の扱い方を整理します。機械力学で扱う物体は「質点」と「剛体」の２種類です。これは以前に取り上げた材料力学で扱う「連続体」との大きな違いです。

質点は最も簡素な物体の扱い方です。形状を無視して質量を考慮します。物体に対する初歩的な仮定であり、高校物理の最初から登場します。一方で、剛体は形状と質量の両方を考慮できます。

運動には「並進運動」と「回転運動」の２種類があります。質点は形状が決まらない点として扱うため、考慮できる運動は並進運動だけです。剛体は並進運動と回転運動の両方を考慮できます。

物体の運動の再現精度としては、質点より剛体の方が確実ですが、考慮するべき範囲は広くなるので、どちらを仮定するかは状況次第です。

動力学での運動の記述

物体の動力学を扱うということは、対象の物体に対して運動方程式を立てることを意味します。例えば、並進運動の場合は次のようになります。

$${m\frac{d^2x}{dt^2}=\sum\limits_{i=1}^nF_i}$$

運動方程式の本来の書き方は上記の通りです。左辺は質量と加速度の積を表しますが、加速度は変位ｘの２階微分でもあります。右辺は加振力など着目する物体に働く力の合力です。

回転運動についても大枠は変わりません。変位ｘの代わりに回転角を導入しながら、２階微分（角加速度）を運動方程式に適用します。また、質量の代わりに慣性モーメントＩを利用します。

$${I\frac{d^2\theta}{dt^2}=\sum\limits_{i=1}^nN_i}$$

ここで、右辺は物体に働くモーメントの合計です。慣性モーメントは物体の回転に対する抵抗力を表し、主に質量と形状で決まります。

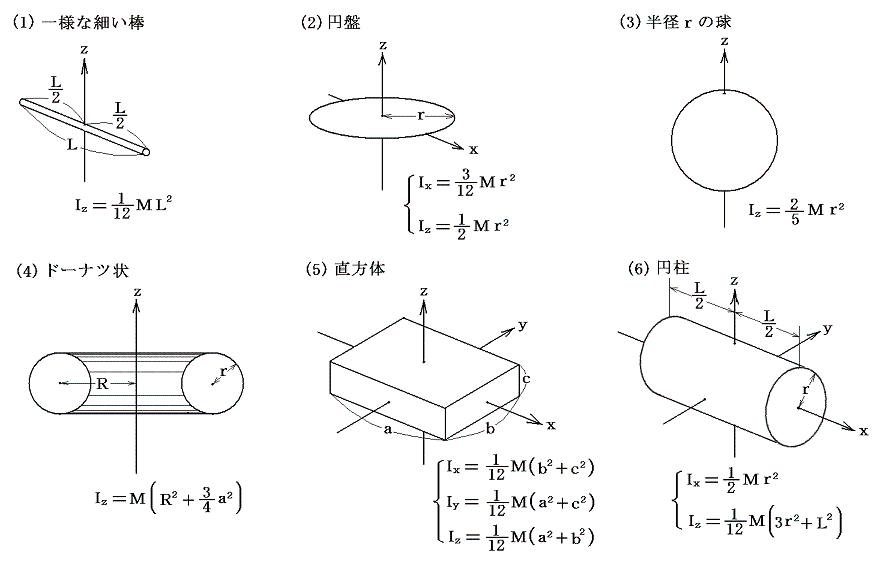
複雑な形状の場合は話が別ですが、単純な形状であれば公式みたいな感覚で計算できます（大抵の参考書に掲載されています）。

おわりに

機械力学の本格的な話に入るために、今回は動力学を考える上で必須である運動に関する法則（運動方程式）を見ていきました。

今回は概要説明に留まりましたが、実際はどのよな手順で運動方程式を立てていくのか、次回は例題を取り上げながら示していきます。

-------------------------
最後まで読んで頂き、ありがとうございます。この記事があなたの人生の新たな気づきになれたら幸いです。今後とも宜しくお願いいたします♪♪
-------------------------

⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ロードマップ ⭐︎⭐︎⭐︎