- 運営しているクリエイター
記事一覧
力の粒子:お話物理:標準理論
前回,標準理論と呼ばれる理論の登場人物(粒子)の表を見た.
今回は力を媒介する粒子,ゲージボゾンの話をしよう.ゲージボゾンは標準理論の相互作用を司る粒子である.強い相互作用,弱い相互作用,電磁相互作用の三種類があり,それぞれを司るグルーオン,ウィークボソン,そしてフォトンがある.
フォトンは電磁相互作用を司るゲージボゾンで,日本語で光子(こうし)と呼ばれる.
物体が電磁相互作用をするときは,
登場人物:お話物理:標準理論
先週はお休みをした.前々回で場の量子論を一応話し終えたことにして,今回から"標準理論"という理論の話をしようと思う.
標準理論は現代の素粒子物理の中で,実験的に検証された理論である.この世の全ての現象を説明できるわけではないが,数多くの現象を説明できる,理のある理論である.
今回は,標準理論の登場人物の紹介をしようと思う.まぁ人物というか,場であり,その励起が粒子になるのだが.
粒子(場)を
標準理論に向けて:お話物理:場の量子論
前回は場の理論のゲージ理論と一般相対論の関連について話した.数学的には同じ構造なのだった.
さてとりあえずではあるが,現代の量子場の理論に出てくる場,スカラー場,スピノル場,ベクトル場の話をした.
現在最も実験的に成功している標準理論と呼ばれる理論のお話をして行きたい.そのために現在発見されている粒子とその性質について話をしよう.
しようと思う....さてどこから話したものか.
一つは歴史
重力とおなじ:お話物理:場の量子論
前回,共変微分に必要な"A"というベクトル場の物理的な意味について話をした."A"は時空の各点とそのお隣さんで"どれだけ実数の基準がねじれているか"を表す量だった.
今回は理論を指定するラグランジアンに入れられる,形として曲率
を導入した.時空の一点の情報から,その周りでどれだけ実数軸がヨレているかを表す量だ.
実はこれは,重力の理論である一般相対論と同じ構造をしている.
一般相対論は,ざ
ヨレの具現化:お話物理:場の量子論
前回,局所複素回転に対して不変な理論を作るために導入した"A_μ"の意味について話した.
共変微分のおまけとして導入した"A_μ"は時空の各点の実軸と隣の実軸とのねじれを表している.
今回はこの共変微分から作れる,ラグランジアンの項について話そう.実は微分のおまけとして出てきた"A_μ"は自分自身だけで作れる項は一つしかない.
それはそれは共変微分自身との交換関係だ.
これ以外の組み合わせ
お隣さんとのねじれ:お話物理:場の量子論
前回,複素回転に対してラグランジアンを不変にする理論を考えた.時空の各点で複素回転してもラグランジアンが不変になるように微分におまけを加えたのだった.
おまけであるベクトル"A"が複素回転と同時に変換することで,全体としてラグランジアンが不変に保たれるのだ.
ではこのベクトル場"A"は物理的にどう言う意味についてコメントしておこう.
もともと微分とは場の各点とその隣の点のつながりの効果を持っ
回って生まれる場:お話物理:場の量子論
前回から,局所的な複素回転で不変な理論を作ろうと言うことになった.ただ,単純に理論に局所的な複素回転を導入すると,微分項からお釣りが出てラグランジアンが不変にならないのだった.
この微分が局所的な回転パラメタ"θ(x)"が微分をひっかけるのだ.
今回は局所的な回転パラメタの変化に伴って共に変化する共変微分を導入しよう.共変微分は次のような変換をするような"微分"である.
要は回転"e^iθ"
個別に回る:お話物理:場の量子論
前回は,複素スカラー場の理論が,複素場の回転によって理論として不変なのを見た.つまりこれは,"時空の全体の実数軸"を誰がどう決めても良いということだった.
この時空全体を一緒に変えても理論が不変なことを,大域的な対称性を言う.しかし,人間を含めた観測者は時空の全部を観測しているわけではない.僕らの人生で動ける範囲など,時間的にも空間的にも限られている.
物理が"どんな観測者から見ても同じ"理論
回る場:お話物理:場の量子論
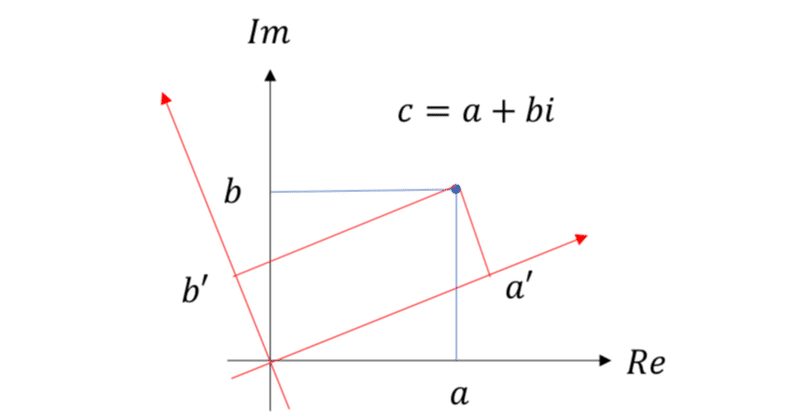
前回,実数と虚数を合わせた複素数には,回転の自由度があることを見た.回転の自由度は"何を実数にするか"という自由度が起因している.
今後の話が簡単になるように複素数の表記方法を変えようと思う.平面上の一点をx-y座標で表す方法から,極座標:長さと角度で書かれる方法がある.
複素数の実数自由度が"a,b"から長さ"r"と角度"θ"で書けるようになった.回転は文字通り,(実軸からの)角度を変える変
回る実:お話物理:場の量子論
今回から,ゲージ場と呼ばれる種類のベクトル場の構築をしていこうと思う.ゲージとはなんぞやという話はさておき,今日は複素数の話から始めよう.
複素数とは文字通り複数の素なる数を持った数で,言い換えれば二乗して正の数になる実数と,二乗して負の数になる虚数を合わせたものだ.虚数は虚数単位"i"と実数で書けて,結局複素数は,二つの実数の自由度をもつ数なのだ.
一つの数で実質二つの実数自由度を持つ複素数
見る人によってはいけないから:お話物理:場の量子論
前回までは,スピン1/2の場の量子論の話をしてきた.スピン1/2の粒子はスピノルと呼ばれる場の励起として表される.
今回からはスピン1の場の話をしようと思う.
スピン1の場は特殊相対論的なちょびっと回転に対応する応答が三次元回転のスピン1に相当する場のことだ.今後ベクトル場と呼ぶことにする.
スピン0や1/2の場,スカラーやスピノル場と同様に,ラグランジアンで書ける場の項をベクトル場で探すと
反粒子とは:お話物理:場の量子論
前回は,スピノル場のラグランジアン構築の話をした.スピノル場だけのラグランジアンは運動項は作れるが,質量項は作れない.それはスピノル場のもつカイラリティが原因だった.
カイラリティを持った場は,粒子として伝搬する時に向きがある.それはもちろん,進行方向に対してスピンの向きがあるのだから当然だ.
カイラリティは右手左手があるが,以降は左手に限って話を進める.右手の話にしたければ,左を右に読み替え
右手が左手に:お話物理:場の量子論
前回はスピン1/2をもつ粒子を表す場にはカイラリティ(掌)がある話をした.粒子の進行方向に対して回転の向きが二種類あるのだ.
今回は,スピン1/2の場の理論を構築するためにラグランジアンの話をしようと思う.系を指定するラグランジアンさえ作ってしまえば,あとは経路積分によって量子化することができる.
ラグランジアンは特殊相対論的変換(回転)に対してただの数,スカラーである必要がある.つまりスピノ
掌のある粒子:お話物理:場の量子論
今回から,スピノル場と言う種類の場のお話をしていこうと思う.
今まで扱って来たスカラー場は回転に対してのただの数,スカラーとして振る舞う場だった.空間の各点にただの数が定義されている場だ.例えば天気予報の各地での温度みたいなものだ.
スピノルはただの数ではない.(厳密には違うが)天気予報の風向きのように空間の各点に向きを持った量が定義されている場だ.つまり向きを表すように(ベクトルのように)数