量子力学に「観測問題」は存在しない
前世紀には観測問題を論じる人が多かったのですが、標準的な量子力学にはそのような観測問題はなかったことが現在では分かっております。例えば以下のように理解されています。
（１）波動関数の収縮について: 量子力学は情報理論の一種であり、波動関数は古典力学の粒子のような実在ではなく、情報の集まりに過ぎません。測定によって対象系の知識が増えることで、対象系の物理量の確率分布の集まりである波動関数も更新されるのが波動関数の収縮です。
「系を観測をすると、その波動関数（または状態ベクトル）は収縮し、その変化はシュレディンガー方程式に従わない」と聞いて、前世紀の「観測問題」に目覚めてしまって、「波動関数とは？収縮とは？」と懊悩してしまっている物理学徒は、まず箱の中の古典的なサイコロの目の確率を考察してみて下さい。
各目の出る確率は1/6で、一様分布でしたが、箱をとってサイコロを観測して3の目が出ていれば、確率分布は3の目にだけ集中して他の目は零になります。これが「確率分布の収縮」であり、そして当たり前ですが、この確率変化はニュートン方程式に従いませんよね。
波動関数や状態ベクトルは、物理量の確率分布の集合と数学的に等価な概念に過ぎません。ですから古典的なサイコロでも起きた「確率の収縮」が「波動関数の収縮」に対応するわけで、不思議なことでもありません。知識を得た測定後には、その結果に応じた条件付き確率を使うというだけの話です。知識、情報の増加でしかない「収縮」はシュレディンガー方程式を満たすわけがないのです。これを理解しない人は、サイコロの確率分布の収縮がニュートン方程式やフォッカー＝プランク方程式を満たしていないと、古典的な確率論に文句を言っているのと同じなのです。波動関数は所詮確率分布の集合に過ぎないのだと、しっかり腹に落として量子力学の理解を深めましょう。
なお測定で量子力学の確率分布が古典力学の確率分布とは違う点は、対象と測定機が相互作用をしている間に、測ろうとしている物理量以外の物理量の確率分布が乱される性質です。よくある勘違いなのですが、状態ベクトルや波動関数の収縮自体はその測定相互作用が切れてから起こります。観測者が測定機の結果を読み出して、その脳で認識したときに情報の更新としてその観測者にとっての波動関数は収縮するのですが、他の物理量の確率分布の乱れはこの観測者の脳内の過程で起こるわけではありません。対象と測定機が相互作用をしている最中にだけ他の物理量は乱れ（擾乱, じょうらん）を受けるのです。測定のこの相互作用が切れた後には、物理量の確率分布の擾乱量はそれ以上増えません。
（２）意識を持った人間が仮定されるのは不備？：それも問題になりません。まず自分以外の人間が本当に意識を持っているのか、それとも単なる機械のAIなのかを区別する方法がないためです。これは実証科学の俎上に載らず、単なる不良設定問題です。量子力学固有の話ではなく、それは科学全般の話です。
もし仮にAIや測定器が意識をもって、波動関数の収縮を起こすとしても、それらが意識がないと仮定して計算した場合と量子力学は同じ結果を与えます。また人間の場合でも同様です。つまり量子力学は特に人間だけを優遇しません。これについては下記もご参考にしてください。
波動関数や状態ベクトルは結局は物理量の確率分布の集合に過ぎません。「人間が波動関数を収縮させるのならば、ネズミはどうか？微生物はどうか？石はどうか？また電子一つは波動関数を収縮させるのか？」という問いも、「ネズミや電子が対象と相互作用をして情報を得ることで、そのネズミや電子にとっての、その対象の確率分布は更新されるのか？」という問いと同じなのです。サイコロの各目が出る確率は1/6ですが、それを振って表を観測すると、その確率分布はその出た目に集中し、他の目の確率は零になります。それは再度そのサイコロを見たら、同じ目が100%の確率で観測されるからです。観測による波動関数の収縮は、この観測によるそのサイコロの確率分布の変化と本質的に同じものです。ですから先の問いは、「振って観測した後のサイコロの確率分布を、ネズミや微生物や石や１つの電子は更新しないのか？」という質問と本質的に変わらないのです。もし彼らが観測と確率を利用して予測を立てる存在と考えるのならば、観測による知識の更新で精度がより高くなったその収縮した波動関数を使って、次の未来を予測するだろうという話に過ぎません。また彼らが観測と予測をするような意識は持たない存在だと考えるのならば、単なるモノや機械として、対象であるサイコロと相互作用をしたに過ぎないという話になるのです。量子力学では、彼らが意識をもった存在であると考えて計算をしても、意識を持たない存在であるとして計算をしても、外部観測者にとっては全く同じ答えが出るのです。答えは結局同じですので、どちらの計算方法を採用するかは、その計算をする人の好み次第です。どちらでも構いません。ある物理量の測定のために測定機と相互作用中に他の物理量の確率分布への擾乱（その分布を乱してしまうこと）が無視できないのが、量子力学の特徴なだけです。
測定機との相互作用が切れてしまった後に測定機を外部観測者が観測することで、測られた対象系に起こる波動関数の収縮自体には、サイコロの確率収縮と同様に特に不思議な部分はありません。結局誰が波動関数を収縮させるのかを「観測問題」だと呼ぶ人は、誰が観測によって知識を更新して、確率分布を収縮させるのか？と本当は問うべきなのです。そして明らかにこの問いは、量子力学自体に関する意味のある問題ではありません。ごく当たり前に一般的な確率という概念に元々備わっていた、観測で更新されるという性質です。それに敢えて「量子力学の観測問題」と名付けても仕方のないことです。
（３）「コペンハーゲン解釈は、いつ観測が起きて波動関数が収縮するのかを答えないし、またその収縮にかかる時間も計算できない。」 これも間違いです。標準的なコペンハーゲン解釈だけで、きちんと扱える話です。「いつ」波動関数が収縮するのかは、まず観測者を指定する必要があります。それはフォンノイマン鎖の話になります。
所謂ハイゼンベルグ切断の時刻以降では、マクロな多数の観測者たちや測定器の重ね合わせ状態が生じるだけで、それを観測する観測者ははいくらでも後に置くことができます。
ですから「いつ」波動関数が収縮すると問いたければ、「どの観測者にとって？」という部分を最初に明確化する必要があります。観測者を指定すれば、初期時刻から波動関数が収縮する時刻までにかかる時間間隔の量子的な期待値や確率分布を計算することが、コペンハーゲン解釈では原理的に可能です。
波動関数の収縮を意識する第1観測者と対象系とシグナルのマクロな合成系を外部で観測できる第2の観測者を設定して、この合成系全体のシュレディンガー方程式を解析すれば、第1観測者の脳が波動関数の収縮を意識した時刻の確率分布を計算できるわけです。
十分に時間が経った後に、第2観測者が第1観測者にいつ波動関数が収縮したのかを聞くということを繰り返せば、収縮時刻の確率分布と期待値も原理的には実験でも計測できるわけです。計算もコペンハーゲン解釈でできますし、その計測も原理的には可能なわけです。
「波動関数が収縮しているときに時間がかかるのか、かからないのか？」も、標準的な量子力学の範疇で答えが出る問題です。答えは「かかる」でして、その時間間隔は量子的に揺らいで確率的に分布をしています。その平均値は脳の中での信号伝達時間程度だと考えられます。なお波動関数の収縮時間の定義は、観測者Aの脳がその結果を認知するのにかかる時間です。情報を持ってくる信号の波動関数が観測者の体の波動関数と重なりを持ち始める時刻から、その観測者の脳が区別できる異なる情報の記憶状態の重ね合わせになるハイゼンベルグ切断の時刻までの時間間隔が、波動関数の収縮にかかる時間の定義です。そしてその当事者の観測者にとっては、波動関数が収縮に必要な時間間隔は量子的に揺らいでおり、毎回の実験では異なる値を持ちます。そしてその時間間隔は、その観測者を外で観測する外部観測者にはシュレディンガー方程式で計算できる、ある確率分布に従います。
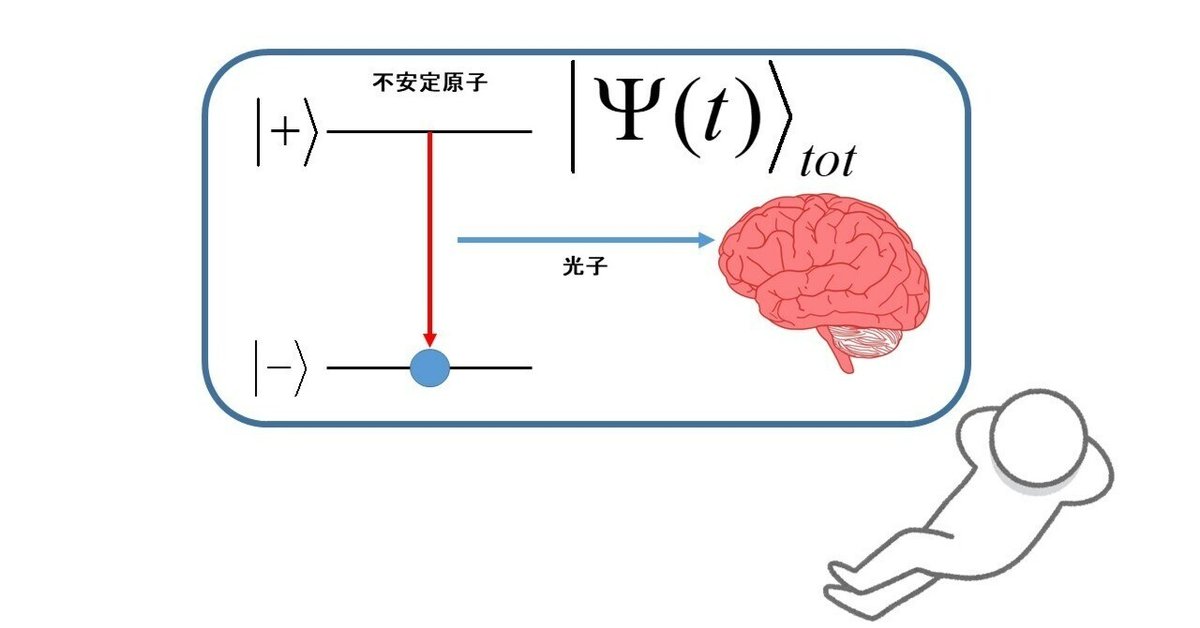
例えば不安定原子から出てくる光子を観測者Aが認識する（観測して、原子の波動関数は収縮する）のに必要な時間も、（原子＋A）という合成系を観測する外部観測者Bの立場では、シュレディンガー方程式から計算できます。Bの立場では、観測者Aも素粒子の集まりにすぎません。ですから不安定原子とAの合成系も普通の量子系ですから、シュレディンガー方程式で記述されます。するとAの脳に光の信号が記憶される時間の確率分布も計算できます。
量子力学で観測の終了時刻を決めるには、まずその観測をする観測者も量子系として扱う必要があります。そして対象系との合成系を考えて、初期時刻において、ある波動関数や状態ベクトルを設定します。
ここでは、ある部屋の中に閉じ込められたアインシュタインさんが、不安定原子から出てくる光をいつ観測するのかを問題としてみましょう。実験開始時刻は正午とします。アインシュタインさんと時計と原子も含めた、この部屋全体の初期量子状態を｜Ψ〉としましょう。するとシュレディンガー方程式に従って、この部屋全体の量子状態は、様々な時刻にアインシュタインさんが光った原子を見た状態の重ね合わせとなります。これは原理的には量子力学できちんと計算できます。
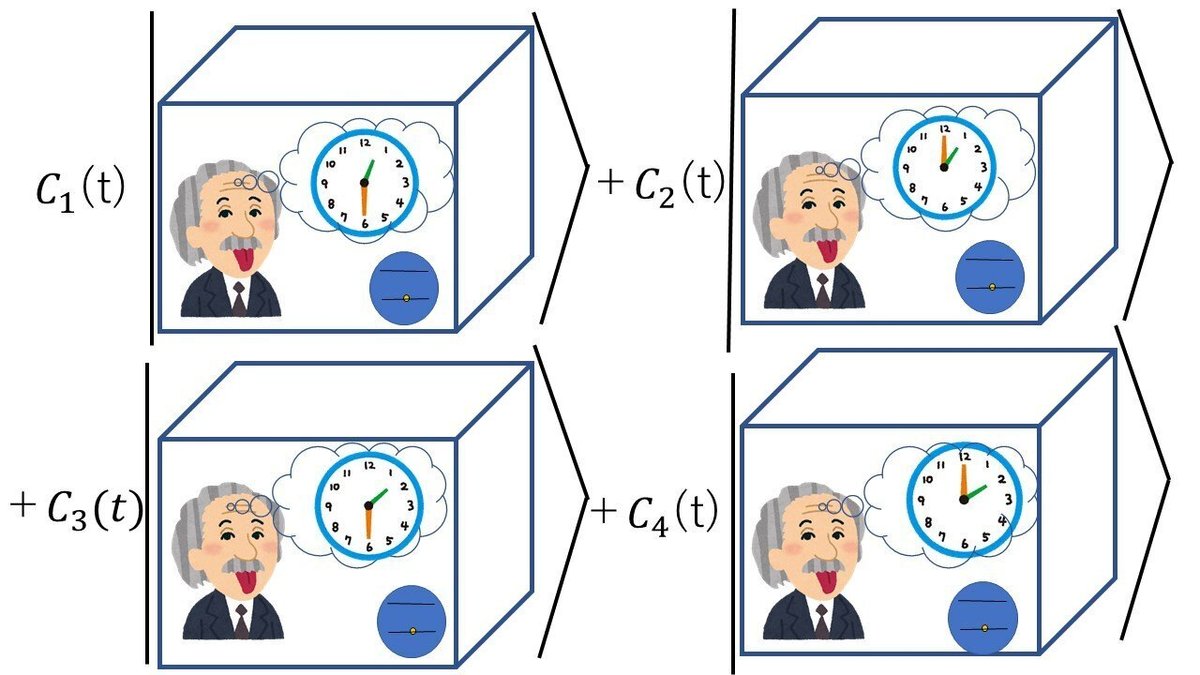
部屋の中にいるアインシュタインさんは、自分が重ね合わせ状態にあることに気づきません。例えば特定の１時という時刻に原子が光ったと感じると、その場合はもう２時に光ったとは決して感じないわけです。彼にとっては、どの時刻かに１回だけ原子は光るわけです。
十分な長さの実験時間（原子が、ほぼ必ず光った後の時間）をとった後に、外部観測者のアリスが部屋の窓を開けて、中にいるアインシュタインさんにいつ原子が光ったかを聞きます。そして二人はこの実験を何回も繰り返します。
原子が光る時刻は量子的に揺らぎますし、それをアインシュタインさんが観測して記憶した時刻も、確率的に分布します。
実験からも、量子力学の計算からも、アインシュタインさんにとって原子が光った時刻（彼にとっての観測が終了した時刻）の確率分布が得られます。この計算は実際には大変で難しいですが、量子力学という理論の原理的な困難にはなっていないのです。特に観測問題というものがあるわけではありません。
量子力学で観測終了までの時間を計算したければ、このようにどの観測者にとっての観測が終了する時刻であるのかを指定して、その観測者も量子系として扱い、観測者と対象系の合成系を観測する第２の外部観測者を用意すれば良いのです。
補足ですが、「観測者」は人間でないとダメということはありません。測定器やAIでも量子力学は同じ答えを出します。その「機械」が、波動関数の収縮を起こす意識を持っていると考えても、意識をもっていない粒子の集まりに過ぎないと考えても、どちらでも良いのです。
また今回は意識を持ったアインシュタインにとっての観測終了時刻の話をしましたが、その過程の手前に、原子が光った時刻を記録する測定器を考えて、その測定器にとっての観測終了時刻も、もちろん量子力学では計算できます。
（４）標準的なコペンハーゲン解釈の量子力学だと観測者がいなかったビッグバンの頃の量子性はどう説明するのか？これも問題ありません。ビッグバンがあったという史実は宇宙背景輻射という「量子的歴史書」に書き込まれているだけで、その歴史書を現在の観測者が測定機で読み解いているだけです。
観測者も地球も存在しなかった頃の時代の量子的現象が研究できるのも、量子情報としてなんらかの量子系に書き込まれて保存されていたためです。その「歴史書」としての量子系を今の我々が様々な測定装置で調べて解析をするのですから、その過程はコペンハーゲン解釈の量子力学できちんと記述できます。
量子力学では、クマムシでも猫でも人間でも、その体は全て素粒子の集まりであり、シュレディンガー方程式に従っています。例えば「ウィグナーの友人」という思考実験でも、観測者も素粒子の集まりだときちんと考えるだけで、パラドクスでもなんでもないことが理解できます。
ウィグナーの友人の思考実験は、観測者自体も量子系として明確に扱う話です。猫は「シュレ猫」という名前の素粒子の集まりに過ぎず、それを例えばフォンノイマンが観測をする。そのフォンノイマンを観るウィグナーにとってはフォンノイマンも量子系であり、「フォンノイマン」という名の素粒子の集まりに過ぎません。
「フォンノイマン」という名のその素粒子の集合は猫の波動関数を収縮させると考えてウィグナーが計算しても、またその素粒子の集合は猫の波動関数を収縮させないと考えてウィグナーが計算しても、同じ答えを量子力学は与えます。従って「観測問題」というものに煩わされる必要は量子力学には全くありません。
この記事が気に入ったらサポートをしてみませんか？