
量子力学の線形性はどこから来たのか?
量子力学の不思議として強調されることの1つに、状態の重ね合わせがあります。例えば有名なシュレディンガーの猫の思考実験では、生きている猫と死んでいる猫の状態の重ね合わせが出てきます。本当は生きているのか死んでいるのかは決まっているのに、それを外部の観測者は知らないだけということではありません。猫を測定をする前には、その生死は本当に決まっていない。そして生死の測定をすることで、そのどちら1つの「事実」が創発をするという意味です。
数学的にこのことを説明する場合には、複素数を成分とするベクトルを使います。猫が生きている状態を1つの単位複素ベクトルに対応させ、死んでいる状態をそのベクトルと直交をする別な単位複素ベクトルに対応させます。そしてシュレディンガーの猫状態は、その2つのベクトルを線形的に足した新しいベクトルに対応するのです。そして孤立系では、この状態の線形性がシュレディンガー方程式の線形性によって保たれています。波のように独立に運動をする素源的な状態ベクトルを様々に重ね合わせることで全体の運動を記述できます。
この状態ベクトルの線形性は量子力学の解説本でも、とても不思議で神秘的な現象であると紹介をされていますよね。しかし実はそれは表層的な「不思議」であって、量子力学の根本から考えれば、情報理論としての量子力学をベクトルや行列で書くという表記、記述を選んだ結果だと理解できるのです。本当は人々が驚くべき事実ではありません。状態ベクトルや密度行列に対するシュレディンガー方程式が線形なのは、確率分布が一般的に持っている「アフィン性」という性質に保つように、便利な表記をとった結果に過ぎません。また非線形な方程式は、この確率のアフィン性を破っていますので除外できます。
ここでは簡単のために二準位スピン系を用いて、何故量子力学に線形性が現れたのかを考えてみましょう。なおこの系の量子力学の定式化は、下記の教科書に詳しく書きました。
z軸方向に向いている非一様な磁場を内部に持つシュテルン=ゲルラッハ(SG)装置にこのスピン粒子を通すと、上下2つのビーム出口のどちらか1つから粒子は出てきます。上に出てくる粒子に対してスピンz成分の値は+1と定義され、また下に出てくる粒子に対しては-1と定義されます。またSG装置を回転させてx方向に向ければスピンx成分が同様に測れますし、装置をy方向に向ければスピンy成分が測れます。同じ状態にある多数のスピン粒子を用意して、SG装置をx方向、y方向、z方向に向けた3つの独立な実験を行ってデータをとれば、各スピン成分の期待値が測定できます。その実験値を下記の式に代入すると、単位ベクトルnで指定される任意の方向にSG装置を向けたときのスピンの値に対する観測確率が求められます。
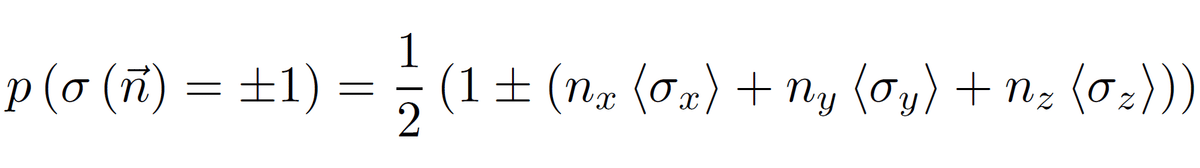
この式は、方向量子化(1回で識別できる状態は2個までということと、この量子化現象はあらゆる空間方向に対して平等に起きること)とスピン期待値のベクトル性という実験結果から導出できますが、これについては上の教科書の第2章をご覧ください。
次にアフィン性を説明します。例としてまずはスピンz成分の場合を採り上げます。そしてスピンの+1と-1の状態をコインの表と裏の状態に例えて図を描いて説明をします。1と2と名づけられた2つのスピン粒子を二つコインにそれぞれ例えます。そしてそれぞれ表と裏が出る確率は異なっているとします。この2種類の確率分布を持つスピン粒子を沢山用意して、その集団試料を下記の要領で作ることにします。まずqを0と1の間の実数をとるパラメータとします。そして確率qで第1の粒子を準備します。そして1-qの確率で第2の粒子を準備します。そのようにして作ったスピン粒子の集団に対しての確率は下記の式で与えられます。

このような方法で試料の集団を作ることを「確率混合」と呼びます。
そしてこのスピン粒子の集団に同じ磁場などの外力をかけたりすることで、この確率分布を変化させましょう。第1のスピン粒子だけの集団、第2のスピン粒子だけの集団、そして新しく確率混合で作られた集団それぞれの各方向のスピン成分の観測確率は変化しますが、それを下記のように表記します。

ここで確率混合の集団の操作をした後の確率分布は、下記のように与えられます。

重要なのは、確率混合で作られたこのスピン粒子の集団に対する確率分布は、下記のような別な方法でも計算できる点です。集団全体で見るのではなく、個々のスピン粒子1つ1つを見るのです。1つのそのスピン粒子は確率qで第1の粒子であり、確率1-qで第2の粒子です。この1つの粒子に物理操作をした後の確率は、下記の式のように、第1の粒子に同じ物理操作をした後の確率にqをかけたものに、第2の粒子に同じ物理操作をした後の確率に1-qをかけたものの和となります。
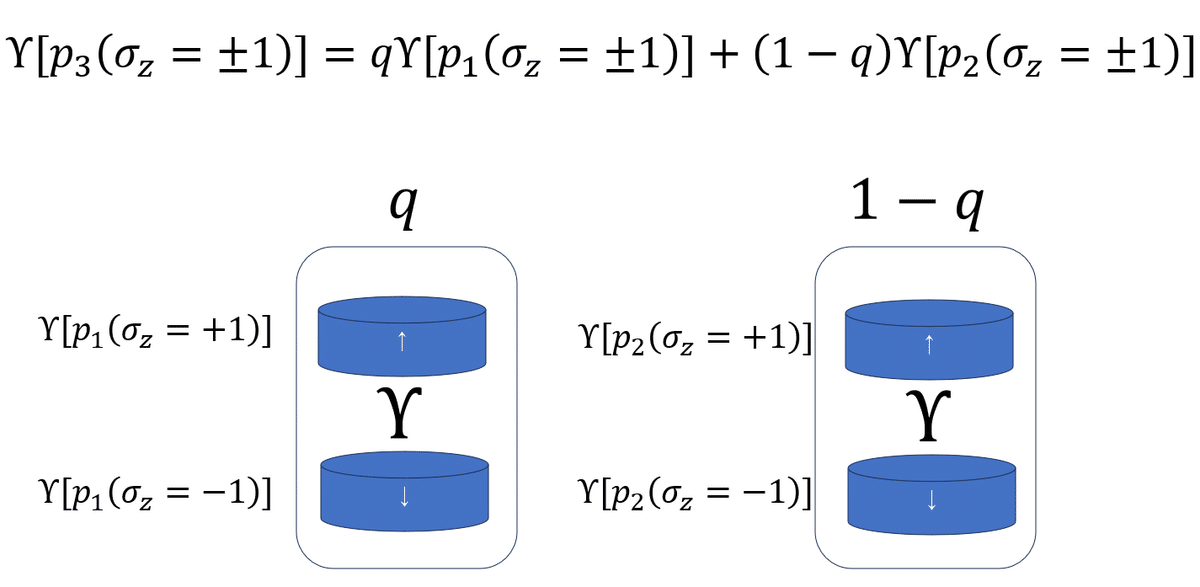
つまりこの確率混合された集団での確率には、下記の2つの表記があるのです。


この事実は、z方向に限らず任意の方向性に対するスピン成分についても成り立ちます。つまり一般に物理操作に対する確率分布の下記のアフィン性がいつでも成り立つのです。

このアフィン性は確率分布の一般的な性質であり、量子力学固有のものではありません。
先に紹介した教科書の第2章にあるように、密度行列表示でこれらの確率分布をまとめて書くことにしましょう。つまりスピンのx成分、y成分、z成分の期待値を使って、下記のエルミート行列を定義するのです。

この行列は飽くまで便利のための表記で、これでなかれば駄目という理由はありません。しかしこれを使うと、先の確率分布のアフィン性からシュレディンガー方程式の線形性が自動的に出てきます。
まず第1のスピン粒子に対しては、x成分、y成分、z成分の期待値が次のように計算をされます。
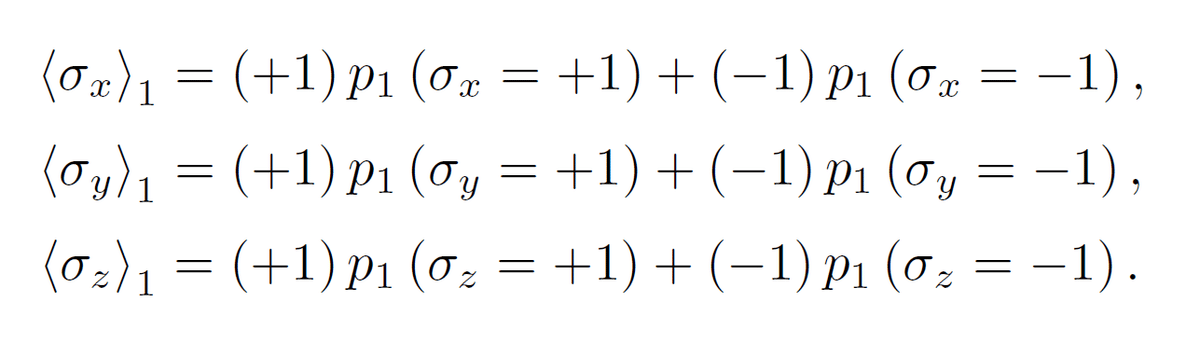
この値に基づいて、第1のスピン粒子に対しての密度行列は

で与えられます。同様に第2のスピン粒子に対して

という各方向のスピン成分の期待値を計算すれば、第2粒子の密度行列は
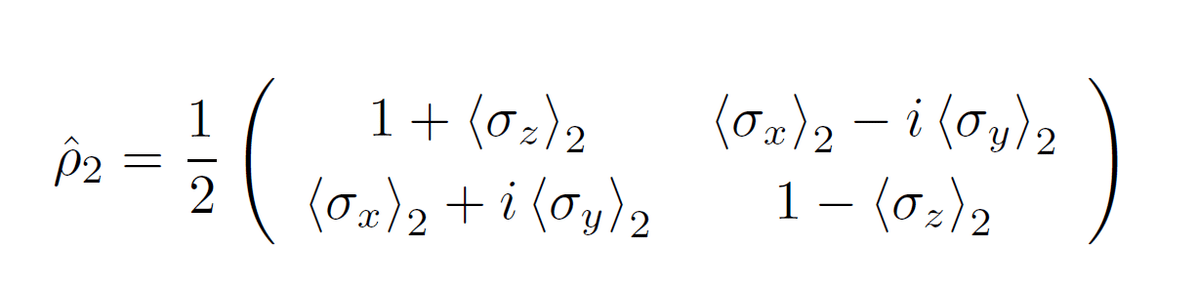
となることが分かります。また先の要領での確率混合で作られたスピン粒子の集団に対するスピンの期待値は

と計算されます。そしてその集団に対する密度行列は

で与えられます。またa=x,y,zとして、スピン成分の期待値に関して

という関係式が成り立っています。そしてこの性質を使うと、密度行列に対して

が証明できます。この密度行列は確率分布の1つの表示に過ぎませんから、この行列表記でもともとの確率分布のアフィン性を表現することは可能です。第1のスピン粒子の集団の密度行列、第2粒子のスピン粒子の集団の密度行列、そして確率混合で作られたスピン粒子の集団に対する密度行列に対しての物理操作を、それぞれ

と表しましょう。操作後も各集団は別な密度行列に対応する状態になります。そして操作後でも確率混合の集団については、確率分布から引き継いだ

という関係が成り立っています。このことから物理操作Γに対するアフィン性は密度行列では
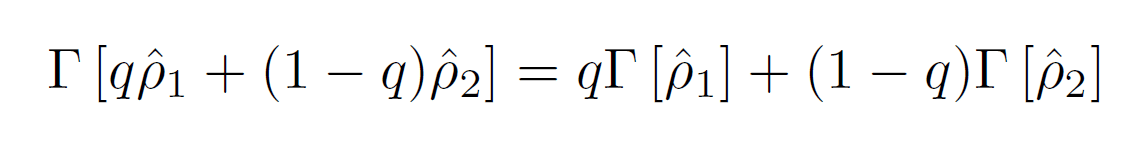
と表現できることが示されました。先の教科書の第6章で解説をしてますが、このアフィン性の関係式は任意の2次元複素正方行列と任意の複素係数に対しての

という関係に拡大できることが、いつでもできます。これが量子力学の方程式に線形性をもたらすのです。任意の物理操作が満たすべき完全正定値性とトレース保存の条件と合わせることによって、教科書第6章3節にありますように、

という物理操作のシュタインスプリング表現が得られます。操作前の初期の密度行列と、外部量子系Aの初期状態と、スピンとA系の状態ベクトル空間を跨いで作用をするユニタリ行列とで操作後の密度行列は計算できるのです。そして純粋状態と呼ばれる状態に対しての密度行列は、唯1つの複素単位ベクトルを用いて構成することができます。これが状態ベクトルとなります。
この物理操作Γを時間の関数だと思えば、教科書第6章にあるように、量子力学の運動方程式であるシュレディンガー方程式も導かれます。シュレディンガー方程式は線形性を持つ微分方程式ですので、最終的に量子力学のダイナミクスの状態線形重ね合わせの本質が、これで解明されたことになります。
これまでの流れを振り返りますと、線形性が現れた原因は確率分布に対する物理操作のアフィン性にあることに気付けるかと思います。そしてそのアフィン性は、決して量子力学固有の性質ではなく、全ての確率論が持つ一般的な性質に過ぎません。この意味で量子力学のダイナミクスの線形性は、確率論を認めさえすれば、特に不思議なことではないのです。
前世紀には波動関数のシュレディンガー方程式に波動関数の3次の非線形項を加える理論なども研究されていました。しかしその密度行列表示ではアフィン性は露わに破れています。現代的観点からは、このような非線形的拡張がうまくいかなかったのは、状態ベクトルや密度行列の操作論的定義(量子状態トモグラフィ)とアフィン性を入れてなかったからとも言えます。
ちなみに二準位スピン系に対する実験結果は、J.S.ベルが提案をした決定論的でかつ実在論である隠れた変数理論でも説明ができます。これは量子力学と全く同じ予言をする理論です。そしてベルの理論を密度行列や状態ベクトルの表記で書くこともできます。すると状態の線形重ね合わせも出てきます。この二準位スピン系の隠れた変数理論に対して、時間発展のシュレディンガー方程式を出すこともできます。この観点からは、線形性は決して量子力学固有の性質ではないと言えるのです。
このように状態ベクトルや密度行列の時間発展の非線形性はアフィン性から否定できますが、状態ベクトル空間の中にあるシュレディンガーの猫状態のような重ね合わせ状態が物理的に可能であることは、アフィン性とは独立です。これは別個に議論する必要があります。
スピン系のように、1回の実験だけで完全に区別できる純粋状態が有限個の場合に、回転などの連続的物理操作で新しく作られる、そして先の純粋状態とは1回で区別できない純粋状態は、どうしても状態ベクトル表示で線形重ね合わせになります。無限次元の量子力学でも、1回で区別できる純粋状態の集合には入らない、別な純粋状態が連続的物理操作で作られれば、それもこの線形表示では1回で区別できる純粋状態の状態ベクトルの重ね合わせになってしまいます。直交する2個の状態ベクトルが成す部分ベクトル空間内をくるくる連続的に回す物理操作があれば、線形重ね合わせ状態は出てきます。
区別できる状態の離散性と連続的物理操作を同時に考える必要性が、状態ベクトルの線形重ね合わせを必然的に招く構造になっているのです。ただしここで注意が必要なのは、そのような構造を持つ理論は量子力学に限定されていない点です。
上での述べたベルの隠れた変数の理論も、区別できる状態の離散性と連続的物理操作を持っており、実際にそのスピンz軸のアップ状態の状態ベクトルは、スピンx軸のアップ状態とダウン状態のそれぞれの状態ベクトルの線形重ね合わせになっています。
古典力学は他の理論と比べてむしろ特殊であり、1回の実験で区別できる無限個の純粋状態が隣接して、それが連続的に分布をしている性質があります。つまり相空間上の各点(x1,x2,x3,p1,p2,p3)の全てが1回の実験だけで互いに区別できる純粋状態になっています。このおかげで純粋状態の線形重ね合わせが出現せずに済んだのです。ラフに言うならば、空間回転のような連続的な物理操作を1つの純粋状態にある粒子に施しても、その粒子は無限に近く、かつ区別可能である純粋状態を次々に飛び移れたために、区別できる状態の線形重ね合わせは必要なかったのです。
なお量子力学は物理量の確率分布に基づいた情報理論であることをしっかりと押さえれば、所謂「観測問題」はそもそも量子力学には存在しなかったことも、明確に理解できます。ですので量子力学でもっとも驚くべき事実は、状態の線形重ね合わせではなく、また測定における不可避な他の物理量への擾乱でもなく、ベル不等式の破れの実験で確立をした「局所実在の否定」だと、私は考えています。
この記事が気に入ったらサポートをしてみませんか?
