Pythonライブラリ(数値解析ソフトウェア)：SciPy

2023年7月1日 14:29

１．概要

　数値解析ソフトウェアライブラリのSciPyを紹介します。
　SciPyは、Pythonプログラミング言語用のオープンソースの科学計算ライブラリです。2001年の最初のリリース以来、SciPyはPythonで科学的アルゴリズムを活用するためのデファクトスタンダードとなり、600以上のユニークなコード貢献者、数千の依存パッケージ、100,000以上の依存リポジトリ、年間数百万件のダウンロードがあります。LIGOによる重力波の検出や、Event Horizon Telescopeによるブラックホールの最近のイメージングなど、いくつかの主要な科学的結果の生成に使用されています（出典）。

１－１．SciPyでできること

　Scipyでできることは多岐にわたり数式処理（積分、線形代数、数理最適化など）、統計（統計処理、確率モデルなど）、分析（クラスター分析、離散フーリエ変換）などがあります。
　全て記載するのは無理なため、使用頻度が高いものを紹介します。

https://docs.scipy.org/doc/scipy/tutorial/index.html#user-guide

https://docs.scipy.org/doc/scipy/reference/index.html#scipy-api

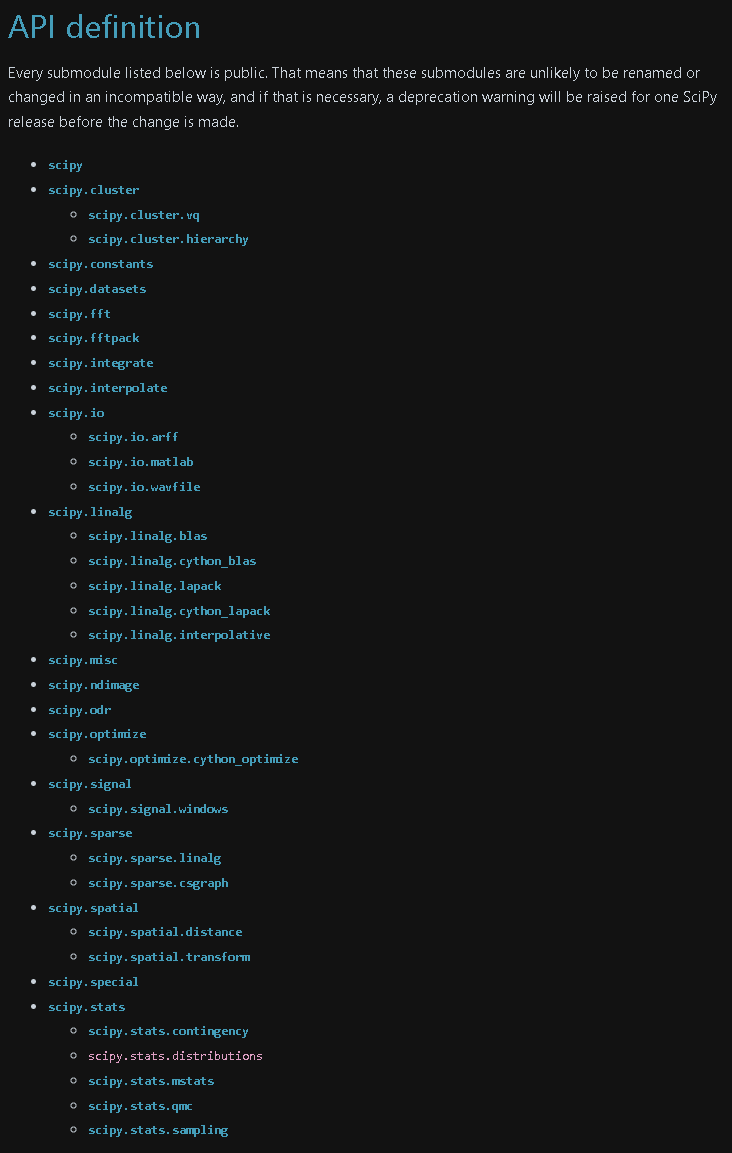
１－２．環境構築

　通常は下記のみでインストール可能だと思います。

[Terminal]
pip install scipy

　Anacondaを使用しているのであれば環境構築は不要です。Anacondaのインストール方法は下記に記載してます。

２．線形代数：linalg

　scipy.linalgでは線形代数計算が可能であり、下記のようなことが出来ます。今回は基礎的な内容のみ紹介します。

Basic（基本操作）
Eigenvalue Problems（一般化固有値問題）
Decompositions（分解）
Matrix Functions（マトリックス関数）
Matrix Equation Solvers（ソルバー）
Sketches and Random Projections
Special Matrices
Low-level routines

２－１．基本操作

　線形代数の簡単な操作を紹介します。なお同様の操作はNumpyでも可能です。線形代数の詳細な説明はNumpyの記事に記載済みのため、ここではAPIのみ紹介します。

逆行列：scipy.linalg.inv
　逆行列（元の内積が単位行列となる）を計算

[API]
scipy.linalg.inv(a, overwrite_a=False, check_finite=True)

[IN]
import numpy as np
from scipy import linalg
a = np.array([[1., 2.], [3., 4.]])
a_inv = linalg.inv(a) # 逆行列

display(a, a_inv, a @ a_inv) # 行列積

[OUT]
array([[1., 2.],
       [3., 4.]])

array([[-2. ,  1. ],
       [ 1.5, -0.5]])

array([[1.0000000e+00, 0.0000000e+00],
       [8.8817842e-16, 1.0000000e+00]])

上三角行列・下三角行列：triu(), tril()
　Version1.11.0では非推奨となり、numpyを使用することが推奨

[API]
scipy.linalg.tril(m, k=0)
scipy.linalg.triu(m, k=0)

[IN]
import numpy as np
from scipy import linalg

a = np.array([[1., 2., 3.], 
              [4., 5., 6.],
              [7., 8., 9.],
              [10., 11., 12.]])

a_triu = linalg.triu(a)
a_tril = linalg.tril(a)

display(a_triu, a_tril)

[OUT]
array([[1., 2., 3.],
       [0., 5., 6.],
       [0., 0., 9.],
       [0., 0., 0.]])

array([[ 1.,  0.,  0.],
       [ 4.,  5.,  0.],
       [ 7.,  8.,  9.],
       [10., 11., 12.]])

行列式：det

[API]
scipy.linalg.det(a, overwrite_a=False, check_finite=True)

[IN]
import numpy as np
from scipy import linalg

a = np.array([[1., 7., 2., 4.], 
              [1., 5., 2., 4.], 
              [3., 0., 1., 0.], 
              [2., 1., 5., -3.]])

a_det = linalg.det(a)
a_det

[OUT]
-134.00000000000006

連立方程式：solve
　連立方程式を解く。例としてa@x=bにおけるxを行列計算を用いて計算

$$
x_1+2x_2=5 \\
3x_1+4x_2=6
$$

[API]
scipy.linalg.solve(a, b, lower=False, overwrite_a=False, 
                   overwrite_b=False, check_finite=True, 
                   assume_a='gen', transposed=False)

[IN]
a = np.array([[1, 2],
              [3, 4]])
b = np.array([5, 6])

x = linalg.solve(a, b)
x

[OUT]
array([-4. ,  4.5])

３．数値積分：integrate

　scipy.integrateでは数値積分計算が可能です。今回は基礎的な内容のみ紹介します。

３－１．積分のエリア計算：quad

　関数や分布とx軸の間の面積、つまり積分計算は”integrate.quad(<関数>, <積分下限>, <積分上限>, args=(<関数の引数>))”で計算できます。
　出力は値と絶対誤差となります。

[API]
scipy.integrate.quad(func, a, b, args=(), full_output=0, 
                     epsabs=1.49e-08, epsrel=1.49e-08, limit=50, 
                     points=None, weight=None, wvar=None, 
                     wopts=None, maxp1=50, limlst=50, 
                     complex_func=False)

　まずは積分範囲を有限として計算した結果は下記の通りです。参考までにExcelで検算しています。

[IN]
from scipy import integrate
import numpy as np
x2 = lambda x: x**2
area, error = integrate.quad(x2, 0, 4)
print(f'area: {area:.3f}, error: {error}')

[OUT]
area: 21.333, error: 2.368475785867001e-13

　積分範囲を無限にすることも可能です。標準正規分布の平均値から無限大に積分すると0.5となり、同じ結果を得られていることを確認できました。

[IN]
def gaussian_distribution(x, mu, sigma):
    return 1 / (np.sqrt(2 * np.pi) * sigma) * np.exp(-((x - mu) / sigma)**2 / 2)

area, error = integrate.quad(gaussian_distribution, 0, np.inf, args=(0, 1))
print(f'area: {area:.3f}, error: {error}')

[OUT]
area: 0.500, error: 5.08909572043076e-09

４．疎行列：sparse

　疎行列（Sparse Matrix）とは、ほとんどの要素がゼロである行列のことを指します。これらは、例えば機械学習でのOne-Hotエンコーディングなどでよく見られます。このような行列はメモリを効率的に使用するために特殊な形式で保存されます。

　疎行列は一般的な行列と同じように扱うことができますが、その内部のデータ構造は全く異なります。一般的に疎行列は非ゼロ要素の値とその位置情報だけを保存するため、大量のゼロ要素を省略することでメモリの使用量を大幅に削減します。疎行列を操作する際の算術演算子は、この特殊なデータ構造を利用して高速化されており、一部の演算では通常の密行列よりも疎行列の方が高速に計算できる場合があります。

　Scipyでは”scipy.sparse”で疎行列を取り扱いCOO形式、CSR形式、CSC形式、LIL形式といったさまざまな形式の疎行列をサポートしています。

COO形式（Coordinate format）：非ゼロ要素の値とそれぞれの位置を保存します。疎行列を作成する際には高速で、CSR/CSC形式への変換も高速です。
CSR形式（Compressed Sparse Row format）：行方向に圧縮した疎行列を保存します。行に対する高速なスライシングや算術演算、行ベクトルとの高速な積をサポートします。
CSC形式（Compressed Sparse Column format）：列方向に圧縮した疎行列を保存します。列に対する高速なスライシングや算術演算、列ベクトルとの高速な積をサポートします。
LIL形式（List of Lists format）：行ごとに非ゼロ要素をリストで保存します。疎行列の構造を動的に変更する際に便利です。

４－１．COO方式(座標形式)：coo_matrix

　COO形式（Coordinate format）では、非ゼロデータとそれぞれのデータの行列位置（行と列のインデックス）を記録します。これにより、大量のゼロ要素を持つ行列を効率よく表現することができます。

[API]
class scipy.sparse.coo_matrix(arg1, shape=None, dtype=None, copy=False)

　Scipyでは、"scipy.sparse.coo_matrix"というクラスを用いてCOO形式の疎行列を取り扱います。出力からわかるように非ゼロデータは指定された行列位置に配置され、残りの部分はすべて0で埋められています。

[IN]
import numpy as np
from scipy.sparse import coo_matrix

# 非ゼロデータ
data = np.array([4, 5, 7, 9])

# データの行列位置
row = np.array([0, 3, 1, 0])
col = np.array([0, 3, 1, 2])

# COO形式スパースマトリックスの作成
matrix = coo_matrix((data, (row, col)), shape=(4, 4))
print(matrix)

# データの確認
print(matrix.toarray())

[OUT]
  (0, 0)	4
  (3, 3)	5
  (1, 1)	7
  (0, 2)	9

[[4 0 9 0]
 [0 7 0 0]
 [0 0 0 0]
 [0 0 0 5]]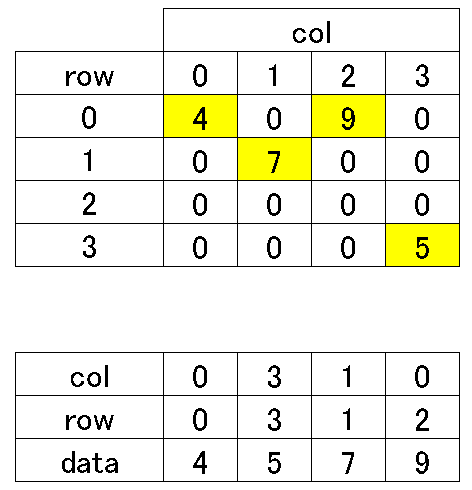

４－２．圧縮行格納方式(CSR方式)：csr_matrix

　圧縮行格納方式(Compressed Sparse Row)では、非ゼロデータと各行の非ゼロデータの開始位置を示すポインタ、それぞれのデータの列インデックスを記録します。CSR形式は行のスライス操作（特定の行を抽出する操作）が効率的に行えるため、行の操作が多い場合にはCSR形式が適しています。

[API]
class scipy.sparse.csr_matrix(arg1, shape=None, dtype=None, copy=False)

　Scipyでは、"scipy.sparse.csr_matrix"というクラスを用いてCSR形式の疎行列を取り扱います。CSR形式では、スパース行列を3つの一次元配列で表現します。

values（非ゼロ要素）: スパース行列の非ゼロ要素を左上から右下に向かって行ごとに読み込みます。
column_indices（列インデックス：indices）: 各非ゼロ要素の列インデックスを保持します。
row_pointers（行ポインタ：indptr）: valuesとcolumn_indices配列における各行の開始位置を示します。

　行ポインタを理解するために例題２つ及び選択方式を図式化しました。

[IN]
import numpy as np
from scipy.sparse import csr_matrix

# 非ゼロデータと列インデックス
data = np.array([4, 9, 7, 5]) # 非ゼロデータ
indices = np.array([0, 2, 1, 3]) #列方向のindex

# 非ゼロデータの開始位置を示すポインタ
indptr = np.array([0, 2, 3, 3, 4])

# CSR形式スパースマトリックスの作成
matrix = csr_matrix((data, indices, indptr), shape=(4, 4))

# データの確認
print(matrix)
print(matrix.toarray())

[OUT]
  (0, 0)	4
  (0, 2)	9
  (1, 1)	7
  (3, 3)	5


[[4 0 9 0]
 [0 7 0 0]
 [0 0 0 0]
 [0 0 0 5]]

[IN]
# 非ゼロデータと列インデックス
data = np.array([1, 2, 3, 4, 5])
indices = np.array([2, 0, 3, 0, 2])

# 非ゼロデータの開始位置を示すポインタ
indptr = np.array([0, 1, 3, 3, 5])

# CSR形式スパースマトリックスの作成
matrix = csr_matrix((data, indices, indptr), shape=(4, 4))

# データの確認
print(matrix)
print(matrix.toarray())

[OUT]
  (0, 2)	1
  (1, 0)	2
  (1, 3)	3
  (3, 0)	4
  (3, 2)	5


[[0 0 1 0]
 [2 0 0 3]
 [0 0 0 0]
 [4 0 5 0]]

【コラム：CSR方式をCOO構造で作成】
　CSRの構造を理解するのが難しい場合、COOと同じ引数（行列のIndex）を与えても同様の行列を作成できます。なおこの時のデータはCSR方式で保持されます。

[IN]
# 非ゼロデータ
data = np.array([4, 5, 7, 9])

# データの行列位置
row = np.array([0, 3, 1, 0])
col = np.array([0, 3, 1, 2])

matrix_coo = coo_matrix((data, (row, col)), shape=(4, 4))
matrix_csr = csr_matrix((data, (row, col)), shape=(4, 4))

display(matrix_coo)
print(matrix_coo)
print(matrix_coo.toarray())
display(matrix_csr)
print(matrix_csr)
print(matrix_csr.toarray())

[OUT]
<4x4 sparse matrix of type '<class 'numpy.int32'>'
	with 4 stored elements in COOrdinate format>
  (0, 0)	4
  (3, 3)	5
  (1, 1)	7
  (0, 2)	9
[[4 0 9 0]
 [0 7 0 0]
 [0 0 0 0]
 [0 0 0 5]]


<4x4 sparse matrix of type '<class 'numpy.intc'>'
	with 4 stored elements in Compressed Sparse Row format>
  (0, 0)	4
  (0, 2)	9
  (1, 1)	7
  (3, 3)	5
[[4 0 9 0]
 [0 7 0 0]
 [0 0 0 0]
 [0 0 0 5]]

４－３．圧縮列格納方式(CSC方式)：csc_matrix

　圧縮列格納方式(Compressed Sparse Column: CSC)はCSR方式と非常に似ており、ポインタが列方向になります。よって、列のスライス操作が効率的に行えるため、列の操作が多い場合にはCSC形式が適しています。

values（非ゼロ要素）: スパース行列の非ゼロ要素を左上から右下に向かって行ごとに読み込みます。
row_indices（行インデックス：indices）: 各非ゼロ要素の列インデックスを保持します。
column_pointers（列ポインタ：indptr）: valuesとcolumn_indices配列における各行の開始位置を示します。

[API]
class scipy.sparse.csc_matrix(arg1, shape=None, dtype=None, copy=False)

　Scipyでは、"scipy.sparse.csc_matrix"というクラスを用いてCSC形式の疎行列を取り扱います。

[IN]
import numpy as np
from scipy.sparse import csc_matrix

# 非ゼロデータと行インデックス
data = np.array([4, 9, 7, 5])
indices = np.array([0, 0, 1, 3])

# 非ゼロデータの開始位置を示すポインタ
indptr = np.array([0, 1, 1, 2, 4])

# CSC形式スパースマトリックスの作成
matrix = csc_matrix((data, indices, indptr), shape=(4, 4))

# データの確認
print(matrix.toarray())

[OUT]
[[4 0 9 0]
 [0 0 0 7]
 [0 0 0 0]
 [0 0 0 5]]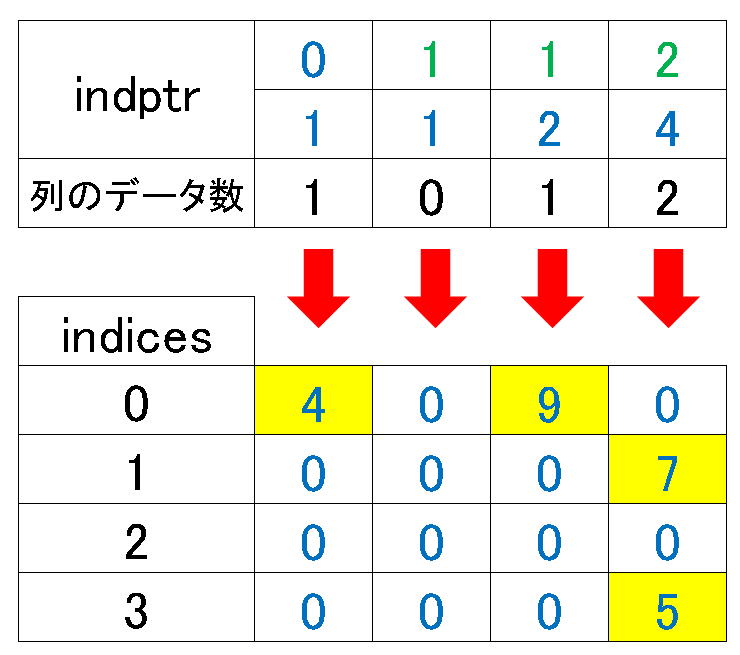

４－４．lil_matrix

　LIL (List of Lists) 形式は、Pythonのリストを2次元配列として使用し、スパース行列を表現します。これは各行が自身のリストを持ち、そのリスト内に非ゼロ値とその位置（インデックス）の情報を保持する形式です。PythonのListと異なり非ゼロデータ情報のみ持つため効率的です。

　CSR形式とLIL形式を比較すると、両者ともスパース行列を効率的に格納するための形式ですが、それぞれ異なる種類の操作に対して最適化されています。

LIL形式：要素の追加や変更といった動的な操作に対して効率的です。LIL形式の行列に新たな要素を追加する際には、リストの末尾に新たな要素を追加するだけで良く操作が容易で計算コストも小さいです。
CSR形式：行列の演算（例えば行列同士の積）や行全体を対象とした操作（例えば特定の行を抽出する）に対して効率的です。しかし、CSR形式の行列に新たな要素を追加する際には、全体のデータ構造を更新する必要があるため、計算コストが大きくなります。

[API]
class scipy.sparse.lil_matrix(arg1, shape=None, dtype=None, copy=False)

　Scipyでは、"scipy.sparse.lil_matrix"というクラスを用いてLIL形式の疎行列を取り扱います。結果から下記が確認できます。

LIL形式はPythonのリストのように扱えるため理解しやすい
LIL形式は非ゼロデータのみ情報を保持しているため効率がよい
tocsr()でCSR方式に変換が簡単に可能：処理に合わせて変換

[IN]
from scipy.sparse import lil_matrix, csr_matrix

# Initialize a 4x4 LIL matrix
lil_mat = lil_matrix((4, 4), dtype=int)
print(type(lil_mat), lil_mat.shape)
print(f'{"#"*15}初期化：LIL matrix{"#"*15}')
print(lil_mat.toarray())

# Add values to the LIL matrix
lil_mat[0, 2] = 3
lil_mat[1, 0] = 2
lil_mat[1, 3] = 3
lil_mat[3, 0] = 1
lil_mat[3, 2] = 1

print(f'{"#"*15}LIL matrixのデータ保持情報{"#"*15}')
print(lil_mat)
print(f'{"#"*15}LIL matrix配列{"#"*15}')
print(lil_mat.toarray())

# Convert LIL matrix to CSR format
csr_mat = lil_mat.tocsr()

print(f'{"#"*15}CSRのデータ保持情報{"#"*15}')
print(csr_mat)
print(f'{"#"*15}CSR matrix配列{"#"*15}')
print(csr_mat.toarray())

[OUT]
<class 'scipy.sparse.lil.lil_matrix'> (4, 4)
###############初期化：LIL matrix###############
[[0 0 0 0]
 [0 0 0 0]
 [0 0 0 0]
 [0 0 0 0]]
###############LIL matrixのデータ保持情報###############
  (0, 2)	3
  (1, 0)	2
  (1, 3)	3
  (3, 0)	1
  (3, 2)	1
###############LIL matrix配列###############
[[0 0 3 0]
 [2 0 0 3]
 [0 0 0 0]
 [1 0 1 0]]
###############CSRのデータ保持情報###############
  (0, 2)	3
  (1, 0)	2
  (1, 3)	3
  (3, 0)	1
  (3, 2)	1
###############CSR matrix配列###############
[[0 0 3 0]
 [2 0 0 3]
 [0 0 0 0]
 [1 0 1 0]]

５．最適化：optimization

　scipy.optimizationでは目的関数の最小化／最大化の最適化を計算します。Excelでいうソルバーのようなものです。
　Scipyでは様々な最適化手法が実装されているため用途に合ったものを選択します。

Optimization
- Local (multivariate) optimization
- Global optimization
Least-squares and curve fitting
- Nonlinear least-squares
- Linear least-squares
- Curve fitting
Root finding
- Scalar functions
- Multidimensional
Linear programming / MILP
Assignment problems

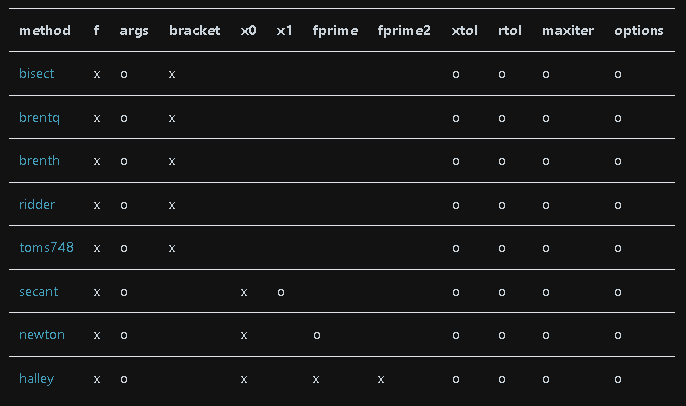
５－１．最適化手法の選択：root_scalar

　自分で最適化手法（ソルバー）を選択できるものとして"root_scalar"があります。具体的なソルバー(method)は下記の通りです(x:必須, 〇:任意)。
　デフォルトでは状況に応じた最適なソルバーが使用されますが、結果の解釈を高めるならソルバーは自分で選択する方がベターと思います。

[API]
scipy.optimize.root_scalar(f, args=(), method=None, bracket=None, 
                           fprime=None, fprime2=None, x0=None, x1=None, 
                           xtol=None, rtol=None, maxiter=None, options=None)

　５－１－１．ニュートン・ラフソン法

　"scipy.optimize.root_scalar"のmethodに'newton'を渡すことでニュートン・ラフソン法が使用できます。ニュートン法では関数f(x)において、f(x)=0となるxを数値計算で求めることが出来ます。原理としては、①f(x)の微分によりx軸との交点から近似値を算出、②計算条件を満たしているか判定　を繰り返し計算することで真値に近づけていきます。

[API]
scipy.optimize.root_scalar(f, args=(), method=None, bracket=None, 
                           fprime=None, fprime2=None, 
                           x0=None, x1=None, xtol=None, 
                           rtol=None, maxiter=None, options=None)

[IN]
from scipy.optimize import root_scalar

#関数f(x)
def f(x):
    return (x+2)**2 - 10

def numeriacal_diff_f(x):
    h = 1e-4 #0.0001
    return (f(x+h) - f(x-h)) / (2*h)

solver = root_scalar(f, fprime=numeriacal_diff_f, method='newton', x0=8)
print(solver)

[OUT]
      converged: True
           flag: 'converged'
 function_calls: 12
     iterations: 6
           root: 1.1622776601683795

５－２．最小化：minimize

　”scipy.optimize.minimize”では設定した目的関数(fun)を最小化する入力値を探索します。

[API]
scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, 
                        hessp=None, bounds=None, constraints=(), tol=None, 
                        callback=None, options=None)

　サンプルコードは下記記事を参考にさせていただきました。minimize()に関数と初期値を渡すことで最小解を取得できることを確認しました。

【目的関数】

$$
f(x)=-x^2+x^4
$$

【導関数（微分）による最適解】

$$
f'(x)=-2x+4x^3=2x(2x^2-1)より\\
極値x_0=0 , x_\pm =\pm \frac{1}{\sqrt{2}}
$$

[IN]
import numpy as np
import matplotlib.pyplot as plt 

def f(x):
    y = - x**2 + x**4
    return y

x = np.linspace(-1.5, 1.5, 60)
y = f(x)
sns.lineplot(x, y, label='f(x)')

from scipy.optimize import minimize
x_init = 1.0
print(minimize(f, x_init))
x_min = minimize(f, x_init).x
y_min = f(x_min)
sns.scatterplot(x_min, y_min, label='minimize', color='red')

[OUT]
      fun: -0.2499999999998436
 hess_inv: array([[0.24908438]])
      jac: array([-1.09151006e-06])
  message: 'Optimization terminated successfully.'
     nfev: 14
      nit: 5
     njev: 7
   status: 0
  success: True
        x: array([0.7071065])

６．統計：stats - 正規分布

　scipy.statsでは確率分布や頻度統計、検定など多数の機能が実装されています。なお統計の基礎は別記事で紹介しています。

　統計学は基礎学問であり範囲が広いためScipyですべてカバーされておりません。Scipyを補間するものとして下記が紹介されています。

statsmodels: 回帰、線形モデル、時系列分析（scipy.statsでもカバー）
Pandas: 表データ、時系列機能、他の統計言語とのインタフェース
PyMC: ベイズ統計モデリング、確率的機械学習
scikit-learn: 分類、回帰、モデル選択
Seaborn: 統計データの可視化
rpy2: PythonからRへのブリッジ

　本章では確率分布について紹介します。確率分布は紹介済みのため実装のみ説明します。

　まず初めにグラフの可視化が見やすいように関数を作成しておきます。

[IN]
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import scipy
from scipy import stats

def plot_distribution(ax, x, y, title, xlabel:str, ylabel:str, label:str=None, color:str=None, save:bool=False, addvalue:bool=False):
    if color is None: color='blue'
    
    ax.plot(x, y, color=color, label=label)
    ax.set(xlabel=xlabel, ylabel=ylabel, ylim=(0, 1.1*max(y)))
    plt.title(title, y=-0.15)
    if addvalue:
        for idx, (x_, y_) in enumerate(zip(x, y)):
            y_adjuster = max(y) * 0.01
            if idx % 5 == 0:
                ax.text(x_, y_+y_adjuster, f'({x_:.2f}, {y_:.3f})', fontsize=8)
            
    ax.grid(), ax.legend()
    if save:
        plt.savefig(f'./{title}.png')
    

[OUT]

６－１．正規分布：norm

　正規分布（下記式）は”scipy.stats.norm”で実装します。

$$
\mathcal{N}(\mu, \sigma^2)=\dfrac{1}{\sqrt{2\pi\sigma^2}}\exp(-\dfrac{(x-\mu)^ 2}{2\sigma^ 2})
$$

　メソッド及び引数でよく使用するものは下記の通りです。オブジェクト化した変数にメソッドを使用してもよいですが、本記事では基本的には直接メソッドを記載していきます。

[API]
scipy.stats.norm = <scipy.stats._continuous_distns.norm_gen object>

[IN]
from scipy import stats

#オブジェクト確認
norm_ojb = stats.norm(loc=0, scale=1) #平均0, 標準偏差1の標準正規分布
print(norm_ojb)

[OUT]
<scipy.stats._distn_infrastructure.rv_frozen object at 0x00000277C834A430>

【引数】
　●loc(location)：平均値
　●scale：標準偏差

【メソッド・属性】
　●pdf(probability density function)：確率密度関数
　●cdf(Cumulative distribution function)：累積分布関数
　　➡確率密度関数をデータ方向に総和していく分布
　　➡確率分布の総面積は1のため、cdfの最大値も1となる

　６－１－１．正規分布の確率密度分布：norm.pdf

　正規分布の確率密度分布のデータは"stats.norm.pdf(x)"で作成します。出力値はNumpy配列となります。データ(x)をNumpy配列で渡せば同じサイズの確率密度が出力されます。

[IN]
#標準正規分布
fig, ax = plt.subplots(figsize=(8, 6), facecolor='white')
    
x = np.linspace(-4, 4, 100)
y = stats.norm(loc=0, scale=1).pdf(x)
print(f'xデータ型: {type(x)}, xデータ形状: {x.shape}, yデータ型: {type(y)}, yデータ形状: {y.shape}')
plot_distribution(ax, x, y, r'標準正規分布$\mathcal{N}(0, 1)$', 'x', 'y', save=False, addvalue=True)

[OUT]
xデータ型: <class 'numpy.ndarray'>, xデータ形状: (100,), yデータ型: <class 'numpy.ndarray'>, yデータ形状: (100,)

　データ1個で渡せばその点における確率密度が出力されます。

[IN]
y_0 = stats.norm(loc=0, scale=1).pdf(0)
y_125 = stats.norm(loc=0, scale=1).pdf(1.25)
y_246 = stats.norm(loc=0, scale=1).pdf(2.46)

print(f'P(y|x=0)= {y_0:.3f}')
print(f'P(y|x=1.25)= {y_125:.3f}')
print(f'P(y|x=2.46)= {y_246:.3f}')

[OUT]
P(y|x=0)= 0.399
P(y|x=1.25)= 0.183
P(y|x=2.46)= 0.019

　下記のように様々な正規分布を作成できます。

[IN]
x = np.linspace(-10, 10, 100)
norm_dist1 = stats.norm(loc=0, scale=5).pdf(x)
norm_dist2 = stats.norm(loc=3, scale=1).pdf(x)
norm_dist3 = stats.norm(loc=-3, scale=5).pdf(x)
norm_dist4 = stats.norm(loc=8, scale=0.5).pdf(x)
norm_dist5 = stats.norm(loc=-8, scale=0.5).pdf(x)
norm_dists = [norm_dist1, norm_dist2, norm_dist3, norm_dist4, norm_dist5]

labels = [r'$\mathcal{N}(0, 5)$', r'$\mathcal{N}(3, 1)$', r'$\mathcal{N}(-3, 5)$', r'$\mathcal{N}(8, 0.5)$', r'$\mathcal{N}(-8, 0.5)$']
fig, ax = plt.subplots(figsize=(8, 6), facecolor='white')
for idx, (norm_dist, label) in enumerate(zip(norm_dists, labels)):
    plot_distribution(ax=ax, x=x, y=norm_dist, xlabel='x', ylabel='y',
                      label=label, title='標準正規分布', color=f'C{idx}', save=False, addvalue=False)
plt.show()

[OUT]

　６－１－２．複数の正規分布を同時作成

　前述の通り１点データを渡すことでその点における確率密度を計算することが出来ます。"stats.norm"に配列で下記を渡すことでそれぞれの正規分布における確率密度が計算できます。
　つまり尤度の計算ができ、最尤推定やベイズ推定が可能となります。

平均値：正規分布の中心
標準偏差：正規分布の広がり
データ：正規分布$${f(x)}$$における$${x}$$、つまり確率変数$${x}$$

【計算式】
　平均値$${\mu}$$と標準偏差$${\sigma}$$を指定すると正規分布が作成できます。その正規分布に対して確率変数$${x}$$を渡すことで確率密度が計算できます。
　該当する正規分布を条件付き確率で表し、複数の正規分布を表現するためにベクトルとして平均ベクトル$${\bf \mu}$$, 標準偏差ベクトル$${\bf \sigma}$$、データ（確率変数）$${\bf X}$$を用いると正規分布は下記の通り表現できます。

$$
X =\begin{bmatrix}x_1\\
x_2\\ \vdots \\x_n
\end{bmatrix},
\quad
\mu =\begin{bmatrix}
\mu_1\\\mu_2\\\vdots\\
\mu_n\end{bmatrix},
\quad
\sigma =\begin{bmatrix}\sigma_1\\\sigma_2\\\vdots\\\sigma_n\end{bmatrix}
$$

$$
\begin{aligned} \mathcal{N}_1(x_1|\mu_1, \sigma_1^2)
& =\dfrac{1}{\sqrt{2\pi\sigma_1^2}}\exp\left(-\dfrac{(x_1-\mu_1)^ 2}{2\sigma_1^ 2}\right)\\ \mathcal{N}_2(x_2|\mu_2, \sigma_2^2)
& =\dfrac{1}{\sqrt{2\pi\sigma_2^2}}\exp\left(-\dfrac{(x_2-\mu_2)^ 2}{2\sigma_2^ 2}\right)\\ \vdots & \vdots \\ \mathcal{N}_n(x_n|\mu_n, \sigma_n^2)
& =\dfrac{1}{\sqrt{2\pi\sigma_n^2}}\exp\left(-\dfrac{(x_n-\mu_n)^ 2}{2\sigma_n^ 2}\right) \end{aligned}
$$

　この確率変数$${x}$$を機械学習モデル（例：単回帰$${y=ax+b}$$）にすることで、推論値$${y}$$を中心とする正規分布における測定値の確率密度が計算でき、その総乗をとることで尤度$${L}$$が計算できます。

$$
L(a, b | \mathbf{y}, \mathbf{x}) = \prod_{i=1}^N \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(y_i - ax_i - b)^2}{2\sigma^2}\right)
$$

　詳細を理解したい人は下記記事参照のこと。

【実装編１：シンプル】
　まずは数値をそのまま当てはめてみます。各ベクトルは３つの要素を含むため、３つの正規分布におけるそれぞれの確率密度を計算しています。結果は下記の通りです。

$$
X =\begin{bmatrix}x_1\\
x_2\\ x_3\end{bmatrix}=\begin{bmatrix}0\\
1\\ 2\end{bmatrix}
,\quad
\mu=\begin{bmatrix}\mu_1\\
\mu_2\\ \mu_3\end{bmatrix} =\begin{bmatrix}
0\\ 2\\ 4\end{bmatrix},\quad
\sigma=\begin{bmatrix}\sigma_1\\
\sigma_2\\ \sigma_3\end{bmatrix} =\begin{bmatrix} 1\\ 1\\ 1\end{bmatrix}
$$

$$
\begin{aligned}
\mathcal{N}_1(x_1|\mu_1, \sigma_1^2)
& =\dfrac{1}{\sqrt{2\pi\sigma_1^2}}\exp\left(-\dfrac{(x_1-\mu_1)^ 2}{2\sigma_1^ 2}\right)\\ \mathcal{N}_2(x_2|\mu_2, \sigma_2^2)
& =\dfrac{1}{\sqrt{2\pi\sigma_2^2}}\exp\left(-\dfrac{(x_2-\mu_2)^ 2}{2\sigma_2^ 2}\right)\\
\mathcal{N}_n(x_3|\mu_3, \sigma_3^2)
& =\dfrac{1}{\sqrt{2\pi\sigma_3^2}}\exp\left(-\dfrac{(x_3-\mu_3)^ 2}{2\sigma_3^ 2}\right) \end{aligned}
$$

[IN] #正規分布 
x = np.array([0, 1, 2])
vec_mean = [0, 2, 4]
vec_sigma = [1, 1, 1]
y = stats.norm(loc=vec_mean, scale=vec_sigma).pdf(x)
y

[OUT]
array([0.39894228, 0.24197072, 0.05399097])

【実装編２：応用編（尤度の計算）】
　応用へとして尤度を計算してみます。この尤度を最大化するのが最尤推定であり単回帰にも応用できます。単回帰での詳細は下記記事に参照。

　まずはサンプルデータを作成します。

[IN]
x = np.array([0.0148, 0.0078, 0.0844, 0.1290, 0.0295, 0.0791, 0.0181, 0.0734])
y = np.array([311., 122., 243., 248.,  91., 281., 142., 295.])
df = pd.DataFrame({'x':x, 'y':y})
df.plot.scatter(x='x', y='y', figsize=(6, 4), facecolor='white')

[OUT]

　次に機械学習モデルで最適なパラメータ（傾きと切片）を求めます。最適化には"stats.linregress"を使用しました。

　このパラメータは最大の尤度をもつ値であるため、別の値を入力すれば後で計算する尤度は小さくなります。

[IN]
#２．線形回帰（機械学習）
slope, intercept, r_value, p_value, std_err = stats.linregress(x, targets)
y_pred = slope * x + intercept
print(f'傾き：{slope:.3f}, 切片：{intercept:.3f}, 相関係数r：{r_value:.3f}, p値：{p_value:.3f}, 標準誤差：{std_err:.3f}')
plt.plot(x, y_pred, color='red')

[OUT]
傾き：970.006, 切片：163.748, 相関係数r：0.491, p値：0.217, 標準誤差：702.585

　次に計算した推論値$${\hat y}$$を中心とする正規分布を"stats.norm
(loc=y_pred, scale=100)"で作成しました。分散は最適な選定が必要ですが、今回は確率密度の値が見えやすいように大きな値で設定しました。このオブジェクト内には渡したデータと同じ数の正規分布を持ちます。

　そのオブジェクトに確率密度関数(pdf)で目的変数（ラベル値）を渡すことで推論値に対する各データの確率密度が計算でき、各確率密度を総乗すると尤度になります。これを式でまとめると下記の通りです。

$$
L(a, b | \mathbf{y}, \mathbf{x}) = \prod_{i=1}^N \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(y_i - (ax_i - b))^2}{2\sigma^2}\right)
$$

[IN]
# ３．各データ点に対する正規分布
norm_dists = stats.norm(loc=y_pred, scale=100) #推論値yを平均（中心）とする正規分布
print(norm_dists)

# ４．尤度の計算
prob_density = norm_dists.pdf(targets)
print(prob_density)
likelihood = np.prod(prob_density)
print(f'尤度：{likelihood:.3e}')

[OUT]
<scipy.stats._distn_infrastructure.rv_frozen object at 0x000001D74B6A0790>

[0.00164967 0.00353267 0.00398806 0.00366964 0.00238674 0.00367493
 0.00369287 0.00333117]

尤度：9.202e-21

　計算結果を見てわかる通り、正規分布の最大値<1であり総乗するため尤度は非常に小さな値となりアンダーフローの問題が生じます。そのため尤度関数にlogを取り対数尤度関数に変更することでこの問題を解決できます。

$$
\begin{aligned}
\ln L(a, b | \mathbf{y}, \mathbf{x})
&= \ln\left( \prod_{i=1}^N \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(y_i - (ax_i - b))^2}{2\sigma^2}\right)\right)\\
&= \sum_{i=1}^N \left[ -\frac{1}{2}\ln(2\pi\sigma^2) -\frac{(y_i - (ax_i - b))^ 2}{2\sigma^ 2} \right]\\
&= -\frac{N}{2} \ln(2\pi\sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^N (y_i - (ax_i + b))^2
\end{aligned}
$$

[IN]
log_prob_density = np.log(prob_density)
print(log_prob_density)
log_likelihood = np.sum(log_prob_density)
print(f'対数尤度：{log_likelihood:.3e}')

[OUT]
[-6.40718077 -5.6457003  -5.5244509  -5.60766051 -6.03782887 -5.60622243
 -5.60135155 -5.70443296]
対数尤度：-4.613e+01

　上記よりパラメータ（傾きと切片）に対する尤度（確率密度の積＝データの出現のしやすさ＝尤もらしさ）を計算できました。パラメータと尤度をプロットすると分布が得られ、この尤度を最大化するのが最尤推定です。

[IN]
slopes = np.linspace(0, 2000, 100)
intercepts = np.linspace(0, 300, 100)

# 各パラメータにおける予測値と尤度を計算
likelihoods = np.zeros((len(slopes), len(intercepts)))
for i, slope in enumerate(slopes):
    for j, intercept in enumerate(intercepts):
        y_pred = slope * x + intercept
        norm_dists = stats.norm(loc=y_pred, scale=100)
        prob_density = norm_dists.pdf(targets)
        likelihood = np.prod(prob_density)
        likelihoods[j, i] = likelihood #j行i列

plt.figure(figsize=(8, 6), facecolor='white')
plt.contourf(slopes, intercepts, likelihoods, cmap='Blues')
plt.xlabel('slope'), plt.ylabel('intercept')
plt.show()

[OUT]

６－２．多変量正規分布：multivariate_normal

　多次元正規分布は”scipy.stats.multivariate_normal”で実装できます。

[API]
scipy.stats.multivariate_normal 
= <scipy.stats._multivariate.multivariate_normal_gen object>

【確率密度関数(probability density function)：pdf】
　多変量正規分布に必要な平均ベクトル$${\bf \mu}$$と分散共分散行列$${\bf \Sigma}$$を渡すとオブジェクトを作成できます。そこに各次元のデータを結合した変数を渡すことで確率密度分布を取得できます。

[API]
pdf(x, mean=None, cov=1, allow_singular=False)

[IN]
#多変量正規分布（multivariate normal distribution）
#データ
x, y = np.mgrid[-5:5:0.1, -5:5:0.1]
xy = np.dstack([x, y])
print(f'x:{x.shape}, y:{y.shape}, xy:{xy.shape}')

#２次元正規分布
vec_mu = np.array([0, 0])
vec_sigma = np.array([[1, 0], [0, 1]])

#多変量正規分布の確率密度関数
z = stats.multivariate_normal(mean=vec_mu, cov=vec_sigma)
print(z)
z = z.pdf(xy)
print(z.shape)

plt.figure(figsize=(8, 6), facecolor='white')
plt.contourf(x, y, z, cmap='Blues')

[OUT]
x:(100, 100), y:(100, 100), xy:(100, 100, 2)
<scipy.stats._multivariate.multivariate_normal_frozen object at 0x0000024F920831C0>
(100, 100)

【ランダム変数生成関数(Random Variable Sample )：rvs】
　平均ベクトル$${\mu}$$と分散共分散行列$${\Sigma}$$を指定した多変量ガウス分布からランダムにサンプリングするにはrvsメソッドを使用します。sizeを指定しなければ1サンプルのみ抽出でき、指定すれば複数の値をサンプリングできます。
　共役事前分布を使用した事後分布などに適用可能です（共役事前分布を使用しない場合はMCMCなどによるサンプリングが必要）。

[API]
rvs(mean=None, cov=1, size=1, random_state=None)

[IN]
x, y = np.mgrid[-5:5:0.1, -5:5:0.1]
xy = np.dstack([x, y])
vec_mu, vec_sigma = np.array([0, 0]), np.array([[1, 0], [0, 1]])
z = stats.multivariate_normal(mean=vec_mu, cov=vec_sigma) #中心 (0, 0)、分散共分散行列[[1, 0], [0, 1]]の2次元正規分布
 #サンプリング 
samples = z.rvs(size=10) #指定した2次元正規分布から10個のサンプルを生成 
print(samples)
print(f'サンプル形状：{samples.shape}')
 #サンプリング結果の可視化 
fig, ax = plt.subplots(figsize=(8, 6), facecolor='white')
ax.contourf(x, y, stats.multivariate_normal(mean=vec_mu, cov=vec_sigma).pdf(xy), cmap='Blues', label='pdf')
ax.scatter(samples[:, 0], samples[:, 1], color='red', label='samples', s=10)
ax.set(xlabel='x', ylabel='y', xticks=np.arange(-5, 5, 1), yticks=np.arange(-5, 5, 1))
plt.show()

[OUT]
[[-1.0856306   0.99734545]
 [ 0.2829785  -1.50629471]
 [-0.57860025  1.65143654]
 [-2.42667924 -0.42891263]
 [ 1.26593626 -0.8667404 ]
 [-0.67888615 -0.09470897]
 [ 1.49138963 -0.638902  ]
 [-0.44398196 -0.43435128]
 [ 2.20593008  2.18678609]
 [ 1.0040539   0.3861864 ]]

サンプル形状：(10, 2)

６－３．拡張版の正規分布

　Scipyは複数の正規分布を提供しており一部を紹介します。

scipy.stats.lognorm: 対数正規分布
scipy.stats.halfnorm: 半正規分布
scipy.stats.matrix_normal: 行列正規分布

　６－３－１．対数正規分布：lognorm

　対数正規分布(log-normal distribution)とは、確率変数の対数が正規分布に従う時にその確率変数が従う分布を指し、下記で定義されます。注意点として”正規分布を対数化したもの”とは全くの別物であり、対数正規分布はしっかりとした分布となります。

$$
f(x, s) = \frac{1}{sx\sqrt{2\pi}} \exp\left(-\frac{1}{2}\left(\frac{\log(x)}{s}\right)^2\right)
$$

[API]
scipy.stats.lognorm = <scipy.stats._continuous_distns.lognorm_gen object>

　確率変数$${x}$$は対数化された値になり理解しにくいため、今回は累積分布関数 (CDF：Cumulative Distribution Function)の逆関数であるパーセント点関数 (PPF)を使用しました。下記ではCDFが0.01, 0.99となる$${x}$$を取得して分布を可視化することで下記が確認できました。

対数正規分布も確率分布であり面積の総和(CDFの最大値)は1となる
形状はs(shape parameter)で決定される

[IN]
# 対数正規分布のパラメータを設定（シフトパラメータは0とする）
s = 0.954 # シェイプパラメータ
mean, var, skew, kurt = stats.lognorm.stats(s, moments='mvsk')

# 確率密度関数を描画
x_start, x_end = stats.lognorm.ppf(0.01, s), stats.lognorm.ppf(0.99, s) #xの値をパーセント点関数(PPF)から計算
print(f'x_start:{x_start:.3f}, x_end:{x_end:.3f}')
x = np.linspace(x_start, x_end, 100)
y = stats.lognorm.pdf(x, s) #確率密度関数(PDF)を計算
print(f'総面積：{np.trapz(y, x):.3f}')
fig, ax = plt.subplots(figsize=(8, 6), facecolor='white')
plot_distribution(ax, x=x, y=y, xlabel='x', ylabel='y', label='確率密度(PDF)@s=0.954', title='対数正規分布', color='blue', save=False, addvalue=False)

#参考として累積分布関数(CDF)を描画
y_cdf = stats.lognorm.cdf(x, s)
plot_distribution(ax, x=x, y=y_cdf, xlabel='x', ylabel='y', label='累積分布(CDF)', title='対数正規分布', color='red', save=False, addvalue=False)
ax.set(xticks=np.arange(0, 10, 1), yticks=np.arange(0, 1.1, 0.1), ylim=(0, 1.1))
ax.grid()
plt.show()

[OUT]
x_start:0.109, x_end:9.201
総面積：0.978

　６－３－２．半正規分布：halfnorm

　半正規分布は正規分布の非負の部分を2倍に拡大したものであり以下の通りです。

$$
f(x) = \sqrt{\frac{2}{\pi}} \exp\left(-\frac{x^2}{2}\right)
$$

[API]
scipy.stats.halfnorm = <scipy.stats._continuous_distns.halfnorm_gen object>

　半正規分布の特徴として「正規分布の非負（$${x\geqq0}$$）の部分に対して確率の合計が1になるように正規化したもの」です。よって、値が必ず非負で下限が0であることが分かっている場合などに使用します。

[IN]
#半正規分布
sigma = 1.0 #スケールパラメータ

x_start, x_end = stats.halfnorm.ppf(0.01, scale=sigma), stats.halfnorm.ppf(0.99, scale=sigma)
x = np.linspace(x_start, x_end, 100)
y = stats.halfnorm.pdf(x, scale=sigma)
print(f'総面積：{np.trapz(y, x):.3f}')

fig, ax = plt.subplots(figsize=(8, 6), facecolor='white')
plot_distribution(ax, x=x, y=y, xlabel='x', ylabel='y', label='半正規分布', title='半正規分布', color='blue', save=False, addvalue=False)

#通常の正規分布と比較
x = np.linspace(-3, 3, 100)
y = stats.norm.pdf(x, loc=0, scale=1)
plot_distribution(ax, x=x, y=y, xlabel='x', ylabel='y', label='正規分布', title='半正規分布', color='red', save=False, addvalue=False)
ax.set(xticks=np.arange(-3, 3.1, 1), yticks=np.arange(0, 1.1, 0.1), ylim=(0, 1.1)), ax.grid()
plt.show()

[OUT]
総面積：0.980

　６－３－３．行列正規分布：matrix_normal

　行列正規分布の確率密度関数は以下のように定義されます。ここで$${X}$$は観測される行列、$${M}$$は平均行列、$${U}$$は行の共分散行列、$${V}$$は列の共分散行列です。$${\mathrm{Tr}[\cdot]}$$はトレース（行列の対角要素の和）を表します。

$$
f(X | M, U, V) = \frac{1}{(2\pi)^{np/2}|U|^{n/2}|V|^{p/2}} \exp\left(-\frac{1}{2} \mathrm{Tr}\left[V^{-1}(X - M)^TU^{-1}(X - M)\right]\right)
$$

[API]
scipy.stats.matrix_normal = <scipy.stats._multivariate.matrix_normal_gen object>

７．統計：stats - 確率分布

　正規分布以外の確率分布もScipyで簡単に実装できます。詳細は下記が参考になります。

　各種確率分布の説明は下記記事をご確認ください。

７－１．一様分布：uniform

　一様分布は、特定の範囲内のすべての出来事が同じ確率で発生するという事を表します。

$$
f(x|a, b) =
\begin{cases}
\frac{1}{b - a} & \text{if } a \leq x \leq b, \
0 & \text{otherwise}.
\end{cases}
$$

[API]
scipy.stats.uniform = <scipy.stats._continuous_distns.uniform_gen object>

　Scipyでは"scipy.stats.uniform"で実装でき、引数のloc, scaleで分布の幅を設定できます。

[IN]
#一様分布
x = np.linspace(-1, 2, 1000)
y = stats.uniform.pdf(x, loc=0, scale=1.5) #0~1.5の一様分布
df = pd.DataFrame({'x':x, 'y':y})

fig, ax = plt.subplots(figsize=(8, 6), facecolor='white')
plot_distribution(ax, x=x, y=y, xlabel='x', ylabel='y', label='一様分布', title='一様分布', color='blue', save=False, addvalue=False)

[OUT]

７－２．ベルヌーイ分布：bernoulli

　ベルヌーイ分布は、ベルヌーイ分布は、二つの結果しか持たないランダムな試行（例：コイントス、あたり・はずれなど）の結果をモデル化するのに使用される確率分布です。

$$
P(X=k) = p^k(1-p)^{1-k} \text{ for } k \in {0, 1}
$$

[API]
scipy.stats.bernoulli = <scipy.stats._discrete_distns.bernoulli_gen object>

　Scipyでは"scipy.stats.bernoulli"で実装できます。xに確率変数(コイントスでの表・裏)、pに成功確率(x=1の確率)を渡すことでベルヌーイ分布を計算します。

[IN]
#ベルヌーイ分布
x = [0, 1]
y = stats.bernoulli.pmf(x, p=0.2)
print(f'x:{x}, y:{y}')
plt.bar(x, y, color='blue')
plt.show()

[OUT]
x:[0, 1], y:[0.8 0.2]

７－３．二項分布：binom

　二項分布は、成功確率がpであるn回の独立したベルヌーイ試行で成功する回数の確率分布です。ベルヌーイ試行は前述の通り、2つの結果（「成功」または「失敗」）しかない試行のことを指します。
　下記式ではn回の試行中で成功する確率（$${p^k}$$）と失敗する確率（$${(1-p)^{n-k}}$$）を掛け合わせ、それに成功する組み合わせの数を掛けたものになります。

$$
P(X=k) = \binom{n}{k} p^k (1-p)^{n-k}
$$

$${P(X=k)}$$：k回成功する確率
$${p^k}$$：成功する確率pをk回かけたもの
$${(1-p)^{n-k}}$$：失敗する確率（1-p）を（n-k）回かけたもの

[API]
scipy.stats.binom = <scipy.stats._discrete_distns.binom_gen object>

　二項分布はscipy.stats.binomオブジェクトを使用して実装できます。xは"0から10までの全ての成功の回数"でありyはその時の確率を出力します。

[IN]
#二項分布
x = np.arange(0, 11, 1)
y = stats.binom.pmf(x, n=10, p=0.2) #10回試行、成功確率0.2の二項分布
print(y)
fig, ax = plt.subplots(figsize=(8, 6), facecolor='white')
plot_distribution(ax, x=x, y=y, xlabel='x', ylabel='y', label='二項分布', title='二項分布', color='blue', save=False, addvalue=False)
plt.show()

[OUT]
[1.07374182e-01 2.68435456e-01 3.01989888e-01 2.01326592e-01
 8.80803840e-02 2.64241152e-02 5.50502400e-03 7.86432000e-04
 7.37280000e-05 4.09600000e-06 1.02400000e-07]

７－４．ベータ分布：beta

　ベータ分布は、0から1の間の値をとる確率変数の分布で、2つの形状パラメータ（$${\alpha}$$と$${\beta}$$）によって形状が決まります。ベータ分布は確率の確率分布としてよく使われます。つまり、ある事象が発生する確率そのものがどのように分布しているかを表現します。

　ベータ分布の確率密度関数は以下の数式で表されます。形状パラメータ（$${\alpha}$$と$${\beta}$$）の値によって、ベータ分布の形状は大きく変化します。

$$
f(x|\alpha, \beta) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha, \beta)}
$$

$${x}$$：確率変数（0〜1の間の値）
$${\alpha}$$, $${\beta}$$：形状パラメータ
$${B(\alpha, \beta)}$$：ベータ関数（確率を1にする正規化定数）

[API]
scipy.stats.beta = <scipy.stats._continuous_distns.beta_gen object>

　ベータ分布はscipy.stats.betaオブジェクトを使用して実装できます。

[IN]
#ベータ分布
x = np.linspace(0.01, 0.99, 100) #xの値は必ず0~1の間※x軸は確率
#パラメータを設定
alpha1, beta1 = 1, 1
alpha2, beta2 = 2, 2
alpha3, beta3 = 2, 5
alpha4, beta4 = 5, 2
alpha5, beta5 = 0.5, 0.5
alpha6, beta6 = 10, 2

y1 = stats.beta.pdf(x, alpha1, beta1)
y2, y3, y4, y5, y6 = stats.beta.pdf(x, alpha2, beta2), stats.beta.pdf(x, alpha3, beta3), stats.beta.pdf(x, alpha4, beta4), stats.beta.pdf(x, alpha5, beta5), stats.beta.pdf(x, alpha6, beta6)
colors = ['blue', 'red', 'green', 'orange', 'purple', 'brown']
#プロット
alphas, betas, ys = [alpha1, alpha2, alpha3, alpha4, alpha5, alpha6], [beta1, beta2, beta3, beta4, beta5, beta6], [y1, y2, y3, y4, y5, y6]
fig, ax = plt.subplots(figsize=(8, 6), facecolor='white')
for alpha, beta, color, y in zip(alphas, betas, colors, ys):
    plot_distribution(ax, x=x, y=y, xlabel='x', ylabel='y', label=f'α:{alpha}, β:{beta}', 
                      title='ベータ分布', color=color, save=False, addvalue=False)
ax.set(xticks=np.arange(0, 1.1, 0.1), yticks=np.arange(0, 4.1, 0.5), ylim=(0, 4.1)), ax.grid()
plt.show()

[OUT]

７－５．ポアソン分布：poisson

　ポアソン分布は一定の平均率でランダムに発生するイベントの確率を表す確率分布です。例えば、単位時間あたりに平均$${\lambda}$$回起こるイベントが単位時間内にk回発生する確率を表現します。

$$
P(X=k) = \frac{\lambda^k e^{-\lambda}}{k!}
$$

$${P(X=k)}$$：k回イベントが発生する確率
$${\lambda}$$：平均発生率（期待値）
$${k!}$$：kの階乗

[API]
scipy.stats.poisson = <scipy.stats._discrete_distns.poisson_gen object>

　ポアソン分布はscipy.stats.poissonオブジェクトを使用して実装できます。ここでは、単位時間あたりに平均5回のイベントが発生するという条件でポアソン分布を計算しています（xはイベント発生回数）。

[IN]
#ポアソン分布
x = np.arange(0, 21, 1)
y = stats.poisson.pmf(x, mu=5) #平均5のポアソン分布
fig, ax = plt.subplots(figsize=(8, 6), facecolor='white')
plot_distribution(ax, x=x, y=y, xlabel='x', ylabel='y', label='ポアソン分布', title='ポアソン分布', color='blue', save=False, addvalue=False)
plt.show()

[OUT]

７－６．ガンマ分布：gamma

　ガンマ分布は連続確率分布で待ち時間のモデル（ある特定のイベントが発生するまでの時間：装置の故障など）としてよく使用されます。特に、連続的な時間間隔や待ち時間のモデルによく使われます。

$$
f(x|\alpha, \beta) = \frac{\beta^{\alpha} x^{\alpha-1} e^{-\beta x}}{\Gamma(\alpha)}
$$

$${f(x|\alpha, \beta)}$$：ガンマ分布の確率密度関数
$${\alpha}$$：形状パラメータ
$${\beta}$$：尺度パラメータ
$${\Gamma(\alpha)}$$：ガンマ関数

[API]
scipy.stats.gamma = <scipy.stats._continuous_distns.gamma_gen object>

　ガンマ分布はscipy.stats.gammaオブジェクトを使用して実装できます。

[IN]
#ガンマ分布
x = np.linspace(0, 20, 100)
y = stats.gamma.pdf(x, a=1, scale=1) #a=1, scale=1のガンマ分布
fig, ax = plt.subplots(figsize=(8, 6), facecolor='white')
plot_distribution(ax, x=x, y=y, xlabel='x', ylabel='y', label='ガンマ分布', title='ガンマ分布', color='blue', save=False, addvalue=False)
plt.show()

[OUT]

７－７．指数分布：expon

　指数分布は一定の平均時間間隔で発生するイベントの間の時間をモデル化するのによく使用されます。例えば、ある装置が故障するまでの時間や、公共交通機関の到着間隔などを表現するのに用いられます。

$$
f(x|\lambda) = \lambda e^{-\lambda x}
$$

　指数分布の特徴的な点はメモリレス性（無記憶性）です。つまりある時間点までにイベントが発生しなかった場合、それが次に発生するまでの時間分布は最初からその時間が経過していない場合と同じです。これは、常に一定のレートでイベントがランダムに発生するプロセスをモデル化するのに非常に便利な特性です。

[API]
scipy.stats.expon = <scipy.stats._continuous_distns.expon_gen object>

　指数分布はscipy.stats.exponオブジェクトを使用して実装できます。このコードではλ=1.0（平均発生間隔が1.0）の指数分布をプロットしています.

[IN]
#ガンマ分布
x = np.linspace(0, 20, 100)
y = stats.gamma.pdf(x, a=1, scale=1) #a=1, scale=1のガンマ分布
fig, ax = plt.subplots(figsize=(8, 6), facecolor='white')
plot_distribution(ax, x=x, y=y, xlabel='x', ylabel='y', label='ガンマ分布', title='ガンマ分布', color='blue', save=False, addvalue=False)
plt.show()

[OUT]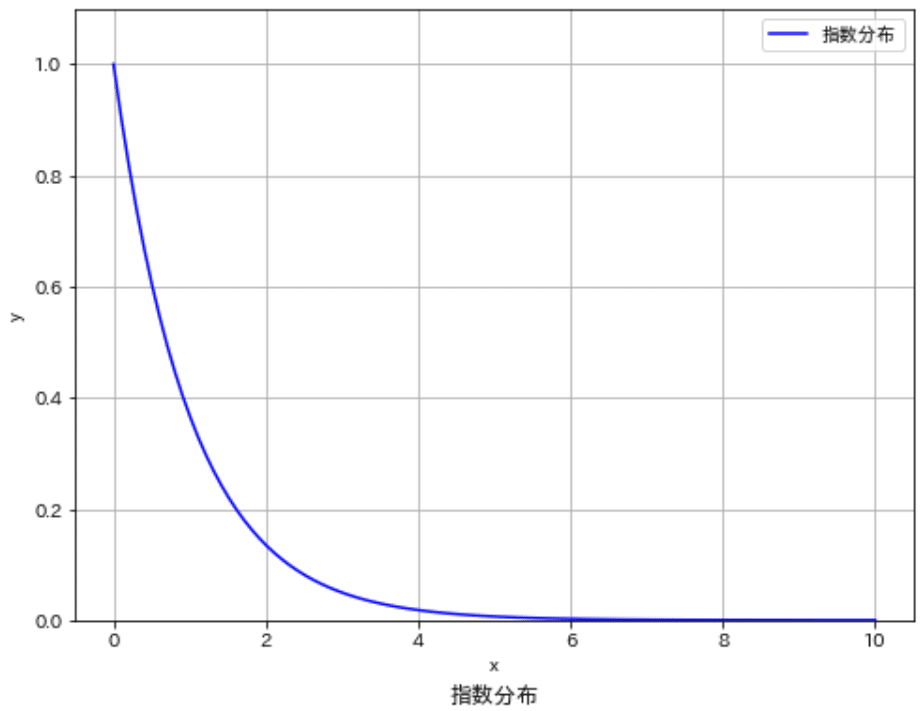

８．統計：stats - 推定／検定

　推定・検定では母集団の母数（母平均・母分散）の確率や標本間の差異を確率的に推論します。
　scipy.statsでは様々な分析が可能です。有名なものとして下記があります。

f_oneway(*samples[, axis])：1元配置分散分析（One-way ANOVA）
shapiro(x)：Shapiro-Wilk検定（正規性の検定）
MonteCarloMethod([n_resamples, batch, rvs])：モンテカルロ法

参考資料

あとがき

　作っている途中でよい資料があったの気づいた・・・・

この記事が気に入ったらサポートをしてみませんか？