Pythonで学ぶ統計学7:多変量ガウス分布
1.概要
本記事は統計学の学習記録用として作成しており、私が理解するのに時間がかかった場所や追って参照したい内容を中心にまとめております。
本記事のテーマは「多変量ガウス分布」になります。なお資料の一部に下記(CC-BY)を使用させていただきました。
2.基礎用語
過去の記事で紹介した用語を再掲載します。
2-1.平均値
平均値は複数の種類があります。 一般的に平均値とは算術平均$${\overline{x}}$$であり、全データを合計値をデータ数Nで割ったものになります。
算術平均(相加平均 / 単純平均):データ群の重心を意味する
加重平均:特定の値(特徴量)に重心が偏るようにした平均
調和平均:逆数をとって算術平均して逆数
相乗平均:全ての積を取りn 乗根で返す
$$
\begin{aligned} 平均値\overline{x} = \frac{x_1 + x_2 + \dots + x_N}{N} = \frac{1}{N} \sum^{N}_{n=1} x_{n} \end{aligned}
$$
平均値には下記特徴があります。
データの重心に近い概念のため左右の分布が同等だと中心(中央)に寄る
外れ値に弱く、過大・過小な値に(重心が)引っ張られる傾向がある(独身男性の平均資産額が急に「500万円」も増えた理由)
データ間のばらつきを最小化する理論値のため、解釈性が高い(理解しやすい)
データ数が少ないと真値からずれる可能性が高くなる
平均値の値だけで評価するのは危険であり、ばらつきなどと合わせて比較する必要がある。
2-2.分散と標準偏差σ
ばらつきはデータの散らばり度合を表す指標です。平均値を$${\bar{x} }$$、データ数nとする時、ばらつきの指標は分散と標準偏差があります。
また分散には標本分散と不偏分散があります。詳細は別記事で説明する予定ですが概要は下記の通りです。
分散$${\sigma^2}$$:平均値$${\bar{x}}$$との誤差$${(x_i - \bar{x})}$$の2乗和の平均(2乗にすることで誤差が負の値でも問題ない)
標準偏差$${\sigma}$$:分散の平方根であり、元データと同じ単位で扱うことができデータ解析のばらつきは$${\sigma}$$を使用する。データが正規分布に従う場合は±kσ間に存在するデータの確率は理論的に求まる。
標本分散と不偏分散:記述統計では使用しませんが、推測統計では不変分散が出てきます。理由として、母集団に比べ標本数が少ない時は標本分散が母分散よりも小さくため、標本分散が母分散に等しくなるように補正した分散が必要なためです。
$$
(標本)分散\sigma^2 = \frac{1}{n}\sum_{i=1}^{n} (x_i - \bar{x})^2
$$
$$
標準偏差\sigma = \sqrt{\sigma^2}
$$
$$
不偏分散\sigma^2= \frac{1}{n-1}\sum_{i=1}^{n} (x_i – \bar{x})^2
$$
Python実装時の注意点として、デフォルトでは「Numpy:標本分散、Pandas:不偏分散」の値が出力されます。Numpyで不偏分散を計算する場合は引数"ddof=1"とします。
自分が求める手法にあった統計値を選定する必要があります。
[IN]
x = np.random.randn(100)
mean, var, std = x.mean(), x.var(), x.std()
print(f'Numpy 平均:{mean:.3f}, 分散: {var:.3f}, 標準偏差: {std:.3f}')
mean, var, std = x.mean(), x.var(ddof=1), x.std(ddof=1)
print(f'Numpy 平均:{mean:.3f}, 分散: {var:.3f}, 標準偏差: {std:.3f}')
df_x = pd.DataFrame(x, columns=['x'])
mean, var, std = df_x['x'].mean(), df_x['x'].var(), df_x['x'].std()
print(f'Pandas 平均:{mean:.3f}, 分散: {var:.3f}, 標準偏差: {std:.3f}')
[OUT]
Numpy 平均:0.027, 分散: 1.273, 標準偏差: 1.128
Numpy 平均:0.027, 分散: 1.286, 標準偏差: 1.134
Pandas 平均:0.027, 分散: 1.286, 標準偏差: 1.1342-3.相関
2つのデータ間の関係を表す指標としては共分散と相関係数があります。共分散はデータのスケールで値が変わるため通常は相関係数を使用します。
共分散:2変数($${x}$$, $${y}$$)の関係の強さを表す指標の一つであり「$${X}$$の偏差 × $${Y}$$の偏差の平均」となる。注意点としてスケール変換に対して不変でなくデータの単位の影響を受けるので値の大きさで単純に比較できない。
相関係数:2 変量データの間にある相関関係(= 線形な関係)の強弱を示す指標であり‐1.0から1.0の範囲で表される。
2-3-1.共分散:Cov(X, Y)
共分散(Covariance)は下記の通りであり「X の偏差 × Y の偏差」の平均」を意味します。特徴は下記の通りです。
共分散が大きい(正)→ $${X}$$ が大きいとき Y$${Y}$$も大きい(同じ方向に動く)
共分散が 0に近い→ $${X}$$ と $${Y}$$ にあまり関係はない(独立である)
共分散が小さい(負)→ $${X}$$ が大きいとき $${Y}$$は小さい(違う方向に動く)
共分散の意味として”多次元での分散”に近く、2次元の正規分布における分散(の一部)に使用される
$${X}$$=$${Y}$$の場合は1次元の分散と同じ形になる->共分散は分散の一般化
数値($${X}$$や$${Y}$$)の大小で共分散の数値の大きさが変わるため、$${Cov()}$$の数値比較には意味がない(※1次元でも身長と体重の分散の比較は意味がないのと同じ意味)。
よって$${Cov()}$$の大小だけでどの程度の相関があるかは判断できない。
$$
共分散{{\rm Cov}(X,Y)} = \frac{1}{n}\sum_{i=1}^{n}(x_i -\bar{x})(y_i - \bar{y})
$$
$$
Xの分散\sigma^2 = \frac{1}{n}\sum_{i=1}^{n} (x_i - \bar{x})(x_i - \bar{x})
$$
$$
Yの分散\sigma^2 = \frac{1}{n}\sum_{i=1}^{n} (y_i - \bar{y})(y_i - \bar{y})
$$
2-3-2.相関係数:Corr(X, Y)
前述の通り共分散$${Cov(X,Y)}$$の絶対値では他の$${Cov()}$$との比較はできず、値から相関関係の程度を把握できないため正規化する必要があります。$${Cov(X,Y)}$$を-1~1に正規化した値が相関係数となります。相関係数$${{\rm Corr}(X, Y)}$$は数式より下記特徴があります。
【相関係数rの傾向や特徴】
相関係数は共分散Cov(X,Y)を各変数X, Yの標準偏差σで割った値である
標準化(平均0, 分散1)されているため他の相関係数とも比較が可能
各変数のスケールを変更しても標準化されるため、片方を定数倍しても相関係数の値は変わらない(データの大小に依存しない)
相関係数の性質として下記がある。
性質1:値は-1~1であり変数X,Yのスケールによらず比較できる
性質2:Corr(X,Y)の値の大小でXとYの関係性が判断できる
性質3:Corr(X,Y)=1のときXとYの値は全て同一線上となる
相関係数rは基本的に線形の関係度(強さ)を示す。よってsignカーブなど関係があっても線形関係に無いものはrが小さくなる(※無相関だとしても無関係とは限らないことを意味します。)
相関係数rの数値の大きさで線形関係が強いかを示す
傾きには依存せず、ばらつき度合いが同じであれば同じrとなる。
【数式】
$$
{\rm Corr}(X, Y)
=\frac{共分散}{\sqrt{xの分散 \times yの分散}}
=\frac{{\rm Cov}(X, Y)}{\sqrt{{\rm Var}(X){\rm Var}(Y)}}
=\frac{{\rm Cov}(X, Y)}{\sigma_x \sigma_y}
$$
$$
=\frac{\frac{1}{n}\sum_{i = 1}^n (x_i - \bar{x})(y_i - \bar{y})} {\sqrt{\frac{1}{n}\sum_{i = 1}^n (x_i - \bar{x})^2}\sqrt{\frac{1}{n}\sum_{i = 1}^n (y_i - \bar{y})^2}}= \frac{\frac{1}{n}\sum_{i = 1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sigma_x \sigma_y}
$$
$$
=\frac{1}{n}\sum_{i=1}^n \frac{x_i - \bar{x}}{\sigma_x} \cdot \frac{y_i - \bar{y}}{\sigma_y}
=\frac{1}{n}\sum_{i=1}^n(標準化x)(標準化y)
$$
相関係数はPandas:corr()、Numpy:corrcoef()で計算できます。
[IN]
df_2018_men, df_2018_women = df_2018_main[['年齢階級', '平均値_身長(cm)_男性']], df_2018_main[['年齢階級', '平均値_身長(cm)_女性']]
display(HorizontalDisplay(df_2018_men.T, df_2018_women.T))
df_2018_main.corr()
[OUT]
平均値_身長(cm)_男性 平均値_身長(cm)_女性
平均値_身長(cm)_男性 1.000000 0.988219
平均値_身長(cm)_女性 0.988219 1.0000002-4.正規分布(ガウス分布)
正規分布(ガウス分布)の概要は下記の通りです(平均:$${\mu}$$、標準偏差:$${\sigma}$$)。
特徴
平均値を中心として左右対称の釣り鐘型(Bell Curve)であり、標準偏差$${\sigma}$$間に入る確率は決まっている(例:$${\mu}$$±1.96$${\sigma}$$の範囲にデータの95%が含まれる)。
正規分布同士の差も正規分布となる。
パラメータ
正規分布:平均$${\mu}$$、標準偏差$${\sigma}$$の分布
標準正規分布:平均$${0}$$、標準偏差$${1}$$
事象例:自然現象に基づくばらつき



$$
正規分布:\displaystyle X\sim N(\mu ,\sigma ^{2})=\mathcal{N}(x|μ, \sigma^2)=\dfrac{1}{\sqrt{2\pi\sigma^2}}\exp(-\dfrac{(x-\mu)^ 2}{2\sigma^ 2})
$$
$$
標準正規分布f(x)=\mathcal{N}(x|0, 1)=\dfrac{1}{\sqrt{2\pi}}\exp(-\dfrac{x^ 2}{2})
$$
Pythonでの実装は下記の通りです。
[IN] #正規分布 :平均0、標準偏差1
mean, std = 0, 1
x = np.arange(-5, 5, 0.01)
y = stats.norm.pdf(x, loc=mean, scale=std)
showGraph_mstd(x, y, mean, std, '正規分布', verbose=True)
[OUT]
【コラム:正規分布を分解してみる】
下図の通り正規分布を式内の$${(x-\mu)^ 2}$$から変換して作成可能です。

3.多変量ガウス分布:理論編
多変量ガウス分布(多変量正規分布、多次元正規分布、結合正規分布などとも呼ぶ)は1次元の正規分布を高次元へと一般化した確率分布です。 数式は下記の通りとなります。
本記事では扱いませんが共分散行列の逆行列$${\boldsymbol{\Sigma}^{-1}}$$は精度行列(precision matrix)とも呼ばれます。
$$
p(x)=f(x;μ,Σ) = \frac{1}{\sqrt{(2\pi)^{n}|\Sigma|}}\exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)
$$
$${\boldsymbol{x}}$$:確率変数の$${n}$$次元のベクトル
$${\boldsymbol{\mu}}$$:平均値を表す$${n}$$次元のベクトル
$${\boldsymbol{\Sigma}}$$:共分散行列を表す$${n\times n}$$行列
$${\boldsymbol{\Sigma}^{-1}}$$:共分散行列の逆行列(精度行列)
$${(\boldsymbol{x}-\boldsymbol{\mu})^{\mathrm{T}}}$$:$${\boldsymbol{x}-\boldsymbol{\mu}}$$の転置

3-1.多変量ガウス分布の特徴/性質
多変量ガウス分布の特徴は下記の通りです。
分布の中心は平均値ベクトル$${\boldsymbol{\mu}}$$となる。
分布の幅と形状は共分散行列:$${\boldsymbol{\Sigma}}$$に依存する
多変量ガウス分布は$${\boldsymbol{\mu}}$$と:$${\boldsymbol{\Sigma}}$$の2つで特徴づけさせる
ある変数の部分集合についての情報が与えられたとき、他の変数の条件付き分布を求めることができ、この分布は多変量ガウス分布に従う
3-2.サンプルデータと統計量
本節から実際の数値を使用して2次元の多変量ガウス分布(二変量ガウス分布)の理解を深めていきます。
2次元のサンプルデータを$${X}$$($${x_1, x_2}$$は縦ベクトル)として、各次元の統計量を計算しておきます。今回の計算では標本分散で計算しましたが、実際の連続データであれば不偏分散の方がよいと思います。
【サンプルデータ】
$$
X
=\begin{bmatrix}\mid & \mid\\ x_1 & x_2 \\ \mid & \mid \end{bmatrix}
=\begin{bmatrix} 0.686 & -2.072 \\ 0.542 & -0.666 \\ 1.891 & -0.566 \\ 0.562 & 0.936 \\ -0.307 & -0.861 \\ -0.639 & 0.397 \end{bmatrix}
$$
【平均値$${\mu}$$】
$$
\begin{aligned} \mu_{1} &= \frac{0.686 + 0.542 + 1.891 + 0.562 - 0.307 - 0.639}{6} = 0.4558 \\ \mu_2 &= \frac{-2.072 - 0.666 - 0.566 + 0.936 - 0.861 + 0.397}{6} = -0.4720 \end{aligned}
$$
【標本分散$${\sigma^2}$$】
$$
\begin{aligned} \sigma_1^2 &= \frac{(0.686 - 0.4558)^2 + (0.542 - 0.4558)^2 + (1.891 - 0.4558)^2 + (0.562 - 0.4558)^2 + (-0.307 - 0.4558)^2 + (-0.639 - 0.4558)^2}{6 } = 0.6520 \\ \sigma_2^2 &= \frac{(-2.072 + 0.4720)^2 + (-0.666 + 0.4720)^2 + (-0.566 + 0.4720)^2 + (0.936 + 0.4720)^2 + (-0.861 + 0.4720)^2 + (0.397 + 0.4720)^2}{6 } = 0.9159 \end{aligned}
$$
【共分散$${\text{Cov}(X, Y)}$$】
$$
\begin{aligned}
\text{Cov}(X, Y) = \frac{1}{6} \sum_{i=1}^6 (X_i - \bar{X})(Y_i - \bar{Y})
\\=\frac{1}{6}((x_1 - \mu_{1})(y_1 - \mu_{2}) + (x_2 - \mu_{1})(y_2 - \mu_{2}) + \cdots + (x_6 - \mu_{1})(y_6 - \mu_{2}))
\\=-0.171
\end{aligned}
$$
[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
#サンプルデータ
data =np.array([[ 0.686, -2.072],
[ 0.542, -0.666],
[ 1.891, -0.566],
[ 0.562, 0.936],
[-0.307, -0.861],
[-0.639, 0.397]])
mean1, mean2 = np.mean(data, axis=0)
var1, var2 = np.var(data, axis=0) # 標本分散(Numpy) ※Pandasは不変分散
std1, std2 = np.std(data, axis=0)
cov = np.cov(data, rowvar=0, bias=1)
print(f'Data1 平均: {mean1:.4f}, 分散: {var1:.4f} , 標準偏差: {std1:.4f}')
print(f'Data2 平均: {mean2:.4f}, 分散: {var2:.4f} , 標準偏差: {std2:.4f}')
print('分散共分散行列')
display(cov)
fig, ax = plt.subplots(1, 1, figsize=(10, 6), facecolor='w')
ax.scatter(data[:, 0], data[:, 1], c='blue', marker='o', label='データ')
ax.scatter(mean1, mean2, c='red', marker='x', label='平均値(データの重心)')
ax.set(xlabel=r'$x_1$(データ1)', ylabel=r'$x_2$(データ2)')
ax.grid(), ax.legend()
plt.show()[OUT]
Data1 平均: 0.4558, 分散: 0.6520 , 標準偏差: 0.8075
Data2 平均: -0.4720, 分散: 0.9159 , 標準偏差: 0.9570
分散共分散行列
array([[ 0.652, -0.171],
[-0.171, 0.916]])
3-3.分散共分散行列
分散共分散行列$${\Sigma}$$とは各次元の分散と共分散をまとめた行列となります。
$$
\sum = \begin{pmatrix} \sigma_1^2 & \sigma_{12} \cdots & \sigma_{1i} & \cdots & \sigma_{1n}\\ \sigma_{21} & \sigma_2^2 \cdots & \sigma_{2i} & \cdots & \sigma_{2n}\\ \vdots & \ddots & & & \vdots \\ \sigma_{i1} & & \sigma_{i}^2 & & \sigma_{in} \\ \vdots & & & \ddots & \vdots \\ \sigma_{n1} & \cdots & \sigma_{ni} & \cdots & \sigma_{n}^2 \end{pmatrix}
$$
3-3-1.分散共分散行列の特徴
色付きで書き換えた図を示します。図より下記が確認できます。
行列の対角成分は各次元(各データ)における分散を示す。
対角を除く値は、2種の次元における共分散を示す。
共分散は次元が入れ替わっても同じ値になるため、分散共分散行列は対角を軸とした線対称の値となる(例:$${\sigma_{12}=\sigma_{21}}$$)。
(次項でも説明しますが)1つの行列(分散共分散行列)の中に「各次元の分散」と「次元ごとの共分散」の情報を持つ

3-3-2.2次元の分散共分散行列から理解
サンプルデータは2次元であり、既に分散、共分散は算出済みのため分散共分散行列は下記の通りです。式より下記のことが確認できます。
分散共分散行列の中にはx軸方向のばらつき($${x_1}$$の分散)、y軸方向のばらつき($${x_2}$$の分散)、斜め方向の関係($${x_1, x_2}$$の共分散)の情報が含まれる。
2次元の分散共分散行列では2次元平面におけるデータ全体のばらつきを表現できる。
$$
\Sigma
= \begin{bmatrix} \sigma_{1}^2 & \text{Cov}(x_1, x_2) \\ \text{Cov} (x_2, x_1)& \sigma_{2}^2 \end{bmatrix}
=\begin{bmatrix} 0.652 & -0.171 \\ -0.171& 0.916 \end{bmatrix}
$$

3-4.二変量多変量ガウス分布
再掲載しますが多変量ガウス分布の数式は下記の通りです。多次元で複雑ですが基本的には(連続値のため)確率密度関数であり計算結果は確率密度となります。つまり各次元のデータが同時に出現する確率を表現しています。
$$
p(x)=f(x;μ,Σ) = \frac{1}{\sqrt{(2\pi)^{n}|\Sigma|}}\exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)
$$
[IN]
#多変量ガウス分布の確率密度関数
def multi_normaldistribution(X, mu, sigma):
k = len(mu) # 次元
sigma_det = np.linalg.det(sigma) # 行列式:Σ
sigma_inv = np.linalg.inv(sigma) # 逆行列:Σ^-1
N = np.sqrt((2*np.pi)**k * sigma_det) # 定数項(分母)
#einsum(アインシュタインの縮約記法)による多次元配列の掛け算
#データ点と平均ベクトルの差を計算し、それを共分散行列の逆行列で重み付けした後、再びデータ点と平均ベクトルの差で総和積を取ることで、多変量ガウス分布の指数部分の計算
fac = np.einsum('...k,kl,...l->...', X-mu, sigma_inv, X-mu) #...:任意の次元, k,l:特定の次元, ->(X-μ)^TΣ^-1(X-μ)
return np.exp(-fac/2) / N
prob_density = multi_normaldistribution(data, [mean1, mean2], cov)
prob_density[OUT]
array([0.052, 0.206, 0.042, 0.064, 0.111, 0.069])ライブラリを使用する場合はSicpyの「scipy.stats.multivariate_normal」で実装できます。
[IN]
from scipy.stats import multivariate_normal
multivariate_normal.pdf(data, [mean1, mean2], cov)[OUT]
array([0.052, 0.206, 0.042, 0.064, 0.111, 0.069])3ー5.可視化
二変量ガウス分布を可視化します。プロットは3次元となるため①等高線図、②3Dプロットの2種類でプロットしました。
[IN]
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
print(f'Data1 平均: {mean1:.4f}, 分散: {var1:.4f} , 標準偏差: {std1:.4f}')
print(f'Data2 平均: {mean2:.4f}, 分散: {var2:.4f} , 標準偏差: {std2:.4f}')
corr = np.corrcoef(data, rowvar=0)
print(f'相関係数:{corr[0, 1]:.4f}')
# グリッドを作成
x = np.linspace(-2.5, 2.5, 100)
y = np.linspace(-2.5, 2.5, 100)
X, Y = np.meshgrid(x, y)
XY = np.stack([X, Y], axis=-1)
#多変量ガウス分布
prob_density = multi_normaldistribution(XY, [mean1, mean2], cov)
# 等高線プロット
fig = plt.figure(figsize=(8, 6), facecolor='w')
plt.contourf(X, Y, prob_density)
plt.scatter(data[:, 0], data[:, 1], color='red', marker='o')
plt.colorbar(label='Probability Density')
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')
plt.title('Contour plot of the probability density function')
plt.xticks(np.arange(-2.5, 2.5, 0.5)), plt.yticks(np.arange(-2.5, 2.5, 0.5))
plt.grid()
plt.show()
# 3Dプロット
fig = plt.figure(figsize=(8, 8), facecolor='w')
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, prob_density, alpha=0.7, cmap='viridis')
ax.scatter(data[:, 0], data[:, 1], np.zeros(data.shape[0]), color='red', marker='o')
ax.set_xlabel(r'$x_1$')
ax.set_ylabel(r'$x_2$')
ax.set_zlabel('Probability Density')
ax.set_title('3D plot of the probability density function')
plt.show()
[OUT]
Data1 平均: 0.4558, 分散: 0.6520 , 標準偏差: 0.8075
Data2 平均: -0.4720, 分散: 0.9159 , 標準偏差: 0.9570
相関係数:-0.2211

プロットを見ると下記のようなことが確認できます。
平均値を重心としてやや右下方向に下がった分布が確認された
x軸($${x_1}$$)の標準偏差$${\sigma_1=0.8}$$である。二変量ガウス分布の分布をみると平均値(重心)から$${±2\sigma_1}$$程度の広がりがある
y軸($${x_2}$$)の標準偏差$${\sigma_2=0.96}$$である。二変量ガウス分布の分布をみると平均値(重心)から$${±2\sigma_2}$$程度の広がりがある
相関係数を計算すると-0.22であり少し負の相関があるためx軸が正に行くとy軸は負の方向に動く。分布をみると少し右下に分布が偏っており相関係数と同じ傾向が出ている(x軸の値が大きくなるとy軸は小さい値がでる確率が大きくなる)
二変量ガウス分布を用いることで2次元のデータにおける同時分布(確率)を表現することが出来た。
4.多変量ガウス分布:作成編
1次元正規分布は平均値$${\mu}$$, 標準偏差$${\sigma}$$から計算でき、$${\mu}$$を中心とした$${\sigma}$$に応じた広がりを持つ確率密度分布が得られます。
$$
正規分布:\displaystyle X\sim N(\mu ,\sigma ^{2})=\mathcal{N}(x|μ, \sigma^2)=\dfrac{1}{\sqrt{2\pi\sigma^2}}\exp(-\dfrac{(x-\mu)^ 2}{2\sigma^ 2})
$$
[IN]
from scipy.stats import norm
#1次元ガウス分布
mean1, mean2, mean3 = -2, 0, 2 # 平均値
std1, std2, std3 = 0.5, 1, 2 # 標準偏差
X = np.linspace(-5, 5, 100)
y1 = norm.pdf(X, mean1, std1) # 平均値:-2, 標準偏差:0.5
y2 = norm.pdf(X, mean2, std2) # 平均値:0, 標準偏差:1
y3 = norm.pdf(X, mean3, std3) # 平均値:2, 標準偏差:2
fig, ax = plt.subplots(figsize=(8, 6), facecolor='w')
ax.plot(X, y1, label=r'$\mu=-2, \sigma=0.5$')
ax.plot(X, y2, label=r'$\mu=0, \sigma=1$')
ax.plot(X, y3, label=r'$\mu=2, \sigma=2$')
ax.set(xlabel=r'$x$', ylabel=r'$p(x)$', title='1D Gaussian Distribution')
ax.grid(), ax.legend()
plt.show()
[OUT]
多変量ガウス分布も同様に平均値ベクトル$${\bf \mu}$$、分散共分散行列$${\Sigma}$$(つまり各次元の分散と次元ごとの共分散)があれば分布を作成できます。
$$
p(x)=f(x;μ,Σ) = \frac{1}{\sqrt{(2\pi)^{n}|\Sigma|}}\exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)
$$
本章では各数値において分布がどのようになるか確認していきます。事前に多変量ガウス分布計算用ライブラリと可視化関数は準備しておきます。
[IN]
from scipy.stats import multivariate_normal
# 等高線プロット
def plot_simplecontour(X, Y, prob_density):
fig = plt.figure(figsize=(8, 6), facecolor='w')
plt.contourf(X, Y, prob_density)
plt.colorbar(label='Probability Density')
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')
plt.title('Contour plot of the probability density function')
plt.xticks(np.arange(-2.5, 2.5, 0.5)), plt.yticks(np.arange(-2.5, 2.5, 0.5))
plt.grid()
plt.show()
x = np.linspace(-2.5, 2.5, 100)
y = np.linspace(-2.5, 2.5, 100)
X, Y = np.meshgrid(x, y)
XY = np.stack([X, Y], axis=-1)
print(f'形状 x: {x.shape}, y: {y.shape}, X: {X.shape}, Y: {Y.shape}, XY: {XY.shape}')[OUT]
データ形状確認 x: (100,), y: (100,), X: (100, 100), Y: (100, 100), XY: (100, 100, 2)4-1.Case1:平均0, 分散1, 共分散0
条件は下記の通りです。数値的に下記のようなグラフが想定されます。
分布の中心は(x, y)=(0,0)
x軸方向の広がりは$${\sigma_{1}=1}$$のため$${±2\sigma_{1}}$$程度
y軸方向の広がりは$${\sigma_{2}=1}$$のため$${±2\sigma_{1}}$$程度
共分散$${Cov(x,y)=0}$$、つまり各次元は独立であり関係がない:x, yに相関が無いため丸い分布となる
$$
\begin{aligned}
\bf\mu=\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix} =\begin{bmatrix} 0 \\ 0 \end{bmatrix}
, \Sigma=\begin{bmatrix} \sigma_{1}^2 & \sigma_{12}\\ \sigma_{21}& \sigma_{2}^2 \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}
\end{aligned}
$$
[IN]
means = np.array([0, 0]) # 平均ベクトル
#標準偏差(x, y)=(1, 1), 共分散Cov(x, y)=0
V_Cov_matrix = np.array([[1, 0],
[0, 1]]) # 行列
prob_density = multivariate_normal.pdf(XY, means, V_Cov_matrix)
plot_simplecontour(X, Y, prob_density)
[OUT]
4-2.Case2:平均0, 分散0.2, 共分散0
条件は下記の通りです。数値的に下記のようなグラフが想定されます。
分布の中心は(x, y)=(0,0)
$${\sigma_{1}, \sigma_{2}}$$は先ほどより小さいためx, y軸の分布の広がりが小さくなる
共分散$${Cov(x,y)=0}$$、つまり各次元は独立であり関係がない:x, yに相関が無いため丸い分布となる
結論としてCase1のグラフと形状は同じだが分布が小さいグラフができる
$$
\begin{aligned}
\bf\mu=\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix} =\begin{bmatrix} 0 \\ 0 \end{bmatrix}
, \Sigma=\begin{bmatrix} \sigma_{1}^2 & \sigma_{12}\\ \sigma_{21}& \sigma_{2}^2 \end{bmatrix}=\begin{bmatrix} 0.2 & 0 \\ 0 & 0.2 \end{bmatrix}
\end{aligned}
$$
[IN]
means = np.array([0, 0]) # 平均ベクトル
V_Cov_matrix = np.array([[0.2, 0],
[0, 0.2]]) # 行列
prob_density = multivariate_normal.pdf(XY, means, V_Cov_matrix)
plot_simplecontour(X, Y, prob_density)
[OUT]
4-3.Case3:平均0, 分散1.0, 共分散0.9
条件は下記の通りです。数値的に下記のようなグラフが想定されます。
分布の中心は(x, y)=(0,0)
$${\sigma_{1}, \sigma_{2}}$$はCase1と同じため広がりは同等
共分散$${Cov(x,y)=0.9}$$であり正の相関がある。相関係数は$${\frac{{\rm Cov}(X, Y)}{\sigma_x \sigma_y}}$$のため、かなり強い相関がありそう。
上記より、x軸・y軸の広がりはCase1と同じ、かつ右上がり(正の相関)の分布となる。結果として分布そのものの幅は小さくなる
$$
\begin{aligned}
\bf\mu=\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix} =\begin{bmatrix} 0 \\ 0 \end{bmatrix}
, \Sigma=\begin{bmatrix} \sigma_{1}^2 & \sigma_{12}\\ \sigma_{21}& \sigma_{2}^2 \end{bmatrix}=\begin{bmatrix} 1.0 & 0.9 \\0.9 &1.0 \end{bmatrix}
\end{aligned}
$$
[IN]
means = np.array([0, 0]) # 平均ベクトル
V_Cov_matrix = np.array([[1.0, 0.9],
[0.9, 1.0]]) # 行列
prob_density = multivariate_normal.pdf(XY, means, V_Cov_matrix)
plot_simplecontour(X, Y, prob_density)
[OUT]
4-4.Case4:平均0, 分散1.0, 共分散-0.9
条件は下記の通りです。Case3から共分散$${Cov(x,y)}$$を逆符号にしているだけのためx=0を軸とした線対称の分布が作成されます。
$$
\begin{aligned}
\bf\mu=\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix} =\begin{bmatrix} 0 \\ 0 \end{bmatrix}
, \Sigma=\begin{bmatrix} \sigma_{1}^2 & \sigma_{12}\\ \sigma_{21}& \sigma_{2}^2 \end{bmatrix}=\begin{bmatrix} 1.0 & -0.9 \\-0.9 &1.0 \end{bmatrix}
\end{aligned}
$$
[IN]
means = np.array([0, 0]) # 平均ベクトル
V_Cov_matrix = np.array([[1.0, -0.9],
[-0.9, 1.0]]) # 行列
prob_density = multivariate_normal.pdf(XY, means, V_Cov_matrix)
plot_simplecontour(X, Y, prob_density)
[OUT]
4-5.Case5:平均0, 分散1.0, 共分散0.999
条件は下記の通りです。Case3の共分散$${Cov(x,y)}$$を最大化したため、Case3に対してx軸・y軸の広がりは同じですが、よりシャープ(正の相関が強くなるため軸を固定した時の分布$${P(y|x)}$$が小さくなる)になります。
(参考までにこの条件で$${Cov(x,y)=1.0}$$とすると逆行列が存在しなくなりエラーとなるため、$${Cov(x,y)=0.999}$$としました。)
$$
\begin{aligned}
\bf\mu=\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix} =\begin{bmatrix} 0 \\ 0 \end{bmatrix}
, \Sigma=\begin{bmatrix} \sigma_{1}^2 & \sigma_{12}\\ \sigma_{21}& \sigma_{2}^2 \end{bmatrix}=\begin{bmatrix} 1.0 & 0.999 \\0.999 &1.0 \end{bmatrix}
\end{aligned}
$$
[IN]
means = np.array([0, 0]) # 平均ベクトル
V_Cov_matrix = np.array([[1.0, 0.999],
[0.999, 1.0]]) # 行列
prob_density = multivariate_normal.pdf(XY, means, V_Cov_matrix)
plot_simplecontour(X, Y, prob_density)
[OUT]
4-6.Case6:平均0, 分散3.0, 共分散0.999
条件は下記の通りです。数値的に下記のようなグラフが想定されます。
分布の中心は(x, y)=(0,0)
$${\sigma_{1}=3.0, \sigma_{2}=3.0}$$のためx軸、y軸の幅が広がる。
共分散$${Cov(x,y)=0.999}$$であり正の相関がある。相関係数は$${\frac{{\rm Cov}(X, Y)}{\sigma_x \sigma_y}}$$のため、分散が大きくなった分だけCase5よりは小さくなる。
結論として、x軸・y軸方向への分布は大きくなり、かつ正の相関があるため右上がりの分布となる。ただし、分散・共分散の比(つまり相関係数)を考慮するとCase4・5ほどシャープな分布にはならない。
$$
\begin{aligned}
\bf\mu=\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix} =\begin{bmatrix} 0 \\ 0 \end{bmatrix}
, \Sigma=\begin{bmatrix} \sigma_{1}^2 & \sigma_{12}\\ \sigma_{21}& \sigma_{2}^2 \end{bmatrix}=\begin{bmatrix} 3.0 & 0.999 \\0.999 &3.0 \end{bmatrix}
\end{aligned}
$$
[IN]
means = np.array([0, 0]) # 平均ベクトル
V_Cov_matrix = np.array([[3.0, 0.999],
[0.999, 3.0]]) # 行列
prob_density = multivariate_normal.pdf(XY, means, V_Cov_matrix)
plot_simplecontour(X, Y, prob_density)
[OUT]
4-7.Case7:平均1.0, 分散1.0, 共分散0
条件は下記の通りです。Case1から平均値ベクトル$${\bf \mu}$$を変更しだけですので、Case1の分布の重心がベクトルで指定した値に移動するだけとなります。
$$
\begin{aligned}
\bf\mu=\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix} =\begin{bmatrix} 1.0 \\-1.0 \end{bmatrix}
, \Sigma=\begin{bmatrix} \sigma_{1}^2 & \sigma_{12}\\ \sigma_{21}& \sigma_{2}^2 \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}
\end{aligned}
$$
[IN]
means = np.array([1.0, -1.0]) # 平均ベクトル
V_Cov_matrix = np.array([[1.0, 0],
[0, 1.0]]) # 行列
prob_density = multivariate_normal.pdf(XY, means, V_Cov_matrix)
plot_simplecontour(X, Y, prob_density)
[OUT]
5.多変量ガウス分布の応用例
多変量ガウス分布の応用例を紹介します。
5-1.クラスタリング:混合ガウスモデル
混合ガウスモデル (Gaussian Mixture Model, GMM)は多変量ガウス分布を用いてデータをクラスタリングする手法です(クラスタリングは下記記事参照)。
https://datachemeng.com/wp-content/uploads/gaussianmixturemodel.pdf
5-2.線形回帰/ベイズ線形回帰
線形回帰の誤差項$${\epsilon}$$を多変量ガウス分布と仮定して計算するモデルです。応用例としてはベイズ線形回帰があります。

5-3.状態空間モデル(カルマンフィルタ)
カルマンフィルタの技術はノイズが混じった観測データからシステムの状態を最適に推定するために使用されたりします。
5-4.確率的生成モデル(VAE)
一つの例として機械学習モデルのVariational Autoencoder(VAE)の中で多変量ガウス分布の概念が使用されております。
6.株価でのデータ分析
株式投資では分散投資の中で「卵を一つのかごに盛るな」という用語があり、ポートフォリオ(金融商品の組み合わせ)の管理が重要となります。参考として個人投資家のテスタ氏が公開したポートフォリオを紹介します。

ポートフォリオを作るうえで重要なことは「リスクとリターンのバランスを最適化すること」です。企業は各セクターで分かれておりますが、それぞれは独立ではなく従属的な関係であり、相関関係があります。例として自動車業界や建築業が好調であれば鉄鋼業界も好調になります。
分散投資では「リスクヘッジのため複数株を持つ」ことに主眼が置かれますが、もし負の相関を持つ(市場の共食い)ような株同士を持つ場合、他方が上がっても他方が下がるためリスクは小さいですがそもそもリターンも少なくなります。
多変量ガウス分布を用いて複数セクターの関係を定量的に判断することで意味のない分散投資を避け、ポートフォリオが適切かを検討ができます。実際には他の要因(市場の動向や個別企業の業績など)も検討が必要です。
本章では実データを使用して多変量ガウス分布を応用します。具体的には「J-Quants API」で各業種の株価情報を取得して、前日比からセクターごとの関係を分析しました。今回は当日での比較となりますので、時間軸がずれて相関があるかどうかの分析までは実施しておりません。
重要なこととして多変量ガウス分布で可視化できるのは「相関関係」であり「因果関係」ではありません。数値的な傾向は可視化できますが、裏にある原因と結果のつながりは解析者自身が分析する必要があります(これらの考え方については有料ですが下記記事参照)。
6-1.上場銘柄一覧を取得:J-Quants API
JPX総研(日本取引所グループ)より公開された「J-Quants API」は個人投資家向けの情報をAPIで提供してくれます。
事前準備として下記記事を元に、リフレッシュトークンー>IDトークンを取得しました。合わせて作業に必要なライブラリ、便利クラス、英文名を日本語に変えるための辞書を準備しました。
変数dataのE-mailとパスワードは各人のアカウント作成時のものに変更が必要です。

[IN]
import os
import sys
import glob
import json
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn
import japanize_matplotlib
import requests
from datetime import datetime, timedelta
from typing import List, Dict, Tuple, Union, Optional
from tqdm import tqdm
#DataFrameの表示を綺麗にする
class HorizontalDisplay:
def __init__(self, *args):
self.args = args
def _repr_html_(self):
template = '<div style="float: left; padding: 10px;">{0}</div>'
return '\n'.join(template.format(a._repr_html_()) for a in self.args)
#カラム変更用
var2description = {
'Date':'情報適用年月日',
'Code':'銘柄コード',
'CompanyName':'会社名',
'CompanyNameEnglish':'会社名(英語)',
'Sector17Code':'17業種コード',
'Sector17CodeName':'17業種コード名 ',
'Sector33Code':'33業種コード',
'Sector33CodeName':'33業種コード名',
'ScaleCategory':'規模コード',
'MarketCode':'市場区分コード',
'MarketCodeName':'市場区分名'}
data={"mailaddress":"<YOUR EMAIL_ADDRESS>", "password":"<YOUR PASSWORD>"}
res = requests.post("https://api.jquants.com/v1/token/auth_user", data=json.dumps(data))
REFRESH_TOKEN = res.json()["refreshToken"] #リフレッシュトークンを取得
#IDトークンを取得
res = requests.post(f"https://api.jquants.com/v1/token/auth_refresh?refreshtoken={REFRESH_TOKEN}")
idToken = res.json()['idToken']
print(idToken)[OUT]
<取得したIDトークンが表示される> エンドポイントの「https://api.jquants.com/v1/listed/info」にIDトークンを渡すことで上場銘柄一覧の情報を取得できます。HTTPクライアントとしてはRequentsライブラリを使用しました。
参考として全データ、およびトヨタ自動車のデータ抽出した結果を表示しました。
[IN]
headers = {'Authorization': 'Bearer {}'.format(idToken)}
res_code = requests.get("https://api.jquants.com/v1/listed/info", headers=headers)
df = pd.DataFrame(res_code.json()["info"])
df.columns = [var2description[var] for var in df.columns]
display(df)
code_toyota = df[df['会社名']=='トヨタ自動車']['銘柄コード'].values[0]
print(f'トヨタ自動車の銘柄コード:{code_toyota}')[OUT]
トヨタ自動車の銘柄コード:72030
6-2.株価四本値の取得(1データのみ):J-Quants API
エンドポイントの「https://api.jquants.com/v1/prices/daily_quotes」にクエリパラメータとして銘柄コードと日付を渡すことで指定した会社・日付の株価データが得られます。
[IN]
headers = {'Authorization': 'Bearer {}'.format(idToken)}
res = requests.get(f"https://api.jquants.com/v1/prices/daily_quotes?code={code_toyota}&date=20230206", headers=headers)
res.json()[OUT]
{'daily_quotes': [{'Date': '2023-02-06',
'Code': '72030',
'Open': 1909.0,
'High': 1934.5,
'Low': 1908.0,
'Close': 1913.5,
'Volume': 30031400.0,
'TurnoverValue': 57641247250.0,
'AdjustmentFactor': 1.0,
'AdjustmentOpen': 1909.0,
'AdjustmentHigh': 1934.5,
'AdjustmentLow': 1908.0,
'AdjustmentClose': 1913.5,
'AdjustmentVolume': 30031400.0}]}よって、確認したい「銘柄コード」と「期間」の情報があれば、過去の株価一覧を取得できます。フリープランでは2年12週間~12週間前までのデータしか取得できないため、今回は2年間分のデータでデータ分析をします。

6-3.セクターの選定
目的としては各セクターでの関係を可視化・分析することです。今回は下記セクターにおける大企業をベンチマークとして比較しました。
食品:ニッスイ
エネルギー資源:ENEOSホールディング
医薬品:武田薬品工業
自動車・輸送機:トヨタ自動車
鉄鋼・非鉄:日本製鉄
J-Quants-API記載の「17業種コード及び業種名」、「33業種コード及び業種名」からPandasを使用してデータ抽出しました。
[IN]
print(f'会社数:{len(df["会社名"].unique()):,}社')
#17業種コードで分類
df_food = df[df['17業種コード'] == '1'] # 1:食品
df_Energy = df[df['17業種コード'] == '2'] # 2:エネルギー資源
df_drug = df[df['17業種コード'] == '5'] # 5:医薬品
df_automobile = df[df['17業種コード'] == '6'] # 6:自動車・輸送機
df_iron = df[df['17業種コード'] == '7'] # 7:鉄鋼・非鉄
#プライム市場(0111)のデータだけ抽出
df_food, df_Energy, df_automobile, df_drug, df_iron = df_food[df_food['市場区分コード'] == '0111'], df_Energy[df_Energy['市場区分コード'] == '0111'], df_automobile[df_automobile['市場区分コード'] == '0111'], df_drug[df_drug['市場区分コード'] == '0111'], df_iron[df_iron['市場区分コード'] == '0111']
print(f'データ形状 食料品:{df_food.shape}, エネルギー資源:{df_Energy.shape}, 医薬品:{df_drug.shape}, 自動車・輸送機:{df_automobile.shape}, 鉄鋼・非鉄:{df_iron.shape}')
#33業種コードで絞り込み
df_food = df_food[df_food['33業種コード'] == '0050'] # 0050:水産・農林業
df_Energy = df_Energy[df_Energy['33業種コード'] == '3300'] # 3300:石油・石炭製品
df_automobile = df_automobile[df_automobile['33業種コード'] == '3700'] # 3700:輸送用機器
df_iron = df_iron[df_iron['33業種コード'] == '3450'] # 3450:鉄鋼, 3500:非鉄金属
print(f'データ形状 食料品:{df_food.shape}, エネルギー資源:{df_Energy.shape}, 医薬品:{df_drug.shape}, 自動車・輸送機:{df_automobile.shape}, 鉄鋼・非鉄:{df_iron.shape}')
#指定の会社抽出
df_toyota = df_automobile[df_automobile['会社名'] == 'トヨタ自動車']
df_Nissui = df_food[df_food['会社名'] == 'ニッスイ']
df_Eneos = df_Energy[df_Energy['会社名'] == 'ENEOSホールディングス']
df_Takeda = df_drug[df_drug['会社名'] == '武田薬品工業']
df_NipponSteel = df_iron[df_iron['会社名'] == '日本製鉄']
display(HorizontalDisplay(df_toyota, df_Nissui, df_Eneos, df_Takeda, df_NipponSteel))[OUT]
会社数:4,245社
データ形状 食料品:(78, 11), エネルギー資源:(12, 11), 医薬品:(34, 11), 自動車・輸送機:(61, 11), 鉄鋼・非鉄:(44, 11)
データ形状 食料品:(6, 11), エネルギー資源:(7, 11), 医薬品:(34, 11), 自動車・輸送機:(50, 11), 鉄鋼・非鉄:(23, 11)
6-4.株価四本値の取得(指定期間):J-Quants API
前述の通り①株価情報を取得するための情報は「銘柄コード」と「日付」、②J-Quantsのフリープランの期間は2年14週間~14週間前です。
まずは株価情報を取得するための日付を連番で作成する関数を作成します。初期値はフリープランに合わせて「2年14週間~14週間前」までの期間を取得できるようにしました。
[IN]
def generate_date_sequence(start_date: str = None, end_date: str = None) -> list:
#フリープラン:当日の12週間前までのデータを取得可能
if end_date is None:
end_date = (datetime.now() - timedelta(weeks=12)).strftime("%Y%m%d")
#フリープラン:取得可能日(12週間前)の2年前までのデータを取得可能
if start_date is None:
end_date_dt = datetime.strptime(end_date, "%Y%m%d")
start_date = end_date_dt.replace(year=end_date_dt.year - 2).strftime("%Y%m%d")
start = datetime.strptime(start_date, "%Y%m%d")
end = datetime.strptime(end_date, "%Y%m%d")
date_list = []
current_date = start
while current_date <= end:
date_list.append(current_date.strftime("%Y%m%d"))
current_date += timedelta(days=1)
return date_list
period_data = generate_date_sequence()
period_data[OUT]
['20210208',
'20210209',
'20210210',
...
'20230204',
'20230205',
'20230206',
'20230207',
'20230208']次に作成した期間データを使用して、J-Quants-APIからほしい企業の株価情報を抽出する関数を作成します。設計思想は下記の通りです。
前節で抽出したDataFrameと期間データを渡すだけで全部計算
最終的には前日比のみ使用するため一部の不要なカラムは除外できるようにclean引数を追加
期間データは連番であり土日などデータがない期間は空リストが出力される可能性がある。空リスクを含まないようにif文設定
tqdmで進捗度(プログレスバー)を表示
[IN]
def get_stockprice(df, period:List, clean:bool = True):
companyname = df['会社名'].values[0]
code = df['銘柄コード'].values[0]
headers = {'Authorization': 'Bearer {}'.format(idToken)}
outputs = []
print(f'{companyname}({code})の株価データを取得中...')
for date in tqdm(period):
res = requests.get(f"https://api.jquants.com/v1/prices/daily_quotes?code={code}&date={date}", headers=headers)
data_list = res.json()['daily_quotes']
#土日・休日のデータが無い場合は[]で出力->スキップ
if data_list:
outputs.append(data_list[0])
else:
continue
df_output = pd.DataFrame(outputs)
#欲しいデータだけ抽出
if clean:
df_output = df_output[['Date', 'Code', 'Open', 'High', 'Low', 'Close', 'Volume']]
return df_output
get_stockprice(df_toyota, period_data, clean=True)[OUT]
トヨタ自動車(72030)の株価データを取得中...
100%|██████████| 731/731 [02:32<00:00, 4.78it/s]
データ抽出は時間がかかりますので抽出したデータはPickleファイルに保存します。Pickleファイルにデータとして保存しておけば、再度データを使用したい時に高速で読み込むことができます。
Pickleファイルの作成・読み込みは全てPandasで実行可能です。なおPickleファイル作成は前述の"generate_date_sequence"で作成した期間データから自動で作成できますが値は日付によって変わるため、読み込み時のpath名は手動で修正が必要です。
[IN]
#株価データ取得
df_toyota_stock = get_stockprice(df_toyota, period_data, clean=True)
df_Nissui_stock = get_stockprice(df_Nissui, period_data, clean=True)
df_Eneos_stock = get_stockprice(df_Eneos, period_data, clean=True)
df_Takeda_stock = get_stockprice(df_Takeda, period_data, clean=True)
df_NipponSteel_stock = get_stockprice(df_NipponSteel, period_data, clean=True)
#取得したデータをPickel形式で保存
if not os.path.exists('./data'): os.makedirs('./data') #dataフォルダが無ければ作成
df_toyota_stock.to_pickle(f'data/df_toyota_stock_{period_data[0]}_{period_data[-1]}.pkl')
df_Nissui_stock.to_pickle(f'data/df_Nissui_stock_{period_data[0]}_{period_data[-1]}.pkl')
df_Eneos_stock.to_pickle(f'data/df_Eneos_stock_{period_data[0]}_{period_data[-1]}.pkl')
df_Takeda_stock.to_pickle(f'data/df_Takeda_stock_{period_data[0]}_{period_data[-1]}.pkl')
df_NipponSteel_stock.to_pickle(f'data/df_NipponSteel_stock_{period_data[0]}_{period_data[-1]}.pkl')
#保存したデータを読み込み
df_toyota_stock = pd.read_pickle('data/df_toyota_stock_20210207_20230207.pkl')
df_Nissui_stock = pd.read_pickle('data/df_Nissui_stock_20210207_20230207.pkl')
df_Eneos_stock = pd.read_pickle('data/df_Eneos_stock_20210207_20230207.pkl')
df_Takeda = pd.read_pickle('data/df_Takeda_stock_20210207_20230207.pkl')
df_NipponSteel_stock = pd.read_pickle('data/df_NipponSteel_stock_20210207_20230207.pkl')[OUT]
6-5.前日比の計算
株価の前日比を計算するための関数を作成します。前日比の計算式は下記の通りです。合わせてデータを日付と前日比のみの形状に変換しました。
$$
前日比[%]=100\times (\frac{終値-始値}{始値})
$$
[IN]
def add_DoD_ratio(df):
price_open = df['Open'] #始値
price_close = df['Close'] #終値
ratio_dayoverday = (price_close - price_open) / price_open * 100
df_output = df.copy()
df_output['前日比[%]'] = ratio_dayoverday
return df_output
#前日比を追加+データの再抽出
df_toyota_DoDratio = add_DoD_ratio(df_toyota_stock)[['Date','前日比[%]']]
df_Nissui_DoDratio = add_DoD_ratio(df_Nissui_stock)[['Date','前日比[%]']]
df_Eneos_DoDratio = add_DoD_ratio(df_Eneos_stock)[['Date','前日比[%]']]
df_Takeda_DoDratio = add_DoD_ratio(df_Takeda)[['Date','前日比[%]']]
df_NipponSteel_DoDratio = add_DoD_ratio(df_NipponSteel_stock)[['Date','前日比[%]']]
display(HorizontalDisplay(df_toyota_DoDratio, df_Nissui_DoDratio, df_Eneos_DoDratio, df_Takeda_DoDratio, df_NipponSteel_DoDratio))
[OUT]
6-6.統計量計算/前日比の時系列変化の可視化
各種統計量および前日比の時系列変化を示します。統計量やグラフからある程度情報は確認できますが、セクターごとの関係まで理解するのは難しいことが確認できます。
[IN]
import matplotlib.dates as mdates
# 平均値・分散(標本分散)・標準偏差を計算
mean_toyota, mean_Nissui, mean_Eneos, mean_Takeda, mean_NipponSteel = df_toyota['前日比[%]'].mean(), df_Nissui['前日比[%]'].mean(), df_Eneos['前日比[%]'].mean(), df_Takeda['前日比[%]'].mean(), df_NipponSteel['前日比[%]'].mean()
var_toyota, var_Nissui, var_Eneos, var_Takeda, var_NipponSteel = df_toyota['前日比[%]'].var(ddof=0), df_Nissui['前日比[%]'].var(ddof=0), df_Eneos['前日比[%]'].var(ddof=0), df_Takeda['前日比[%]'].var(ddof=0), df_NipponSteel['前日比[%]'].var(ddof=0)
std_toyota, std_Nissui, std_Eneos, std_Takeda, std_NipponSteel = df_toyota['前日比[%]'].std(ddof=0), df_Nissui['前日比[%]'].std(ddof=0), df_Eneos['前日比[%]'].std(ddof=0), df_Takeda['前日比[%]'].std(ddof=0), df_NipponSteel['前日比[%]'].std(ddof=0)
print(f'トヨタ自動車 平均値:{mean_toyota:.2f} 分散:{var_toyota:.2f} 標準偏差:{std_toyota:.2f}')
print(f'ニッスイ 平均値:{mean_Nissui:.2f} 分散:{var_Nissui:.2f} 標準偏差:{std_Nissui:.2f}')
print(f'ENEOS 平均値:{mean_Eneos:.2f} 分散:{var_Eneos:.2f} 標準偏差:{std_Eneos:.2f}')
print(f'武田薬品工業 平均値:{mean_Takeda:.2f} 分散:{var_Takeda:.2f} 標準偏差:{std_Takeda:.2f}')
print(f'日本製鐵 平均値:{mean_NipponSteel:.2f} 分散:{var_NipponSteel:.2f} 標準偏差:{std_NipponSteel:.2f}')
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.scatter(df_toyota['Date'], df_toyota['前日比[%]'], label='トヨタ自動車')
ax.scatter(df_Nissui['Date'], df_Nissui['前日比[%]'], label='ニッスイ', marker='x')
ax.scatter(df_Eneos['Date'], df_Eneos['前日比[%]'], label='ENEOS', marker='^')
ax.scatter(df_Takeda['Date'], df_Takeda['前日比[%]'], label='武田薬品工業', marker='*')
ax.scatter(df_NipponSteel['Date'], df_NipponSteel['前日比[%]'], label='日本製鐵', marker='s', color='grey', alpha=0.5)
ax.plot(df_toyota['Date'], np.zeros_like(df_toyota['前日比[%]']), color='black', linestyle='-') #基準線
#軸目盛の設定
ax.xaxis.set_major_locator(mdates.DayLocator(bymonthday=None, interval=30, tz=None))
ax.set(xlabel='Date', ylabel='前日比[%]', title='前日比の時系列変化')
ax.grid(), ax.legend()
plt.setp(ax.get_xticklabels(), rotation=90, ha="right", rotation_mode="anchor")
plt.show()[OUT]
トヨタ自動車 平均値:-0.02 分散:1.49 標準偏差:1.22
ニッスイ 平均値:-0.00 分散:1.81 標準偏差:1.35
ENEOS 平均値:-0.04 分散:1.14 標準偏差:1.07
武田薬品工業 平均値:0.01 分散:0.68 標準偏差:0.82
日本製鐵 平均値:0.06 分散:2.50 標準偏差:1.58
トヨタ自動車と日本製鉄のみデータを抽出した結果も示します。
[IN]
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.scatter(df_toyota['Date'], df_toyota['前日比[%]'], label='トヨタ自動車')
ax.scatter(df_NipponSteel['Date'], df_NipponSteel['前日比[%]'], label='日本製鐵', marker='s', color='grey', alpha=0.5)
ax.plot(df_toyota['Date'], np.zeros_like(df_toyota['前日比[%]']), color='black', linestyle='-') #基準線
#軸目盛の設定
ax.xaxis.set_major_locator(mdates.DayLocator(bymonthday=None, interval=30, tz=None))
ax.set(xlabel='Date', ylabel='前日比[%]', title='前日比の時系列変化')
ax.grid(), ax.legend()
plt.setp(ax.get_xticklabels(), rotation=90, ha="right", rotation_mode="anchor")
plt.show()
[OUT]
6-7.分散共分散行列と相関係数の算出
株購入時は「この株は絶対上がる」という企業+「ポートフォリオ最適化のための分散投資用企業」を選定するとします。今回は「トヨタ自動車(自動車)」をベンチマークとして、他のセクターとの関係を確認しました。
トヨタ自動車の前日比と各社の分散共分散行列および相関係数を確認しました。行列・係数の計算はNumpyを使用しており標本分散で計算しました。
結果より下記が確認できます。
選定セクターの中では、自動車と鉄鋼の相関が最も大きい
選定セクターの中では、自動車と食品の相関が最も小さい
日本製鉄の前日比の分散=2.5であり比較的ばらつきが大きい。相関関係が他より高いため、共分散の値も大きくなっている。
[IN]
cov_To_Ni = np.cov(df_toyota['前日比[%]'], df_Nissui['前日比[%]'], ddof=0) #ddof=0で標本分散
cov_To_Ene = np.cov(df_toyota['前日比[%]'], df_Eneos['前日比[%]'], ddof=0)
cov_To_Ta = np.cov(df_toyota['前日比[%]'], df_Takeda['前日比[%]'], ddof=0)
cov_To_NS = np.cov(df_toyota['前日比[%]'], df_NipponSteel['前日比[%]'], ddof=0)
print(f'トヨタ自動車とニッスイの分散共分散行列:\n{cov_To_Ni}', end='\n\n')
print(f'トヨタ自動車とENEOSの分散共分散行列:\n{cov_To_Ene}', end='\n\n')
print(f'トヨタ自動車と武田薬品工業の分散共分散行列:\n{cov_To_Ta}', end='\n\n')
print(f'トヨタ自動車と日本製鐵の分散共分散行列:\n{cov_To_NS}', end='\n\n')
corr_To_Ni = np.corrcoef(df_toyota['前日比[%]'], df_Nissui['前日比[%]'])
corr_To_Ene = np.corrcoef(df_toyota['前日比[%]'], df_Eneos['前日比[%]'])
corr_To_Ta = np.corrcoef(df_toyota['前日比[%]'], df_Takeda['前日比[%]'])
corr_To_NS = np.corrcoef(df_toyota['前日比[%]'], df_NipponSteel['前日比[%]'])
print(f'トヨタ自動車との相関係数 ニッスイ:{corr_To_Ni[0,1]:.2f}, ENEOS:{corr_To_Ene[0,1]:.2f}, 武田薬品工業:{corr_To_Ta[0,1]:.2f}, 日本製鐵:{corr_To_NS[0,1]:.2f}')[OUT]
トヨタ自動車とニッスイの分散共分散行列:
[[1.48746281 0.33183264]
[0.33183264 1.81080768]]
トヨタ自動車とENEOSの分散共分散行列:
[[1.48746281 0.3405704 ]
[0.3405704 1.13631713]]
トヨタ自動車と武田薬品工業の分散共分散行列:
[[1.48746281 0.29143276]
[0.29143276 0.67954114]]
トヨタ自動車と日本製鐵の分散共分散行列:
[[1.48746281 0.63165275]
[0.63165275 2.50369072]]
トヨタ自動車との相関係数 ニッスイ:0.20, ENEOS:0.26, 武田薬品工業:0.29, 日本製鐵:0.336-8.データの前処理:2次元配列化
平均値と分散共分散行列は計算したため多変量ガウス分布を作成できます。
$$
p(x)=f(x;μ,Σ) = \frac{1}{\sqrt{(2\pi)^{n}|\Sigma|}}\exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)
$$
可視化のために3Dプロットも作成しますので、計算用として2次元配列の作成をしておきます。
[IN]
#多変量ガウス分布の確率密度関数
def multi_normaldistribution(X, mu, sigma):
k = len(mu) # 次元
sigma_det = np.linalg.det(sigma) # 行列式:Σ
sigma_inv = np.linalg.inv(sigma) # 逆行列:Σ^-1
N = np.sqrt((2*np.pi)**k * sigma_det) # 定数項(分母)
#einsum(アインシュタインの縮約記法)による多次元配列の掛け算
#データ点と平均ベクトルの差を計算し、それを共分散行列の逆行列で重み付けした後、再びデータ点と平均ベクトルの差で総和積を取ることで、多変量ガウス分布の指数部分の計算
fac = np.einsum('...k,kl,...l->...', X-mu, sigma_inv, X-mu) #...:任意の次元, k,l:特定の次元, ->(X-μ)^TΣ^-1(X-μ)
return np.exp(-fac/2) / N
def convert_2dim4dist(df1, df2, column:str='前日比[%]'):
data1 = df1[column].values
data2 = df2[column].values
output = np.array([data1, data2]).T #2次元配列に変換
return output
data_To_Ni = convert_2dim4dist(df_toyota, df_Nissui, column='前日比[%]')
data_To_Ene = convert_2dim4dist(df_toyota, df_Eneos, column='前日比[%]')
data_To_Ta = convert_2dim4dist(df_toyota, df_Takeda, column='前日比[%]')
data_To_NS = convert_2dim4dist(df_toyota, df_NipponSteel, column='前日比[%]')
print(f'データ形状: {data_To_Ni.shape}')
dist_To_Ni = multi_normaldistribution(data_To_Ni, [mean_toyota, mean_Nissui], cov_To_Ni)
print(f'多変量ガウス分布の確率密度関数:{dist_To_Ni.shape}')[OUT]
データ形状: (489, 2)
多変量ガウス分布の確率密度関数:(489,)6-9.データの可視化
計算の準備が出来ましたのでトヨタ自動車をベンチマークとした前日比の多変量ガウス分布を作成していきます。可視化は①等高線図、②3Dプロットの2種類を作成しました。見やすい・理解しやすい方を使用したらよいと思います。
各プロットにおける設計思想は下記の通りです。
作成したプロット図を保管するための"output"フォルダを作成
x軸、y軸はデータの最大値、最小値から判定して自動で描写(固定値ではない)
設定に応じて、渡したデータを散布図としてプロット
カラーバーは設置、等高線(plt.clabel)は非表示
ラベルの追加、画像の保存、グリッド表示などはフラグで調整
[IN]
if not os.path.exists('output'): os.mkdir('output') #outputディレクトリがなければ作成
def plot_contour(data, mean, cov, original_data=None, labels:List=None, save:bool=False, verbose:bool=False):
x_min, x_max = data[:, 0].min() - 0.05, data[:, 0].max() + 0.05 #X軸の範囲:最小値-0.05~最大値+0.05
y_min, y_max = data[:, 1].min() - 0.05, data[:, 1].max() + 0.05 #Y軸の範囲:最小値-0.05~最大値+0.05
# グリッドを作成
x = np.linspace(x_min, x_max, 100)
y = np.linspace(y_min, y_max, 100)
X, Y = np.meshgrid(x, y) #メッシュグリッドを作成(3次元配列用)
XY = np.stack([X, Y], axis=-1) #メッシュグリッドを作成(2次元配列用)
# 確率密度関数の値を計算
prob_density = multi_normaldistribution(XY, mean, cov) #確率密度関数の値を計算
# グラフを描画
fig = plt.figure(figsize=(10, 5), facecolor='white')
# 等高線プロット
plt.contourf(X, Y, prob_density, cmap='rainbow') #cmapの種類|bwr:青-白-赤, rainbow:虹色
plt.colorbar(label='Probability density') # カラーバーのラベルを表示
# plt.clabel(plt.contour(X, Y, prob_density, colors='k')) # 等高線を表示
if original_data is not None:
plt.scatter(original_data[:, 0], original_data[:, 1], color='grey', marker='o', s=2, alpha=0.3)
if labels:
plt.xlabel(f'{labels[0]}の前日比[%]'), plt.ylabel(f'{labels[1]}の前日比[%]')
plt.title(f'多変量ガウス分布:{labels[0]}vs{labels[1]}の前日比', y=-0.20)
else:
plt.xlabel('x1'), plt.ylabel('x2')
plt.title('多変量ガウス分布の等高線図')
if save and labels:
plt.savefig(f'output/contour_{labels[0]}_vs_{labels[1]}.png')
elif save:
plt.savefig('output/contour.png')
if verbose:
plt.grid()
plt.show()
def plot_3d(data, mean, cov, original_data=None, labels: List = None, save: bool = False, verbose: bool = True):
x_min, x_max = data[:, 0].min() - 0.05, data[:, 0].max() + 0.05
y_min, y_max = data[:, 1].min() - 0.05, data[:, 1].max() + 0.05
# グリッドを作成
x = np.linspace(x_min, x_max, 100)
y = np.linspace(y_min, y_max, 100)
X, Y = np.meshgrid(x, y)
XY = np.stack([X, Y], axis=-1)
# 確率密度関数の値を計算
prob_density = multi_normaldistribution(XY, mean, cov)
# 3Dプロット
fig = plt.figure(figsize=(10, 10), facecolor='white')
ax = fig.add_subplot(111, projection='3d') #3Dプロット用のサブプロットを作成
cmap = 'coolwarm' #cmapの種類|coolwarm:青-白-赤, viridis:黄-緑-青
ax.plot_surface(X, Y, prob_density, alpha=0.7, cmap=cmap) #3Dプロットを作成
if verbose:
fig = plt.colorbar(ax.plot_surface(X, Y, prob_density, alpha=0.7, cmap=cmap), shrink=0.5, aspect=5) #カラーバーを表示
if original_data is not None:
Z = multi_normaldistribution(original_data, mean, cov)
ax.scatter(original_data[:, 0], original_data[:, 1], Z, color='green', marker='o', s=10, alpha=0.3)
if labels:
ax.set_xlabel(f'{labels[0]}の前日比[%]'), ax.set_ylabel(f'{labels[1]}の前日比[%]'), ax.set_zlabel('Probability Density')
ax.set_title(f'多変量ガウス分布: {labels[0]} vs {labels[1]}', y=-0.10)
else:
ax.set_xlabel('x1'), ax.set_ylabel('x2'), ax.set_zlabel('Probability Density')
ax.set_title('多変量ガウス分布の3Dプロット')
plt.show() 参考としてNotebook使用時に「%matplotlib inline」を使用するとIDE内にプロット図が表示され、「%matplotlib qt」を使用すると別ウィンドウで図が確認できます。
%matplotlib qtを使用するとインタラクティブとなるため3Dプロットを回転させてみたいときには便利です。

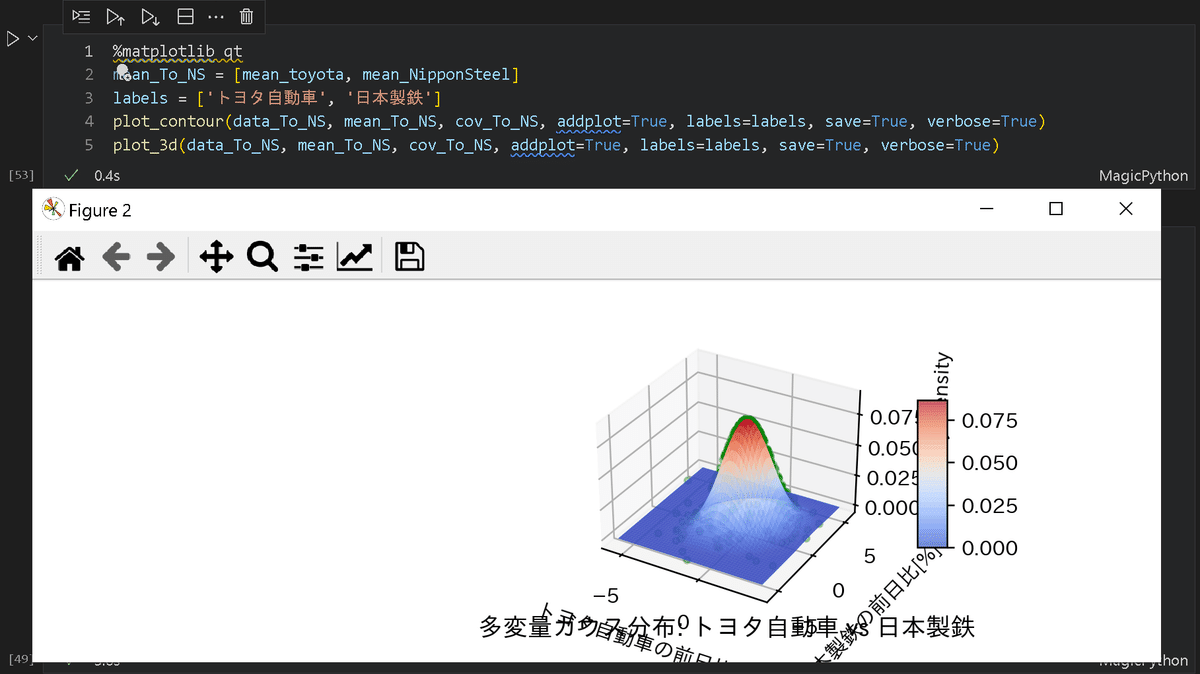
6-9-1.トヨタ(自動車)vs日本製鉄(鉄鋼)
まずはトヨタと日本製鉄を確認しました。結果は下記の通りです。
全体的に右上がりの分布のため小さな正の相関が確認できる。つまり、セクター間に相関関係がありポートフォリオ的には問題ないと判断できる。
多変量ガウス分布全体の分散が大きいため前日比だけで判断は難しい。
分散の確認方法として、条件付き確率分布$${P(Y|X)}$$があります。これは片方の次元を固定した時の多次元側の平面となります(xの値を固定した時はy-z平面)。なお特徴で説明の通り「多変量ガウス分布の条件付き確率も多変量ガウス分布」になります。
トヨタの前日比=0%の時の確率分布$${P(r_{日本製鉄}|r_{Toyota}=0)}$$より、日本製鉄の前日比は0±2.7%程度変化しておりばらつきは大きい
トヨタの前日比=2%の時の確率分布$${P(r_{日本製鉄}|r_{Toyota}=2)}$$より、日本製鉄の前日比は1±1.3%程度変化している。つまりトヨタの前日比が高い時は日本製鉄も高くなる確率が高い。
確率密度は各次元ともに-1~1%程度のエリアに集中(赤, 橙色のエリア)している。つまり、確率的には大きな価格変動(ボラティリティ)はなく、安定的な株と判断できる。
[IN]
mean_To_NS = [mean_toyota, mean_NipponSteel]
labels = ['トヨタ自動車', '日本製鉄']
plot_contour(data_To_NS, mean_To_NS, cov_To_NS, addplot=True, labels=labels, save=True, verbose=True)
plot_3d(data_To_NS, mean_To_NS, cov_To_NS, addplot=True, labels=labels, save=True, verbose=True)
[OUT]



6-9-2.トヨタ(自動車)vsニッスイ(食品)
トヨタとニッスイを確認しました。結果は下記の通りです。
日本製鉄と異なり、全体的な分布が水平に近い分布であり、相関が小さいと判断できます。
強気の投資をしたいのであれば、相関関係が小さいためポートフォリオとしては不適です。
保守的な投資(低リスク)をしたい場合、分布的に負の相関は見られないため分散投資としては問題ありません。今回のケースでは自動車セクターがダメだった時のリスクヘッジにはなりますが、逆に自動車セクターが好調の時によい結果は得られません。
相関関係が小さい、つまり各セクターは独立なため指標としては使用しにくい。
確率密度は各次元ともに-1~1%程度のエリアに集中(赤, 橙色のエリア)している。つまり、確率的には大きな価格変動(ボラティリティ)はなく、安定的な株と判断できる。
[IN]
mean_To_Ni = [mean_toyota, mean_Nissui]
labels = ['トヨタ自動車', 'ニッスイ']
plot_contour(data_To_Ni, mean_To_Ni, cov_To_Ni, addplot=True, labels=labels, save=True, verbose=True)
plot_3d(data_To_Ni, mean_To_Ni, cov_To_Ni, addplot=True, labels=labels, save=True, verbose=True)
[OUT]

6-9-3.トヨタ(自動車)vsENEOS(エネルギー)
トヨタとENEOSを確認しました。結果は下記の通りです。
やや右上がりの分布であり小さな正の相関が確認できる。ただし日本製鉄ほどではないため、ポートフォリオに入れる場合はリスクヘッジの意味合いが強くなると判断できる。
確率密度は各次元ともに-1~1%程度のエリアに集中(赤, 橙色のエリア)している。つまり、確率的には大きな価格変動(ボラティリティ)はなく、安定的な株と判断できる。
[IN]
mean_To_Ene = [mean_toyota, mean_Eneos]
labels = ['トヨタ自動車', 'エネオス']
plot_contour(data_To_Ene, mean_To_Ene, cov_To_Ene, addplot=True, labels=labels, save=True, verbose=True)
plot_3d(data_To_Ene, mean_To_Ene, cov_To_Ene, addplot=True, labels=labels, save=True, verbose=True)
[OUT]
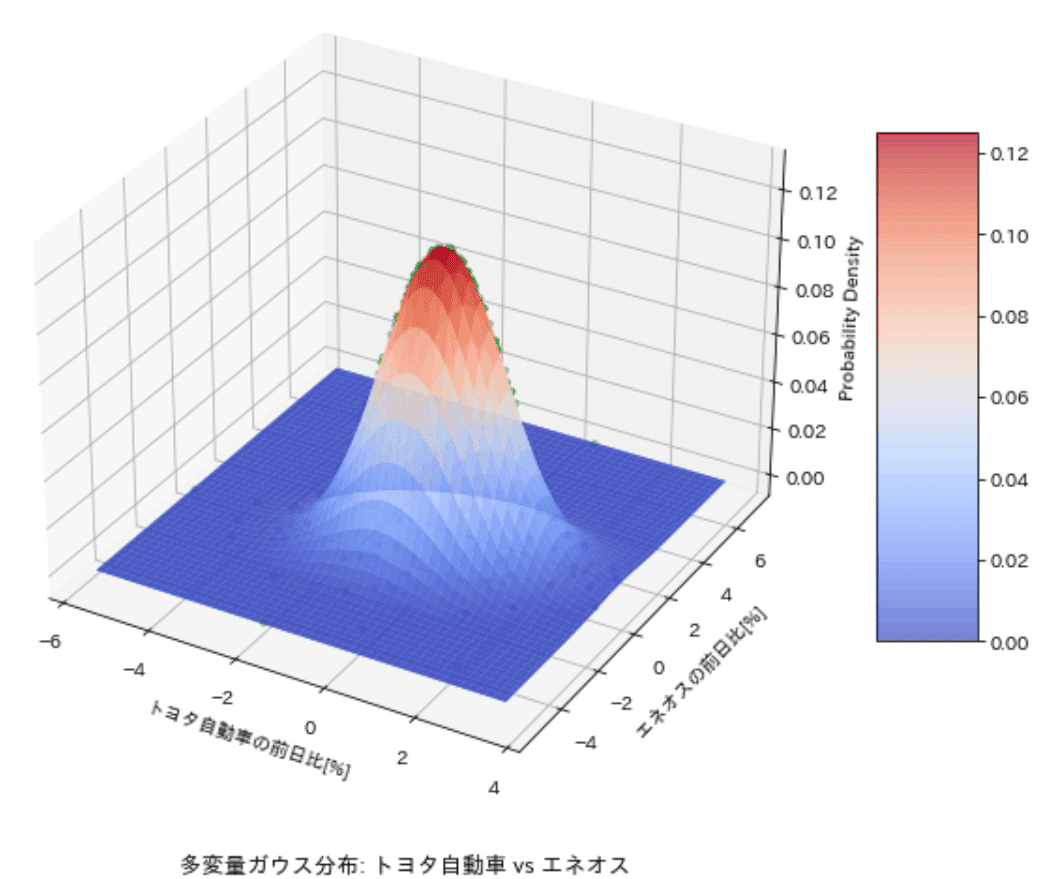
6-9-4.トヨタ(自動車)vs武田(医薬品)
トヨタと武田薬品工業を確認しました。結果は下記の通りです。
やや右上がりの分布であり小さな正の相関が確認できる。ただし日本製鉄ほどではないため、ポートフォリオに入れる場合はリスクヘッジの意味合いが強くなると判断できる。
確率密度は各次元ともに-1~1%程度のエリアに集中(赤, 橙色のエリア)している。つまり、確率的には大きな価格変動(ボラティリティ)はなく、安定的な株と判断できる。
[IN]
mean_To_Ta = [mean_toyota, mean_Takeda]
labels = ['トヨタ自動車', '武田薬品']
plot_contour(data_To_Ta, mean_To_Ta, cov_To_Ta, addplot=True, labels=labels, save=True, verbose=True)
plot_3d(data_To_Ta, mean_To_Ta, cov_To_Ta, addplot=True, labels=labels, save=True, verbose=True)
[OUT]

7.別添
7-1.コラム:分散共分散行列の行列(X^TX)
重回帰分析で説明変数$${\bf X}$$に対して出てくる$${\bf X^TX}$$は「データセットの平均が0の時の分散共分散行列」と近い値になります。式変換で確認してみました。
$${N}$$:データ数(行数)、$${M}$$:次元数(特徴量)、$${\bf x}$$は縦ベクトルとしたため横ベクトルは転置$${\bf x^T}$$としました。また$${X(i,:)}$は行列$${X}$$のi番目の行ベクトルとします。
$$
\begin{aligned}
{\bf X} &
= \begin{bmatrix} x_{10} & x_{11} & x_{12} & \cdots & x_{1M} \\
x_{20} & x_{21} & x_{22} & \cdots & x_{2M} \\
x_{30} & x_{31} & x_{32} & \cdots & x_{3M} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
x_{N0} & x_{N1} & x_{N2} & \cdots & x_{NM} \end{bmatrix}
=\begin{bmatrix} \bf x_{1} & \bf x_{2} & \bf x_{3} & \cdots & \bf x_{M} \end{bmatrix}
\end{aligned}
$$
$$
\begin{aligned}
{\bf X^T} = \begin{bmatrix} x_{10} & x_{20} & x_{30} & \cdots & x_{N0} \\
x_{11} & x_{21} & x_{31} & \cdots & x_{N1} \\
x_{12} & x_{22} & x_{32} & \cdots & x_{N2} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
x_{1M} & x_{2M} & x_{3M} & \cdots & x_{NM} \end{bmatrix}
=\begin{bmatrix}{\bf x}_1^{\rm T}\\{\bf x}_2^{\rm T} \\{\bf x}_3^{\rm T} \\\vdots \\{\bf x}_M^{\rm T}\end{bmatrix}
=\begin{bmatrix}{\bf X(1,:)}\\{\bf X(2,:)} \\{\bf X(3,:)} \\\vdots \\{\bf X(M,:)}\end{bmatrix}
\end{aligned}
$$
$$
\begin{aligned}
\bf X^T X
&=\begin{bmatrix}{\bf x}_1^{\rm T}\\{\bf x}_2^{\rm T} \\{\bf x}_3^{\rm T} \\\vdots \\{\bf x}_M^{\rm T}\end{bmatrix} \begin{bmatrix} \bf x_{1} & \bf x_{2} & \bf x_{3} & \cdots & \bf x_{M} \end{bmatrix}
\\&=\begin{bmatrix} x_{10} & x_{20} & x_{30} & \cdots & x_{N0} \\
x_{11} & x_{21} & x_{31} & \cdots & x_{N1} \\
x_{12} & x_{22} & x_{32} & \cdots & x_{N2} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
x_{1M} & x_{2M} & x_{3M} & \cdots & x_{NM} \end{bmatrix}
\begin{bmatrix} x_{10} & x_{11} & x_{12} & \cdots & x_{1M} \\
x_{20} & x_{21} & x_{22} & \cdots & x_{2M} \\
x_{30} & x_{31} & x_{32} & \cdots & x_{3M} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
x_{N0} & x_{N1} & x_{N2} & \cdots & x_{NM} \end{bmatrix}
\end{aligned}
$$
まず参考で①対角要素の内積、②対角以外の内積を計算してみます。
【対角要素:$${\bf X^T}$$:1行目、$${\bf X}$$:1列目】
$$
\begin{aligned}
\bf x_{1}^T\bf x_{1} &= \begin{bmatrix} x_{10} & x_{20} & x_{30} & \cdots & x_{N0} \end{bmatrix}
\begin{bmatrix} x_{10} \\ x_{20} \\ x_{30} \\ \vdots \\ x_{N0} \end{bmatrix}
\\&= x_{10}x_{10} + x_{20}x_{20} + x_{30}x_{30} + \cdots + x_{N0}x_{N0}
\\&= x_{10}^2 + x_{20}^2 + x_{30}^2 + \cdots + x_{N0}^2
\\&=\sum_{i=1}^Nx_{i0}^2
\end{aligned}
$$
【対角要素以外:$${\bf X^T}$$:1行目、$${\bf X}$$:$${3}$$列目】
$$
\begin{aligned}
\bf x_{1}^T\bf x_{3} &= \begin{bmatrix} x_{10} & x_{20} & x_{30} & \cdots & x_{N0} \end{bmatrix}
\begin{bmatrix} x_{12} \\ x_{22} \\ x_{32} \\ \vdots \\ x_{N2} \end{bmatrix}
\\&= x_{10}x_{12} + x_{20}x_{22} + x_{30}x_{32} + \cdots + x_{N0}x_{N2}
\\&=\sum_{i=1}^N x_{i0}x_{i2}
\end{aligned}
$$
これより数式は下記の通りとなります。
$$
\begin{aligned}
\bf X^T X &=\begin{bmatrix}{\bf x}_1^{\rm T}\\{\bf x}_2^{\rm T} \\{\bf x}_3^{\rm T} \\\vdots \\{\bf x}_M^{\rm T}\end{bmatrix} \begin{bmatrix} \bf x_{1} & \bf x_{2} & \bf x_{3} & \cdots & \bf x_{M} \end{bmatrix} \\&= \begin{bmatrix}\sum_{i=1}^Nx_{i0}^2 & \sum_{i=1}^N x_{i0}x_{i1} &\sum_{i=1}^N x_{i0}x_{i2} & \cdots & \sum_{i=1}^N x_{i0}x_{iM} \\
\sum_{i=1}^N x_{i1}x_{i0} & \sum_{i=1}^Nx_{i1}^2 &\sum_{i=1}^N x_{i1}x_{i2} & \cdots &\sum_{i=1}^N x_{i1}x_{iM} \\
\sum_{i=1}^N x_{i2}x_{i0} & \sum_{i=1}^N x_{i2}x_{i1} & \sum_{i=1}^Nx_{i2}^2& \cdots & \sum_{i=1}^N x_{i2}x_{iM} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
\sum_{i=1}^N x_{iM}x_{i0} & \sum_{i=1}^N x_{iM}x_{i1} & \sum_{i=1}^N x_{iM}x_{i2} & \cdots & \sum_{i=1}^Nx_{iM}^2 \end{bmatrix}
\end{aligned}
$$
平均値が0の場合、分散・共分散は下記の通りとなるため$${\bf X^TX}$$は「データセットの平均が0の時の分散共分散行列」と近い概念を表していることが確認できます。
$$
(標本)分散\sigma^2 = \frac{1}{n}\sum_{i=1}^{n} (x_i - \bar{x})^2=\frac{1}{n}\sum_{i=1}^{n} x_i^2
$$
$$
共分散{{\rm Cov}(X,Y)} = \frac{1}{n}\sum_{i=1}^{n}(x_i -\bar{x})(y_i - \bar{y})=\frac{1}{n}\sum_{i=1}^{n}x_iy_i
$$
参考資料
あとがき
将来的には株価データからAIを用いた自動売買ツールを作成予定です。
この記事が気に入ったらサポートをしてみませんか?
