Pythonでやってみた(Engineering):方程式の数値解法/ニュートン・ラフソン法
1.概要
方程式の解法において、数式の変形による解が得られない場合は数値計算を使用して計算します。本記事では「方程式の数値解法」として「ニュートン法(ニュートン・ラフソン法)」を紹介します。
※数値解法として2分法という簡単なアルゴリズムもありますが収束速度が1次のため、求め方が粗く計算回数がかかります。ニュートン法は2次のため計算回数が少なくて済むので速度が速い特徴があります。
2.ニュートン法アルゴリズムの理解
ニュートン法では関数f(x)において、f(x)=0となるxを数値計算で求めることが出来ます。原理としては、①f(x)の微分によりx軸との交点から近似値を算出、②計算条件を満たしているか判定 を繰り返し計算することで真値に近づけていきます。
$$
ニュートン法におけるx_{n}の次の近似解:x_{n+1} = x_{n} - \frac{f(x_{n}) }{f'(x_{n}) }
$$
$$
計算条件の判定:|x_{n+1} - x_{n} |<閾値(適当に小さい数値を設定)
$$
サンプルとして下記数値を扱います。下記の通り手計算で確認するとf(x)=0となるx=1.16です。こちらを数値計算で求めます。
$$
f(x) =x^2+4x-6= (x+2)^2 - 10
$$
$$
f'(x) =\frac{f(x+h)-f(x)}{h} =\frac{(x^2+2hx+h^2+4x+4h-6)-(x^2+4x-6)}{h}= 2x+4
$$
$$
f(x)=0の場合、x=\sqrt10 - 2 = 1.1623
$$

2-1.ニュートン法の近似値xの算出方法
関数$${f(x)}$$があり初期値$${x_{0}}$$における$${y=f({x_{0}})}$$となります。この$${f({x_{0}})}$$における傾きからx軸との交点(y=0)を計算してこの交点の値を$${x_{1}}$$とすると、この$${x_{1}}$$は真値に近づきます。
$$
f'(x_{0}) = \frac{f(x_{0})-0}{x_{0}-x_{1}}よりx_{1}=x_{0}- \frac{f(x_{0})}{f'(x_{0})}
$$
$$
ニュートン法におけるx_{n}の次の近似解:x_{n+1} = x_{n} - \frac{f(x_{n}) }{f'(x_{n}) }
$$
例として$${f(x)=(x+2)^2-10}$$でニュートン法の動作を確認します。


2-2.ニュートン法における収束条件
ニュートン法における収束条件は下記の通りです。
絶対的な収束条件は$${f'(x)\neq0}$$である。:傾きが0だとx軸との接点を見つけることが出来ないため
$${f(x)=0}$$の条件が存在すること:下図の通り$${f(x)=0}$$の条件が存在しない場合、①極小値付近まで近づく、②極小値付近$${f'(x)\fallingdotseq0}$$になり値が発散します。

収束条件の判定は$${x_{n+1} = x_{n} - \frac{f(x_{n}) }{f'(x_{n}) }}$$より近似値との誤差$${|x_{n+1}-x_{n}|}$$が特定に値以下になるまで計算します。

3.Pythonによる関数化(コード)
それではPythonで実装します。まず初めに使用するライブラリをインポートしておきます。
[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib3-1.数値微分:numerical differentiation
ニュートン法では傾きを求めるために微分が必要です。簡単に求める方法として数値微分を実装します。
一般的な微分は前方差分ですがPythonでそのまま実装するとhの値次第で真の傾きからずれる可能性があります。hを限りなく小さくすると解消できますがその場合は丸め誤差(rounding error)の問題が発生します。
そこで誤差を小さくするために中心差分で実装します。
$$
前方差分:\frac{df(x)}{dx}=\lim_{h\to 0} \frac{f(x+h)-f(x)}{h}
$$
$$
中心差分:\frac{df(x)}{dx}=\lim_{h\to 0} \frac{f(x+h)-f(x-h)}{2h}
$$
[IN]
def numerical_diff(f, x):
h = 1e-4 #丸め誤差が出ない程度の小さな値
return (f(x+h) - f(x-h)) / (2*h)
def func_text(x):
return x**2 + 2
numerical_diff(func_text, 3)
[OUT]
6.000000000012662サンプルは$${f(x)=x^2+2}$$より$${f’(x)=2x}$$なのでx=3であれば$${f’(3)=6}$$ですが近い値となっております。なお、hを小さくすると精度は高くなりますが過剰に小さくすると丸め誤差の影響で正しい値がでなくなるため注意が必要です。
[IN ※エラー例]
def numeriacal_diff(f, x, i):
h = 1/10**i #丸め誤差が出ない程度の小さな値
return (f(x+h) - f(x-h)) / (2*h)
def func_text(x):
return x**2 + 2
output=[]
for i in range(21):
y = numeriacal_diff(func_text, 3, i)
output.append([f'1e-{i}', y])
df = pandas.DataFrame(output, columns=['h', 'f(x)'])
columns= df['h']
df_T = df.T
df_T.columns = columns
df_T.loc[['f(x)']]
[OUT]
1e-12あたりから値が安定しなくなっており1e-16以降では値が0になる
3-2.ニュートン法の実装
2章で説明した通りニュートン法は下記2つで構成されます。
$${x_{n+1} = x_{n} - \frac{f(x_{n}) }{f'(x_{n}) }}$$より近似値を算出
計算条件を判定して閾値以下になるまで繰り返し計算
それぞれの機能を一つのオブジェクトにまとめたいためクラスで作成します。なお細かいところで下記機能追加しました。
verbose(Bool)でループ回数の確認が可能
max_iterでループ回数の上限を設定することで無限ループ防止
[IN]
class NewtonMethod:
def __init__(self, func, verbose=False):
self.func = func
self.verbose = verbose
def predict_approxvalue(self, x):
x_next = x - self.func(x) / numeriacal_diff(self.func, x)
return x_next
def __call__(self, x0, thresh=1e-6, max_iter=10000):
count = 0 #iteration回数
#初期化
x1 = self.predict_approxvalue(x0)
error = np.abs(x1 - x0) #絶対値誤差
#Loop
while error>thresh and count<max_iter:
x0 = x1
x1 = self.predict_approxvalue(x0)
error = np.abs(x1 - x0)
count += 1
if self.verbose:
return x1, count
else:
return x1
#関数f(x)
def f(x):
return (x+2)**2 - 10
newtonmethod = NewtonMethod(f, verbose=True)
newtonmethod(8)
[OUT]
(1.1622776601683795, 5)サンプルは$${f(x)=(x+2)^2-10}$$より$${f(x)=0}$$での$${x=\sqrt10-2=1.162}$$です。今回の結果では適当に$${x_{0}=8}$$から始めましたが5回の計算で解を取得することが出来ました。

3-3.全コード:ニュートン法
使用したコードを記載します。今までは説明としてxの初期値をx=8として手動で入力しておりましたが実際に使用する時は(発散しなければ)不要のためnp.random.rand()で初期値x0=0~1に自動調整するようにしました。
発散した場合は初期値を手動で調整することも可能です。
[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
def numeriacal_diff(f, x):
h = 1e-4 #0.0001
return (f(x+h) - f(x-h)) / (2*h)
class NewtonMethod:
def __init__(self, func, verbose=False):
self.func = func
self.verbose = verbose
def predict_approxvalue(self, x):
x_next = x - self.func(x) / numeriacal_diff(self.func, x)
return x_next
def __call__(self, x0=None, thresh=1e-6, max_iter=10000):
count = 0 #iteration回数
if x0 is None:
x0 = np.random.rand(1).__float__() #最初の傾きを決めるためのxの初期値
#初期化
x1 = self.predict_approxvalue(x0)
error = np.abs(x1 - x0) #絶対値誤差
#Loop
while error>thresh and count<max_iter:
x0 = x1
x1 = self.predict_approxvalue(x0)
error = np.abs(x1 - x0)
count += 1
if self.verbose:
return x1, count
else:
return x1
#関数f(x)
def f(x):
return (x+2)**2 - 10
newtonmethod = NewtonMethod(f, verbose=True)
print(newtonmethod(x0=8))
newtonmethod2 = NewtonMethod(f, verbose=True)
print(newtonmethod2())
[OUT]
(1.1622776601683795, 5)
(1.162277660168379, 3)3-4.全コード:可視化関係(参考用)
ニュートン法とは関係ないですが、今回の記事を作成するために作成した可視化用コードも記載しておきます。
可視化用ではループにおける各iterationの出力が欲しいためループ計算はNewtonMethodクラスは使用せず個別でコード作成しました。
[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
x = np.linspace(-10, 10, 100) #-10から10まで100個の等間隔な値を生成
colors = {0:'b', 1:'g', 2:'r', 3:'c', 4:'m', 5:'y', 6:'k', 7:'b'}
#関数f(x)
def f(x):
return (x+2)**2 - 10
x0 = 8
x1 = x0 - f(x0) / numeriacal_diff(f, x0) #x1=8-90/20=3.5
#matplotlibの設定/表示用関数
plt.rcParams['font.size'] = 14
fig = plt.figure(figsize=(12, 6))
ax = fig.add_subplot(111)
ax.plot(x, f(x), label='f(x)', color='black', lw=1.)
ax.plot(x, np.zeros(x.shape), label='y=0', color='black', lw=1.)
ax.plot((8,8), (0, f(8)), label='f(x0)', color='blue', lw=1., ls='dashed')
ax.plot((x0,x1), (f(x0), 0), label="f'(x0)", color='blue', lw=1., ls='dashed')
ax.set(title='初期値x0における接線およびx軸との交点x1',
xlabel='x', ylabel='f(x)',
xticks=np.arange(min(x), max(x)+1, 2.0), xlim=(min(x), max(x)))
ax.text(x0, -5, f'x{0}={x0:.1f}', color='blue', fontsize=14)
ax.text(8, f(8)+10, "f'(x)", fontsize=14, color='blue')
ax.patch.set_facecolor('white') #背景色を白
plt.grid()
plt.legend()
newtonmethod = NewtonMethod(f, verbose=True)
max_iter = 6
#matplotlibの設定/表示用関数
plt.rcParams['font.size'] = 14
fig = plt.figure(figsize=(18, 8))
ax = fig.add_subplot(111)
ax.plot(x, f(x), label='f(x)', color='black', lw=1.)
ax.plot(x, np.zeros(x.shape), label='y=0', color='black', lw=1.)
count = 0 #iteration回数
x0=8
thresh=1e-6
#初期化
x1 = newtonmethod.predict_approxvalue(x0)
error = np.abs(x1 - x0) #絶対値誤差
#Loop
while error>thresh and count<max_iter:
ax.plot((x0,x0), (0, f(x0)), label=f'x{count}={x0:.2f}', color=colors[count], lw=1., ls='dashed')
ax.plot((x0,x1), (f(x0), 0), label=f"'(x{count})", color=colors[count], lw=1., ls='dashed')
ax.text(x0, -5, f'x{0}={x0:.2f}', color=colors[count], fontsize=14)
ax.text(x0, f(x0)+10, f"'(x{count})", fontsize=14, color=colors[count])
x0 = x1
x1 = newtonmethod.predict_approxvalue(x0)
error = np.abs(x1 - x0)
count += 1
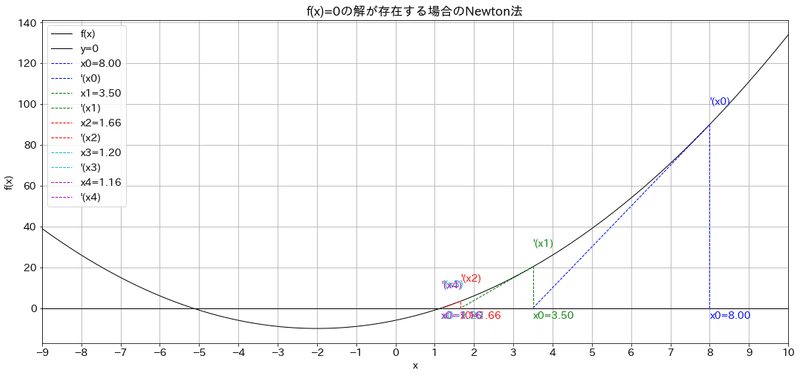
ax.set(title='f(x)=0の解が存在する場合のNewton法',
xlabel='x', ylabel='f(x)',
xticks=np.arange(-9, 10+1, 1.0), xlim=(-9, 10))
ax.patch.set_facecolor('white') #背景色を白
plt.grid()
plt.legend(loc='upper left')
[OUT]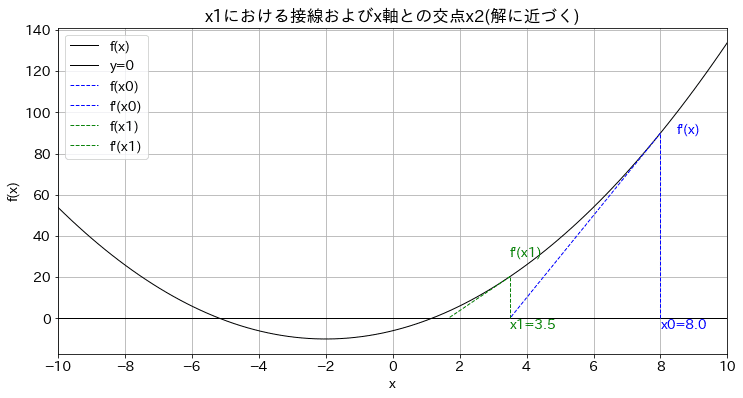
4.ライブラリでの実装:Scipy
便利なライブラリとしてScipy.optimizeのroot_scalarが使用可能です。Newton法を使用する場合は目的関数だけでなくfprime引数に導関数(微分した式)を与える必要があります。
[API]
scipy.optimize.root_scalar(f, args=(), method=None, bracket=None,
fprime=None, fprime2=None, x0=None, x1=None,
xtol=None, rtol=None, maxiter=None, options=None)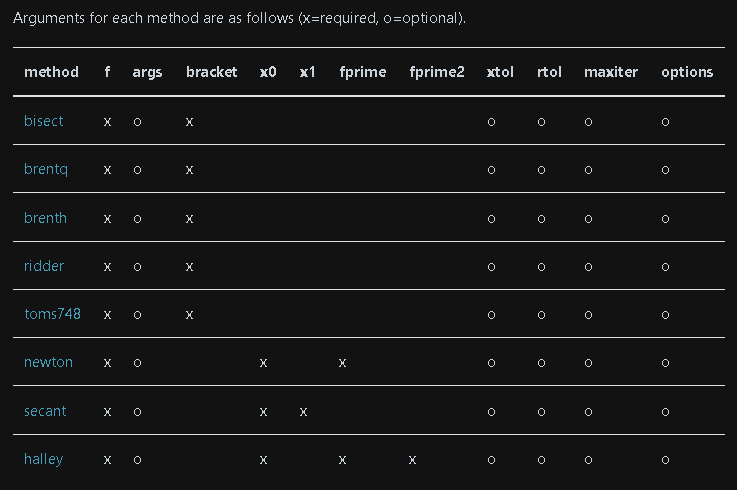
[IN]
def numeriacal_diff_f(x):
h = 1e-4 #0.0001
return (f(x+h) - f(x-h)) / (2*h)
solver = root_scalar(f, fprime=numeriacal_diff_f, method='newton', x0=8)
print(solver)[OUT]
converged: True
flag: 'converged'
function_calls: 12
iterations: 6
root: 1.1622776601683793導関数として数値微分の関数を渡しても動作可能です。
[IN]
def numeriacal_diff_f(x):
h = 1e-4 #0.0001
return (f(x+h) - f(x-h)) / (2*h)
solver = root_scalar(f, fprime=numeriacal_diff_f, method='newton', x0=8)
print(solver)[OUT]
converged: True
flag: 'converged'
function_calls: 12
iterations: 6
root: 1.1622776601683795参考記事
あとがき
機械学習も勉強したいけど基礎的なところも押さえておかないといざというときに何もできなくなりそうなので、こういうのも学びなおしたい
この記事が気に入ったらサポートをしてみませんか?
