【適切な推計のためのデータ処理📝】『Japanese Foreign Exchange Interventions, 1971-2018:Estimating a Reaction Function Using the Best Proxy』:先行研究解説 No.9💝2023/10/23
Introduction:卒業論文は早めに仕上げたい💛
私もいよいよ卒業論文の執筆に
取りかかる時期がやって参りました👍
何事もアウトプット前提のインプットが
大事であると、noteで毎日発信してきました
これは、どのような内容で
あっても当てはまります👍
論文を一概に読んでも
記憶に残っていなかったり
大切な観点を忘れてしまっていたりしたら
卒業論文の進捗は滞ってしまうと思います
だからこそ、この「note」をフル活用して
卒業論文を1%でも
完成に向けて進めていきたいと思います
私の卒論執筆への軌跡を
どうぞご愛読ください📖
今回の参考文献🔥
今回、読み進めていく論文は
こちらのURLになります👍
『Japanese Foreign Exchange Interventions, 1971-2018: Estimating a Reaction Function Using the Best Proxy』
Takatoshi Ito(a), Tomoyoshi Yabu(b)
(a) School of International and Public Affairs, Columbia University, and GRIPS, Tokyo
(b) Department of Business and Commerce, Keio University
読み終えた先行研究📚
『日本の為替介入の分析』 伊藤隆敏・著
経済研究 Vol.54 No.2 Apr. 2003
『Effects of the Bank of Japan’s intervention on yen/dollar exchange rate volatility』21 November 2004
Toshiaki Watanabe (a), Kimie Harada(b)
『The Effects of Japanese Foreign Exchange Intervention: GARCH Estimation and Change Point Detection』
Eric Hillebrand Gunther Schnabl Discussion
Paper No.6 October 2003
Japanese Foreign Exchange Interventions, 1971-2018: Estimating a Reaction Function Using the Best Proxy
December 12, 2019
Takatoshi Ito(a), Tomoyoshi Yabu(b)
(a) School of International and Public Affairs, Columbia University, and GRIPS, Tokyo
(b) Department of Business and Commerce, Keio University
前回のお復習い📝
3.3. Important adjustments in the test
Let us denote interventions conducted during the last two business days of the month by Int_t^End.
These amounts are recorded in the fiscal accounts that are used in the monthly proxy of month t+1.
Similarly, Int_t+1^End is recorded in the monthly proxy of month t.
Thus, the proxy of month t should be compared against settlement-based intervention amounts, calculated as:
Int_t^End によって月の最後の 2 営業日の間に行われた介入額が示されます
これらの金額は、t+1月の月次代理変数(Proxy)で使用される会計口座に記録されます📝
同様に、Int_t+1^Endは、t 月の月次代理変数に記録されます
したがって、t 月の代理額は、次のように計算された取引ベースの介入金額(settlement-based intervention amounts)と比較される必要があるのです
$$
\\Proxy\\
Int_t^{Settlement}=Int_t -(Int_t^{End}-Int_{t-1}^{END})
$$
In order to see the point of this discussion, the estimated errors of the best proxy ( Error= Int_t - Proxy_t) are examined.
We argue that this is mostly explained by the end-of-month interventions and the t+2 difference between transaction and settlement. We define the t+2 difference as EoMDifft (abbreviation of “end of month difference”):
この議論の要点を理解するために、最良の代理変数の推定誤差 (Error= Int_t - Proxy_t) を調べます
これは、月末の介入と取引ベース間の決済日数のラグである t+2日後という差によって主に説明されるという主になりります
そして決済 t+2 の差を EoMDifft (「月末の差」の略語) として定義しています
$$
EoMDiff_t =Int_t^{End}-Int_{t-1}^{End}
$$
Fig. 2 shows the time series of Errort and EoMDifft where Errort is again computed using “Adjusted MOF FEEF” as a proxy.
As expected, the “Errors” appear to be explained mostly as a result of end-of-month interventions and the t+2 settlement.
To be statistically accurate, a regression is conducted:
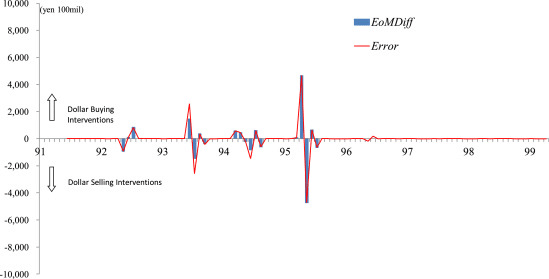
図2は、Error_tとEoMDiff_tの時系列を示しています
Error_tは「調整済み MOF FEEF」が代理変数(Prixy)として使用され、再度計算されています
予想どおり、「エラー」は主にt+2 決済ルールに基づく月末の介入の結果として説明されるようです
統計的に正確にするために、以下の回帰を実行することにします
$$
Error_t =-8.200+1.074 EoMDiff_t \\
s.e (7.166) (0.083)\\ \\R^2=0.956
$$
Here HAC standard errors are in brackets.
Neither H0: β0= 0 nor H0: β1= 1 is rejected; the deviation of the proxy from transaction-based interventions is well explained by the end-of-month interventions.
In fact, 95.6% of the deviation is due to end-of-month interventions, as shown by R^2 = 0.956.
ここで、HAC標準誤差の値は、括弧内に示されています
推計結果より、帰無仮説「H0: β0= 0」も「H0: β1= 1」も棄却されませんでした
決済ベースの介入からの代理変数の偏差は、月末介入によって十分に説明されます
実際のところ、このモデルの決定係数R^2は、0.956で示されるように、この回帰式で説明される被説明変数の変動のうち、95.6%は月末介入(説明変数)による変動であるということが言えるのです
We further examine how close settlement-based intervention data are to various proposed proxies for the period after the disclosure, April 1991.
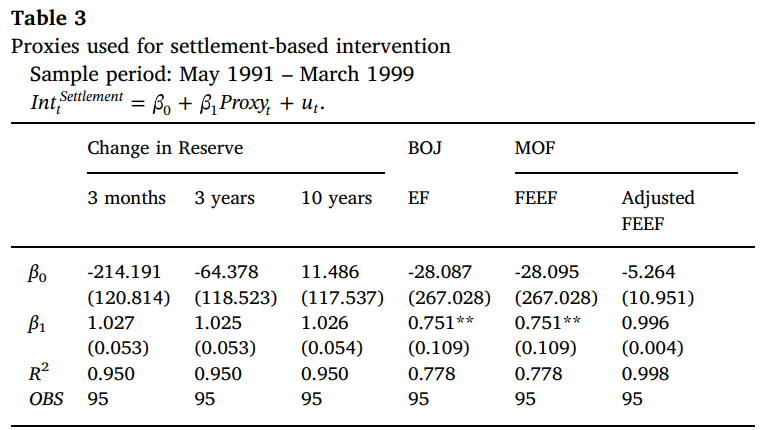
Table 3 shows the regression results of Eq. (1) with the dependent variable being settlement-based interventions ( Int_t^Settlement). As shown, the explanatory power of proxies is much improved, compared to the one in Table 2.
For the regression using “Adjusted MOF FEEF,” the R2 improves from 0.969 in Table 2 to 0.998 in Table 3.3 This is a confirmation that the proxy is an accurate measure, explaining 99.8% of the movements of settlement-based interventions.
さらに、決済ベースの介入(settlement-based intervention)データが、公式データ開示後の1991年4月のさまざまな代替変数の案にどれだけ近いかを調査します
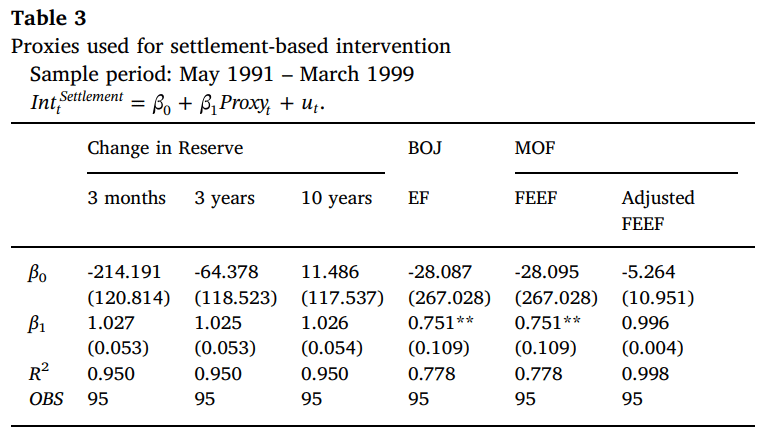
また表3は、回帰式(1)の推計結果を示しています
また回帰式(1)の従属変数は決済ベースの介入 ( Int_t^Settlement ) となります
表3で示されているように、代理変数(prixies)の説明力は、表2のものと比較して大幅に向上していることがわかります
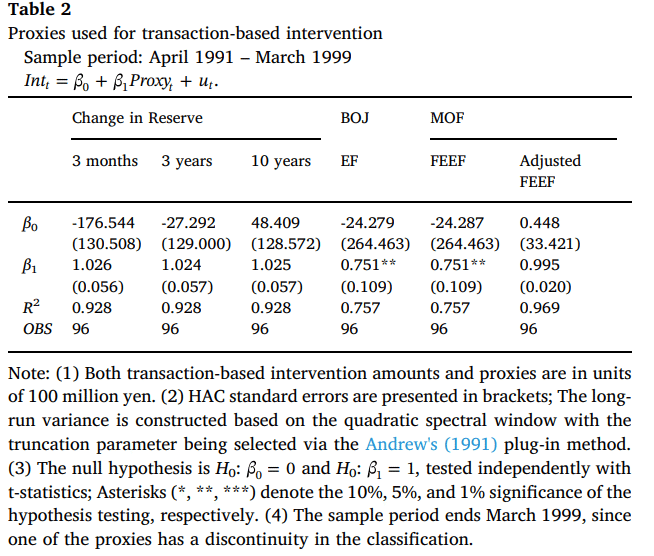
また「調整された MOF FEEF」を使用した回帰では、モデルの決定係数(R^2)は表2の0.969から表3.3の0.998に改善しました👏
これは代理変数(Proxies)が正確な測定値であり、決済ベースの介入の動きの99.8%を説明していることを裏付けていると解釈できるのです
The above detailed examination in search of the best proxy for interventions is thus concluded with both encouraging and discouraging results.
We are encouraged to have found that “Adjusted MOF FEEF” is the best proxy with 99.8% accuracy.
However, our enthusiasm must be tempered slightly given that this accuracy is measured against settlement-based interventions. Hence, considering that daily data are not available prior to April 1991, the available monthly interventions data for months (t) covers the period from the last two days of month (t-1) to the third-to-last business day of month (t).
したがって、上記で述べていた介入に最適な代替変数を探すための詳細な調査は、大変研究の励みになるような結果とはたまた落胆ような結果の両方で結論づけられたことがわかります 「調整された MOF FEEF」が99.8%の精度を持つ最良の代理変数であることが判明したことは嬉しい結果と言えるのではないでしょうか
しかし、この正確性が決済ベースの介入に対して測定されることを考えると、私たちの熱意は少し制御される必要があります
したがって、1991年4月より前は、調査に対する日次データが入手できないことを考慮すると、第t月における入手可能な月次介入データは、t-1月の最後の2日から月の最後から 3番目の営業日までの期間をカバーしているということになるのです
This may pose a problem in analyzing the effectiveness of interventions or the reaction function of the monetary authorities when intervention actions are concentrated at the end of the month.
However, an adjustment can be applied when such circumstances are suspected based on the volatility of the exchange rate; for example, one can use the exchange rate from the third to-last business day as the monthly exchange rate.
This is what we will do in section 5 when estimating the reaction function of the monetary authorities.
このことは、月末に介入が集中する場合において、介入政策の有効性や金融当局の反応関数を分析する上で問題となる可能性があります
ただし、為替レートの変動に基づいてそのような状況が疑われる場合には、調整が適用される場合があります
たとえば、3 営業日から最終営業日までの為替レートを月次為替レートとして使用可能です
これは、後述するセクション5において金融当局の反応関数を推定するときに行う対処になります📝
本日の解説は、ここまでとします
このような歴史や先行研究をしっかり理解した上で、卒業論文執筆に取り組んでいきたいです
今回、私が卒業論文執筆において取り上げる
24年ぶりの「円安是正」介入は本当にレアな経済政策
ということを再認識できたような気がします💖
私の研究テーマについて🔖
私は「為替介入の実証分析」をテーマに
卒業論文を執筆しようと考えています📝
日本経済を考えたときに、為替レートによって
貿易取引や経常収支が変化したり
株や証券、債権といった金融資産の収益率が
変化したりと日本経済と為替レートとは
切っても切れない縁があるのです💝
(円💴だけに・・・)
経済ショックによって
為替レートが変化すると
その影響は私たちの生活に大きく影響します
だからこそ、為替レートの安定性を
担保するような為替介入はマクロ経済政策に
おいても非常に重要な意義を持っていると
推測しています
決して学部生が楽して執筆できる
簡単なテーマを選択しているわけでは無いと信じています
ただ、この卒業論文をやり切ることが
私の学生生活の集大成となることは事実なので
最後までコツコツと取り組んで参ります🔥
本日の解説は、以上とします📝
今後も経済学理論集ならびに
社会課題に対する経済学的視点による説明など
有意義な内容を発信できるように
努めてまいりますので
今後とも宜しくお願いします🥺
マガジンのご紹介🔔
こちらのマガジンにて
卒業論文執筆への軌跡
エッセンシャル経済学理論集、ならびに
【国際経済学🌏】の基礎理論をまとめています
今後、さらにコンテンツを拡充できるように努めて参りますので何卒よろしくお願い申し上げます📚
最後までご愛読いただき誠に有難うございました!
あくまで、私の見解や思ったことを
まとめさせていただいてますが
その点に関しまして、ご了承ください🙏
この投稿をみてくださった方が
ほんの小さな事でも学びがあった!
考え方の引き出しが増えた!
読書から学べることが多い!
などなど、プラスの収穫があったのであれば
大変嬉しく思いますし、投稿作成の冥利に尽きます!!
お気軽にコメント、いいね「スキ」💖
そして、お差し支えなければ
フォロー&シェアをお願いしたいです👍
今後とも何卒よろしくお願いいたします!
この記事が気に入ったらサポートをしてみませんか?
