- 運営しているクリエイター
#スポーツテック
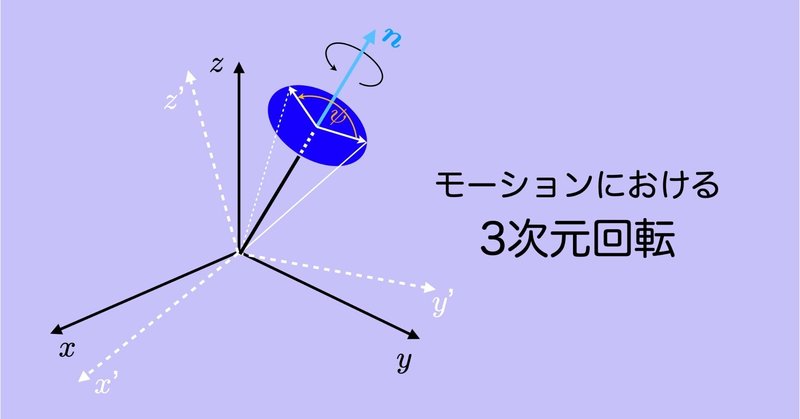
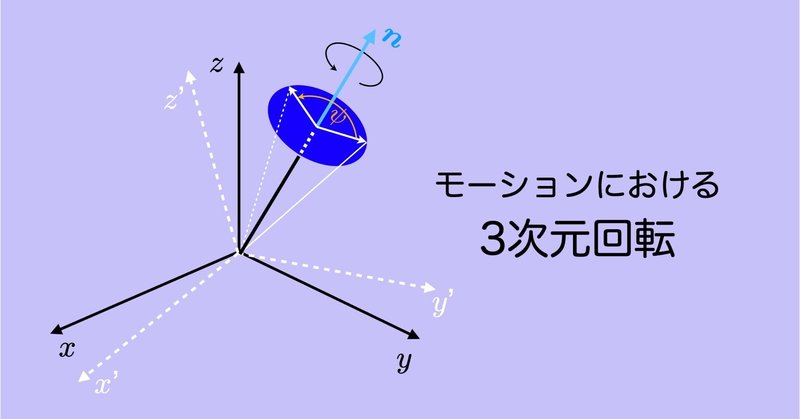
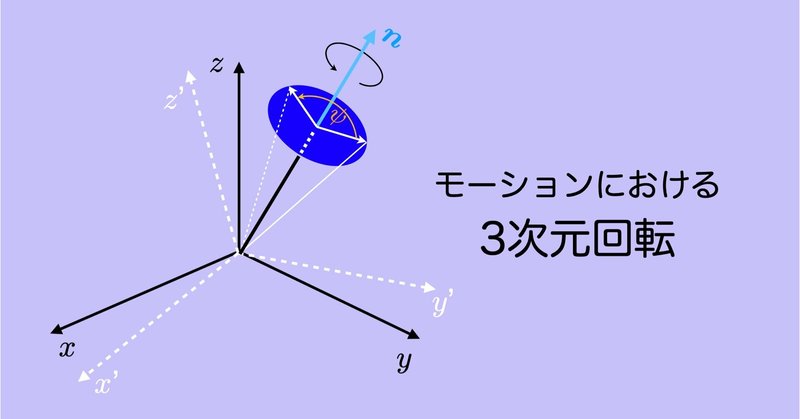
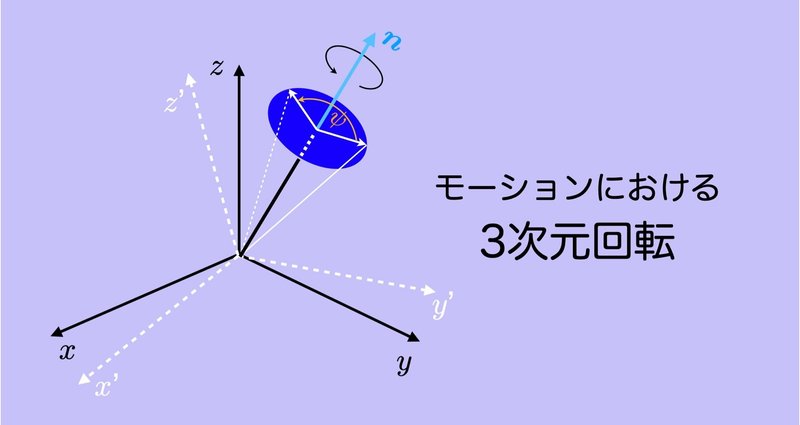
モーションにおける3次元回転 #11 〜加速度・角速度信号の座標変換〜
モーションセンサ(IMU,慣性センサ)で計測する加速度や角速度はセンサに固定されたローカル座標系の信号として計測され,モーションキャプチャは絶対座標系の位置情報を与える.また,身体運動の解析,特に力学計算では最終的には座標系を統一されて計算されるが,その計算過程ではそれらが混在するので,ローカル座標系と絶対座標系間の変換が必要となる.
これまで,回転行列をその名の通りベクトルを回転させる行列とし
モーションにおける3次元回転 #10 〜平面角度の計算〜
バイオメカニクスの解析では身体や剛体の3次元回転の解析を行うよりも,「内外転角」や「回旋角」などの1自由度の回転角を解析することのほうが多いかもしれない.この1自由度の角度は平面内で記述される角度で,例えば,直線間のなす角度は2直線が形成する平面内の角度であり,直線と平面のなす角度は直線と平面が構成する面内の角度であり,回旋角度は回旋軸に垂直な面内の角度である.このように,ここでは平面内の1軸回転
もっとみるモーションにおける3次元回転 #9 〜3次元回転・公式集〜
最近では,モーションセンサやモーションキャプチャの出力も単位クォータニオンの出力が標準になりつつあり,3次元回転を扱うには単位クォータニオンの理解が不可欠である.
そこで,ここまで述べてきた3次元回転の式を単位クォータニオンによる表現を中心に以下にまとめる.
3次元回転を理解する上でオイラー角の理解も必要ではあるが,実際の計算では,ここで述べてきた単位クォータニオンのベクトルや行列表現に慣れる
モーションにおける3次元回転 #8 〜単位クォータニオンによる回転合成〜
単位クォータニオンの演算ここでは,回転合成と前章まで議論したロドリゲスの式の,単位クォータニオン(オイラーパラメータ)による表現を示す.
回転合成の節では,行列表現によってクォータニオン同士の線形計算ができることを示すが,この行列表現を用いることでMatlab, Python(Numpy)などの行列計算を利用でき,プログラミングの記述も行いやすくなり.計測制御の観点では,行列表現によってKalm
モーションにおける3次元回転 #7 〜単位クォータニオンによる回転表現〜
単位クォータニオンクォータニオンから単位クォータニオンへ
ここであらためて定義するが,クォータニオンは
$$
\bm{q}=q_0+q_1 i+ q_2 j + q_3 k=\begin{bmatrix}
q_0\\q_1\\q_2\\q_3
\end{bmatrix}
=\begin{bmatrix}
q_0\\ \bm{v}
\end{bmatrix}
$$
のように,実数で記述されたス
モーションにおける3次元回転 #6 〜クォータニオンの導入〜
単位クォータニオンとオイラーパラメータクォータニオン(quaternion)は四元数(しげんすう)とも呼ばれ,アイルランドの数学者ハミルトンが1843年に,現在ウィリアム・ローアン・ハミルトン橋と呼ばれている橋を歩いているときに,ひらめき,そのアイデア(下記の式)を橋にナイフで刻んだと伝えられている.
なお,回転を含めた2次元平面の幾何学を記述する複素数が,4次元へ拡張されたのものがクォータニオ
モーションにおける3次元回転 #5 〜ロドリゲスの式の幾何学的意味〜
前章「モーションにおける3次元回転 #4 」で,3次元回転を表すロドリゲスの式について述べたが,これは2次元平面の回転を複素数で表すオイラーの公式から単位クォータニオンへの橋渡しと位置づけていたが,もう少し補足する.
復習
図1のように,複素平面で虚数$${i}$$をかけることは,複素平面上の原点まわりの回転を意味する.
例えば,図1の実数軸上の一番右の点である$${1}$$に「虚数 $${i
モーションにおける3次元回転 #4 〜オイラーの公式からロドリゲスの式へ〜
前章「モーションにおける3次元回転 #3 」では,オイラーの公式を用いて2次元平面内の回転について説明した.
2次元と比べて3次元の回転運動の表現方法はかなり複雑である.この章では,3次元の回転行列のもう一つの表現方法である,ロドリゲスの式について説明する.クォータニオンはロドリゲスの式と密接に関係することから,ここでの目的は,これを学ぶことによって,次章(モーションにおける3次元回転 #5 )で述
モーションにおける3次元回転 #3 〜複素数による2次元平面の回転〜
複雑な3次元の回転について説明する前に,複素数を利用した平面内の回転運動について説明する.クォータニオンとは,この複素数を利用した回転表現の3次元空間への拡張であるので,この理解を避けてとおることはできないし,この理解が3次元空間の回転をより深く理解することにつながるはずである.
複素数とオイラーの公式複素数と回転が関係すると言っても,なかなかピンとこないかもしれないが,ここでは,まず,一直線を
モーションにおける3次元回転 #2 〜方向余弦行列としての回転行列〜
前章「モーションにおける3次元回転 #1 」で方向余弦行列について触れたが,モーションキャプチャで回転行列を計算する際,多くの場合,方向余弦行列を算出することになるため,ここで少し方向余弦について補足しておく.
前章では,正規直交基底とは直交する座標系の各軸に固定された3つの単位ベクトルで,回転行列はこの正規直交基底を並べたものであることを述べた(図1).
図1の場合,直交する座標系の各$${X
モーションにおける3次元回転 #1
はじめに
バイオメカニクスの解析では,たとえば「腕と地面のなす角度」「腕の回旋角度」を算出するなど多種多様な解析が必要とされ,問題に応じて自分で解析方法を考えなくてはいけないことが多い.
また,モーションキャプチャなどで関節点の3次元位置が得られているなら,比較的これらの計算は容易であるが,モーションセンサ(IMU)でクォータニオンが出力され,そこからセンサの傾き角度をどのように算出するかとな