
モーションにおける3次元回転 #1
はじめに
バイオメカニクスの解析では,たとえば「腕と地面のなす角度」「腕の回旋角度」を算出するなど多種多様な解析が必要とされ,問題に応じて自分で解析方法を考えなくてはいけないことが多い.
また,モーションキャプチャなどで関節点の3次元位置が得られているなら,比較的これらの計算は容易であるが,モーションセンサ(IMU)でクォータニオンが出力され,そこからセンサの傾き角度をどのように算出するかとなると,少し悩むことがあるかもしれない.このように,平面内の回転と異なり3次元空間における回転に関する解析はややハードルが高くなる.
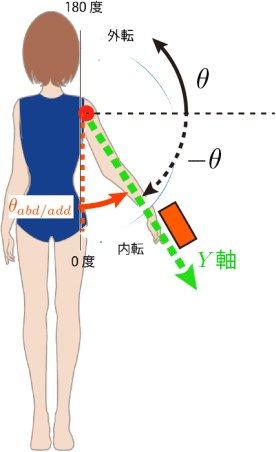
恐らく,このようなすべての角度を計算するツールや公式を作ることは難しいだろう.モーションセンサを用いて計算する際と,モーションキャプチャを用いて計算する際では,解析方法は大きく異る.そこで,ここでは3次元空間における回転運動の計測・解析を行う上での注意点をまとめ,自力で問題解決する力を養うことを目指していく.このため,数学の教科書のように数学的な証明ではなく,できるだけ回転の数理の意味を直感的に捉えることに注力し,その幾何学的理解や,実際の解析と数学との間の行間を埋めることを心がけて今後のトピックを取り上げる.
3次元空間における回転
回転運動を記述する線形変換はよく知られた回転行列である.ロボティクスの教科書では以下のような導入はほとんどないが,多くのバイオメカニクスの教科書や一部のコンピュータグラフィックスの教科書における回転行列の導入では,2次元の回転(ここでは角度$${\theta}$$の平面内の回転)
$${\bm{R}(\theta) = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta &\cos \theta \end{bmatrix}}$$
を取り上げ,このように1つの軸回りの角度$${\theta}$$による回転によって記述できることから,その延長で3次元回転も,
$${\bm{R}(\alpha, \beta, \gamma) = \begin{bmatrix} 1 & 0 & 0\\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha &\cos \alpha \end{bmatrix} \begin{bmatrix} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0\\ -\sin \beta & 0 & \cos \beta \end{bmatrix} \begin{bmatrix} \cos \gamma & -\sin \gamma & 0\\ \sin \gamma &\cos \gamma & 0\\ 0 & 0 & 1\end{bmatrix}}$$
のように3つの軸回りの回転の積で記述することで,3次元の回転を導入することが多いように見受けられる.
直交行列
しかし,回転の幾何学的な本質は1つの軸で幾何学的に表現できるにも関わらず,この導入の仕方ではわざわざ3つの軸回転を持ち出し,結果どのような回転運動を実現しているか直感的にはわからず,回転の数学的な本質を捉えにくい.そこで,ここでは,回転行列が直交行列(orthogonal rotation)であるという本来の性質に絞って説明をしていく.
物理学における物体の3次元空間における回転は,その物体のすべての点間の距離関係が変化しない線形変換を指している.ここで線形変換は,とりあえず
$${\begin{bmatrix} a & b & c\\ d & e & f \\ g &h &q \end{bmatrix} }$$
のように,要素が1次(2乗や3乗でもなく,積で表現されることもない数)の3x3の行列で表されると理解してほしい.剛体(rigid body)とは,まさに距離と方向の不変関係を保った粒子の集合なので,剛体の運動の記述においても,3次元空間における回転は剛体の運動の基本となる.
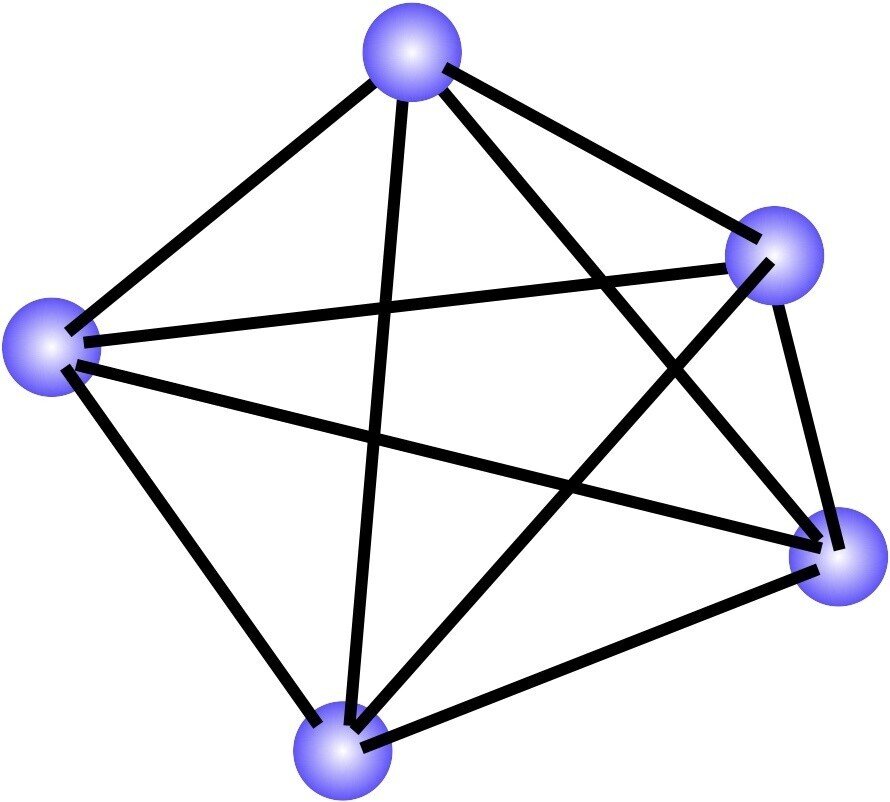
ただし,距離関係は変わらずとも鏡映(たとえば右手系と左手系のような対称な関係)とはならない変換である.なお,鏡映関係となる線形変換の行列式は-1となり,回転行列の行列式は1となり区別できるが,ここでは行列式については深く立ち入らない.
なお,中には「回転行列を三角関数で表現しないといけない」と刷り込まれている人がいるかも知れないが,3次元回転では,それはむしろ望ましくない回転表現方法と考えたほうが良い.ロボットの関節のアクチュエータが直交する3軸で構成されているなら別であるし,もちろんそれは間違いではないのだが,少なくとも回転を数学的に理解する上でも,解析する上でも,使用しないで済むならできるだけ三角関数で回転を表現することを避けたほうが望ましいと考えたほうが良いだろう.それは,後々理解できるはずである.
回転行列は直交行列である
回転を数学的に適切に表現するために,最初に述べた「点間の長さ関係を保つ線形変換」の定義に立ち返る.ここでは,詳細な線形変換の説明はとりあえず線形代数の教科書にゆずり,とりあえず,回転の線形変換は3次元の場合3x3の行列$${\bm{R}}$$で表されるとしておく.
そこで,上記の性質を満たす線形変換は,任意のベクトル$${\bm{a}}$$に対して,
$${||\bm{Ra}||=||\bm{a}||}$$
と書くことができる,つまり,ベクトルの大きさ(ノルム)の関数を$${||・||}$$で表すと,任意のベクトル$${\bm{a}}$$の長さ(大きさ)も,それに対する線形変換$${\bm{Ra}}$$のベクトルの長さも等しいことを,この式は示している.図2の各粒子間の距離をベクトル$${\bm{a}}$$の長さで表すとすると,それに対して回転$${\bm{R}}$$をほどこしても,長さは不変であることを意味している.
本来は,この関係から,そのような性質を持つ行列を導出すればよいのだが,それは教科書にゆずることとして,ここでは直感的な理解を優先して,以下のように答えを先取りする.
物理における3次元回転とは,剛体の姿勢であると言い換えることができる.なぜなら剛体が回転することで,剛体の向きを変えるからである.この剛体の向きが姿勢と呼ばれ,英語ではattitudeまたはorientationと呼ばれる.
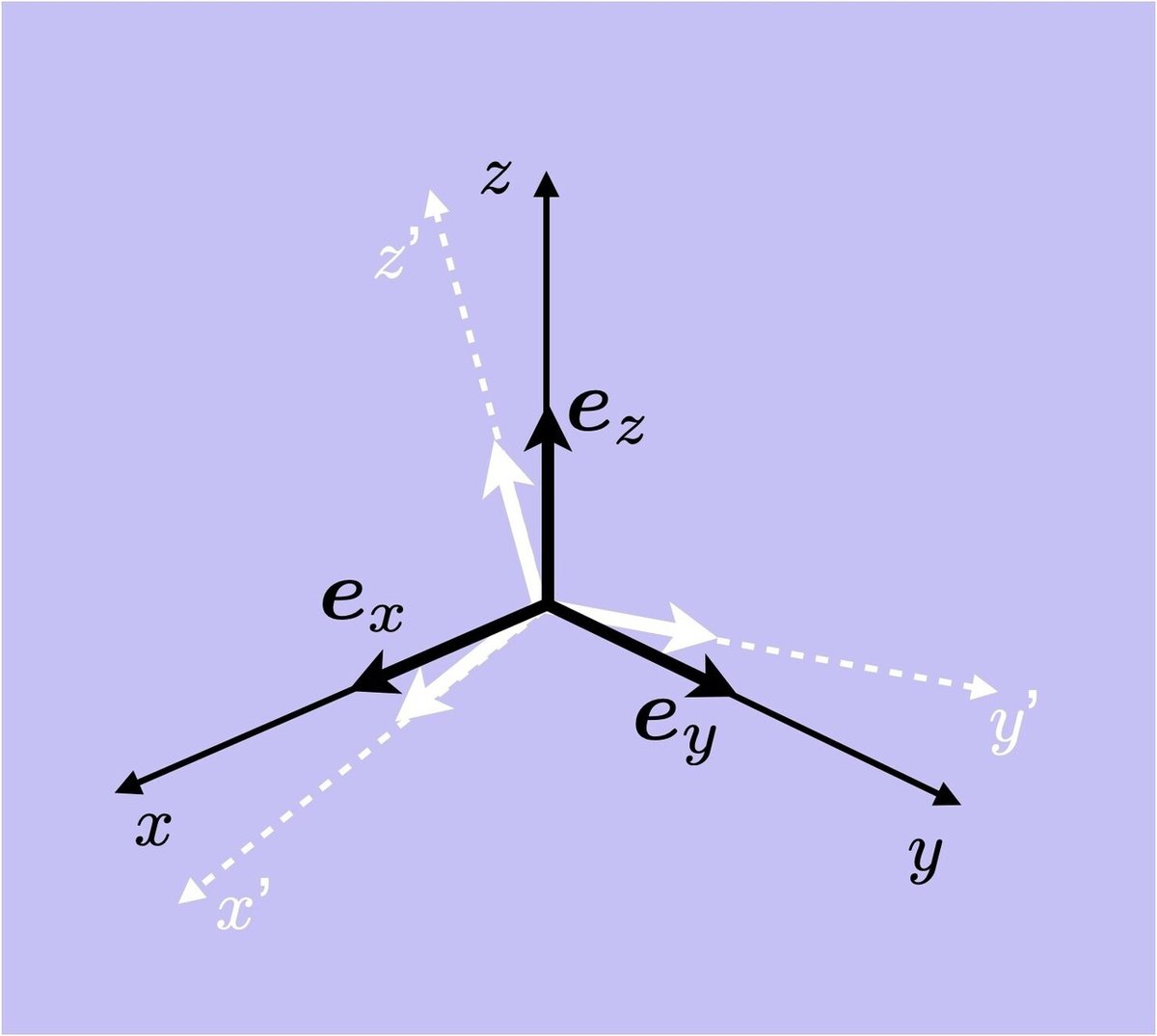
そこで,「絶対座標系から見て剛体がどちらの方向を向いているか」,すなわち剛体に固定された直交する座標系の3つの軸に単位ベクトル$${\bm{e}_x, \bm{e}_y, \bm{e}_z}$$を貼り付け,そのベクトルを並べた行列を作ることで姿勢を表すことにする(図3).この各々の軸に固定された単位ベクトルを基底ベクトルという.基底ベクトルを並べたもので姿勢を表すのだが,これが先に述べた回転(姿勢)を表す線形変換となっている.つまり
$${\bm{R} = [\bm{e}_x~\bm{e}_y~ \bm{e}_z]}$$
が回転行列である.なお,単位ベクトルの大きさは1で正規化され,それぞれの単位ベクトルは直交しているので,このような基底は正規直交基底と呼ばれる.つまり,回転ベクトルを構成する要素は正規直交基底である.
なお,一部の読者は「正規直交基底を並べたこの線形変換は姿勢を表してはいるが,回転を表してはいないのでは?」のような疑問をいだく方もいらっしゃるかもしれない.しかし,具体的に回転行列の9成分を計算する際には,例えば「絶対座標系から見た」各基底ベクトル$${\bm{e}_x, \bm{e}_y, \bm{e}_z}$$の成分を並べることになるので,$${\bm{R}}$$は単にそれらの方向を示しているだけでなく,「絶対座標系に対する」方向を示している.つまり正規直交基底,すなわち回転行列は,単に物体(剛体)の「姿勢」や「方向」を示すだけではなく,「絶対座標系と物体に固定された座標軸間の回転」を示している.もちろん,絶対座標形から見た姿勢間の関係ばかりではなく,任意の座標系間の回転も同様に表現ができる.
なお,この正規直交基底は絶対座標系からみた方向余弦に相当するので,回転行列は方向余弦行列と呼ぶこともある.なお,方向余弦行列については,次の章で詳しく説明していくことにする.
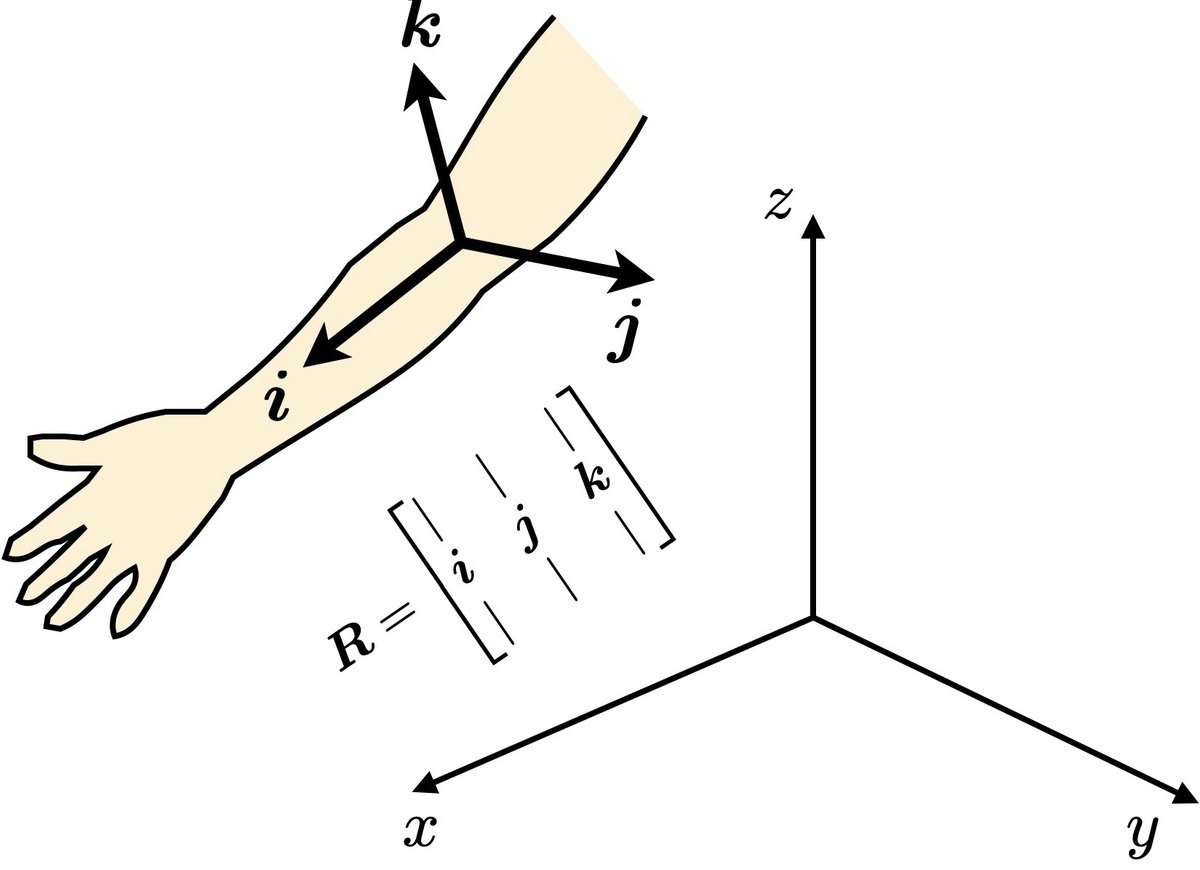
また,ここでは証明しないが,もちろん,このとき,線形変換$${\bm{R}}$$は任意のベクトル$${\bm{r}}$$に対して,
$${||\bm{Rr}||=||\bm{r}||}$$
を満たしている.
なお,このような性質を持つ回転行列は$${\bm{R}}$$は直交行列(orthogonal matrix)となる.つまり,回転行列は直交行列である.ただし,前述の鏡映関係となる変換も直交行列となるので,厳密には必要十分条件として「行列式が1となる直交行列」が回転行列である.
次からの章に向けて
では,実際にモーションキャプチャなどでデータを解析する際に,三角関数で回転行列を表現しないで,どのように回転行列を表せばよいかが問題となるが,その答えは単純で,まず剛体に固定した正規直交座標系を定める.すなわち最低3点のマーカが必要となるが,3個以上のマーカーから直交座標系を定めればよい.つまり剛体に固定されたx, y, z軸の方向の直交する単位ベクトルを定めて,
$${\bm{R} = [\bm{e}_x~ \bm{e}_y~ \bm{e}_z]}$$
のように並べればよいだけである(具体的な説明はどこかで述べる).
モーションセンサ(IMU)であれば,後ほど説明するクォータニオンを直接出力してくれる(最近のほとんどのIMUはクォータニオンを出力するようになった)ので,クォータニオンから回転行列を計算すれば良い(後述).ただし,運動中のIMUのクォータニオンの精度には気をつけたほうが良い.
さて,問題は三角関数で表現する場合はミニマムの回転の3自由度,すなわちオイラー角の3変数で表現できるが,残念ながら回転行列を計算する際には9個の変数が必要となる.数値計算上は9個の変数を保持してで表現することは無駄であるが,とりあえず回転の数学的・幾何学的な意味を理解する上では,こちらのほうが望ましい.また,オイラー角で物体の回転や姿勢を表すことはできても,回転にまつわる演算を行う際には,9個の変数で表現された回転行列を必ず経由して計算することになってしまう.
一方,この後で説明していくことになるクォータニオン(四元数:しげんすう,quaternion)に,さらに大きさが1という拘束を与えた特別な単位クォータニオン(オイラーパラメータとも呼ばれる)によって,回転を表現することになるが,単位クォータニオンを用いた回転と回転の積は,回転行列を経由せずとも単位クォータニオン同士の閉じた計算で積を計算することも可能とする.何よりも単位クォータニオンのほうが回転を直感的に表現できる.そこで,次に,単位クォータニオンによる回転の幾何学と数学の関係について述べていく.なお,オイラー角による姿勢表現については理解すべきであるが,少なくともバイオメカニクスなどの解析の計算で使用することが避けられるなら,単位クォータニオンまたは回転行列のまま回転について計算するほうが精度などを考えても無難である.
数学の教科書なら,次に直交行列の性質(回転行列と直交行列の違いは行列式だけなので)を数学的に説明することで回転を説明するのが本来であるがそれは少し後回しにし,回転の理解を深めるために,複素数を使用した3次元の回転の表現方法について次に述べていくことにする.なお,この複素数による回転表現は,解析を行う上ではあまり利点はないかもしれない.ここでは,回転を一つの軸と一つの回転角度で表す直感的な方法を導入するための,すなわちクォータニオンを理解するための入り口として複素数による説明を試みる.少し遠回りであるが,恐らく解析で有用なクォータニオンや直交行列を直感的に理解する上では,このような遠回りが必要となる.
参考文献
1.3次元回転ーパラメータ計算とリー代数による最適化ー,金谷健一著,共立出版
2.ロボットモーション(岩波講座ロボット学2),内山勝・中村仁彦著,岩波出版
なお,2はすでに絶版であるが,回転の運動学のみならず,回転の力学を理解する上でも良書である.


【解析・受託開発について】
スポーツセンシングでは、豊富な知見を持つ、研究者や各種エンジニアが研究・開発のお手伝いをしております。研究・開発でお困りの方は、ぜひスポーツセンシングにご相談ください。
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他、幅広い分野をカバーしておりますので、まずはお気軽にお問い合わせください。
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
