マガジンのカバー画像

数学月間

602
本
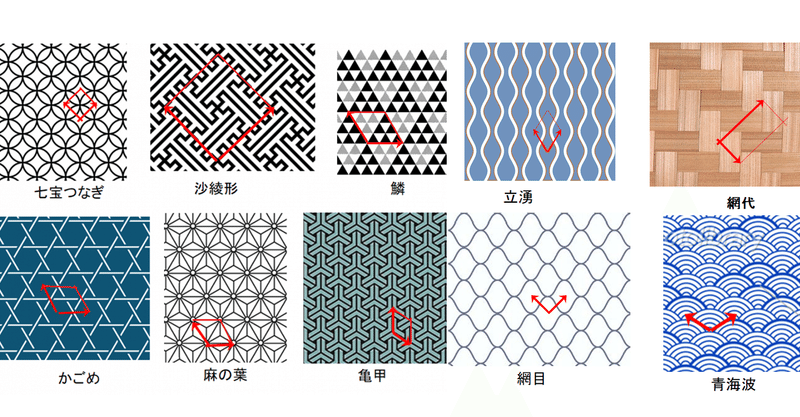
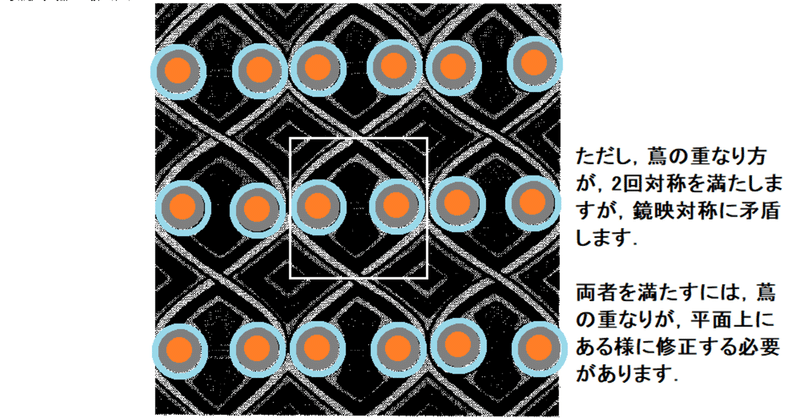
社会と数学の架け橋＝数学月間(7月22日--8月22日)．この期間は，π(22/7=3.142..) とe(22/8=2.7..) に因んでいます．この期間に，数学への関心を高め…
運営しているクリエイター
sgk
sgk

sgk

セシウム：事実と数字１（高効率太陽電池）

セシウム：事実と数字１（高効率太陽電池）

https://elementy.ru/nauchno-populyarnaya_biblioteka/435688/Tseziy_fakty_i_faktiki

A.Motylyaev 「ChemistryandLife」 No。11、2020

1860年、シュヴァルツシルトのミネラルウォーターサンプルの発光スペクトルを研究していたロバート・ブンセンとグスタフ・キルヒホフは、その中に明るい青

もっとみる
sgk

sgk

「未知」の肖像。レオナルド・オイラー300周年へ（下）

「未知」の肖像。レオナルド・オイラー300周年へ（下）

Академик Георгий Сергеевич Голицын　ゴリツィン
«Природа» No6, 2007
https://elementy.ru/nauchno-populyarnaya_biblioteka/430479/Portret_neizvestnogo_K_300_letiyu_Leonarda_Eylera

ハンドマンと私のオイラーの肖像画を見ると、オイラーは明らか

もっとみる
sgk

sgk

「未知」の肖像。レオナルド・オイラー300周年へ(上)

「未知」の肖像。レオナルド・オイラー300周年へ(上)

Академик Георгий Сергеевич Голицын　ゴリツィン
«Природа» No6, 2007
https://elementy.ru/nauchno-populyarnaya_biblioteka/430479/Portret_neizvestnogo_K_300_letiyu_Leonarda_Eylera

レオナルド・オイラーは18世紀の偉大な科学者です。その前世

もっとみる
sgk

sgk

繰り返し模様のまとめ

繰り返し模様のまとめ

17種類の平面群の対称要素のマップとパターンを一覧にまとめます．

■17種類の平面群の対称要素のマップ

■17種類の平面群の非対称モチーフのパターン

sgk

sgk

オイラー学派のソボレフ２

オイラー学派のソボレフ２

ソボレフと原子爆弾
人間の力は、理想的な無形の価値を創造し伝達する能力にあります。数学は、無謬の知的技術の最古の技術を保持しています。根拠のある計算の科学と芸術、数学は文化の中心に位置しています。思想の自由は、個人の自由の必須条件です。世界観の基礎である数学は、自由の基礎となり保証人となります。オイラーとそのスクールの最高の代表者の仕事は、これの無数の例を提供しています。ソボレフの運命も例外ではな

もっとみる
sgk

sgk

繰り返し模様p6とp6mm

繰り返し模様p6とp6mm

■第16のクラスは国際記号でp6，ロシア式記号で(a/a):6です．
表紙のエッシャーの作品は．この対称性です．トカゲの色は区別できないとすると，トカゲの左手が６つ集まっている点に6回軸があることを見出します．

以下のペルシャのパターン（Owen Jones）の例では，黒い6角形の内の花は厳密には6回対称ではありませんが，これを6回対称とみなすと，周りに風車がまわっているような6回軸の配列のパタ

もっとみる
sgk

sgk

繰り返し模様p3m1とp31m

繰り返し模様p3m1とp31m

■第14のクラスは，国際記号でp3m1，ロシア式記号で(a/a):m･3と記述します．対称性3･mの図形を60°で交差する等価な２つの軸(a/a)に沿って並進させて得られますが，鏡映面（赤色）の入り方が，並進軸（青色）に直交している．

非対称要素（黄色）が6個で単位胞を埋める．

■第15のクラスは，国際記号でp31m，ロシア式記号で(a/a)･m･3と記述します．並進の格子は(a/a)で同じで

もっとみる
sgk

sgk

オイラー学派のソボレフ１

オイラー学派のソボレフ１

［訳者注］量子力学の数学的基礎(ノイマン）がベルリンで出版されたのは1932年，みすずから日本語訳の出版がされたのは1957年です．ソボレフ達がスミルノフ主催のセミナーで勉強したのはこの本でした．ディラックのデルタ関数を厳密に扱うにはルベーク積分やヒルベルト空間の理論を基礎に置くことが必要でした．ソボレフの名はソボレフ空間に残っています．
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

もっとみる
sgk

sgk

繰り返し模様p3

繰り返し模様p3

壁紙模様の対称性の第13番目のクラスは，対称性3の図形を，60°で交差する２つの等価な並進軸(a/a)で並進して得られる．

国際記号でp3，ロシア式記号で(a/a):3です．今回から始まる残り５つの対称性のクラス（第13~17）は，正3角形のメッシュに属します．

等価な図形が隙間なく平面を充填しているこの対称性のパターンを以下に示します．モチーフ（非対称要素）は，正3角形メッシュ座標を作ってい

もっとみる
sgk

sgk

繰り返し模様p4gm

繰り返し模様p4gm

対称性の第11クラスです．国際記号p4gm，ロシア式記号(a:a):4･~a

このパターンは，4回対称の単位胞を，２つの等価な互いに直交する映進面で繰り返し広げて得られる．
縦，横の映進面~aは，群4･mに同型な，法による点群4･~aの4回軸を通る．

上の図はこの対称性のエジプトのパターンです．

縦，横の太い赤線は鏡映面．細い赤線は映進面．映進面の交点に4回回転軸がある．太い線の交点には2回

もっとみる
sgk

sgk

繰り返し模様p4mm

繰り返し模様p4mm

繰り返し模様の対称性の第12のクラスは，4･mの図形を正方形単純格子(a:a)で並進させて得られる．

この対称性は，交際記号でp4mm，ロシア式記号で（a:a):4･mと記述する．
この対称性のパターンの例は

基本モチーフタイル（非対称要素）は，単位胞の1/8です．

この対称性の日本の伝統模様はたくさんあります．
例えば，以下の七宝つなぎなどです．

イスラムの模様との交流もあったと思われま

もっとみる
sgk

sgk

繰り返し模様p4

繰り返し模様p4

繰り返し模様の対称性の第10のクラスは，国際記号でp4，ロシア式記号で(a:a):4です．単位胞の図形の対称性4を，直交する軸（従って，正方形のメッシュが格子）に沿って並進して得られるパターンである．(a:a):4で記述される．以下の２つのエジプト模様の例は，ちょっと見るとこの対称性のようですが，厳密には，この対称性を満たしません．

問　どこがいけないのか間違い探しをしましょう．

解答

上の

もっとみる
sgk

sgk

繰り返し模様pmm2

繰り返し模様pmm2

今回は，壁紙模様の第９のクラスです．国際記号でpmm2，ロシア式記号で（b:a):2･mです．

対称性2･mの単位胞図形を長方形の格子a軸，b軸で並進してパターンができます．
以下の図は，この対称性のパターンとはわずかに違うのですが，どこが違うかわかりますか？間違い個所を見つけてください．

例えば，ダイアモンドを頂点とする長方形が単位胞ですが，この単位胞の中身の対称性は，どうでしょうか．中心に

もっとみる
sgk

sgk

繰り返し模様cmm2

繰り返し模様cmm2

17種類の壁紙模様の対称性の第８クラスは，
国際記号でcmm2，ロシア式記号で(a/a):2･m　です．

点群2･mの図形を，並進の大きさは等しいが対称面(赤線)には斜交する軸（青線）(a/a)に沿って並進させて得られるので，(a/a):2･mと記述できる．
あるいは，面心格子c［黒いダイヤに注目すると面心格子が見えてきます］で，同じ点群2･mの図形を並進させると得られる．
菱形格子［単純格子］

もっとみる