
数学 | 直観的に「中間値の定理」「平均値の定理」を把握してみよう!🌠
数式はとりあえず無視してよい
数学が嫌いな人にとって、数式はできれば見たくないもの、避けられるなら極力避けたいものである。
私は学生時代、経済学部だったが、数学は必修科目ではなかった。最先端の数理経済学では、高度な数学を扱うが、ベイシックな経済学の理論を学ぶには、高校生までに学ぶ「微積分」の基礎的な知識があれば十分だと思う。
しかし、高校生までに学ぶ数学もかなり難しい。特に文系出身の者にとっては(私も文系でしたけど😄)。
そこで、今回の記事では、微積分で学ぶ「中間値の定理」と「平均値の定理」を極力数式を用いないで、説明してみたいと思う。
「当たり前じゃん!」と思うかもしれないが、当たり前だからこそ、汎用性がある。
もちろん、数学の記事なので、一応、教科書的な数式による説明も書いておくが、読み飛ばしても大丈夫💝。

中間値の定理とは?
教科書では、「中間値の定理」は次のように説明されている。
f(x)を閉区間 [ a, b ]で定義された連続関数とし、Dを
f(a)<D<f(b)
となる実数とするとき
D = f(c), (a<c<b)
を満たす実数 c が存在する。
これを中間値の定理(intermediate value theorem)という。
なんのこっちゃ?!、と思っても無理もない。耳で聞いただけで理解できる人はどれだけいるだろう?
「中間値の定理」の具体的イメージ
まず、「閉区間」とは、簡単に言えば、始まりと終わりがあるということ。そして、「連続関数」とは、途中が切れていない繋がった「曲線」(あるいは直線)であるということ。
少し具体的にグラフをかいてみる。

例えば、何でもいいのだが、
(2, 1)という座標の点Aと
(4, 4)という座標の点Bがある。
X軸(横線)の、2から4の間に、点Aと点Bを通る線を適当にかいてみよう。
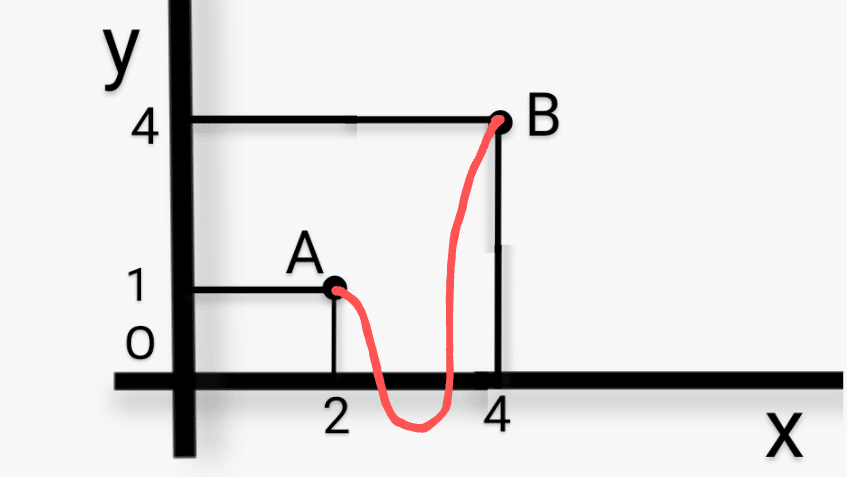

赤い曲線も青い曲線もテキトウにかいたものだが、いずれにしても、Xの値の範囲が2から4までならば、それに対応するYの値には、必ず1から4までの値が含まれていることが分かるだろう。
これが「中間値の定理」の意味することである。

平均値の定理とは?
「平均値の定理」の教科書的な説明は次の通り。
関数 f(x)が、閉区間 [a, b]で連続、
開区間(a, b)で微分可能であるとき
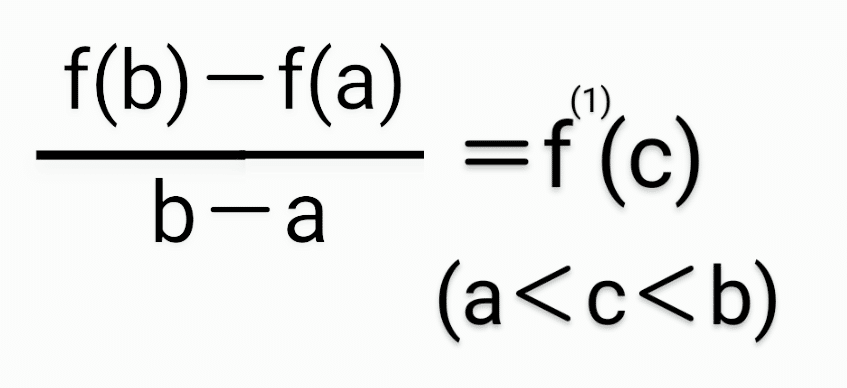
なる点Cが必ず存在する。
これを平均値の定理
(mean value theorem)という。

図4の数式の左辺は、中学生で学ぶ一次関数や二次関数でも学んだ「変化の割合」と同じである。
変化の割合とは、
(yの増加量)÷(xの増加量)のこと。
2つの点を結んでできる直線の「傾き」のことである。
「平均値の定理」を図で理解してみよう。
たとえば、下のような関数(曲線)がある。そして、その曲線に
任意の異なる点Aと点Bをとる。

そして、点Aと点Bを直線(線分)で結ぶ。
(これを「割線」という)
このとき、Xの値がaからbの区間には、必ず「割線」と同じ傾きをもつ接線がある、というのが「平均値の定理」の主張である(↓)。

平行になる「接線」が
必ず区間内にある!🌠

「平均値の定理」を使って考えてみよう!
私は今、東京にいる。広島に住む知り合いの「かわいい女の子👧🎀」に会いにいくことにした。
私はシャイなので、女の子のいる広島某所の地点の「方角」を一度も見ることなく、広島にたどり着くことはできるだろうか?

かわいい女の子👧に
会いたい💝
女の子の方角を一度も見ることなく会いに行きたい。
「平均値の定理」を使って考えてみよう。
まず、男の子👦と女の子👧のいる地点を「割線」で結ぶ。
そして、いろいろなルートを考えてみよう。

例えば「赤い線ルート」はどうだろう?

これは「割線」と平行になるとき(方角が同じ)があるから、条件を満たさない😢。
こんなルートはどうだろう?

会いにいく💝
「ぐるんぐるん🌀ルート」は、確かに、女の子👧の方角に「目線」を向けることなく行ける。しかし、「平均値の定理」の主張は、「割線」と「接線」とが、必ず「平行になる地点」があるということ。なので、残念ながら「ぐるんぐるん🌀ルート」も「平均値の定理」の呪縛から逃れられたわけではない。
まとめ
今回は久しぶりに「数学」をあつかった。理系ならば、微積分の計算や、微分方程式など用いる機会はあるかもしれない。しかし、大多数の人は、微分どころか、日常生活の中で、二次方程式を解くことも皆無だろう。だから、数学は無用だ!と主張する人もいるかもしれない。しかし、思考力というか、物事の本質をとらえるためには、数学的発想は必要不可欠だと思う。たまには、これってどういうことなのだろう?と、「数式を用いない数学」をしてみるというのは、結構楽しいものだ。
#数学がすき #算数がすき
#中間値の定理 #平均値の定理
#変化の割合 #傾き
#曲線美 #おっぱい #恋愛
#女の子 #男の子 #数学
#算数 #微分 #微乳 #積分
#巨乳 #イラスト #女
記事を読んで頂き、ありがとうございます。お気持ちにお応えられるように、つとめて参ります。今後ともよろしくお願いいたします
