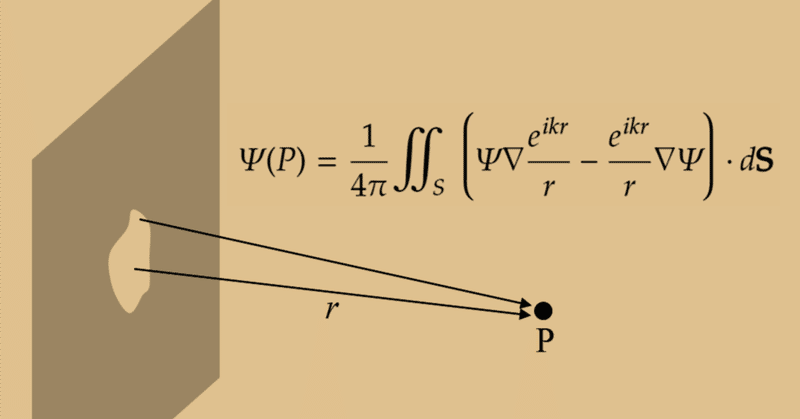
指と指の隙間に見える干渉縞の謎―意外と難しいその発生原理―
指で簡単に干渉縞を見る方法
光が波としての性質を持つ実例として、二重スリットを通した光が干渉縞を生成する現象は、高校の物理でも習う基本的な事項である。二重スリットの実験は、レーザーのようなコヒーレント光を用いれば簡単にできるのだが、太陽光や蛍光灯のような身近な光源を使う場合、干渉縞が見えるようにするには一工夫必要である(後述)。
ところが、そのような身近な光源でも、非常に簡単に干渉縞を見る方法がある。指と指でごく狭い隙間を作り、その隙間から蛍光灯等の照明を覗く。指は目の前10 cmくらいに置き、目の焦点は蛍光灯に合わせたまま、隙間を狭めて、2つの指のボケた縁を重ねると、そこに非常に細かい明暗の縞模様が現れる!何とかデジカメで撮影したのが下の写真。

指の手前に目の代わりにデジカメを置いて何とか撮影。目視ではもっと鮮明に見える。わざわざ撮影した例は珍しいかも。
さて、問題は、この縞模様の発生原理である。ネットで検索すると、「単スリットの回折」で説明している記事が散見され、自分も最近までそう思っていたが、よく考えてみるとそう単純ではない。自分が考え直して理解したところでは、これは「半無限平面による回折」である。いずれも光の干渉であることには相違ないが、隙間の幅と縞模様の周期の関係など、基本的性質が異なる。自分の理解の整理も兼ねて、あまり数式を使わず、高校レベルの平易な理解の仕方の延長で、この現象の解説を以下に試みる。
本記事の英語版はこちら↓
回折の基本
回折とは?
回折とはその字の如く、波の進路が折れ曲がって遮蔽物の裏側に回り込む現象である。電磁波では、この現象を定式化したキルヒホッフ・フレネルの回折理論というものがある。ヘルムホルツ方程式に遮蔽物の境界条件を課して導出するのだが、そこに至るまでの道のりは長い(大学の物理学科に進学して間もない頃、演習の授業でこの辺の問題が出て、難易度が一気に上がって暗然とさせられた思い出がある)。しかし、その帰結の意味するところは直観的には分かりやすい。下図のように、平面波が遮蔽板の開口部に入射すると、下流側から見た開口部は、あたかも点光源の集合のように見え、各点光源から位相の揃った球面波が出てくることになる。これを表現したのが、キルヒホッフの積分定理である。
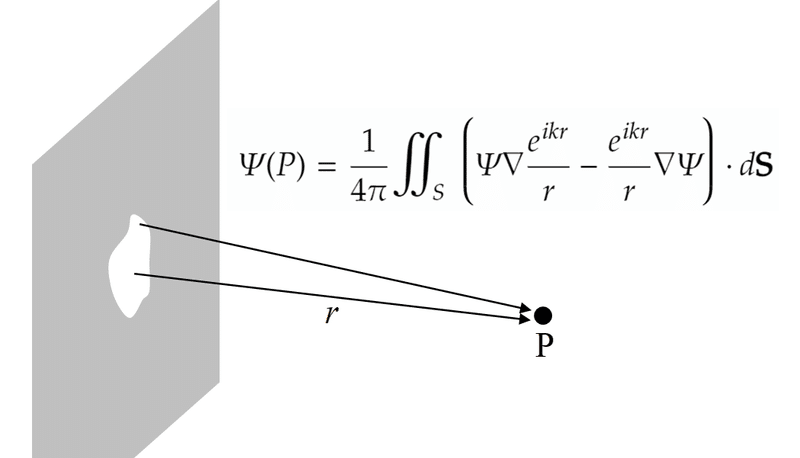
意味するところは、点Pにおける電磁場は、点Pを囲む閉曲面上の各点からの球面波の和として書ける、ということ。ホイヘンスの原理の数学的な表現に相当する。光源が遮蔽板の背後にある場合、積分に寄与するのは実質的に開口部のみである。
開口部から見て、どの方向にどれくらいの強度の光が出るかは、この積分方程式を解けば原理的に求めることができるが、下流側にあるスクリーンに投影される干渉縞の明線・暗線の位置のみ知りたい場合は、そんな面倒なことはせずとも、以下に見るように、高校の物理で習うような簡単な方法で求めることができる。
二重スリットの場合
高校の物理で習う有名な問題である。平行に並ぶ2つのスリットにコヒーレントな光を入射すると、スリット後方のスクリーンに干渉縞が投影される。この問題の場合、スリット開口部の幅は十分に狭いものとして、2つの点光源(というか「線」光源)が並んでいるとみなしてよい。

光の波長をλ、スリット間隔を$${D}$$とすると、スリットからの出射角$${\theta}$$方向に出る2つの光の光路差は、$${D\sin\theta\simeq D\theta}$$となる。これが波長λの整数倍のとき、2つの光は同位相で重なるため強め合い、波長の(整数+1/2)倍のとき、2つの光は逆位相で重なるため、強度ゼロとなる。従って、$${n = 0, 1, 2, …}$$として、
$${\theta_n = n\lambda/D}$$の方向で明線
$${\theta_n = (n+1/2)\lambda/D}$$の方向で暗線
となる。干渉縞の周期は $${\lambda/D}$$ となる。スリット間隔$${D}$$が狭いほど、それに反比例して縞模様の間隔が広がるのがポイント。
単スリットの場合
次に、スリットが1つしかない場合を考える。この場合、スリット開口部の幅そのものが問題となる。二重スリットの場合と異なり、「線光源」がスリット開口部に稠密に並んでいると見なして、それらすべての光源から来る光の重なりを考えることになる。一見複雑だが、よーく考えると、二重スリットの場合と同じ解法が使える(実際、受験生時代、難問ばかり集めた物理の参考書で、どこかの大学で出題された単スリット回折による干渉縞の位置を求める問題を見たことがある)。
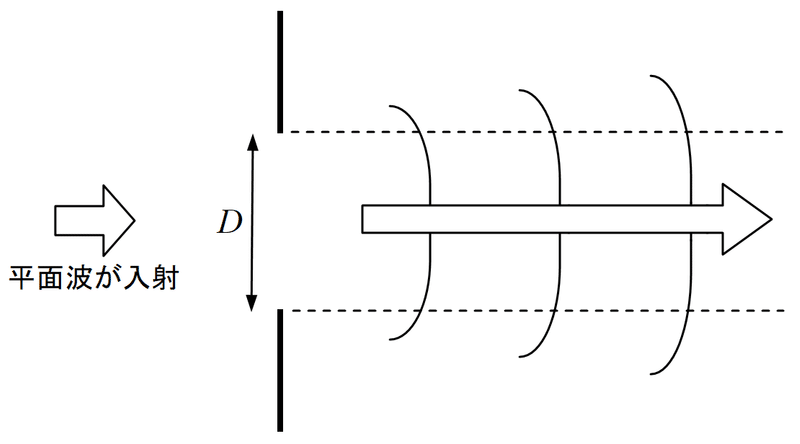
この問題は、以下のように暗線になる条件を考えると理解しやすい。スリット幅を$${D}$$とする。$${\theta=0}$$の位置では明らかに明線になる。$${\theta}$$が少しずつ大きくなると、位相がずれた光も重なってくるので強度は弱くなるが、最初に暗線となるのは、$${\theta}$$がどのような角度のときか?それは、下図のように、$${(D/2)\theta=(1/2)\lambda}$$となるときである。
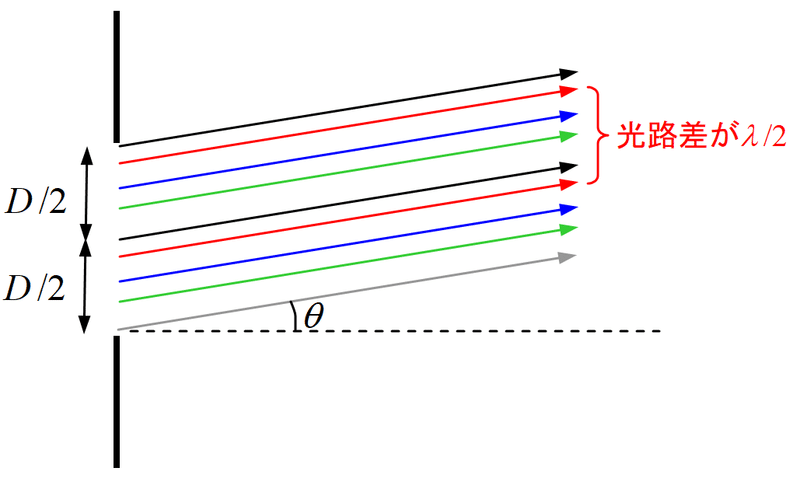
同じ色の光線のペアはすべて光路差が半波長となるため、全ての光線が打ち消しあう。
なぜならば、この条件のとき、
開口部において距離$${D/2}$$だけ離れた位置から出た2つの光は逆位相のため、打ち消し合う
任意の位置に入射した光に対して、それに対応して、距離$${D/2}$$だけ離れた位置に入射する光が必ず存在する
が成り立つため、結局、すべての光が打ち消し合うのである。同様にして$${\theta}$$を大きくしていくと、
$${(D/2)\theta=(n+1/2)\lambda}$$, $${n = 0, 1, 2, …}$$
のときに暗線となる。また、図5において、開口部を2分割ではなく4分割して考えても同じように打ち消しあうので、
$${(D/4)\theta=(n+1/2)\lambda}$$, $${n = 0, 1, 2, …}$$
のときも暗線である。同様に、8分割、16分割・・・としても同じことが言える。結局、$${n = 1, 2, …}$$として、
$${\theta_n = n\lambda/D}$$の方向で暗線(上記の条件をまとめるとこうなる)
$${\theta_0=0}$$および$${\theta_n = (n+1/2)\lambda/D}$$の方向で明線(明線は暗線の中間に来る)
となる。干渉縞の周期は $${\lambda/D}$$ であるが、$${\theta_0=0}$$の明線のみ幅が2倍になる。スリット幅$${D}$$が狭いほど、それに反比例して縞模様の間隔が広がるのは、二重スリットの場合と同じである。
観測される干渉縞の強度分布
上記の論法で議論できるのは、明線と暗線の位置のみで、観測される干渉縞の強度分布を求めるには、上記のキルヒホッフの積分定理に立ち戻る必要がある。現実的な条件を想定すると精度の良い近似解を求めることができて、結果的に、下図のようになる。単スリットの場合、ゼロ次の明線が特に大きくなるため、縞模様は実際には見えにくい。
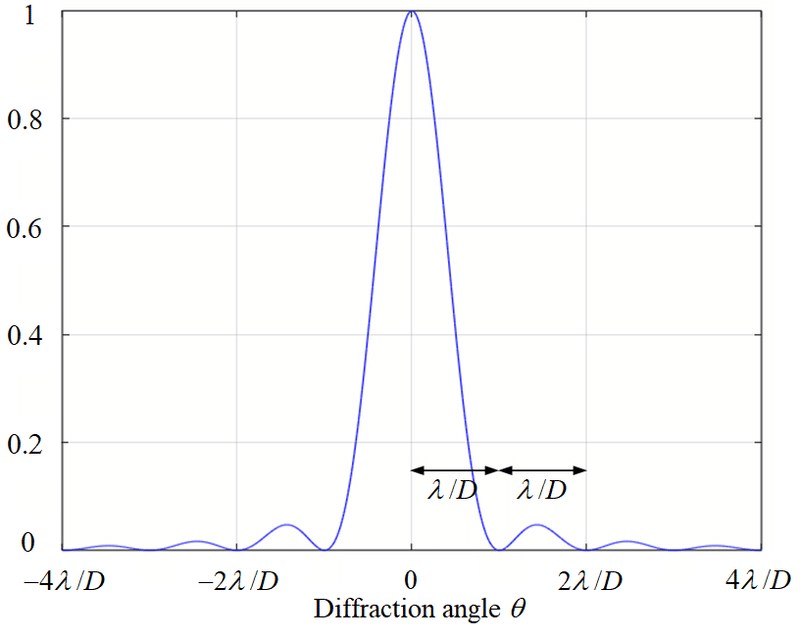
二重スリットの場合、二重スリットは2つの単スリットの組合せのため、単スリットの大きな干渉縞に、二重スリットの細かい干渉縞が重畳する(スリット間隔よりもスリット幅の方が小さいため、単スリットの干渉縞の方が周期は大きくなる)。スリット幅$${D}$$, スリット間隔$${d=2D}$$の場合の強度分布を下図に示す。単スリット回折よりも、縞模様は観察しやすい。

d = 2Dの場合。スリット単一の単スリット回折の強度分布(青点線)を包絡線として、それよりも細かい周期で干渉縞が現れる。
指の隙間に見える干渉縞は何か?
単スリット回折で説明可能?
さて、本題の指の隙間の干渉縞の問題に戻る。この干渉縞の発生原理は、どのような物理によるものだろうか?指で作った隙間は1つだから、単純に考えると単スリット回折によるものと考えたくなるが、そう単純ではない。
単スリット回折の場合、その干渉縞は、図6に示したように中心の明線が著しく明るく出るはずだが、冒頭に示した指の隙間の干渉縞は、そのようにはなっていない。縞模様の出方は、隙間の位置に依らずほぼ一様である。
また、単スリット回折の場合、干渉縞の周期はスリット幅の逆数に比例する。つまり、スリット幅を狭めるほど、干渉縞の周期は広がるはずなのだが、蛍光灯を覗いているときの指の間隔を狭めても、縞の周期が変わるようには全然見えないのである。
指だと分かりにくいので、爪切りの刃の隙間から蛍光灯を覗いたときに見えた干渉縞の写真を以下に挙げる。

隙間が狭い場合

隙間を広げた場合
上記2つの写真では、爪切りの刃の隙間の幅は少なくとも1.5倍くらい異なるが、隙間に見える干渉縞のパターンは大差ない。周期はほとんど変わらず、隙間を広げると、縞模様全体が明るくなって、明暗のコントラストが低くなるように見えるだけである。
また、干渉縞の周期$${\Delta\theta=\lambda/D}$$に現実的な値を入れても、実態と合わないのである。光の波長を$${\lambda=500\,\text{nm}}$$,スリット幅を$${D=0.1\,\text{mm}}$$として、スリットの後方$${L=10\,\text{cm}}$$の距離において干渉縞を観察するとすると、距離に換算した干渉縞の周期は、
$${\Delta x=L\Delta\theta=L\lambda/D\\\quad\ \ \,=10\,\text{cm}\times500\,\text{nm}\,/\,0.1\,\text{mm}\\\quad\ \ \,=5\,\text{mm}}$$
程度となる。干渉縞を観察している目の瞳孔の直径が3 mm程度であることを考慮すると、余りにも大きすぎるだろう。
半無限平面による回折
上記の観察から、指の隙間にできる干渉縞の周期は、隙間の幅には依存せず、他の因子によって決まっているように見える。このような性質を示す回折現象があるだろうか?ボルン&ウォルフの「光学の原理」を会社の図書室から引っ張り出して見つけたのが、半無限平面による回折である。下図のように、入射する平面波を半無限長の遮蔽板で遮ったときに生じる回折である。

回折によって光は遮蔽板後方にも回り込むが、それだけでなく、何と干渉縞が生じるのである(物理学で博士号を取得した自分だが、これは知らなかった)。
上図のように、遮蔽平面から距離$${L}$$の位置にあるスクリーンに投影される光の強度分布を考える。光の波長を$${\lambda}$$,スクリーン上の座標を$${x}$$(遮蔽平面端点の正面が$${x=0}$$)すると、強度分布は下図のようになるらしい。
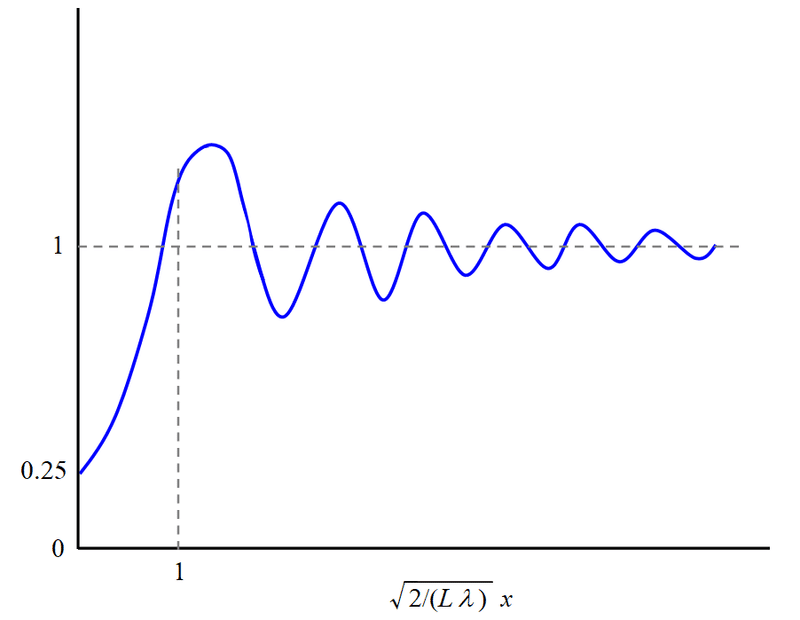
半無限平面による回折の場合、スリット幅やスリット間隔のような、長さの次元を持つ特徴量は存在しない。そのため、遮蔽版と観察位置までの距離と波長によって干渉縞の周期が決まる(この場合完全な周期関数ではないが)のが特徴である。
図11の強度分布の導出には、フレネル積分やらコルニュ螺旋やらが出てきて複雑だが(何と厳密解もあるようで、「光学の原理」の第3巻に載っている!)、図11に示したようなスケールで縞模様が現れる理由については、以下のような直観的な論法で理解可能である(ここは自分のオリジナル)。図11によると、$${x\simeq\sqrt{L\lambda/2}}$$の位置に最初のピークが現れることになるが、こうなる理由を考えよう。
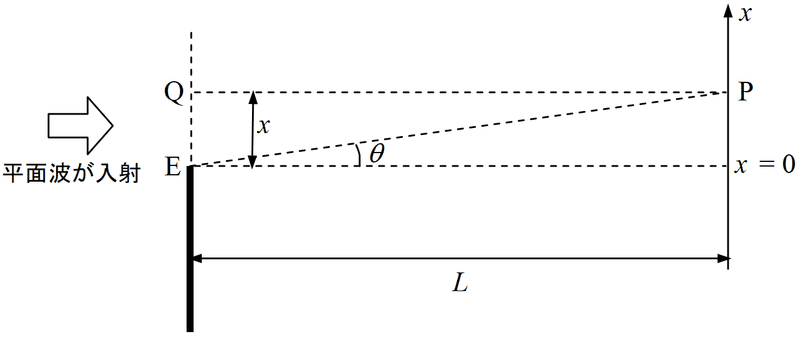
上図のように、$${x=0}$$の点近傍の点Pにおける回折光の強度を考える。遮蔽平面がない場合、点Pにおける光は、点QEを通る無限に長い直線上にある無数の点光源からの球面波の総和である。このとき、距離による減衰があるので、当然ながら、真正面の点Qからの光の寄与が最も大きい。さて、ここで、半無限の遮蔽平面を置くと、点Pに到達するはずだった球面波の半分の寄与がなくなってしまう。このとき、点Qから来る光とちょうど光路差が半波長になるような点からの光がなくなると、点Pにおける回折光の強度は、遮蔽平面設置前よりも高くなる。そのような現象が生じる最小の$${x}$$はどういう場合か?それは、EPとQPの光路差がちょうど半波長になるとき、すなわち、
$${x\theta\simeq\lambda/2}$$
が成り立つときである。$${\theta\simeq x/L}$$であるから、
$${x^2/L=\lambda/2}$$
となり、$${x\simeq\sqrt{L\lambda/2}}$$を得る。
ところで図11の強度パターン、指の隙間の干渉縞と似ているではないか!?
自分の考えでは、この半無限平面による回折こそが、指の隙間に見える干渉縞の発生原理である。そう考える根拠を以下に挙げる。
根拠1:
指で隙間を作って干渉縞を詳細に観察すると分かるが、2つの指を近づける前の段階でも、指のボケた縁をよく見ると、うっすらと縞模様が見えているのである。2つの指を近づけて隙間を狭めていくと2つのボケた縁が重なり、そのボケが重なった所に細かい縞模様が生じるのだが、このときに見えてくる縞模様は、2つの指を近づける前に元々うっすらと見えていた縞模様のコントラストが上がったように見える。この現象は、各指の縁で元々半無限平面による回折が生じていて、指の隙間を狭めると、入射する光の方向が制限されるために、結果的に光源(蛍光灯)のサイズが小さくなり、可干渉性が上がった、と解釈できる。
根拠2:
観察される一様なコントラストの縞模様と、図11の強度パターンが非常によく似ている(半無限平面による細かい縞模様は、図11に示したのより$${x}$$が大きい範囲に長く続く)。
根拠3:
干渉縞の周期も計算してみると、実測と違和感のない値が出てくる。図11を見ると、干渉縞の周期は、おおよそ$${\Delta x\simeq\sqrt{L\lambda/2}}$$程度である。上記単スリット回折の場合と同様に、光の波長を$${\lambda=500\,\text{nm}}$$,遮蔽平面と観察位置の間の距離を$${L=10\,\text{cm}}$$とすると、
$${\Delta x\simeq \sqrt{L\lambda/2}\\\quad\ \ \,=\sqrt{10\,\text{cm}\times500\,\text{nm}\,/\,2}\\\quad\ \ \,=0.15\,\text{mm}}$$
となる。目の瞳孔の直径を3 mmとして、実感に近い数値である。
干渉にコヒーレント光は必ずしも必要ではない
以上で、指の隙間に見える干渉縞は、半無限平面による回折であると結論できた。ネットで検索しても、同様の議論が見つからないため少々不安だが、大筋では合っていると思う。
ところで、この指の隙間に見える干渉縞は、レーザー等のコヒーレント光を使わずに、蛍光灯や太陽光などのコヒーレントでない光源を用いて、容易に干渉縞を作れるという特徴がある。一般に、干渉縞を作るには、光源の位相が揃ってないとダメという誤解があるが(自分も一時期誤解していた)、そうではない。例え光源の位相が揃っていなくても、光源サイズが十分に小さければ、干渉縞を作ることができる。光源サイズが大きすぎる場合、光源上の異なる点から入射する光の光路差がバラバラのため、それが効いて干渉縞が消えてしまう。それを防ぐためには、入射光の方向が揃うように適当な絞りを上流側に設置すればよい。実際、有名なヤングの実験では、二重スリットの手前に、入射光を絞るための単スリットが置かれている。この辺の事情については、以下の論文に詳しい(2023年1月現在、ネットで検索すると出てくる):
大倉宏, 2017. ヤングの実験で複スリットの手前に置かれる単スリットの役割について.大阪市立科学館報告, (27): 17-22.
指や爪切りの刃で隙間を作る場合、隙間を狭めることによって、結果的に光源サイズの極小化が達成されているわけである。
おわりに
本稿で紹介した、指の隙間て干渉縞を見る方法は、20年くらい前の大学院生のときに、日本物理学会誌の何かの記事で目にしたものである。その記事には確か単スリット回折と書いてあった気がするが、詳細な説明はなく、何となく納得していたが、それでも何となく違う気がしてモヤモヤしていた。今回、20年の時を超えて自分なりに納得できる答えに辿り着いたのは、個人的に大きな成果である。やはり、具体的に数値を理論式に当てはめて確認するのは重要である。
同じような方法で、二重スリットの干渉縞もお手軽に見る方法はあるだろうか?これは今後の課題。
この記事が気に入ったらサポートをしてみませんか?
