
第17章「抑うつを調べるための4つのツールを比較する」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング2」の第17章「抑うつを調べるための4つのツールを比較する」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
今回は心理学術的な色合いの濃いベイズ分析です。
この章は4つの抑うつ尺度を項目反応理論(IRT)で検討・比較します。
今回の PyMC 化はラッキー要素のおかげでテキストとほぼ同じ結果を得られました!
ではでは PyMCのベイズモデリングの世界を楽しんでまいりましょう!

テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 登藤直弥 先生、梅垣佑介 先生
モデル難易度: ★★★★★ (難しい)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★★★★ & GoooD! \\
結果再現度 & ★★★★★ & 最高✨ \\
楽しさ & ★★★★★ & 楽しい! \\
\end{array}
$$

評価ポイント
宿敵「Ordered」制約に勝ちました!
今回のベイズモデルは2次元変数$${\kappa}$$にOrdered制約(値の小さい順)を課します。
以前のベイズモデリングの取り組みでは2次元変数のOrdered制約を実装することができず、何度も枕を濡らしたことでしょう・・・
今回は意味があるかどうかにかかわらず PyMC 公式のサンプルコードを真似て引数を設定したところ、原理はわからないのですが行方向にOrdered制約が効いたのです!やったね!
工夫・喜び・反省
前回に引き続き、今回も「因子分析」が出現!
いつかどこかで因子分析にキチンと向き合う必要がありそうです。
今回は semopy の確認的因子分析を利用しました。

モデルの概要
テキストの調査・実験の概要
■ 分析の概要
大学生を対象にした自記式の4種の抑うつ度測定尺度の特徴を項目反応理論に基づく数理モデルを用いてベイズモデリングします。
■ データの概要
日本人大学生824名からオンライン調査で得た回答データです。
■ 分析対象の尺度の一覧
$$
\begin{array}{l:l:l:l}
尺度名 & 概要 & 得点 & 逆転項目\\
\hline
SDS & 20項目・4件法 & 1点から4点 & 10項目 \\
CES-D & 20項目・4件法 & 0点から3点 & 4項目\\
BDI-II & 21項目・4件or7件法 & 0点から3点 & なし \\
PHQ-9 & 9項目・4件法 & 0点から3点 & なし \\
\end{array}
$$
得点は、質問項目に対する回答値を変換した値です。
例えば4件法で得点が「1点から4点」の場合には、回答値が4段階あり、1点から4点に得点化しています。
BDI-IIの7件法の場合は、7段階の回答値を0点から3点の範囲で得点化するそうです。
分析の概要を図示します。

テキストのモデリング
■ 目的変数と関心のあるパラメータ
目的変数は回答者$${i}$$の項目$${j}$$の回答値$${U_{ij}}$$です。
関心のあるパラメータは抑うつ度$${\theta_i}$$、識別力母数$${a_{j}}$$、識別力母数$${\times}$$カテゴリ困難度母数$${\kappa_{jk}}$$、そしてこれらのパラメータから算出するテスト情報量、相対効率などです。
■ 数理モデル
項目反応理論に基づく数理モデルです。
回答者$${i}$$の抑うつ度が$${\theta_i}$$のとき、(質問)項目$${j}$$でカテゴリ(おそらく得点)$${k}$$と回答する確率$${P_{jk}(\theta_i)}$$が定義されます。
$$
\begin{align*}
P_{jk}(\theta_i) &= P^{+}_{jk}(\theta_i) - P^{+}_{j(k+1)}(\theta_i) \\
P^{+}_{jk}(\theta_i) &= \cfrac{1}{1 + \exp(-a_j(\theta_i - b_{jk}))} = \cfrac{1}{1 + \exp(-a_j \theta_i + \kappa_{jk})} \\
\end{align*}
$$
【変数・記号の概要】
$${P^{+}_{jk}(\theta_i)}$$は回答者$${i}$$が項目$${j}$$でカテゴリ$${k}$$以上と回答する確率
$${a_{j}}$$は識別力母数
$${\kappa_{jk}}$$は識別力母数$${\times}$$カテゴリ困難度母数
■ ベイズモデル
テキストに尤度関数の掲載がないため、Stanコードから逆引きで書きます。
$$
\begin{align*}
U_{ij} &\sim \text{OrderedLogistic}\ (a_j \theta_i,\ \kappa_{jk}) \\
\theta_i &\sim \text{Normal}\ (0,\ 1) \\
a_j &\sim \text{LogNormal}\ (0,\ 2) \\
\kappa_{jk} &\sim \text{Normal}\ (0,\ 10^2) \\
\end{align*}
$$
【変数・記号の概要】
$${U_{ij}}$$は回答者$${i}$$の項目$${j}$$の回答値です。
OrderedLogistic は順序ロジスティック分布であり、第一引数は予測子、第二引数はカットポイントです。
正規分布$${\text{Normal}}$$の第二引数は分散です。
対数正規分布$${\text{LogNormal}}$$の第二引数は標準偏差です。

■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCの自己流モデルの推論値を利用した分析は「PyMC実装」章をご覧ください。
PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.インポート
### インポート
# 数値・確率計算
import pandas as pd
import numpy as np
import pingouin as pg
# PyMC
import pymc as pm
import arviz as az
# 確認的因子分析
import semopy
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ユーティリティ
import pickle
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')2.データの読み込みと前処理
csvファイル「4scale_data.csv」をpandasのデータフレームに読み込みます。
### データの読み込み
data_orgn = pd.read_csv('4scale_data.csv')
display(data_orgn)【実行結果】
824行、70列のデータです。
行は回答者単位です。
列は尺度名と項目番号の組み合わせです。
値は各尺度・項目に対する得点(回答者の回答値)です。

データを加工します。
まずは横持ち構造から縦持ち構造に変換します。
### データ前処理:データを縦持ちに変換
## 設定
# 尺度のリスト
methods = ['SDS', 'CESD', 'BDI', 'PHQ9']
## dataを縦持ちに変換
# dataのコピー、旧indexを残す(回答者IDにする)
data = data_orgn.copy().reset_index()
# 縦持ちに変換、variableに「尺度+番号」がセットされる
data = pd.melt(data, id_vars=['index'], value_vars=data.columns)
# 「尺度+番号」から尺度を切り抜き(尺度リストから一致する尺度名を取り出してセット)
data['shaku'] = (data['variable']
.apply(lambda x: [m for m in methods if x[:3] in m][0]))
# 「尺度+番号」から番号を切り抜き(shakuにセットした尺度名を''に置換して整数型へ)
data['ban'] = (data[['variable', 'shaku']]
.apply(lambda x: int(x[0].replace(x[1], '')), axis=1))
# 列の絞り込みと列名の変更
data = data[['index', 'shaku', 'ban', 'value']]
data.columns = ['回答者ID', '尺度', '項目番号', '得点']
# データフレームの表示
display(data)【実行結果】
回答者ID別・尺度別・項目番号別の得点データの形式になりました。

続いて、尺度・回答者ID単位の合計得点データを作成します。
### データ前処理:尺度・回答者IDごとの合計得点のデータフレームの作成
data_sum = data.groupby(by=['尺度', '回答者ID'])['得点'].sum().reset_index()
display(data_sum)【実行結果】
表の見方です。
回答者ID:0の回答者によるBDI尺度の回答値の合計得点は1です。


記述統計量・確認的因子分析
テキストは重厚な分析手続きを読者に示しています。
頑張って分析手続きを進めていきたいと思います!
テキストの17.2.1項「記述統計量」、17.2.2項「尺度得点と因子間の相関係数」の分析手続きをなぞってみます。
1.記述統計量
■ 合計得点の平均値と標準偏差
尺度ごとに合計得点の平均値と標準偏差を算出します。
テキストでは188ページに文章で記載されています。
### 記述統計:各尺度の尺度得点について平均・標準偏差の算出 ※テキスト188ページ
# 尺度ごとに合計得点の平均と標準偏差を算出、methodsリスト順に行をソート
stats_df01 = (data_sum.groupby(['尺度'])['得点'].agg(['mean', 'std'])
.reindex(methods))
display(stats_df01.round(2))【実行結果】

■ 抑うつ度の分布
続いて抑うつ度の分布(人数)です。
先行研究で提案された括り(カットオフポイント)を用いています。
テキストでは188~189ページにかけて文章で記載されています。
### 記述統計:抑うつ度の分布(人数)の算出 ※テキスト188~189ページ
# CESD 閾値15
tmp = data_sum[data_sum['尺度']=='CESD']
CESDn = (tmp['得点'] <= 15).sum() # 非抑うつ
CESDp = (tmp['得点'] > 15).sum() # 抑うつ
print(f'CESD: 非抑うつ{CESDn}名, 抑うつ{CESDp}名')
# PHQ9 閾値9
tmp = data_sum[data_sum['尺度']=='PHQ9']
PHQ9n = (tmp['得点'] <= 9).sum() # 非抑うつ
PHQ9p = (tmp['得点'] > 9).sum() # 抑うつ
print(f'PHQ9: 非抑うつ{PHQ9n}名, 抑うつ{PHQ9p}名')
# SDS 閾値47, 55
tmp = data_sum[data_sum['尺度']=='SDS']
SDSl = (tmp['得点'] <= 47).sum() # 軽度/非抑うつ
SDSm = ((tmp['得点'] > 47) & (tmp['得点'] <= 55)).sum() # 中程度
SDSh = (tmp['得点'] > 55).sum() # 重度
print(f'SDS : 軽度/非抑うつ{SDSl}名, 中程度{SDSm}名, 重度{SDSh}名')
# BDI 閾値13, 19, 28
tmp = data_sum[data_sum['尺度']=='BDI']
BDIn = (tmp['得点'] <= 13).sum() # 非抑うつ
BDIl = ((tmp['得点'] > 13) & (tmp['得点'] <= 19)).sum() # 軽度
BDIm = ((tmp['得点'] > 19) & (tmp['得点'] <= 28)).sum() # 中程度
BDIh = (tmp['得点'] > 28).sum() # 重度
print(f'BDI : 非抑うつ{BDIn}名, 軽度{BDIl}名, 中程度{BDIm}名, 重度{BDIh}名')【実行結果】

■ 尺度得点の α 係数
続いて各尺度の尺度得点についての α 係数です。
クロンバックの α 係数と呼ばれる統計量です。
pingouin ライブラリの cronbach_alpha() 関数を利用します。
テキストでは189ページに文章で記載されています。
### 記述統計:各尺度の尺度得点の信頼性係数α(クロンバックのα係数)の算出
# ※テキスト189ページ, pingouinのcronbach_alpha()でクロンバックのα係数を算出
# 結果を格納するデータフレームの初期化
stats_df02 = pd.DataFrame()
# 各尺度ごとにα係数を算出してデータフレームに追加する処理を繰り返す
for method in methods:
# α係数と信頼区間の算出 pingouinのcronbach_alpha()
alpha, ci = pg.cronbach_alpha(data[data['尺度']==method],
items='項目番号', subject='回答者ID',
scores='得点', ci=0.95)
# データフレームに追加
stats_df02 = pd.concat([stats_df02,
pd.DataFrame({method: [alpha, ci[0], ci[1]]})],
axis=1)
# データフレームの縦横を変換して列名をセット
stats_df02 = stats_df02.set_axis(['α', '2.5%CI', '97.5%CI']).T
# データフレームの表示
display(stats_df02.round(2))【実行結果】
テキストによると「これらの尺度得点には十分な信頼性があると考えられた」とのこと。


2.尺度得点と因子間の相関係数
テキストは各尺度の背後に1因子(抑うつ度を表す潜在変数)を想定し、各尺度の因子の間の相関関係を想定した確認的因子分析に進みます。
■ 尺度得点間の相関係数
まずは、尺度得点間の相関係数$${r}$$を算出します。
pandas の corr() 関数で相関係数を計算します。
テキストでは189ページに文章で記載されています。
### 尺度得点間の相関係数の算出 ※テキスト189ページ
# 行:回答者ID、列:尺度、値:得点のデータフレームを作成
data_sum2 = (data_sum.pivot_table(index='回答者ID', columns='尺度', values='得点')
.reset_index(drop=True))
data_sum2.columns.name = None
# display(data_sum2)
# 尺度得点間の相関係数:corr()を算出して表示
display(data_sum2.corr().round(2))【実行結果】
テキスト記載の通り、尺度得点間には$${r=0.68-0.81}$$の強い正の相関関係が見られます。

■ 確認的因子分析・抑うつ度因子間の相関
semopy ライブラリを利用して確認的因子分析に挑みます(初挑戦)。
semopy による確認的因子分析の実装では、福中公輔様のブログを参考にさせていただきました。
ありがとうございます!
確認的因子分析を実行します。
### 確認的因子分析の実行
# semopyを利用
# 参考サイト:https://note.com/k_fukunaka/n/ncf493169157a
# 確認的因子分析モデルの定義
desc = """
PHQ9 =~ PHQ91 + PHQ92 + PHQ93 + PHQ94 + PHQ95 + PHQ96 + PHQ97 + PHQ98 \
+ PHQ99
CESD =~ CESD1 + CESD2 + CESD3 + CESD4 + CESD5 + CESD6 + CESD7 + CESD8 \
+ CESD9 + CESD10 + CESD11 + CESD12 + CESD13 + CESD14 + CESD15 \
+ CESD16 + CESD17 + CESD18 + CESD19 + CESD20
SDS =~ SDS1 + SDS2 + SDS3 + SDS4 + SDS5 + SDS6 + SDS7 + SDS8 + SDS9 \
+ SDS10 + SDS11 + SDS12 + SDS13 + SDS14 + SDS15 + SDS16 + SDS17 \
+ SDS18 + SDS19 + SDS20
BDI =~ BDI1 + BDI2 + BDI3 + BDI4 + BDI5 + BDI6 + BDI7 + BDI8 + BDI9 \
+ BDI10 + BDI11 + BDI12 + BDI13 + BDI14 + BDI15 + BDI16 + BDI17 \
+ BDI18 + BDI19 + BDI20 + BDI21
"""
# 確認的因子分析の実行
model_cfa = semopy.Model(desc)
result_cfa = model_cfa.fit(data_orgn)【実行結果】なし
確認的因子分析の「適合度」を確認します。
テキストでは189ページに文章で記載されています。
### 確認的因子分析の結果:適合度の確認 ※テキスト189ページ
# 適合度検定の結果:chi2 p-value 0.000, RMSEA 0.075
stats_df03 = semopy.calc_stats(model_cfa)
display(stats_df03.T.round(3))【実行結果】
適合度検定の p値は「chi2 p-value」の 0.000 です。1% 水準で有意です。
RMSEA は「RMSEA」の 0.075 です。テキストの 0.8 と同値と思われます。

因子間の相関関係を探ってみます。
テキストでは189ページに文章で記載されています。
算出方法をよく分かっていないので、以下のコードの適否は不明です。
また計算した相関係数はテキストと異なっています。
### 構成概念スコアの推定 ※テキスト189ページ 因子間に強い正の相関 r=0.82-0.91
# ★因子間の相関係数の算出方法がこれで良いのか不明・・・
# 因子スコアの推定の実行
factor_score = model_cfa.predict_factors(data_orgn)
# 結果表示
print('因子スコアの推定結果')
display(factor_score)
# 因子スコアの相関関係の算出
print('因子スコア間の相関関係')
display(factor_score.corr().round(3))【実行結果】
因子スコアの予測値に対して相関係数をはかってみました。

テキスト風に記述をするなら「$${r=0.90-0.97}$$」でしょうか。
テキストの「$${r=0.82-0.91}$$」よりも値が大きくなっています。
以下、確認的因子分析の結果を記録として残しておきます。
■ 確認的因子分析の結果:4つの因子のサマリー
### 確認的因子分析の結果:4つの因子の結果表示
# Est.Stdは標準偏回帰係数
inspect_cfa = model_cfa.inspect(std_est=True)
display(inspect_cfa.iloc[70:80].round(3))【実行結果】

■ パス図
ファイル名「model_cfa.png」で作業フォルダにパス図の画像ファイルを保存します。
### 確認的因子分析の結果:推定後のパス係数付きパス図の出力
# 共分散を表示する、標準化係数を表示する
g = semopy.semplot(model_cfa, 'model_cfa.png', plot_covs=True, std_ests=True)
display(g)【実行結果】

以上でベイズ分析前の各種分析は終わりです。

ベイズモデルの構築
尺度別に4つのモデルを作成しますが、分析対象データが異なる点を除くと、モデルの内容は全て同じです。
モデルの数式表現
目指したいPyMCのモデルの「なんちゃって数式」表記です。
$$
\begin{align*}
\alpha &\sim \text{LogNormal}\ (\text{mu}=0,\ \text{sigma}=2,\ \text{dims}=item) \\
\kappa &\sim \text{Normal} (\text{mu}=[-0.1, 0, 0.1], \text{sigma}=10,\ \text{ordered},\ \text{dims}=(item,\ cutpoint)) \\
\theta &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=1,\ \text{dims}=id) \\
likelihood &\sim \text{OrderedLogistic}\ (\text{eta}=\alpha[itemIdx] \times \theta[idIdx],\ \text{cutpoints}=\kappa[itemIdx, :\ ]) \\
\end{align*}
$$
では4つの尺度ごとにベイズモデルを作ってまいります。
1.SDS
(1) モデルの定義
数式表現を実直にモデル記述します。
### モデルの定義:SDS
## データの準備:分析対象尺度の抽出
# 尺度SDSのデータを抽出
data_in = data[data['尺度']=='SDS'].reset_index(drop=True)
# 項目番号のインデックス化(0始まりにする)
data_in['項目番号'] = data_in['項目番号'] - 1
# 項目番号の要素数
num_item = data_in['項目番号'].nunique()
# 得点の範囲を0~3に揃える:SDSのみの処理
data_in['得点'] = data_in['得点'] - 1
# 得点の要素数
num_score = data_in['得点'].nunique()
## モデルの定義
with pm.Model() as model_sds:
### coordの定義
# データのインデックス
model_sds.add_coord('data', values=data_in.index, mutable=True)
# 回答者ID stan:N, i
model_sds.add_coord('id', values=sorted(data_in['回答者ID'].unique()),
mutable=True)
# 項目番号 stan:J, j
model_sds.add_coord('item', values=sorted(data_in['項目番号'].unique()),
mutable=True)
# カットポイント stan:3
model_sds.add_coord('cutpoint', values=list(range(num_score - 1)),
mutable=True)
### dataの定義
# 目的変数:得点U_ij
y = pm.ConstantData('y', value=data_in['得点'].values, dims='data')
# 回答者IDのインデックス
idIdx = pm.ConstantData('idIdx', value=data_in['回答者ID'].values,
dims='data')
# 項目番号のインデックス
itemIdx = pm.ConstantData('itemIdx', value=data_in['項目番号'].values,
dims='data')
### 事前分布
## a_j = 識別力母数
alpha = pm.LogNormal('alpha', mu=0, sigma=2, dims='item')
## κ_jk = 識別力母数α_j × カテゴリ困難度母数b_jk
# ※muにcutpointの数(3)のパラメータを指定したら行単位のorederdが効いた
kappa = pm.Normal('kappa', mu=[-0.1, 0, 0.1], sigma=10,
dims=('item', 'cutpoint'),
transform=pm.distributions.transforms.ordered)
## θ_i = 抑うつ度
theta = pm.Normal('theta', mu=0, sigma=1, dims='id')
### 尤度:順序ロジスティック分布
likelihood = pm.OrderedLogistic('likelihood',
eta=alpha[itemIdx] * theta[idIdx],
cutpoints=kappa[itemIdx, :],
compute_p=False,
observed=y, dims='data')【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の4つを設定しました。データの行の座標:名前「data」、値「行インデックス」
回答者の座標:名前「id」、値「回答者ID」
項目番号の座標:名前「item」、値「項目番号」
カットポイントの座標:名前「cutpoint」、値「尺度得点(最大得点を除く)」
因子負荷行列のうち自由推定する要素の座標:名前「Z1」、値「Z1のインデックス」
dataの定義
次の3つを設定しました。得点:y (目的変数、回答者の回答値)
回答者IDのインデックス:idIdx
項目番号のインデックス:itemIdx
パラメータの事前分布
モデルの数式表現どおりです。
$${\kappa}$$の順序制約(ordered)
正規分布の平均パラメータに3つ(カットポイントの数)の値を小さい順で与えたら、transform引数で指定した順序制約(ordered)が効きました!
尤度
順序ロジスティック分布です。
(2) モデルの外観の確認
### モデルの表示
model_sds【実行結果】
シンプルな構造ですね。

### モデルの可視化
pm.model_to_graphviz(model_sds)【実行結果】

(3) 事後分布からのサンプリング
乱数生成数はテキストよりも少ないです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ10分でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 10分20秒
# テキスト: iter=2000, warmup=?, chains=4
with model_sds:
idata_sds = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.8,
nuts_sampler='numpyro', random_seed=1234)【実行結果】省略
(4) サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$とします。
ここでは$${\hat{R} > 1.01}$$のパラメータが無いことを確認します。
### r_hat>1.1の確認
# 設定
idata_in = idata_sds # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
(az.rhat(idata_in) > threshold).sum()【実行結果】
$${\hat{R} > 1.01}$$のパラメータは0件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
pm.summary(idata_sds, hdi_prob=0.95, round_to=3)【実行結果】

トレースプロットで事後分布サンプリングデータの様子を確認します。
一部のパラメータに限定して表示しています。
### トレースプロットの表示
pm.plot_trace(idata_sds, compact=False)
plt.tight_layout();【実行結果】
左のグラフから、4本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。

(5) 推論データの保存
推論データを再利用する(かもしれない)場合に備えてファイルに保存しましょう。
idata_sds をpickleで保存します。
### idataの保存 pickle
file = r'idata_sds_ch17.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_sds, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata_sds_ch17.pkl'
with open(file, 'rb') as f:
idata_sds_load = pickle.load(f)
2.CES-D
(1) モデルの定義
数式表現を実直にモデル記述します。
### モデルの定義:CESD
## データの準備:分析対象尺度の抽出
# 尺度CESDのデータを抽出
data_in = data[data['尺度']=='CESD'].reset_index(drop=True)
# 項目番号のインデックス化(0始まりにする)
data_in['項目番号'] = data_in['項目番号'] - 1
# 項目番号の要素数
num_item = data_in['項目番号'].nunique()
# 得点の範囲を0~3に揃える:SDSのみの処理
# data_in['得点'] = data_in['得点'] - 1
# 得点の要素数
num_score = data_in['得点'].nunique()
## モデルの定義
with pm.Model() as model_cesd:
### coordの定義
# データのインデックス
model_cesd.add_coord('data', values=data_in.index, mutable=True)
# 回答者ID stan:N, i
model_cesd.add_coord('id', values=sorted(data_in['回答者ID'].unique()),
mutable=True)
# 項目番号 stan:J, j
model_cesd.add_coord('item', values=sorted(data_in['項目番号'].unique()),
mutable=True)
# カットポイント stan:3
model_cesd.add_coord('cutpoint', values=list(range(num_score - 1)),
mutable=True)
### dataの定義
# 目的変数:得点U_ij
y = pm.ConstantData('y', value=data_in['得点'].values, dims='data')
# 回答者IDのインデックス
idIdx = pm.ConstantData('idIdx', value=data_in['回答者ID'].values,
dims='data')
# 項目番号のインデックス
itemIdx = pm.ConstantData('itemIdx', value=data_in['項目番号'].values,
dims='data')
### 事前分布
## a_j = 識別力母数
alpha = pm.LogNormal('alpha', mu=0, sigma=2, dims='item')
## κ_jk = 識別力母数α_j × カテゴリ困難度母数b_jk
# ※muにcutpointの数(3)のパラメータを指定したら行単位のorederdが効いた
kappa = pm.Normal('kappa', mu=[-0.1, 0, 0.1], sigma=10,
dims=('item', 'cutpoint'),
transform=pm.distributions.transforms.ordered)
## θ_i = 抑うつ度
theta = pm.Normal('theta', mu=0, sigma=1, dims='id')
### 尤度:順序ロジスティック分布
likelihood = pm.OrderedLogistic('likelihood',
eta=alpha[itemIdx] * theta[idIdx],
cutpoints=kappa[itemIdx, :],
compute_p=False,
observed=y, dims='data')【モデル注釈】省略
(2) モデルの外観の確認
### モデルの表示
model_cesd【実行結果】

### モデルの可視化
pm.model_to_graphviz(model_cesd)【実行結果】

(3) 事後分布からのサンプリング
乱数生成数はテキストよりも少ないです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ3分でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 3分
# テキスト: iter=2000, warmup=?, chains=4
with model_cesd:
idata_cesd = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1234)【実行結果】省略
(4) サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$とします。
ここでは$${\hat{R} > 1.01}$$のパラメータが無いことを確認します。
### r_hat>1.1の確認
# 設定
idata_in = idata_cesd # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
$${\hat{R} > 1.01}$$のパラメータは0件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
pm.summary(idata_cesd, hdi_prob=0.95, round_to=3)【実行結果】

トレースプロットで事後分布サンプリングデータの様子を確認します。
一部のパラメータに限定して表示しています。
### トレースプロットの表示
pm.plot_trace(idata_cesd, compact=False)
plt.tight_layout();【実行結果】
左のグラフから、4本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。

(5) 推論データの保存
推論データを再利用する(かもしれない)場合に備えてファイルに保存しましょう。
idata_cesd をpickleで保存します。
### idataの保存 pickle
file = r'idata_cesd_ch17.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_cesd, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata_cesd_ch17.pkl'
with open(file, 'rb') as f:
idata_cesd_load = pickle.load(f)
3.BDI-II
(1) モデルの定義
数式表現を実直にモデル記述します。
### モデルの定義:BDI
## データの準備:分析対象尺度の抽出
# 尺度BDIのデータを抽出
data_in = data[data['尺度']=='BDI'].reset_index(drop=True)
# 項目番号のインデックス化(0始まりにする)
data_in['項目番号'] = data_in['項目番号'] - 1
# 項目番号の要素数
num_item = data_in['項目番号'].nunique()
# 得点の範囲を0~3に揃える:SDSのみの処理
# data_in['得点'] = data_in['得点'] - 1
# 得点の要素数
num_score = data_in['得点'].nunique()
## モデルの定義
with pm.Model() as model_bdi:
### coordの定義
# データのインデックス
model_bdi.add_coord('data', values=data_in.index, mutable=True)
# 回答者ID stan:N, i
model_bdi.add_coord('id', values=sorted(data_in['回答者ID'].unique()),
mutable=True)
# 項目番号 stan:J, j
model_bdi.add_coord('item', values=sorted(data_in['項目番号'].unique()),
mutable=True)
# カットポイント stan:3
model_bdi.add_coord('cutpoint', values=list(range(num_score - 1)),
mutable=True)
### dataの定義
# 目的変数:得点U_ij
y = pm.ConstantData('y', value=data_in['得点'].values, dims='data')
# 回答者IDのインデックス
idIdx = pm.ConstantData('idIdx', value=data_in['回答者ID'].values,
dims='data')
# 項目番号のインデックス
itemIdx = pm.ConstantData('itemIdx', value=data_in['項目番号'].values,
dims='data')
### 事前分布
## a_j = 識別力母数
alpha = pm.LogNormal('alpha', mu=0, sigma=2, dims='item')
## κ_jk = 識別力母数α_j × カテゴリ困難度母数b_jk
# ※muにcutpointの数(3)のパラメータを指定したら行単位のorederdが効いた
kappa = pm.Normal('kappa', mu=[-0.1, 0, 0.1], sigma=10,
dims=('item', 'cutpoint'),
transform=pm.distributions.transforms.ordered)
## θ_i = 抑うつ度
theta = pm.Normal('theta', mu=0, sigma=1, dims='id')
### 尤度:順序ロジスティック分布
likelihood = pm.OrderedLogistic('likelihood',
eta=alpha[itemIdx] * theta[idIdx],
cutpoints=kappa[itemIdx, :],
compute_p=False,
observed=y, dims='data')【モデル注釈】省略
(2) モデルの外観の確認
### モデルの表示
model_bdi【実行結果】

### モデルの可視化
pm.model_to_graphviz(model_cesd)【実行結果】

(3) 事後分布からのサンプリング
乱数生成数はテキストよりも少ないです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ4分でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 4分20秒
# テキスト: iter=2000, warmup=?, chains=4
with model_bdi:
idata_bdi = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1234)【実行結果】省略
(4) サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$とします。
ここでは$${\hat{R} > 1.01}$$のパラメータが無いことを確認します。
### r_hat>1.1の確認
# 設定
idata_in = idata_bdi # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
$${\hat{R} > 1.01}$$のパラメータは0件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
pm.summary(idata_bdi, hdi_prob=0.95, round_to=3)【実行結果】

トレースプロットで事後分布サンプリングデータの様子を確認します。
一部のパラメータに限定して表示しています。
### トレースプロットの表示
pm.plot_trace(idata_bdi, compact=False)
plt.tight_layout();【実行結果】
左のグラフから、4本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。

(5) 推論データの保存
推論データを再利用する(かもしれない)場合に備えてファイルに保存しましょう。
idata_bdi をpickleで保存します。
### idataの保存 pickle
file = r'idata_bdi_ch17.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_bdi, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata_bdi_ch17.pkl'
with open(file, 'rb') as f:
idata_bdi_load = pickle.load(f)
4.PHQ-9
(1) モデルの定義
数式表現を実直にモデル記述します。
### モデルの定義:PHQ9
## データの準備:分析対象尺度の抽出
# 尺度PHQ9のデータを抽出
data_in = data[data['尺度']=='PHQ9'].reset_index(drop=True)
# 項目番号のインデックス化(0始まりにする)
data_in['項目番号'] = data_in['項目番号'] - 1
# 項目番号の要素数
num_item = data_in['項目番号'].nunique()
# 得点の範囲を0~3に揃える:SDSのみの処理
# data_in['得点'] = data_in['得点'] - 1
# 得点の要素数
num_score = data_in['得点'].nunique()
## モデルの定義
with pm.Model() as model_phq9:
### coordの定義
# データのインデックス
model_phq9.add_coord('data', values=data_in.index, mutable=True)
# 回答者ID stan:N, i
model_phq9.add_coord('id', values=sorted(data_in['回答者ID'].unique()),
mutable=True)
# 項目番号 stan:J, j
model_phq9.add_coord('item', values=sorted(data_in['項目番号'].unique()),
mutable=True)
# カットポイント stan:3
model_phq9.add_coord('cutpoint', values=list(range(num_score - 1)),
mutable=True)
### dataの定義
# 目的変数:得点U_ij
y = pm.ConstantData('y', value=data_in['得点'].values, dims='data')
# 回答者IDのインデックス
idIdx = pm.ConstantData('idIdx', value=data_in['回答者ID'].values,
dims='data')
# 項目番号のインデックス
itemIdx = pm.ConstantData('itemIdx', value=data_in['項目番号'].values,
dims='data')
### 事前分布
## a_j = 識別力母数
alpha = pm.LogNormal('alpha', mu=0, sigma=2, dims='item')
## κ_jk = 識別力母数α_j × カテゴリ困難度母数b_jk
# ※muにcutpointの数(3)のパラメータを指定したら行単位のorederdが効いた
kappa = pm.Normal('kappa', mu=[-0.1, 0, 0.1], sigma=10,
dims=('item', 'cutpoint'),
transform=pm.distributions.transforms.ordered)
## θ_i = 抑うつ度
theta = pm.Normal('theta', mu=0, sigma=1, dims='id')
### 尤度:順序ロジスティック分布
likelihood = pm.OrderedLogistic('likelihood',
eta=alpha[itemIdx] * theta[idIdx],
cutpoints=kappa[itemIdx, :],
compute_p=False,
observed=y, dims='data')【モデル注釈】省略
(2) モデルの外観の確認
### モデルの表示
model_phq9【実行結果】

### モデルの可視化
pm.model_to_graphviz(model_phq9)【実行結果】

(3) 事後分布からのサンプリング
乱数生成数はテキストよりも少ないです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ1分でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 1分20秒
# テキスト: iter=2000, warmup=?, chains=4
with model_phq9:
idata_phq9 = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.8,
nuts_sampler='numpyro', random_seed=1234)【実行結果】省略
(4) サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$とします。
ここでは$${\hat{R} > 1.01}$$のパラメータが無いことを確認します。
### r_hat>1.1の確認
# 設定
idata_in = idata_phq9 # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
$${\hat{R} > 1.01}$$のパラメータは0件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
pm.summary(idata_phq9, hdi_prob=0.95, round_to=3)【実行結果】

トレースプロットで事後分布サンプリングデータの様子を確認します。
一部のパラメータに限定して表示しています。
### トレースプロットの表示
pm.plot_trace(idata_phq9, compact=False)
plt.tight_layout();【実行結果】
左のグラフから、4本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。

(5) 推論データの保存
推論データを再利用する(かもしれない)場合に備えてファイルに保存しましょう。
idata_phq9 をpickleで保存します。
### idataの保存 pickle
file = r'idata_phq9_ch17.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_phq9, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata_phq9_ch17.pkl'
with open(file, 'rb') as f:
idata_phq9_load = pickle.load(f)
ベイズ分析
1.項目反応カテゴリ特性曲線
テキストのベイズ分析は、得られた母数に基づいて各尺度・各項目の項目反応カテゴリ特性曲線を描き、各項目の特徴を検討することからはじまります。
項目反応カテゴリ特性曲線を算出する関数と描画する関数を定義します。
算出する関数はテキストの R スクリプトのロジックを引用させていただきました。
### 項目反応カテゴリ特性曲線の算出関数の定義 ※テキストのRスクリプトを引用
def calc_crf(alpha, kappa):
x = np.arange(-3, 3.1, 0.1)
ruiseki1 = (1 / (1 + np.exp(-1 * alpha.reshape(-1, 1) * x
+ kappa[:, 0].reshape(-1, 1)))) # カテゴリ2以上に反応する確率
ruiseki2 = (1 / (1 + np.exp(-1 * alpha.reshape(-1, 1) * x
+ kappa[:, 1].reshape(-1, 1)))) # カテゴリ3以上に反応する確率
ruiseki3 = (1 / (1 + np.exp(-1 * alpha.reshape(-1, 1) * x
+ kappa[:, 2].reshape(-1, 1)))) # カテゴリ4以上に反応する確率
crf1 = 1 - ruiseki1 # カテゴリ1に反応する確率
crf2 = ruiseki1 - ruiseki2 # カテゴリ2に反応する確率
crf3 = ruiseki2 - ruiseki3 # カテゴリ3に反応する確率
crf4 = ruiseki3 - 0 # カテゴリ4に反応する確率
result = np.stack((crf1, crf2, crf3, crf4))
return result # shape=(4, 20, 1000)### 項目反応カテゴリ特性曲線の描画関数の定義
def plot_crf(crf, title): # crf.shape=(4, 20, 1000)
# x軸の値の作成
x = np.arange(-3, 3.1, 0.1)
# 描画領域の設定
fig = plt.figure(figsize=(15, 18))
# 項目ごとにaxes描画を繰り返し処理(i=項目index)
for i in range(crf.shape[1]):
# axesの作成
ax = plt.subplot(6, 4, i+1)
# カテゴリごとにaxes描画を繰り返し処理(j=カテゴリindex)
for j in range(crf.shape[0]):
ax.plot(x, crf[j, i, :], label=f'カテゴリ{j+1}')
# 修飾
ax.set(title=f'項目{i+1}', xlabel='抑うつ度 $\\theta$', ylabel='確率',
ylim=(-0.1, 1.1), yticks=(0, 0.2, 0.4, 0.6, 0.8, 1.0))
ax.grid(lw=0.3)
# 凡例の取得
if i==0:
handles, labels = ax.get_legend_handles_labels()
# 全体修飾
plt.suptitle(f'{title} の項目反応カテゴリ特性曲線', y=1.02, fontsize=16)
fig.legend(handles=handles, labels=labels,
loc='upper center', bbox_to_anchor=(0.5, 1.0), ncol=4)
plt.tight_layout()
plt.show();4つの尺度の項目反応カテゴリ特性曲線を描画します。
テキストは4本引かれるカテゴリ別の曲線の中で、異質なカテゴリが無いかを確認しています。
描画した曲線は概ねテキストの異質性の確認どおりになっていると思います(テキストに図の掲載が無いため、正解かどうかが分からない状態です)。
(1) SDS
### SDSの項目反応カテゴリ特性曲線の描画
# パラメータalpha, kappaのサンプルデータの平均値を算出
alpha_mean_sds = (idata_sds.posterior.alpha.stack(sample=('chain', 'draw'))
.mean(axis=1).data)
kappa_mean_sds = (idata_sds.posterior.kappa.stack(sample=('chain', 'draw'))
.mean(axis=2).data)
# 項目反応カテゴリ特性曲線の算出
crf_sds = calc_crf(alpha_mean_sds, kappa_mean_sds)
# 項目反応カテゴリ特性曲線の描画
plot_crf(crf_sds, 'SDS')【実行結果】

(2) CES-D
### CESDの項目反応カテゴリ特性曲線の描画
# パラメータalpha, kappaのサンプルデータの平均値を算出
alpha_mean_cesd = (idata_cesd.posterior.alpha.stack(sample=('chain', 'draw'))
.mean(axis=1).data)
kappa_mean_cesd = (idata_cesd.posterior.kappa.stack(sample=('chain', 'draw'))
.mean(axis=2).data)
# 項目反応カテゴリ特性曲線の算出
crf_cesd = calc_crf(alpha_mean_cesd, kappa_mean_cesd)
# 項目反応カテゴリ特性曲線の描画
plot_crf(crf_cesd, 'CES-D')【実行結果】

(3) BDI-II
### BDIの項目反応カテゴリ特性曲線の描画
# パラメータalpha, kappaのサンプルデータの平均値を算出
alpha_mean_bdi = (idata_bdi.posterior.alpha.stack(sample=('chain', 'draw'))
.mean(axis=1).data)
kappa_mean_bdi = (idata_bdi.posterior.kappa.stack(sample=('chain', 'draw'))
.mean(axis=2).data)
# 項目反応カテゴリ特性曲線の算出
crf_bdi = calc_crf(alpha_mean_bdi, kappa_mean_bdi)
# 項目反応カテゴリ特性曲線の描画
plot_crf(crf_bdi, 'BDI-II')【実行結果】

(4) PHQ-9
### PHQ9の項目反応カテゴリ特性曲線の描画
# パラメータalpha, kappaのサンプルデータの平均値を算出
alpha_mean_phq9 = (idata_phq9.posterior.alpha.stack(sample=('chain', 'draw'))
.mean(axis=1).data)
kappa_mean_phq9 = (idata_phq9.posterior.kappa.stack(sample=('chain', 'draw'))
.mean(axis=2).data)
# 項目反応カテゴリ特性曲線の算出
crf_phq9 = calc_crf(alpha_mean_phq9, kappa_mean_phq9)
# 項目反応カテゴリ特性曲線の描画
plot_crf(crf_phq9, 'PHQ-9')【実行結果】


2.テスト情報量曲線(TIC)
テスト情報量 TI は抑うつ度の推定精度を表す指標となっているそうです。
テキストの図17.1に相当します。
項目情報量を算出する関数を定義します。
テキストの R スクリプトのロジックを引用させていただきました。
### 項目情報量IIFの算出関数の定義 ※テキストのRスクリプトを引用
def calc_iif(alpha, kappa):
# alphaの形状を(n, 1)に変換
alpha = alpha.copy().reshape(-1, 1)
# x軸の値の設定
x = np.arange(-3, 3.1, 0.1)
# カテゴリn以上に反応する確率の算出 n=(1, 2, 3, 4, 5)
ruiseki1 = np.ones(len(x)) # カテゴリ1以上に反応する確率=1
ruiseki2 = (1 / (1 + np.exp(-1 * alpha * x + kappa[:, 0].reshape(-1, 1))))
ruiseki3 = (1 / (1 + np.exp(-1 * alpha * x + kappa[:, 1].reshape(-1, 1))))
ruiseki4 = (1 / (1 + np.exp(-1 * alpha * x + kappa[:, 2].reshape(-1, 1))))
ruiseki5 = np.zeros(len(x)) # カテゴリ5以上に反応する確率=0
# カテゴリnに反応する確率の算出 n=(1, 2, 3, 4)
CRF1 = ruiseki1 - ruiseki2 # カテゴリ0に反応する確率
CRF2 = ruiseki2 - ruiseki3 # カテゴリ1に反応する確率
CRF3 = ruiseki3 - ruiseki4 # カテゴリ2に反応する確率
CRF4 = ruiseki4 - ruiseki5 # カテゴリ3に反応する確率
# カテゴリnに反応する確率の微分 n=(1, 2, 3, 4)
bibun1 = alpha * (ruiseki1 * (1 - ruiseki1) - ruiseki2 * (1 - ruiseki2))
bibun2 = alpha * (ruiseki2 * (1 - ruiseki2) - ruiseki3 * (1 - ruiseki3))
bibun3 = alpha * (ruiseki3 * (1 - ruiseki3) - ruiseki4 * (1 - ruiseki4))
bibun4 = alpha * (ruiseki4 * (1 - ruiseki4) - ruiseki5 * (1 - ruiseki5))
# カテゴリnのカテゴリ情報量の算出 n=(1, 2, 3, 4)
CIF1 = bibun1**2 / CRF1 # カテゴリ0のカテゴリ情報量
CIF2 = bibun2**2 / CRF2 # カテゴリ1のカテゴリ情報量
CIF3 = bibun3**2 / CRF3 # カテゴリ2のカテゴリ情報量
CIF4 = bibun4**2 / CRF4 # カテゴリ3のカテゴリ情報量
# 項目情報量の算出
IIF = CIF1 + CIF2 + CIF3 + CIF4
return IIF4つの尺度のテスト情報量を算出します。
### テスト情報量TIFの算出
tif_phq9 = calc_iif(alpha_mean_phq9, kappa_mean_phq9).sum(axis=0)
tif_bdi = calc_iif(alpha_mean_bdi, kappa_mean_bdi).sum(axis=0)
tif_cesd = calc_iif(alpha_mean_cesd, kappa_mean_cesd).sum(axis=0)
tif_sds = calc_iif(alpha_mean_sds, kappa_mean_sds).sum(axis=0)【実行結果】なし
描画します。
### テスト情報量の描画 ★図17.1に相当
# x軸の値の設定
xval = np.arange(-3, 3.1, 0.1)
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 5))
# PHQ-9のテスト情報量曲線の描画
ax.plot(xval, tif_phq9, ls='-', label='PHQ-9')
# BDI-IIのテスト情報量曲線の描画
ax.plot(xval, tif_bdi, ls='--', label='BDI-II')
# CES-Dのテスト情報量曲線の描画
ax.plot(xval, tif_cesd, ls=':', lw=2, label='CES-D')
# SDSのテスト情報量曲線の描画
ax.plot(xval, tif_sds, ls='-.', label='SDS')
# 修飾
ax.set(xlabel='抑うつ度 $\\theta$', ylabel='テスト情報量 $TI$',
title='テスト情報量曲線')
plt.legend()
plt.grid(lw=0.5);【実行結果】
テスト情報量曲線によって、抑うつ度の高い(低い)回答者の抑うつ度の推定に向いている尺度を検討できるそうです。
テキストの通り、CES-D、BDI-II、PHQ-9が近い傾向になっており、比較的抑うつ度の高い人の推定精度が高くなると考えられます。
SDSは比較的抑うつ度の低い人の推定精度が高くなると考えられます。


3.相対効率曲線(REC)
相対曲線 RE は2つの尺度の TI の比です。
相対効率曲線を活用することで、尺度間の測定効率の比較を抑うつ度の核水準において可能になるそうです。
テキストの図17.2、図17.3に相当します。
4つの尺度の相対効率 RE を算出します。
### 相対効率REの算出
bdi_vs_phq9 = tif_bdi / tif_phq9
cesd_vs_phq9 = tif_cesd / tif_phq9
sds_vs_phq9 = tif_sds / tif_phq9
cesd_vs_bdi = tif_cesd / tif_bdi
sds_vs_bdi = tif_sds / tif_bdi
sds_vs_cesd = tif_sds / tif_cesd【実行結果】なし
CES-D, BDI-II, PHQ-9間の REC を描画します。
### CES-D, BDI-II, PHQ-9の相対効率曲線の描画 ★図17.2に相当
# x軸の値の設定
xval = np.arange(-3, 3.1, 0.1)
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 5))
# bdi/phq9の相対効率曲線の描画
ax.plot(xval, bdi_vs_phq9, ls='-', label='BDI-II / PHQ-9')
# cesd/phq9の相対効率曲線の描画
ax.plot(xval, cesd_vs_phq9, ls='-.', label='CES-D / PHQ-9')
# cesd/bdiのテスト情報量曲線の描画
ax.plot(xval, cesd_vs_bdi, ls='--', label='CES-D / BDI-II')
# 修飾
ax.set(xlabel='抑うつ度 $\\theta$', ylabel='相対効率 $RE$',
title='CES-D, BDI-II, PHQ-9間の相対効率曲線')
plt.legend()
plt.grid(lw=0.5);【実行結果】
BDI-II / PHQ-9 の比較では、縦軸の相対効率 RE が項目数の比率 21 / 9 = 2.33 よりも大きい抑うつ度($${\theta_i \leq 2.97,\ 2.47 \leq \theta_i}$$)のとき、BDI-II の方が測定効率が高い、と読むようです。

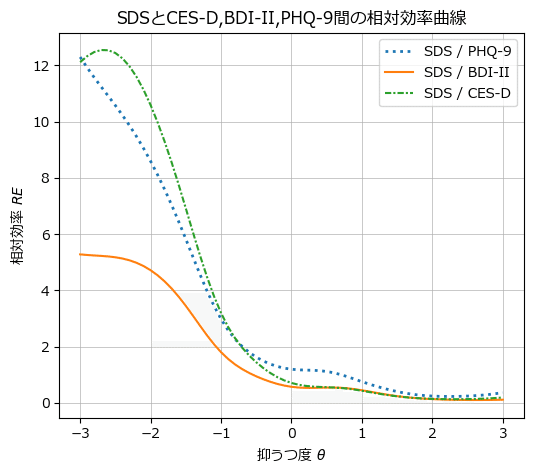
SDSと他の尺度の間の REC を描画します。
### SDSとCES-D, BDI-II, PHQ-9の相対効率曲線の描画 ★図17.3に相当
# x軸の値の設定
xval = np.arange(-3, 3.1, 0.1)
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 5))
# sds/phq9の相対効率曲線の描画
ax.plot(xval, sds_vs_phq9, ls=':', lw=2, label='SDS / PHQ-9')
# sds/bdiの相対効率曲線の描画
ax.plot(xval, sds_vs_bdi, ls='-', label='SDS / BDI-II')
# sds/cesdのテスト情報量曲線の描画
ax.plot(xval, sds_vs_cesd, ls=(0, (3, 1, 1, 1)), label='SDS / CES-D')
# 修飾
ax.set(xlabel='抑うつ度 $\\theta$', ylabel='相対効率 $RE$',
title='SDSとCES-D,BDI-II,PHQ-9間の相対効率曲線')
plt.legend()
plt.grid(lw=0.5);【実行結果】

4.尺度得点間の換算表
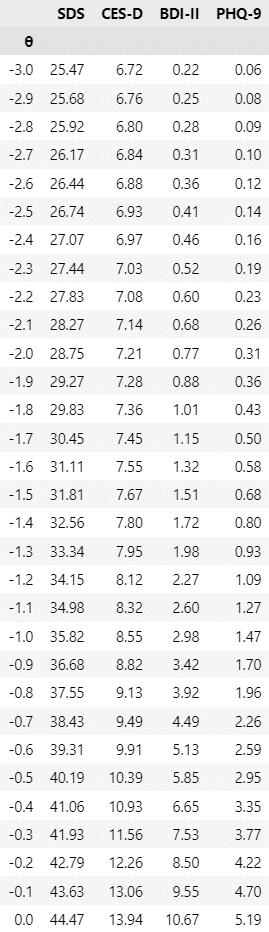
抑うつ度$${\theta_i}$$が-3~3の範囲で、4つの尺度の尺度得点の期待値を算出した「換算表」を作成します。
テキストの表17.1です。
### 尺度得点間の換算表の作成 ★表17.1に相当
# θの値の設定
theta_val = np.arange(-3, 3.1, 0.1).round(1)
# 尺度得点の期待値とTCFの算出 ★テキストのRスクリプトに準拠
expected_phq9 = np.array([
(np.arange(0, 4).reshape(-1, 1) * crf_phq9[:, i, :]).sum(axis=0)
for i in range(9)])
tcf_phq9 = expected_phq9.sum(axis=0)
expected_bdi = np.array([
(np.arange(0, 4).reshape(-1, 1) * crf_bdi[:, i, :]).sum(axis=0)
for i in range(21)])
tcf_bdi = expected_bdi.sum(axis=0)
expected_cesd = np.array([
(np.arange(0, 4).reshape(-1, 1) * crf_cesd[:, i, :]).sum(axis=0)
for i in range(20)])
tcf_cesd = expected_cesd.sum(axis=0)
expected_sds = np.array([(
np.arange(1, 5).reshape(-1, 1) * crf_sds[:, i, :]).sum(axis=0)
for i in range(20)])
tcf_sds = expected_sds.sum(axis=0)
# データフレーム化
tcf_df = pd.DataFrame({'θ': theta_val,
'SDS': tcf_sds,
'CES-D': tcf_cesd,
'BDI-II': tcf_bdi,
'PHQ-9': tcf_phq9,
}).set_index('θ', drop=True)
# データフレームの表示
pd.set_option('display.max_rows', 100)
display(tcf_df.round(2))【実行結果】
概ねテキストの換算表の値と一致しています。

換算表を可視化しましょう。
### テスト特性曲線の描画
tcf_df.plot(kind='line', figsize=(6, 5), xlabel='抑うつ度 $\\theta$',
ylabel='尺度得点の期待値', title='テスト特性曲線')
plt.grid(lw=0.5)【実行結果】

以上で第17章は終了です。
おわりに
項目反応理論
書籍「たのしいベイズモデリング」シリーズを実践することで、項目反応理論のベイズモデルに多数ふれあう機会をいただきました。
特性値を示す潜在変数$${\theta}$$、項目の識別力$${\alpha}$$と困難度$${\beta}$$に加えて、今回新たに出現した$${\kappa}$$。
回答値(実際値)から潜在変数が浮き彫りになることが痛快で、とても楽しく取り組むことができました。
また、特性値$${\theta}$$の大小に対応する反応確率をプロットする項目特性曲線の曲線美にも惹かれます。
日常的に利用する手法ではないかもですが、ときどき思い出したい手法です。

おわり
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
