
第16章「消費者トレンドをつかまえろ」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング2」の第16章「消費者トレンドをつかまえろ」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
今回も章タイトルのインパクトが強いですね!
この章は観光地名のWeb検索量をベイズ動的因子分析モデルで分析します。
~因子と観光地の関連性から国内観光の隠れた消費者トレンドを見つける~
深淵なる言葉たちが飛び交う書面空間で迷子になりました(汗)
よって今回の PyMC化 はテキストの結果を再現できなかったです(泣)

それはさておき、PyMCのベイズモデリングの世界を楽しんでまいりましょう!
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 小野滋 先生
モデル難易度: ★★★★★ (難しい)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★・・・ & いまいち \\
結果再現度 & ★★・・・ & やや悪い \\
楽しさ & ★★★★・ & 楽しそう \\
\end{array}
$$

評価ポイント
テキストの推論結果と異なっています。
PyMCの勝手モデルと因子回転のどちらかでミスが生じていると思うのですが、原因を特定できていません。
改善点を見出すことができなくて、とてももどかしいです。
工夫・喜び・反省
動的因子分析の理解に乏しいことが原因となり、Python&PyMCの実装にとても苦労しました。
特に次の2点の実装に時間がかかってしまいました。PyMCモデル内の因子負荷行列の実装
Rスクリプトの sub_Rotate_Stan.1 関数の「DFAの因子を回転する」処理の実装。特にバリマックス回転の実現

モデルの概要
テキストの調査・実験の概要
■ 分析の概要
一言でまとめると、
$$
\begin{array}{l:l}
① データ &観光地名の検索量の時系列データを \\
② モデル & 動的因子分析モデルに当てはめて \\
③ ターゲット & 背後にある国内観光の消費者トレンドを探る \\
\end{array}
$$
です。
■ 観光地名の検索量の時系列データ
著者の先生は、Google トレンドで以下の条件を満たす377地名の週次検索量時系列データ(261週)を取得しています。
・期間は2014年から2018年
・検索カテゴリは「旅行」
・地域は「日本」
・検索ワードは先生がWikipediaから取得した377地名
ただし、実際に分析に用いるのは 50 の観光地に限定され、検索量には季節調整とデータの標準化を施しています。
■ 動的因子分析モデル
動的因子分析は多数の時系列の背後に少数の隠れた時系列があると想定できるときに適した分析手法、と先生はまとめています。
時系列データの背後に隠れた時系列(因子時系列)を想定し、観測変数に対する潜在変数の重み(因子負荷)を想定するモデルです。
ここまでの流れを図示します。

テキストのモデリング
■ 目的変数と関心のあるパラメータ
目的変数は週$${t}$$における地名$${i}$$の標準化済み検索量$${y_{it}}$$です。
関心のあるパラメータはおそらく因子負荷$${b_{ik}}$$だと思われます。
■ モデル数式
動的因子分析モデルです。詳しいことはぜひテキストで確かめてください!
$$
\begin{align*}
y_{it} &= \displaystyle \sum_{k=1}^K b_{ik} f_{kt} + \sum_{s=1}^4 \left( c_{is} \sin \left( 2 \pi s\ \cfrac{261}{365/7} \right) + d_{is} \cos \left( 2 \pi s\ \cfrac{261}{365/7} \right) \right) + e_{it} \\
\\
f_{k0} &= 0 \\
f_{kt} &= f_{k,t-1} + a_{it} \\
a_{it} &\sim \text{Normal}\ (0,\ 1) \\
\\
i &= 1, \dots, K, k=1+1, \dots, K について b_{ik}=0 \\
i &= 1, \dots, K について b_{ii} \geq 0 \\
\\
e_{it} &\sim \text{Normal}\ (0,\ \sigma^2_y)
\end{align*}
$$
【変数・記号の概要】
$${K}$$は$${y_{it}}$$の背後の時系列の本数
$${b_{ik}}$$は因子負荷
$${f_{kt}}$$は因子時系列
右辺第二項はフーリエ級数項
$${e_{it}}$$は撹乱項

■分析・分析結果
PyMCモデル勝手案の推論結果はテキストと大きく乖離しています。
推定値を用いた分析内容はぜひテキストでご確認ください。
PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.インポート
### インポート
# 数値・確率計算
import pandas as pd
import numpy as np
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# varimax回転
from factor_analyzer import FactorAnalyzer
# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
# ユーティリティ
import pickle
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')
2.データの読み込みと前処理
csvファイル「dfData2.csv」をpandasのデータフレームに読み込みます。
### データの読み込み
data_orgn = pd.read_csv('dfData2.csv', encoding='shift-jis')
data_orgn['date'] = pd.to_datetime(data_orgn['date'])
data_orgn.columns = ['観光地ID', '日付', '検索量', '観光地名', '季節調整量',
'季節調整後検索量']
display(data_orgn)【実行結果】
98136行、6列の大きなデータです。
項目内容の概要です。
・観光地ID:観光地のID
・日付:検索が行われた週
・検索量:Google が算定した検索に関する値
・観光地名:観光地の名前
・季節調整量:季節調整のベースにする値
・季節調整後検索量:季節調整量で調整した検索量


3.データの概観の確認
要約統計量を確認しましょう。
### 要約統計量の表示
data_orgn.describe().round(2)【実行結果】
検索量は0から100の値のようです。

データに含まれる観光地の数をカウントしてみます。
### 観光地(keyword)の数
print(f'観光地数: {data_orgn["観光地名"].nunique()}')【実行結果】
376です。

時系列の検索量のイメージを3つの観光地で掴みましょう。
テキストの図16.1に相当します。
### 検索量データの例示描画 ※図16.1に相当
# 表示対象の観光地名のリスト
places = ['秋葉原', '屋久島', '江差']
# 描画領域の指定
fig, ax = plt.subplots(1, 3, figsize=(10, 4), sharex=True, sharey=True)
# 観光地ごとに描画を繰り返し処理
for i, place in enumerate(places):
# 観光地の日付と検索量を一時データフレームに格納
tmp = data_orgn[data_orgn['観光地名']==place][['日付', '検索量']]
# 折れ線グラフの描画
ax[i].plot(tmp['日付'], tmp['検索量'], lw=0.7)
# 修飾(axes単位)
ax[i].grid(lw=0.3)
ax[i].set(title=f'{place}')
# 修飾(fig単位)
fig.supxlabel('週次')
fig.supylabel('検索量')
plt.tight_layout();【実行結果】
観光地によって検索量の大きさや傾向は異なるようです。


4.分析対象の観光地を絞り込みとデータの前処理
テキスト 16.4.3節「分析対象の決定」にならって「検索量の合計」と「検索量の変動」の両方が大きい 50 観光地を抽出します。
まずは、検索量の合計・標準偏差、季節調整後の検索量の標準偏差を算出します。
### 分析対象の観光地を特定するためのデータの集計
# 観光地単位の検索量の合計・標準偏差、季節調整後の検索量の標準偏差を算出
data_sum = (data_orgn.groupby(by=['観光地ID', '観光地名'])
.agg({'検索量': ['sum', 'std'], '季節調整後検索量': ['std']}))
# 列名の変更:項目名_統計量名
data_sum.columns = ['_'.join(col).strip() for col in data_sum.columns]
# インデックスのリセット:マルチインデックスを解除
data_sum.reset_index(inplace=True)
# データフレームの表示
display(data_sum)【実行結果】

検索量の合計と季節調整後検索量の標準偏差(変動)の分布を可視化します。
テキストの図16.2に相当します。
### 検索量の合計と変動の分布の描画 ※図16.2に相当
# 描画領域の指定
plt.figure(figsize=(10, 7))
ax = plt.subplot()
# 分析対象のゾーン(ピンク)の描画
ax.fill_between(x=[10000, 20000], y1=11.75, y2=25, color='lightpink', alpha=0.5)
# 散布図の描画
ax.scatter(x=data_sum['検索量_sum'], y=data_sum['季節調整後検索量_std'],
color='blue', s=10)
# 観光地名の描画:annotateでscatterの点(x,y)の傍に観光地textを添える
for (text, x, y) in data_sum[['観光地名', '検索量_sum',
'季節調整後検索量_std']].values:
ax.annotate(text=text, xy=(x+100, y-0.2), alpha=0.7)
# 修飾
ax.text(x=14500, y=23, s='【分析対象ゾーン】', fontsize=16)
ax.set(xlabel='検索量合計', ylabel='季節調整後の検索量SD',xlim=(1500, 20000),
ylim=(3, 25), yticks=range(5, 26, 5))
ax.grid(lw=0.5)
plt.show()【実行結果】
薄赤色のゾーンに当てはまる観光地が分析対象になります。
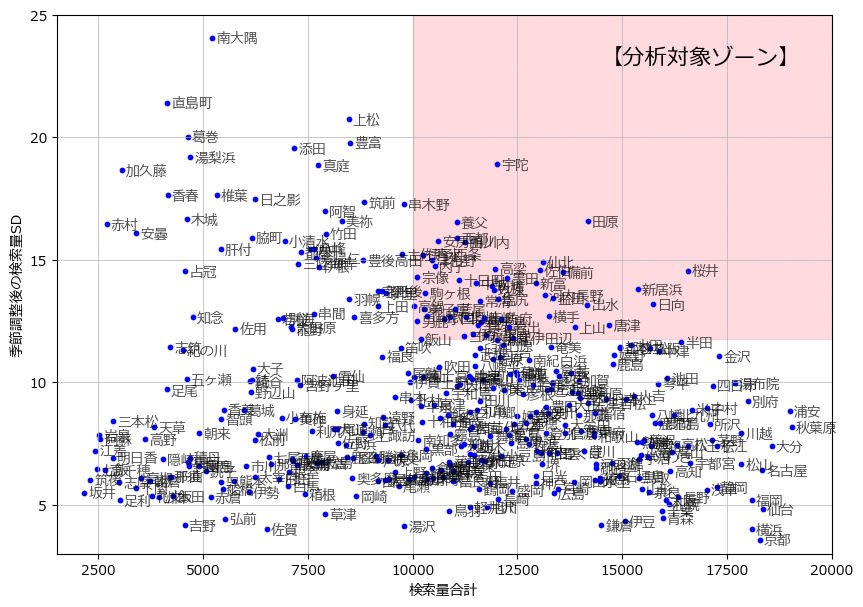
では、50観光地を抽出して分析用データを作成しましょう。
観光地の抽出とデータの標準化を行います。
### データの前処理1:観測データdata_orgnから50の観光地を抽出
## 観光地ID・日付の縦持ちデータフレームの作成
# 検索量合計>10000 かつ 季節調整後の検索量SD>11.75の観光地を抽出
data_melt = data_sum.query('検索量_sum > 10000 & 季節調整後検索量_std > 11.75')
# 抽出した観光地に該当する観測データdata_orgn(日付別)を取得
data_melt = pd.merge(data_melt[['観光地ID', '観光地名']], data_orgn,
on=['観光地ID', '観光地名'], how='left')
display(data_melt)
## 観光地IDを横持ちに変換
# pivot_table()で横持ちに変換
data = data_melt.pivot_table(index=['日付'], columns=['観光地ID'],
values=['検索量']).reset_index(drop=True)
# 列のマルチインデックスを解除(1行目の列名を削除)
data.columns = data.columns.droplevel(0)
display(data)
## データ標準化
data_std = (data - data.mean()) / data.std()
display(data_std.round(3))【実行結果】最終形のみ表示
行が週(時系列)、列が観光地IDです。

フーリエ級数項を作成します。
### データの前処理2:共変量としてモデルに投入するフーリエ級数項の作成
# フーリエ級数項の列名の設定
tmp_colnames = [f'フーリエ{i}' for i in range(1, 9)]
# 式16.4第二項のフーリエ級数項の算出
t = np.arange(1, len(data)+1)
tmp_sin = np.array([np.sin(2*np.pi*s*t/(365/7)) for s in range(1, 5)]).T
tmp_cos = np.array([np.cos(2*np.pi*s*t/(365/7)) for s in range(1, 5)]).T
# データフレーム化
data_fourier = pd.DataFrame(np.hstack([tmp_sin, tmp_cos]), columns=tmp_colnames)
# データフレームの表示
display(data_fourier)【実行結果】
左4列が sin 、右4列が cos です。


モデルの構築以降、Pythonコードの元になるテキストの R スクリプトと Stan コードを読み解いたつもりですが、読み誤りやPythonコードへの変換誤りなどが含まれている可能性が多分にあります。
予めご了承くださいませ。

モデルの構築
テキストにならって因子数8のモデルを作成します。
モデルの数式表現
目指したいPyMCのモデルの「なんちゃって数式」表記です。
$$
\begin{align*}
init\_dist &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=1)\\
mgX &\sim \text{GaussianRandomWalk}\ (\text{mu}=0,\ \text{sigma}=1,\ \text{init\_dist}=init\_dist,\ dims=(factor,\ time))\\
mgZ &= 因子負荷行列、省略 \\
mgBeta &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=1,\ dims=(place,\ fourier) \\
gSigma &\sim \text{HalfNormal}\ (\text{nu}=3,\ \text{sigma}=2)\\
mgPred &= mgZ @ mgX + mgBeta @ mgC,\ dims=(place,\ time) \\
likelihood &\sim \text{Normal}\ (\text{mu}=mgPred,\ \text{sigma}=gSigma,\ dims=(place,\ time)) \\
\end{align*}
$$

1.モデルの定義
数式表現を実直にモデル記述します。
変数名はテキストの Stan コードと比較・チェックしやすくする目的で、Stan コードの変数名にほぼ合わせました。
変数「mgZto8」は苦肉の策です。。。
### モデルの定義
## 初期値設定
num_factor = 8 # 因子数
factor_labels = list(range(1, num_factor+1)) # 因子数のインデックス
num_place = len(data_std.columns) # 観光地の数
num_agZfree = int((num_factor**2 - num_factor) / 2 # 自由因子の数
+ (num_place - num_factor) * num_factor)
num_agZfree_idx = list(range(num_agZfree)) # 自由因子のインデックス
### モデルの定義
with pm.Model() as model:
### coordの定義
# 時間(週):要素数216
model.add_coord('time', values=data_std.index.values, mutable=True)
# 観光地:要素数50
model.add_coord('place', values=data_std.columns.values, mutable=True)
# 共変量(フーリエ級数):要素数8
model.add_coord('fourier', values=data_fourier.columns.values,
mutable=True)
# 因子:要素数8
model.add_coord('factor', values=factor_labels, mutable=True)
# 因子負荷行列のうち自由推定する要素:要素数364
model.add_coord('Z1', values=num_agZfree_idx, mutable=True)
### dataの定義
# 目的変数:観光地・時間(週)ごとの検索量(stan:mgY)
y = pm.ConstantData('y', value=data_std.T.values, dims=('place', 'time'))
# 共変量(フーリエ級数)(stan:mgC)
mgC = pm.ConstantData('mgC', value=data_fourier.T.values,
dims=('fourier', 'time'))
### 事前分布
## 因子時系列mgX(数式:f_kt)
init_dist = pm.Normal.dist(mu=0, sigma=1)
mgX = pm.GaussianRandomWalk('mgX', mu=0, sigma=1, init_dist=init_dist,
dims=('factor', 'time'))
## 因子負荷行列(数式:b_ik)
# 因子負荷のうち自由推定する要素(制約なし・ベクトル)
agZfree = pm.Normal('agZfree', mu=0, sigma=1, dims='Z1')
# 因子負荷のうち自由推定する要素(正値制約つき、ベクトル)
agZposi = pm.HalfNormal('agZposi', sigma=1, dims='factor')
# 因子負荷行列の上8×8行列の作成(0値制約、posi正値制約、free制約なしを考慮)
mgZto8 = pt.stacklists([
[agZposi[0], 0, 0, 0, 0, 0, 0, 0],
[agZfree[0], agZposi[1], 0, 0, 0, 0, 0, 0],
[agZfree[1], agZfree[2], agZposi[2], 0, 0, 0, 0, 0],
[agZfree[3], agZfree[4], agZfree[5], agZposi[3], 0, 0, 0, 0],
[agZfree[6], agZfree[7], agZfree[8], agZfree[9], agZposi[4], 0, 0, 0],
[agZfree[10], agZfree[11], agZfree[12], agZfree[13], agZfree[14], agZposi[5], 0, 0],
[agZfree[15], agZfree[16], agZfree[17], agZfree[18], agZfree[19], agZfree[20], agZposi[6], 0],
[agZfree[21], agZfree[22], agZfree[23], agZfree[24], agZfree[25], agZfree[26], agZfree[27], agZposi[7]],
])
# 因子負荷行列の9行目以降の行列の作成
mgZafter9 = agZfree[28:].reshape((num_place - num_factor, num_factor))
# 因子負荷行列の完成(mgZto8とmgZafter9を行方向に結合)
mgZ = pm.Deterministic('mgZ', pt.concatenate([mgZto8, mgZafter9], axis=0),
dims=('place', 'factor'))
# 共変量の係数(数式:c_is, d_is)
mgBeta = pm.Normal('mgBeta', mu=0, sigma=1, dims=('place', 'fourier'))
# 撹乱項の標準偏差gSigma(数式:σ_y)
gSigma = pm.HalfStudentT('gSigma', nu=3, sigma=2)
# 目的変数の予測値
mgPred = pm.Deterministic('mgPred', mgZ @ mgX + mgBeta @ mgC,
dims=('place', 'time'))
## 尤度
likelihood = pm.Normal('likelihood', mu=mgPred, sigma=gSigma, observed=y,
dims=('place', 'time'))【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の5つを設定しました。時間(週)の座標:名前「time」、値「行インデックス」
観光地の座標:名前「place」、値「観光地ID」
フーリエ項の座標:名前「fourier」、値「フーリエ項の列名」
因子の座標:名前「factor」、値「因子のインデックス」
因子負荷行列のうち自由推定する要素の座標:名前「Z1」、値「Z1のインデックス」
dataの定義
次の2つを設定しました。検索量:y (目的変数)
フーリエ級数:mgC(共変量)
パラメータの事前分布
モデルの数式表現どおりです(因子負荷行列が難解でスミマセン)。
尤度
正規分布です。

2.モデルの外観の確認
### モデルの表示
model【実行結果】

### モデルの可視化 40秒
pm.model_to_graphviz(model)【実行結果】
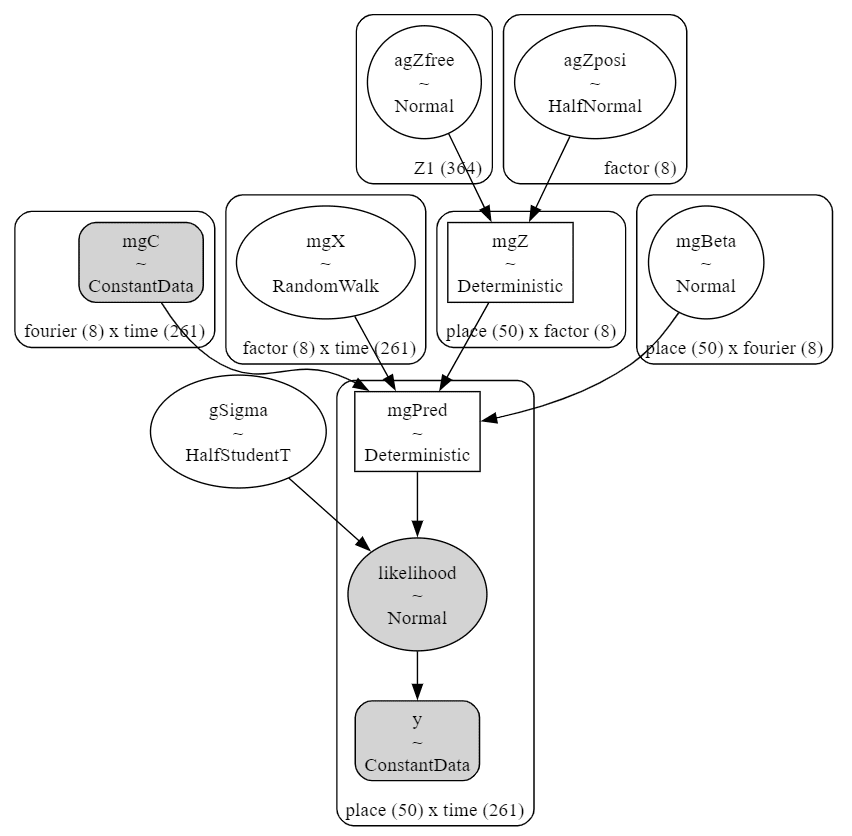

3.事後分布からのサンプリング
乱数生成数はテキストよりも少ないです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ5分でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 5分
# テキスト: iter=3000, warmup=1000, chains=2, adapt_delta=0.99, max_treedepth=15
with model:
idata = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.8,
nuts_sampler='numpyro', random_seed=123)【実行結果】省略

4.サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$とします。
ここでは$${\hat{R} > 1.02}$$のパラメータが無いことを確認します。
### r_hat>1.1の確認
# 設定
idata_in = idata # idata名
threshold = 1.02 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
$${\hat{R} > 1.02}$$のパラメータは0件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。
ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示 1分10秒
pm.summary(idata, hdi_prob=0.95, round_to=3)【実行結果】

トレースプロットで事後分布サンプリングデータの様子を確認します。
一部のパラメータに限定して表示しています。
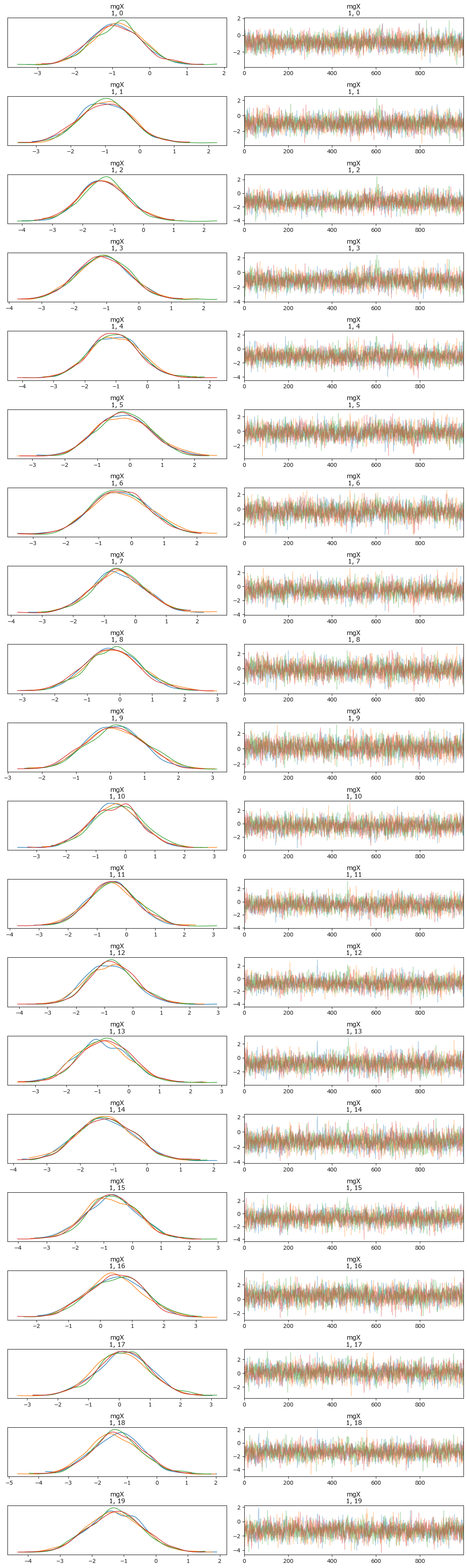
### トレースプロットの表示
pm.plot_trace(idata, compact=False)
plt.tight_layout();【実行結果】
左のグラフから、4本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。

5.推論データの保存
推論データを再利用する(かもしれない)場合に備えてファイルに保存しましょう。
idata をpickleで保存します。
### idataの保存 pickle
file = r'idata_ch16.pkl'
with open(file, 'wb') as f:
pickle.dump(idata, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata_ch16.pkl'
with open(file, 'rb') as f:
idata_load = pickle.load(f)
分析のためのデータ加工
1.DFAの因子を回転
最大の難敵「回転」に取り掛かります。
バリマックス回転には factor_analyzer ライブラリの FactorAnalyzer を利用しました。
テキストの R スクリプトに記述された「sub_Rotate_Stan.1」関数を完コピしたつもりですが、処理結果がテキストと異なるので、この処理のどこかに誤りがある可能性があります。
### DFAの因子を回転する ※sub_Rotate_Stan.1 30秒
# 作成する変数★
# mgZ_mean, mgX_mean, mgZ_mean_rotated, mgX_mean_rotated,
# mgZ_rotated, mgX_rotated, mgZ_rotated_mean, mgX_rotated_mean
# 事後分布サンプリングデータからmgZとmgXを取り出し
mgZ_sample = idata.posterior.mgZ.stack(sample=('chain', 'draw')).data
mgX_sample = idata.posterior.mgX.stack(sample=('chain', 'draw')).data
print('mgZ_sample.shape: ', mgZ_sample.shape)
print('mgX_sample.shape: ', mgX_sample.shape)
# mgZとmgXの平均値を算出
mgZ_mean = mgZ_sample.mean(axis=2) # ★
mgX_mean = mgX_sample.mean(axis=2) # ★
print('mgZ_mean.shape: ', mgZ_mean.shape)
print('mgX_mean.shape: ', mgX_mean.shape)
# mgZとmgXの平均値をバリマックス回転
fa = FactorAnalyzer(n_factors=8, rotation='varimax')
fa.fit(mgZ_mean)
mgRotMat = fa.rotation_matrix_ # 回転行列
mgZ_mean_rotated = mgZ_mean @ mgRotMat # ★
mgX_mean_rotated = np.linalg.inv(mgRotMat) @ mgX_mean # ★
print('mgZ_mean_rotated.shape: ', mgZ_mean_rotated.shape)
print('mgX_mean_rotated.shape: ', mgX_mean_rotated.shape)
# mgZとmgXの事後分布サンプリングデータをバリマックス回転
nNumMCMC = mgZ_sample.shape[2] # 4000
nNumSeries = mgZ_sample.shape[0] # 50
nNumFactor = mgZ_sample.shape[1] # 8
nNumTime = mgX_sample.shape[1] # 261
mgZ_rotated = np.zeros((nNumMCMC, nNumSeries, nNumFactor))
mgX_rotated = np.zeros((nNumMCMC, nNumFactor, nNumTime))
for i in range(nNumMCMC):
mgCurrentZ = mgZ_sample[:, :, i]
mgCurrentX = mgX_sample[:, :, i]
fa = FactorAnalyzer(n_factors=8, rotation='varimax')
fa.fit(mgCurrentZ)
mgRotMat = fa.rotation_matrix_
mgCurrentZ_rotated = mgCurrentZ @ mgRotMat
mgCurrentX_rotated = np.linalg.inv(mgRotMat) @ mgCurrentX
mgZ_rotated[i, :, :] = mgCurrentZ_rotated # ★
mgX_rotated[i, :, :] = mgCurrentX_rotated # ★
print('mgZ_rotated.shape: ', mgZ_rotated.shape)
print('mgX_rotated.shape: ', mgX_rotated.shape)
mgZ_rotated_mean = mgZ_rotated.mean(axis=0) # ★
mgX_rotated_mean = mgX_rotated.mean(axis=0) # ★
print('mgZ_rotated_mean.shape: ', mgZ_rotated_mean.shape)
print('mgX_rotated_mean.shape: ', mgX_rotated_mean.shape)【実行結果】

2.因子と地名の関連性
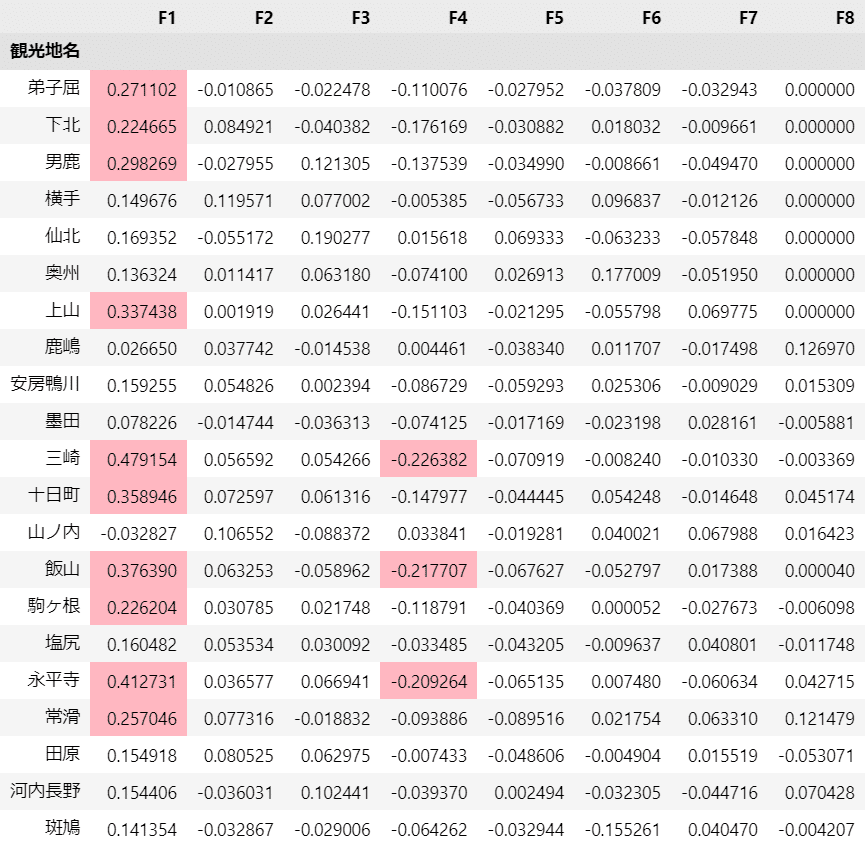
出来上がったデータの因子負荷「mgZ_mean_rotated」の絶対値が 0.2 以上の観光地をハイライトで表示します。
テキストの表16.1に相当します。
### 因子負荷の絶対値が0.2以上である観光地名の表示 ※表16.1に相当
# ★ただしテキストの結果と合致していない
# 観光地名の取得
query = '検索量_sum > 10000 & 季節調整後検索量_std > 11.75'
place50 = data_sum.query(query)['観光地名'].values
# 観光地名と回転後因子負荷と結合してデータフレームを作成
columns = ['観光地名'] + [f'F{i}' for i in range(1, 9)]
mgZ_mean_rotated_df = pd.DataFrame(
np.c_[place50, mgZ_mean_rotated], columns=columns
).set_index('観光地名')
# 絶対値が0.2以上の因子負荷のセルに色をつけて表示
display(mgZ_mean_rotated_df.style.map(
lambda x: 'background-color: lightpink' if abs(x)>=0.2 else ''))【実行結果】
赤色のセルが絶対値 0.2 以上の箇所です。
因子F1はテキストの結果と似ている感じがします。
その他の因子はテキストの結果と乖離しています。


3.因子時系列の描画
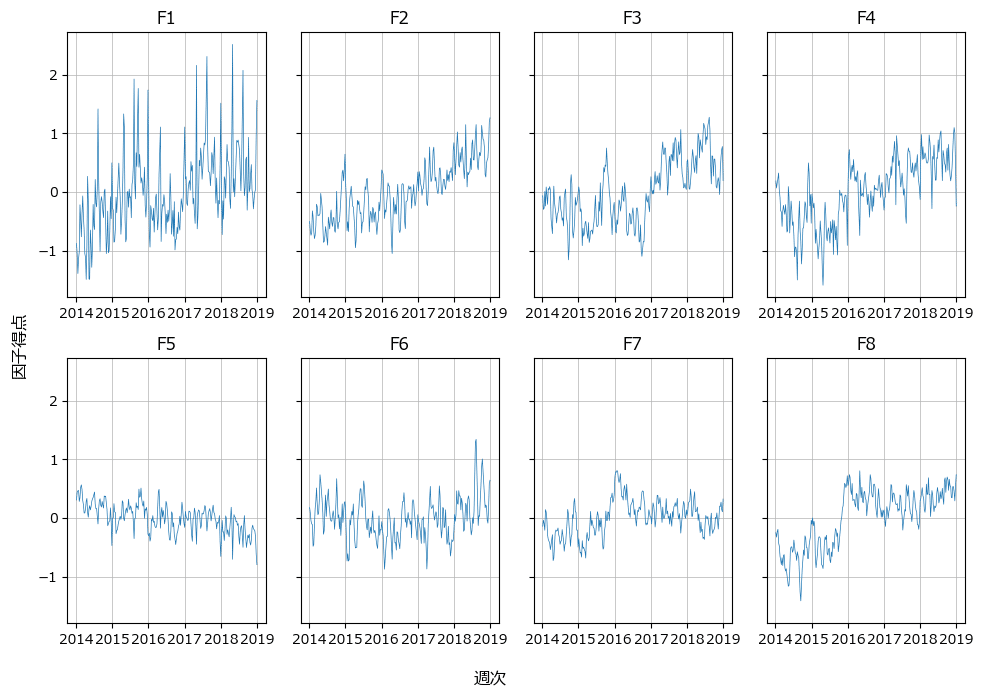
8つの因子時系列を可視化します。
テキストの図16.3に相当します。
### 因子時系列の描画 ※図16.3に相当 ★ただしテキストの結果と合致していない
fig, ax = plt.subplots(2, 4, figsize=(10, 7), sharey=True)
for i in range(8):
pos = divmod(i, 4)
ax[pos].plot(data_orgn['日付'].unique(), mgX_mean_rotated[i], lw=0.5)
ax[pos].set(title=f'F{i+1}')
ax[pos].grid(lw=0.5)
fig.supxlabel('週次')
fig.supylabel('因子得点')
plt.tight_layout();【実行結果】
テキストの結果似ている因子時系列もあれば、全く異なる因子時系列もあります。
4.因子F1とF4の観光地の検索量時系列データを可視化
テキストの図16.4、図16.5に相当する検索量時系列データの描画です。
まずは飯山、永平寺、津和野です。カッコ内は因子F1の因子負荷です。
### 検索量データの例示描画 ※図16.4に相当
# 表示対象の観光地名のリスト
places = ['飯山', '永平寺', '津和野']
# 描画領域の指定
fig, ax = plt.subplots(1, 3, figsize=(10, 4), sharex=True, sharey=True)
# 観光地ごとに描画を繰り返し処理
for i, place in enumerate(places):
# 観光地の日付と検索量を一時データフレームに格納
tmp = data_orgn[data_orgn['観光地名']==place][['日付', '検索量']]
# 折れ線グラフの描画
ax[i].plot(tmp['日付'], tmp['検索量'], lw=0.7)
# タイトルの描画 因子負荷を併記
val = mgZ_mean_rotated_df[mgZ_mean_rotated_df.index==place]['F1'].values[0]
ax[i].set(title=f'{place} ({val:+.2f})')
# 修飾(axes単位)
ax[i].grid(lw=0.3)
# 修飾(fig単位)
fig.supxlabel('週次')
fig.supylabel('検索量')
plt.tight_layout();【実行結果】

続いて横手、伊万里、宇佐です。カッコ内は因子F4の因子負荷です。
F4の因子負荷の値はテキストの結果と大きく乖離しています。
### 検索量データの例示描画 ※図16.5に相当
# 表示対象の観光地名のリスト
places = ['横手', '伊万里', '宇佐']
# 描画領域の指定
fig, ax = plt.subplots(1, 3, figsize=(10, 4), sharex=True, sharey=True)
# 観光地ごとに描画を繰り返し処理
for i, place in enumerate(places):
# 観光地の日付と検索量を一時データフレームに格納
tmp = data_orgn[data_orgn['観光地名']==place][['日付', '検索量']]
# 折れ線グラフの描画
ax[i].plot(tmp['日付'], tmp['検索量'], lw=0.7)
# タイトルの描画 因子負荷を併記
val = mgZ_mean_rotated_df[mgZ_mean_rotated_df.index==place]['F4'].values[0]
ax[i].set(title=f'{place} ({val:+.2f})')
# 修飾(axes単位)
ax[i].grid(lw=0.3)
# 修飾(fig単位)
fig.supxlabel('週次')
fig.supylabel('検索量')
plt.tight_layout();【実行結果】

今回はデータ加工までに留めて、分析・解釈には立ち入らないようにします。
以上で第16章は終了です。
おわりに
因子分析
過去にお試し程度で因子分析に触れた経験があります。
答えが掲載されていてコードミスを見つけやすい環境でした。
今回の動的因子分析モデルはテキストに答えがあると言っても、モデルの複雑さや回転処理等の難しさなどが要因となり、個人的に答え合わせがしにくい状況でした。
どなたか、この記事のPython&PyMCに潜む「誤り因子」を推論していただけませんか?

おわり
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
