
【Pythonで統計モデル】因子分析5:確認的因子分析
はじめに
株式会社GA technologiesの福中です。今、僕は、Advanced Innovation Strategy Center(以下AISC)という部署でChief Data Scientistとして働いています(詳しい自己紹介はAISC WEBサイトのプロフィールをご覧ください)。前回に引き続き、【Pythonで統計モデル】というシリーズの記事を書いていこうと思います。前回はカテゴリカル変数を含んだ場合の因子分析であるカテゴリカル因子分析を、Pythonを使って実行する方法について解説しました。
第5回目である今回は確認的因子分析(Confirmatory Factor Analysis: CFA)もPythonで実行可能であることを確認していきます。
注意点
本記事は統計学およびPythonの初心者向け解説記事ではありません。普段からR等を使って統計モデルによる分析や研究を行っている研究者の方が、改めてPythonで因子分析を行う必要が出た際のリファレンスとしての利用を想定しています。したがって、因子分析に不慣れな方は、先に以下で紹介するテキストをはじめとした初心者用の教科書で勉強するとよいと思います。
テキスト
本記事では東京図書から出版されている因子分析入門―Rで学ぶ最新データ解析―の分析結果を、Pythonを使って再現していきます。分析用データは東京図書のホームページからダウンロードできますので、興味のある方はぜひ試してみてください。
環境
本記事の分析は、OS: Windows 11、Python 3.11.2の環境下で行っています。また、必要なパッケージは以下となります。インストール済みの方は割愛してください。
# packageのインストール
pip install numpy pandas matplotlib japanize_matplotlib
pip install graphviz
pip install semopyなおsemopyは構造方程式モデリング(Structural Equation Modeling: SEM )を行うためのパッケージで、ドキュメントは以下にあります。
本記事ではここから重要な部分をいくつかピックアップしてご紹介します。網羅的な解説はしませんので、適宜、必要に応じてご参照ください。
確認的因子分析の概要
これまでの全4回にわたる因子分析の記事では主に探索的因子分析(EFA)について述べてきました。EFAとは、各観測変数がすべての因子から影響を受けているモデルを想定し、回転(rotaiton)とよばれる因子負荷量の変換を通じて単純構造を見つけ出すことを主目的としています。
それに対して確認的因子分析(CFA)とは、特定の因子から特定の観測変数への影響をあらかじめ想定しておき、それ以外の観測変数への影響はないものとして分析する手法です。いうなれば、自身の頭の中にある単純構造をそのままダイレクトにモデルに反映して、モデルとデータとの乖離を検証するアプローチになります。ゆえに、EFAがデータドリブンなアプローチに対して、CFAは仮説検証型のアプローチともいえます。
確認的因子分析(CFA)は「因子分析」という名はついていますが、現代では構造方程式モデリング(SEM)の下位モデルとしてとらえるのが一般的です。したがって、CFA単体のパッケージやアプリは(おそらく)存在せず、SEMのパッケージ等を使って分析モデルを構築していくことになります。つまり、CFAで分析モデルを作るためには、まず最初にSEMで出てくる概念や約束事を学ぶ必要があることに注意してください。Pythonのsemopyというパッケージも、SEM特有のモデル表現のための文法(シンタックス)が用意されています。Mplusやlavaanなど、SEMのアプリやパッケージを一度でも使ったことがある人なら特に抵抗なく受け入れられると思います。特にsemopyはlavaanライクに作られているので、lavaan経験者にはとても相性が良いと思います。しかし、初めての人にはすごくとっつきにくい印象を持つでしょう。そのような方はsemopyのマニュアルを読み解こうとするよりも、以下のようなSEMの入門書を先に読んだ方が理解が早いかもしれません。
データの読み込み
それではデータの読み込みから始めましょう。テキスト第9章で例として使われてたデータは、「因子分析2:探索的因子分析の実践」の記事でも使った以下のようなスキー場データです。このデータはC. E. Osgoodによって提唱されたSD(Semantic Differential)法を用いて測定された、24個のスキー場(コンセプト)に対する9個の形容詞対への評定結果です。各回答はすべて7件法によって測定されています。
# packageの読み込み
import numpy as np
import pandas as pd
import semopy# スキー場データの読み込み
SDdat = pd.read_csv("dat/ski.csv", encoding='shift_jis', index_col=0)
SDdat.head()
このままでも良いのですが、テキストに合わせて列名を変更しておきましょう。以下のように変更しておけば、CFAモデルのシンタックスを書く際にも書きやすくなります。
# 列名の変更
SDdat.columns = ['x1', 'x2', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x9']
SDdat.head()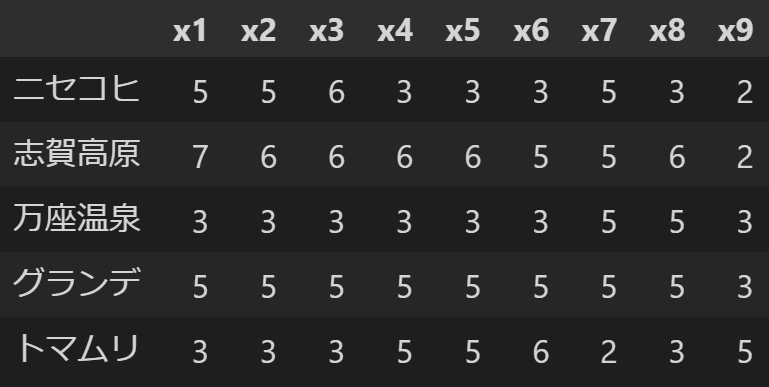
確認的因子分析モデルのシンタックスの書き方
それでは確認的因子分析を行うためのシンタックスを書いてみましょう。が、その前に、今回のモデルの模式図を確認しておきましょう。今回のモデルは以下のような形になります。なお誤差因子(独自因子)から影響は省略してあります。
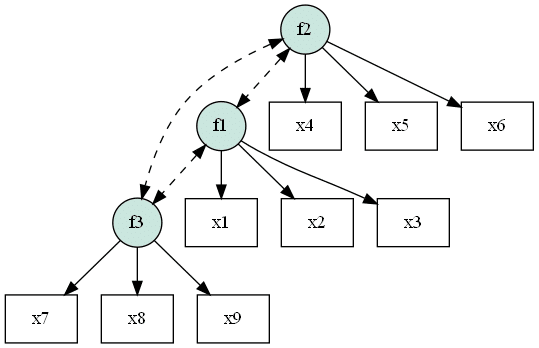
ポイントは以下の点になります。
3因子を想定し、因子間にはすべて相関関係を仮定する
f1因子はx1~x3の変数のみに影響している
f2因子はx4~x6の変数のみに影響している
f3因子はx7~x9の変数のみに影響している
この条件をsemopyのシンタックスで表現すると以下のようになります。
# 確認的因子分析モデルのシンタックス
mod = """
f1 =~ x1 + x2 + x3
f2 =~ x4 + x5 + x6
f3 =~ x7 + x8 + x9
"""ここで"=~" は測定方程式の演算子(Measurement operator)になります。今回でいうと、観測変数の背後に潜在変数を仮定したい場合に指定する演算子と理解しておけばよいでしょう。semopyはSEMのパッケージなので、これ以外にも様々な演算子が存在するのですが、今回はCFAに焦点を当てているため割愛します。このあたりのSEMによる分析の仕方については、そのうち別のシリーズとしてブログにしていきたいので、その際に詳しく説明したいと思います。
次に、因子間相関についてです。上記を見ると因子間相関の記述が見られませんが、実はこれで自動的に設定されています。このあたりはMplusの流儀に倣っていて、熟練者にとってはとても便利ですね。しかし、初学者にとっては混乱のもとになっているようなので、注意しておきましょう。もし因子間相関を0、すなわち直交解を仮定したい場合は以下のように共分散を0に制約することで対処します。
# 因子間相関を0に制約したい場合のシンタックス
mod = """
f1 =~ x1 + x2 + x3
f2 =~ x4 + x5 + x6
f3 =~ x7 + x8 + x9
f1 ~~ 0*f2
f1 ~~ 0*f3
f2 ~~ 0*f3
"""ここで"~~"は共分散演算子(Covariance operator)で、変数間に相関関係を仮定したい場合に指定します。また、"*"を使用することで、その変数間を”*”の直前の数値で制約することができます。今回でいうと、すべての因子間相関を仮定し、その推定値を0で制約していることになります。
それでは確認的因子分析を実行しましょう。なお、以下では因子間相関を仮定した場合のモデルで分析を実行しているので注意してください。
# 確認的因子分析の実行
model = semopy.Model(mod)
result = model.fit(SDdat)分析の結果を出力します。なお、ここでは標準化解も出力したいので、inspectメソッドの引数に"std_est=True"を指定します。
# 標準化解を含む結果の出力
inspect = model.inspect(std_est=True)
print(inspect) lval op rval Estimate Est. Std Std. Err z-value p-value
0 x1 ~ f1 1.000000 0.936776 - - -
1 x2 ~ f1 0.934586 0.993933 0.079553 11.747919 0.0
2 x3 ~ f1 0.821509 0.932197 0.0909 9.037472 0.0
3 x4 ~ f2 1.000000 0.978843 - - -
4 x5 ~ f2 0.907637 0.941490 0.083506 10.869189 0.0
5 x6 ~ f2 0.726299 0.915366 0.07646 9.499045 0.0
6 x7 ~ f3 1.000000 0.969800 - - -
7 x8 ~ f3 0.786791 0.874773 0.107178 7.340978 0.0
8 x9 ~ f3 -0.872685 -0.907384 0.106615 -8.1854 0.0
9 f3 ~~ f3 3.057743 1.000000 0.956077 3.198219 0.001383
10 f3 ~~ f1 -0.599338 -0.183668 0.696271 -0.860783 0.389357
11 f3 ~~ f2 -1.081089 -0.370787 0.656111 -1.647723 0.09941
12 f2 ~~ f2 2.780177 1.000000 0.843926 3.294336 0.000987
13 f1 ~~ f1 3.482376 1.000000 1.14222 3.048778 0.002298
14 f1 ~~ f2 1.085217 0.348773 0.690038 1.572691 0.11579
15 x1 ~~ x1 0.485918 0.122450 0.178158 2.727462 0.006382
16 x6 ~~ x6 0.283733 0.162105 0.100417 2.825534 0.00472
17 x4 ~~ x4 0.121482 0.041866 0.114174 1.064004 0.287327
18 x7 ~~ x7 0.193401 0.059487 0.198718 0.973246 0.330431
19 x5 ~~ x5 0.293516 0.113597 0.123616 2.374417 0.017577
20 x9 ~~ x9 0.499640 0.176654 0.205272 2.434034 0.014932
21 x8 ~~ x8 0.580732 0.234772 0.205862 2.820984 0.004788
22 x3 ~~ x3 0.354311 0.131009 0.126333 2.804572 0.005038
23 x2 ~~ x2 0.037245 0.012097 0.09632 0.386682 0.698991Estimateの列を見るとわかるように、パス係数の値がテキストP232の表9.2の推定値の欄と小数点第2位の精度で一致していることがわかります。
また、モデルのデータへの当てはまりの良さを確認するための適合度指標を出力してみましょう。スクリプトは以下の通りです。
# 適合度の出力
stats = semopy.calc_stats(model)
print(stats.T) Value
DoF 24.000000
DoF Baseline 36.000000
chi2 26.414344
chi2 p-value 0.332482
chi2 Baseline 280.847431
CFI 0.990139
GFI 0.905948
AGFI 0.858922
NFI 0.905948
TLI 0.985209
RMSEA 0.066135
AIC 39.798805
BIC 64.537935
LogLik 1.100598GFI、AGFI、AIC、BICの値がテキストの結果と異なりますが、それ以外は概ね一致しています。テキストにも書いてありますが、GFI、AGFI、AIC、BICの定義式はいくつかあり、semopyとテキストでその定義が異なるからです。特に理由がなければ、上記の結果をそのまま採用して問題ありません。
最後に推定した結果のパス係数をつけて、パス図を描いてみましょう。なんとsemopyにはパス図を描画する機能まで準備されています。
# 推定後のパス係数付きパス図の出力
g = semopy.semplot(model, "model_est.png", plot_covs=True, std_ests=True, show=True)
最後に
いかがでしたでしょうか?全5回にわたり、【Pythonで統計モデル】シリーズ第1弾因子分析編の記事を書いてきましたが、「Pythonが統計モデルに弱い」と言われていたのはもはや過去のものになっていたことがわかると思います。2023年3月の時点で、少なくとも因子分析に関しては統計学者でも満足のいく出力が得られるようになっていました。大変すばらしいことですね。
この調子で、そのうち【Pythonで統計モデル】第2弾SEM編も書いてみたいと思います。semopyが大変優秀だったので、ぜひSEMの分析がどこまでできるのか調べてみたいと思うようになりました。
この記事が気に入ったらサポートをしてみませんか?
