
【Pythonで統計モデル】因子分析2:探索的因子分析の実践
はじめに
株式会社GA technologiesの福中です。今、僕は、Advanced Innovation Strategy Center(以下AISC)という部署でChief Data Scientistとして働いています(詳しい自己紹介はAISC WEBサイトのプロフィールをご覧ください)。前回に引き続き、【Pythonで統計モデル】というシリーズの記事を書いていこうと思います。前回は、とりあえず簡単な1因子モデルを構築し、Pythonで探索的因子分析ができることを確認しました。
今回はそれをさらに発展させ、2因子以上の本格的な探索的因子分析においても、Pythonを使って実行可能であることを確認します。
注意点
本記事は統計学およびPythonの初心者向け解説記事ではありません。普段からR等を使って統計モデルによる分析や研究を行っている研究者の方が、改めてPythonで因子分析を行う必要が出た際のリファレンスとしての利用を想定しています。したがって、因子分析に不慣れな方は、先に以下で紹介するテキストをはじめとした初心者用の教科書で勉強するとよいと思います。
テキスト
本記事では東京図書から出版されている因子分析入門―Rで学ぶ最新データ解析―の分析結果を、Pythonを使って再現していきます。分析用データは東京図書のホームページからダウンロードできますので、興味のある方はぜひ試してみてください。
環境
本記事の分析は、OS: Windows 11、Python 3.11.2の環境下で行っています。また、必要なパッケージは以下となります。インストール済みの方は割愛してください。
# packageのインストール
pip install numpy pandas matplotlib japanize_matplotlib
pip install factor_analyzerなおPythonにおける因子分析のパッケージであるfactor_analyzerのドキュメントは以下となります。本記事ではここから重要な部分をいくつかピックアップしてご紹介します。網羅的な解説はしませんので、適宜、必要に応じてご参照ください。
多因子モデル
それでは、「第1章 速習・因子分析」の実践例として出てくる「スキー場データ」を例として探索的因子分析を行ってみましょう。このデータはC. E. Osgoodによって提唱されたSD(Semantic Differential)法を用いて測定された、24個のスキー場(コンセプト)に対する9個の形容詞対への評定結果です。各回答はすべて7件法によって測定されています。まずは以下のようにしてパッケージとデータの読み込みを行いましょう。
# packageの読み込み
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
from factor_analyzer import FactorAnalyzer# スキー場データの読み込み
df = pd.read_csv("dat/Ski.csv", encoding='shift_jis')
df_rowname = df.iloc[:, 0]
SDdat = df.iloc[:, 1:10]
SDdat.head()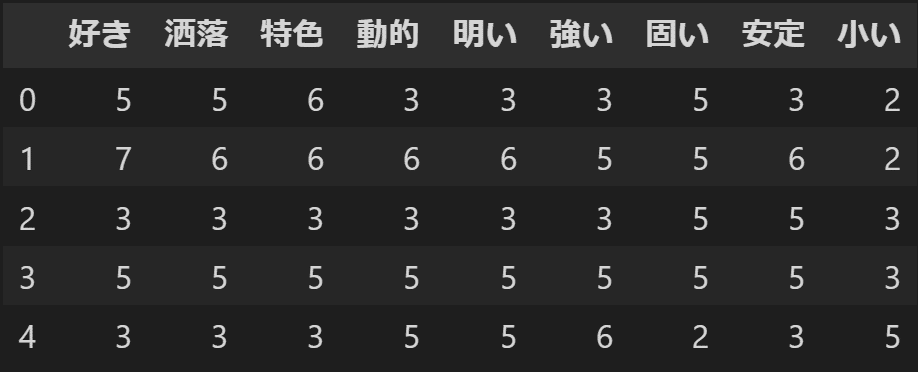
次に因子分析を行います。今回のデータはOsgoodのSD法を用いて測定されているので、まずは「評価」「活動性」「力量性」の3因子を仮定するのがよいと考えられます。そこで、因子数は3、回転法はプロマックス回転、母数推定には最尤法を設定します。Pythonのスクリプトは以下のようになります。
# 探索的因子分析の実行
fa = FactorAnalyzer(n_factors=3, rotation='promax', method='ml')
fa.fit(SDdat)分析の結果の因子負荷量を見てみましょう。
name = ["評価", "活動性", "力量性"]
loadings_df = pd.DataFrame(fa.loadings_, columns=name)
loadings_df.index = SDdat.columns
loadings_df["共通性"] = fa.get_communalities()
print(loadings_df) 評価 活動性 力量性 共通性
好き 0.942902 -0.004347 0.010143 0.889187
洒落 0.974212 0.054577 -0.008605 0.952142
特色 0.942451 -0.025292 -0.001663 0.888855
動的 0.033807 0.982529 0.022870 0.967029
明い 0.023925 0.915334 -0.039300 0.839953
強い -0.033451 0.930287 0.022516 0.867060
固い 0.000965 -0.136607 0.912502 0.851322
安定 0.089129 -0.040118 0.879204 0.782553
小い 0.092911 -0.159730 -0.974775 0.984332因子負荷量を見ると、見事に3因子の単純構造になっていることが見て取れます。また因子負荷量の値に関しては、テキストの値と小数点第2位で一致していることも確認できます。
次にスクリープロットを描いて、固有値の確認をしてみましょう。スクリプトは以下の通りです。
# スクリープロットを描く
eigen = fa.get_eigenvalues()
left = list(range(1, len(eigen[0])+1))
plt.plot(left, eigen[0], marker="o")
plt.ylabel("固有値")
ガットマン基準より、3因子モデルが妥当であることが見て取れます。また、因子間相関も確認しておきましょう。因子間相関はプロマックス回転など斜交回転を選択した場合にのみ出力できることに注意しましょう。
# 因子間相関の出力
phi = pd.DataFrame(fa.phi_, columns=name, index=name)
print(phi) 評価 活動性 力量性
評価 1.000000 0.286164 -0.141522
活動性 0.286164 1.000000 -0.317574
力量性 -0.141522 -0.317574 1.000000因子寄与、因子寄与率、累積寄与率も出力しておきましょう。これらは、get_factor_variance()というメソッドで算出することができます。スクリプトは以下となります。テキストと同様に、3つの因子で9個の観測変数の分散を89%説明できていることがわかります。
# 因子寄与(因子負荷量の二乗和)・因子寄与率・累積寄与率の出力
pd.DataFrame(fa.get_factor_variance(),
index=["因子寄与", "因子寄与率", "累積寄与率"],
columns=name) 評価 活動性 力量性
因子寄与 2.745779 2.718055 2.558599
因子寄与率 0.305087 0.302006 0.284289
累積寄与率 0.305087 0.607093 0.891381最後に因子得点を算出するスクリプトを書いておきます。
# 因子得点の算出
fa_score = pd.DataFrame(fa.transform(SDdat), columns=["評価", "活動性", "力量性"])
fa_score.index = df_rowname.rename("場所")
print(fa_score) 評価 活動性 力量性
場所
ニセコヒ 0.736712 -0.254410 0.460514
志賀高原 1.258831 1.469926 0.761850
万座温泉 -0.459288 -0.256888 0.406543
グランデ 0.648176 0.948251 0.427290
トマムリ -0.524176 1.105757 -1.063739
上越国際 1.278045 -0.768274 -1.257715
安比高原 1.168239 0.963040 0.659207
野沢温泉 -0.952460 -0.948936 0.730105
蔵王スキ -0.967702 -0.690441 0.989874
舞子後楽 1.340806 -0.881276 -1.480940
浦佐スキ -0.998049 -0.886986 1.590605
八方尾根 1.232474 -0.806361 1.035477
天神山ス 0.745102 1.056793 -0.772852
みつまた -1.027368 -0.371318 0.681715
猫魔スキ 1.175810 0.810610 -0.845649
五竜とお -1.011485 -1.231351 -1.182458
白馬スキ -0.643782 1.456298 -1.160122
栂池スキ -1.177201 1.669480 -1.452371
赤倉温泉 -0.927920 -0.255467 1.225085
妙高杉原 -0.915476 -0.764965 -1.126183
戸隠スキ -0.987807 -1.221041 0.749628
菅平スキ -0.963597 -0.800515 0.677384
猪苗代ス 0.714419 -0.819872 0.704882
軽井沢ス 1.257697 1.477946 -0.758132値を見るとテキストP.22の表1.12の因子スコアとは値が一致していませんが、テキストP.175の表7.8(Bartlettの方法による因子スコアの推定値)と小数点第2位の精度で一致していることが確認できます。このようにPythonを用いてもRなどと同じレベルで探索的因子分析を行うことができ、結果に関しても統計学者にとってほぼ満足のいく内容を出力させることができました。
それでは次回の因子分析3では、いよいよ本格的な分析に入っていきたいと思います。因子分析が良く使われるシチュエーションの1つが、心理学分野における尺度構成です。テキストの第2章では、この尺度構成を例にとって因子分析が利用されていますので、その内容をPythonで再現していきたいと思います。
この記事が気に入ったらサポートをしてみませんか?
