8-7 対応差の検定～対応のある２標本の母平均の差のｔ検定を様々な方法で実施

ネイピア DS

2023年9月6日 11:39

今回の統計トピック

統計的仮説検定のトピック「対応のある２標本の母平均の差の$${t}$$検定」を深掘りします。

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

問題を解いて、知る・実践する

今回の記事の構成

この記事は、通常の記事構成と違う章立てにいたします。
「問題を解く」「知る」「実践する」を１つの章にまとめます。
対応のある２標本の母平均の差の$${t}$$検定の一連の流れを、手作業・EXCEL・Pythonで実践いたします。

📘公式問題集のカテゴリ

検定の分野
問7 対応の差の検定（血圧の変化）

試験実施年月
調査中

📕公式テキスト：4.4.2 対応のある２標本の場合（154ページ～）

問題

公式問題集をご参照ください。

解き方

題意
与えられた条件から、検定に用いる$${t}$$分布の自由度と棄却域を求めます。

【条件】
・処置前の標本と処置後の標本の大きさは各10です。
・検証したいことは、処置後に数値が上がっているかどうか、です。
・有意水準$${5\%}$$の片側検定です。

公式問題集の記述を改変

読み解き

条件から統計的仮説検定の主題を読み解きます。

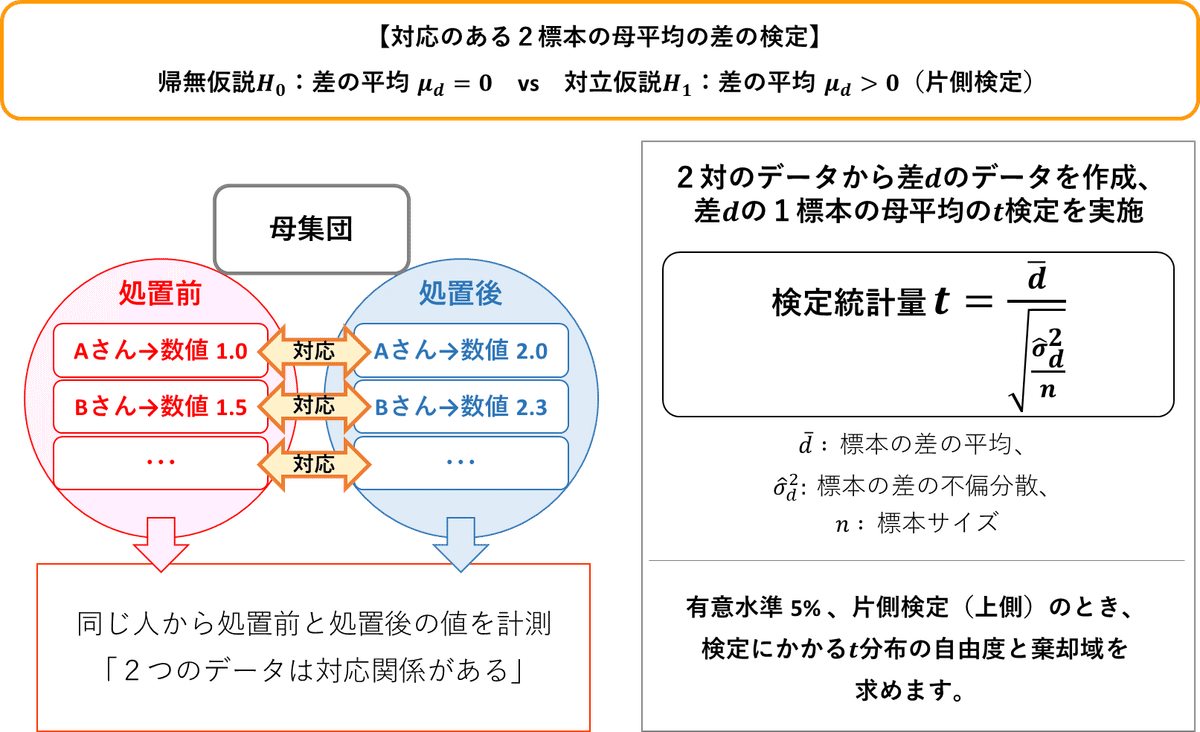
同一人物に対する処置前と処置後の２つの標本がNo.項目で「対応して」おり、「$${t}$$分布」を用いるので、「対応のある２標本の母平均の差の$${t}$$検定」です。
検定統計量は$${t}$$です。
対応する処置後の値と処置前の値の差を確率変数$${d}$$、$${d}$$の平均を$${\mu_d}$$、分散を$${\sigma^2_d}$$と置きます。
帰無仮説$${H_0}$$は「差の平均$${\mu_d=0}$$」（処置前後に差は無い）です。
対立仮説$${H_1}$$は「差の平均$${\mu_d>0}$$」（処置前後の差は0超、処置後に数値が上がっている）です。

この問題の統計的仮説検定の概要を図示します。

統計的仮説検定の手段

今回は、①手計算、②EXCEL、③Python の３つの手段で検定を実施いたします。

手計算で検定

問題では$${t}$$値や帰無仮説を棄却できるかどうかを出題していませんが、ひとまず、対応する２標本の平均の差の検定統計量$${t}$$から話を進めます。

■ 検定統計量$${\boldsymbol{t}}$$
帰無仮説が正しいと仮定するときの検定統計量 $${t}$$ を計算します。
計算結果の値を「$${t}$$値」と呼びます。
この問題で「帰無仮説が正しいと仮定する」とは、「差の平均$${\mu_d=0}$$である」と仮定することです。

検定統計量$${t}$$の計算式は次のとおりです。
なお、この検定統計量$${t}$$は自由度$${n-1}$$の$${t}$$分布に従います。

■公式　検定統計量$${t}$$（対応のある２標本の母平均の差編）
$${t=\cfrac{\bar{d}}{\sqrt{\frac{\hat{\sigma}^2_d}{n}}} \sim t(n-1)}$$

対応のある２標本の差を取って作成したデータは「１標本」です。
つまり、対応のある２標本の母平均の差の検定は「１標本の母平均の$${t}$$検定」に行き着くのです。

■ 問題に戻ります。
出題の「検定統計量$${t}$$が従う$${t}$$分布の自由度」と「棄却域」を検討します。

$${t}$$分布の自由度は、標本サイズ$${n-1}$$です。
この問題の標本サイズは$${10}$$ですので、自由度は$${10-1=9}$$です。

解答の１つ目は、自由度$${9}$$です。

棄却域の検討に移ります。
出題条件より、有意水準$${5\%}$$の片側検定ですので、$${t}$$分布のパーセント点表から、$${5\%}$$の上側確率パーセント点を取得します。

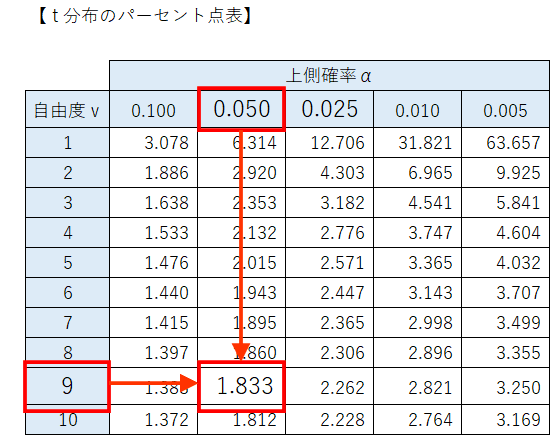
自由度$${9}$$の$${5\%}$$上側確率パーセント点は$${1.833}$$です。

対立仮説は処置後に数値が上がることを示す「差$${d>0}$$」です。
不等号の向きに注目しましょう。
$${t}$$値が上側確率パーセント点以上のときに帰無仮説を棄却することとなります。
式にすると、$${t\geq1.833}$$です。
グラフにすると「赤い点線の右側（上側）」になります。

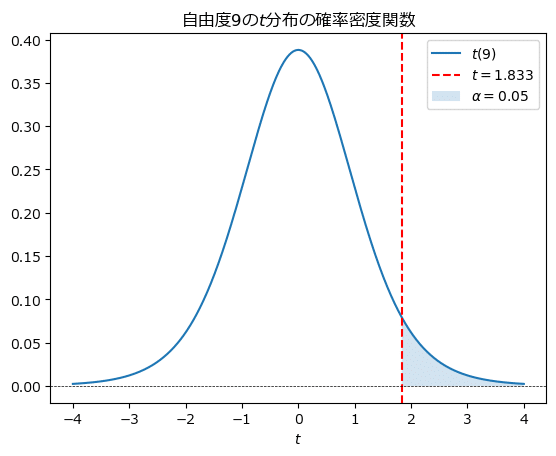
解答の２つ目は、棄却域$${t\geq1.833}$$です。

手計算は以上となります。

■ 最後まで統計的仮説検定を進める

出題範囲を超えていますが、統計的仮説検定を続けましょう！

まず$${t}$$値を求めます。
計算に必要な値は以下のとおりです。
・標本の差の平均$${\bar{d}}$$は$${4}$$です。
・標本の差の不偏分散$${\hat{\sigma}^2_d}$$は$${12}$$です。
・標本の差データの標本サイズは$${10}$$です。

検定統計量$t$の公式に当てはめます。

$$
\begin{align*}
t&=\cfrac{\bar{d}}{\sqrt{\frac{\hat{\sigma}^2_d}{n}}} \\
\\
&=\cfrac{4}{\sqrt{\cfrac{12}{10}}} \\
\\
&=3.6514 \cdots \\
&\fallingdotseq 3.651
\end{align*}
$$

$${t}$$値は$${3.651}$$です。

続いて帰無仮説を棄却できるかどうか確認しましょう。

計算した$${t}$$値は棄却域$${t>1.833}$$に該当します。
よって、有意水準$${\boldsymbol{5\%}}$$で帰無仮説は棄却され、対立仮説「処置後に数値が上がる」と言えます。

以上です。

EXCELで検定

EXCELで対応のある２標本の母平均の差の$${t}$$検定を行います。
①計算シートを利用する方法と、②分析ツール機能を利用する方法を紹介いたします。

①計算シートを利用

計算シートの全体像です。
【データ】エリアに対応のある２つの標本データを登録します。
そしてパラメータに有意水準と検定方法を入力します。

このシートは、T.TEST 関数を除いて、特別な関数を利用していません。
検定統計量$${t}$$の公式どおりに計算式を設定しており、$${t}$$値の上側確率は$${t}$$分布の関数 T.DIST.RT 関数を利用しています。

■統計的仮説検定の実行

シートのデータエリアに予め標本データをセットしています。
このデータとパラメータから$${t}$$値、$${p}$$値を自動計算します。
有意水準$${5\%}$$、片側検定（上側）で実行しましょう。

$${t}$$値$${=3.6515}$$、$${p}$$値$${0.0027}$$になりました。
$${p}$$値が有意水準$${5\%}$$を下回っており、帰無仮説は棄却されます。

■ T.TEST 関数

EXCELには「２標本の母平均の差の$${t}$$検定」の$${p}$$値を計算できる「 T.TEST 関数」があります。
便利です。
「②検定の種類」で「1：対応あり」を指定します。

②分析ツールを利用

EXCELの「分析ツール」には、次のような$${t}$$検定の分析表を作成する機能があります。
基本統計量、$${t}$$値、$${p}$$値、$${t}$$境界値が整然と表示されます。
簡単な操作で綺麗な分析表を得られるので、使い勝手がよさそうです！

■ 分散ツールの利用方法

１．データ分析メニュー

予め２つの標本データをEXCELに入力しておきます。
メニューより、「データ」（①）＞「データ分析」（②）を選択します。
「データ分析」画面が表示されます。

２．「データ分析」画面

対応のある２標本の母平均の差の$${t}$$検定を行う場合には、「ｔ検定：一対の標本による平均の検定」（③）を選択して、「ＯＫボタン」（④）をクリックします。
「ｔ検定：一対の標本による平均の検定」画面が表示されます。

３．「ｔ検定：一対の標本による平均の検定」画面

変数１の入力範囲（⑤）、変数２の入力範囲（⑥）に、２つの標本データの範囲を設定します。
出力オプションで分析表の出力先を指定します。
今回は、データのすぐ横のセル（⑦）を指定しました。
αに有意水準を指定します（⑧）。
今回は$${5\%=0.05}$$を設定します。

最後に「ＯＫボタン」（⑨）をクリックします。

４．分析表の表示

「出力先」で指定した場所に分析表が表示されました。

おっと忘れるところでした。

解答の自由度は$${9}$$、棄却域は$${t\geq1.833}$$です。
分析データの赤枠「自由度」と「t境界値片側」をご確認くださいませ。

また、片側$${p}$$値は「P(T<=t)片側」欄の$${0.0026}$$であり、有意水準$${5\%}$$よりも小さいので、帰無仮説は棄却されます。

EXCELは以上となります。

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

Pythonで検定

Pythonで対応のある２標本の母平均の差の$${t}$$検定を行います。
今回は、４種類の方法で検定しちゃいます！

インポート

import numpy as np
import pandas as pd

from scipy import stats
import pingouin as pg

import matplotlib.pyplot as plt

データの準備
３つのデータを準備します。

処置前データ：data_before
処置後データ：data_after
処置後と処置前の差データ：data_delta

# データ入力
data_before = np.array([130, 118, 128, 135, 126, 120, 126, 140, 127, 130])
data_after = np.array([135, 120, 132, 135, 129, 128, 135, 139, 135, 132])
data_delta = data_after - data_before

データの基本統計量とプロット
処置前・後・差の各データの概要を確認します。

# 基本統計量の表示（pandasデータフレーム利用）
data_merge = pd.DataFrame(
             {'処置前': data_before, '処置後': data_after, '差': data_delta})
data_merge.describe()

data_merge.plot()
plt.axhline(0, lw=0.5, ls='--', color='black')
plt.xlabel('ID')
plt.ylabel('値')
plt.show()

自由度と棄却域の算出
出題された自由度と棄却域を算出します。

# 検定統計量tが従うt分布の自由度と有意水準5%片側検定（上側）の棄却域

# パラメータ
alpha = 0.05             # 有意水準α
n = data_delta.shape[0]  # 標本サイズn
df = n - 1               # 自由度df

# 棄却限界値（上側パーセント点）の算出・表示
print(f'自由度 ＝ {df},  棄却域 t ≧ {stats.t.ppf(1-alpha, df=df):.3f}')

解答の自由度は$${9}$$、棄却域は$${t \geq 1.833}$$です。

では引き続き、検定を実施しましょう。

① scipy.statsのttest_rel利用（対応のある２標本の母平均の差のt検定）
対応のある２標本の母平均の$${t}$$検定の機能です。
「処置前・後のデータ」を用います。

# 対応のある２標本の母平均の差のt検定 片側検定（上側）
t_value, p_value = stats.ttest_rel(
                         data_after,            # 処置後データ
                         data_before,           # 処置前データ
                         alternative='greater') # 片側検定（上側）

print(f't値: {t_value:.3f}, p値: {p_value:.3f}')

② scipy.statsのttest_1samp利用（１標本の母平均のt検定）
１標本の母平均の$${t}$$検定の機能です。
「差データ」を用います。

# 母平均の差のt検定（１標本）　片側検定（上側）
t_value, p_value = stats.ttest_1samp(
                         data_delta,            # 差データ
                         popmean=0,             # 帰無仮説の母平均=0
                         alternative='greater') # 片側検定（上側）

print(f't値: {t_value:.3f}, p値: {p_value:.3f}')

③ pingouinのttest利用（t検定）
$${t}$$検定全般の機能です。
「処置前・後のデータ」を用います。

# 対応のある２標本の母平均の差のt検定 片側検定（上側）
pg.ttest(
         data_after,            # 処置後データ
         data_before,           # 処置前データ
         paired=True,           # 対応のある２標本
         alternative='greater', # 片側検定（上側）
         correction=False       # スチューデントのt検定
        ).round(3)

④ 検定統計量tの公式どおりに計算
１標本の母平均の$${t}$$検定（片側検定・上側）の計算を手組みしました。
「差データ」を用います。

# 母平均の差のt検定（１標本）　片側検定（上側）
# 検定統計量tの公式どおりに計算、t分布よりp値を取得

# 設定 帰無仮説:差の母平均は0
mu = 0

# 検定統計量tの算出に利用するデータ
num_delta = data_delta.shape[0]            # 差データの標本サイズ
delta_mean = data_delta.mean()             # 差データの平均
delta_sigma2_hat = data_delta.var(ddof=1)  # 差データの不偏分散

# t値の算出
t_value = (delta_mean - mu) / np.sqrt(delta_sigma2_hat/ num_delta)

# p値の算出
p_value = stats.t.sf(t_value, df=num_delta-1)

print(f't値: {t_value:.3f}, p値: {p_value:.3f}')

まとめますと、$${t}$$値は$${3.651}$$、$${p}$$値は$${0.003}$$です。
$${p}$$値は$${0.003}$$であり、有意水準$${5\%}$$よりも小さいので、帰無仮説は棄却されます。

また、対応のある２つの標本データを用いた「対応のある２標本の母平均の差の$${t}$$検定」と、２つの標本の差データを用いた「１標本の母平均の$${t}$$検定」は、$${t}$$値、$${p}$$値が同じ結果になることが分かりました。

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

以上で終了です。
お疲れ様でした。

解答

① です。

難易度　やさしい

・知識：対応のある２標本の母平均の差の$${t}$$検定、$${t}$$分布のパーセント点表
・計算力：不要
・時間目安：1分

おわりに

対応のある２標本の母平均の差の$${t}$$検定も、対応のない２標本の母平均の差の検定と同様に、EXCELもPython も専用機能が整っており、サクッと計算できます。
お手元に対応する２つのデータがありましたら、平均値に差があるかどうかを調べてみましょう。
EXCEL や Python でサクッと！

最後までお読みいただきまして、ありがとうございました。

のんびり統計シリーズの記事

次の記事

前の記事

この記事が参加している募集

夏の思い出

26,180件

この記事が気に入ったらサポートをしてみませんか？