
6-5 t分布の確率計算 ~ 正規分布・標本分布・t分布の旅(実験あります)
今回の統計トピック
$${t}$$分布を掘り下げます。
$${t}$$分布はスチューデントの$${t}$$分布とも呼ばれます。
標本分布と$${t}$$分布の関係に迫ります!
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
標本分布の分野
問5 $${t}$$分布の確率計算(データなし)
試験実施年月
調査中(類似問題:統計検定2級 2019年6月 問12(回答番号21)
問題
公式問題集をご参照ください。
解き方
題意
「正規分布に従う母集団から無作為抽出した標本」が従う分布に関する問題です。
次の母集団と標本について考えます。
・母集団は平均$${\mu}$$、分散$${\sigma^2}$$の正規分布に従います。
・母集団からランダムに標本サイズ$${9}$$の標本を抽出します。
・標本平均を$${\bar{X}}$$、標本不偏分散を$${S^2}$$とします。
次の過程を追って、$${P(\bar{X} \geq \mu + 0.62S)}$$の値を求めます。
・$${T=\cfrac{\bar{X}-\mu}{\sqrt{S^2/9}}}$$の従う分布を考えます。
・$${P(\bar{X} \geq \mu + 0.62S)=P \left(T\geq\cfrac{0.62S}{\sqrt{S^2/9}} \right)=P(T\geq1.86)}$$から確率の値を求めます。
$${\boldsymbol{t}}$$分布
公式テキストの$${t}$$分布の項の記述を参考にして、「正規分布に従う母集団から無作為抽出した標本から得られる統計量$${t}$$」をまとめました。
正規分布$${N(\mu, \sigma^2)}$$に従う母集団から無作為抽出した大きさ$${n}$$の標本に関して、$${t=\cfrac{\bar{X}-\mu}{\sqrt{S^2/n}}}$$は自由度$${n-1}$$の$${t}$$分布に従います。
$${\bar{X}}$$は標本平均、$${S^2}$$は不偏分散です。
この$${t}$$分布の記述を踏まえると、問題文の$${T=\cfrac{\bar{X}-\mu}{\sqrt{S^2/9}}}$$が従う分布は、標本サイズ$${n=9}$$なので、自由度$${8 \quad (n-1=9-1=8)}$$の$${t}$$分布です。
解答は(ア)(自由度)$${8}$$、(イ)$${t}$$(分布)です。
$${\boldsymbol{t}}$$分布のパーセント点表
問題文によって、$${P(T\geq1.86)}$$が明らかにされています。
$${t}$$分布の確率は「$${t}$$分布のパーセント点表」で取得できます。
この表で、自由度$${8}$$の$${t}$$分布のパーセント点$${1.86}$$に対する上側確率$${\alpha}$$を探します。

自由度$${8}$$の行に$${1.860}$$を見つけました。
表の上部に視線を移しましょう。
上側確率$${\alpha}$$は$${0.05}$$です。
解答は(ウ)(確率の値は)$${0.05}$$です。
解答
③ (ア)8、(イ)t、(ウ)0.0500 です。
難易度 やさしい
・知識:標本平均の分布、$${t}$$分布、$${t}$$分布のパーセント点表
・計算力:数式読解(低)
・時間目安:1分
知る
おしながき
公式問題集の問題に接近してみましょう!
今回は、$${\boldsymbol{t}}$$分布のイメージに接近しましょう。
その前に、確率分布を掘り下げる意味合いについて、少し考えてみましょう。
確率分布で何かできるの?
確率分布を活用することによって、統計的に推定をしたり、仮説検定を行ったりできます。
特に、一部のデータを調べて全体像を理解する際に活躍します。
母集団と呼ばれる全体像から一部を適切に抽出します。これが標本です。
この標本を調べて、推定や仮説検定を行うのです。

統計的区間推定(雰囲気レベル)
区間推定のテーマでは、例えば、母集団の平均。
標本調査を実施して得られた統計量に基づき、「95%信頼区間で平均の値は$${52 \pm 5}$$」のように、信頼区間を設定して区間の幅をもたせて推定を行います。
そして信頼区間の「95%」に確率分布を用いています!
例えば正規分布の確率。
次のグラフの青い領域=確率95%を活用して、信頼区間の計算をします。

統計的仮説検定(雰囲気レベル)
統計的仮説検定のテーマでは「めったに起きないことが起きた」という判断基準で確率分布を活用します。
例えば「コインの表と裏が出る割合は等しく1/2」という仮説を立てて、コイントスを20回試行したところ、全て表が出たとします。
めったに起きないことが起きた感じがしますね!

統計的仮説検定では「有意水準5%でコインの表が出る割合1/2という仮説を棄却します」というように、有意水準◯%という「しきい値」を設定して、仮説検定を行います。
そして有意水準の「5%」に確率分布を用いています!
ここでも例えば正規分布の確率。
次のグラフの両端の青い領域=確率5%を活用して、有意水準と比べてどうか(棄却域に入るか)を計算します。

正規分布を想定する
統計検定2級では、主に「正規分布」を想定する問題が出題されます。
標準正規分布を利用したり、正規分布を背景に持つ別の確率分布を利用したり。
$${\boldsymbol{t}}$$分布も正規分布を背景に持つ確率分布なのです。
確率の表を活用する
そして、統計検定©の特徴として、確率の具体的な値を「付属の表」(紙)から取得することが挙げられます。
正規分布の例では、「標準正規分布の上側確率表」を用います。
上側確率表を利用するための前処理として、確率変数の標準化をします。
こんな感じです。

そうすると、「標準正規分布の上側確率表」で確率を見つけることができます。
次の図の例では、確率変数を標準化して得た$${z}$$値$${=1.00}$$を用いて、確率$${0.1587}$$を取得しています。


将来的には、統計検定の解答作業で確率の表を用いることが無くなって、コンピュータを活用して確率を求められるようになるといいですね。
それでは$${t}$$分布に話を移しましょう。
t分布
📕公式テキスト:2.10.2 $${t}$$分布(89ページ~)
まずは$${t}$$分布のグラフを見ましょう。

$${0}$$を境にして左右対称の形状です。
パラメータは自由度です。この図では$${\nu}$$です。
自由度の値が大きくなるにつれて、峰の形状が尖り、両端(裾)が薄くなり、赤い線の標準正規分布に近づきます。
なんとなく・・・、正規分布と関係がありそうですね!匂います!
正規分布と$${\boldsymbol{\chi^2}}$$分布と$${\boldsymbol{t}}$$分布
$${t}$$分布の定義です。
$${t}$$分布に関する公式テキストの記述を改変しました。
2つの独立な確率変数$${Z}$$と$${W}$$について、$${Z}$$が標準正規分布$${N(0,1)}$$に従い、$${W}$$が自由度$${m}$$の$${\chi^2}$$分布に従うとき、確率変数$${t=\cfrac{Z}{\sqrt{W/m}}}$$が従う分布を自由度$${m}$$の$${t}$$分布と呼び、$${t(m)}$$と表します。
$${t}$$分布は、「標準正規分布に従う確率変数$${Z}$$」と「自由度$${m}$$の$${\chi^2}$$分布に従う確率変数$${W}$$」を用いて示された、「確率変数$${t}$$の従う分布」です。
ちなみに、$${\chi^2}$$分布も正規分布と関係が強いです。
互いに独立に標準正規分布$${N(0, 1)}$$に従う確率変数$${Z_1, Z_2, \cdots, Z_n}$$について、$${W=Z^2_1+Z^2_2+\cdots +Z^2_n}$$の従う分布を自由度$${n}$$の$${\chi^2}$$分布と呼び、$${\chi^2(n)}$$と表します。
つまり、$${t}$$分布は幾つもの正規分布に従う確率変数によって成り立っているのです。
正規分布の生命力の強さを感じます。

標本分布と$${\boldsymbol{t}}$$分布
さらに$${t}$$分布は、「正規分布に従う母集団」より抽出した標本から得られる統計量(標本平均など)が従う標本分布なのです。

文章にするとこんな感じです。公式テキストを参考にしました。
正規分布$${N(\mu, \sigma^2)}$$に従う母集団から無作為抽出した標本$${X_1, X_2, \cdots, X_n}$$について、標本平均$${\bar{X}=\sum^n_{i=1}X_i/n}$$、標本不偏分散$${S^2=\sum^n_{i=1}(X_i-\bar{X})/(n-1)}$$とするとき、確率変数$${t=\cfrac{\bar{X}-\mu}{S/\sqrt{n}}}$$は自由度$${n-1}$$の$${t}$$分布、$${t(n-1)}$$に従います。
Pythonで実験
正規母集団から標本を無作為抽出して求めた$${t}$$の実現値が$${t}$$分布に従うのか、Pythonで実験してみましょう!
平均$${0}$$、分散$${1}$$の標準正規分布に従う乱数を$${5}$$個($${n=5}$$)取得して、$${t=\cfrac{\bar{X}-\mu}{S/\sqrt{n}}}$$の計算式で$${t}$$の実現値を計算します。
この計算を10000回繰り返し実行してヒストグラム(青色)にしました。
オレンジの線は自由度$${4}$$の$${t}$$分布の確率密度関数(理論値)です。
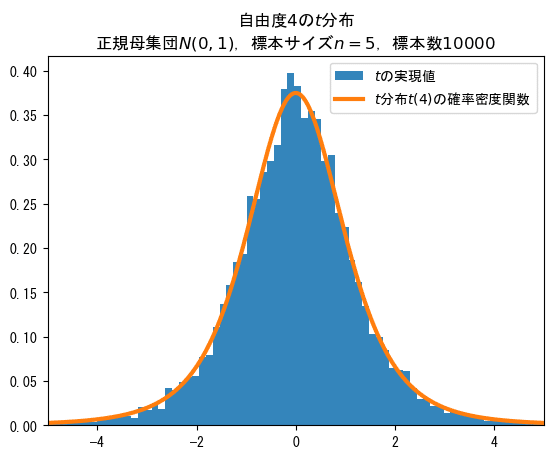
ほぼ一致していますね!
$${n}$$個の標本から求めた$${t}$$の値は自由度$${n-1}$$の$${t}$$分布に従うことを視覚的に確認できました!やったね!
では公式問題集の問題に戻って、確率変数$${t}$$に変換しましょう。
確率変数$${\boldsymbol{t}}$$の変換
公式問題集の問題を思い出します。
次の過程を追って、$${P(\bar{X} \geq \mu + 0.62S)}$$の値を求めます。
・$${T=\cfrac{\bar{X}-\mu}{\sqrt{S^2/9}}}$$の従う分布を考えます。
・$${P(\bar{X} \geq \mu + 0.62S)=P \left(T\geq\cfrac{0.62S}{\sqrt{S^2/9}} \right)=P(T\geq1.86)}$$から確率の値を求めます。
確率変数$${T=\cfrac{\bar{X}-\mu}{\sqrt{S^2/9}}}$$は自由度$${8}$$の$${t}$$分布、$${t(8)}$$に従います。
$${P(\bar{X} \geq \mu + 0.62S)}$$を確率変数$${T}$$で置き換えていきましょう。
$${\mu}$$は母平均、$${\bar{X}}$$は標本平均、$${S^2}$$は標本不偏分散、標本サイズ$${n=9}$$です。
では、変換&計算開始です!

$$
\begin{align*}
P(\bar{X} \geq \mu + 0.62S)&=P \left( \cfrac{\bar{X} -\mu}{\sqrt{S^2/9}} \geq \cfrac{\mu+0.62S-\mu}{\sqrt{S^2/9}} \right)\\
\\
&=P \left( T \geq \cfrac{0.62S}{\sqrt{S^2/9}} \right)\\
\\
&=P \left( T \geq \cfrac{0.62S}{\sqrt{(S/3)^2}} \right)\\
\\
&=P \left( T \geq \cfrac{0.62S}{S/3} \right)\\
\\
&=P \left( T \geq \cfrac{0.62}{1/3} \right)\\
\\
&=P \left( T \geq 0.62 \times 3 \right)\\
&=P \left( T \geq 1.86 \right)\\
\end{align*}
$$
公式問題集の問題の通り、$${P(\bar{X} \geq \mu + 0.62S)=P( T \geq 1.86 )}$$を導くことができました。
確率変数$${T}$$は自由度$${8}$$の$${t}$$分布に従います。
$${\boldsymbol{t}}$$分布のパーセント点表
自由度$${8}$$の$${t}$$分布に従う確率変数$${T}$$について、$${P( T \geq 1.86 )}$$の意味は、パーセント点$${t_\alpha(8)=1.86}$$を基準にした自由度$${8}$$の$${t}$$分布の上側確率です。
次のグラフの青い領域の面積が上側確率です。

では、$${t}$$分布のパーセント点表を見てみましょう。
行に「自由度$${\nu}$$」、列に上側確率$${\alpha}$$単位で「パーセント点$${t_{\alpha}(\nu)}$$」を配置する表です。

自由度$${8}$$の行にパーセント点$${1.860}$$を見つけました。
このパーセント点の上側確率が$${0.050}$$です。
つまり、確率$${P( T \geq 1.86)=0.050 }$$です。
まとめ
確率・推定・仮説検定などに取り組む際に、「母集団が正規分布に従っていて」、「標本不偏分散($${S^2}$$や$${\hat{\sigma}^2}$$などの記号)を用いるとき」には、自由度$${n-1}$$の$${t}$$分布と確率変数$${t=\cfrac{\bar{X}-\mu}{S/\sqrt{n}}}$$に思いを馳せてみましょう。

長旅、お疲れ様でした。
正規分布、$${t}$$分布を身近に感じていただけたなら幸いです🍀
実践する
t分布のグラフを描画してみよう
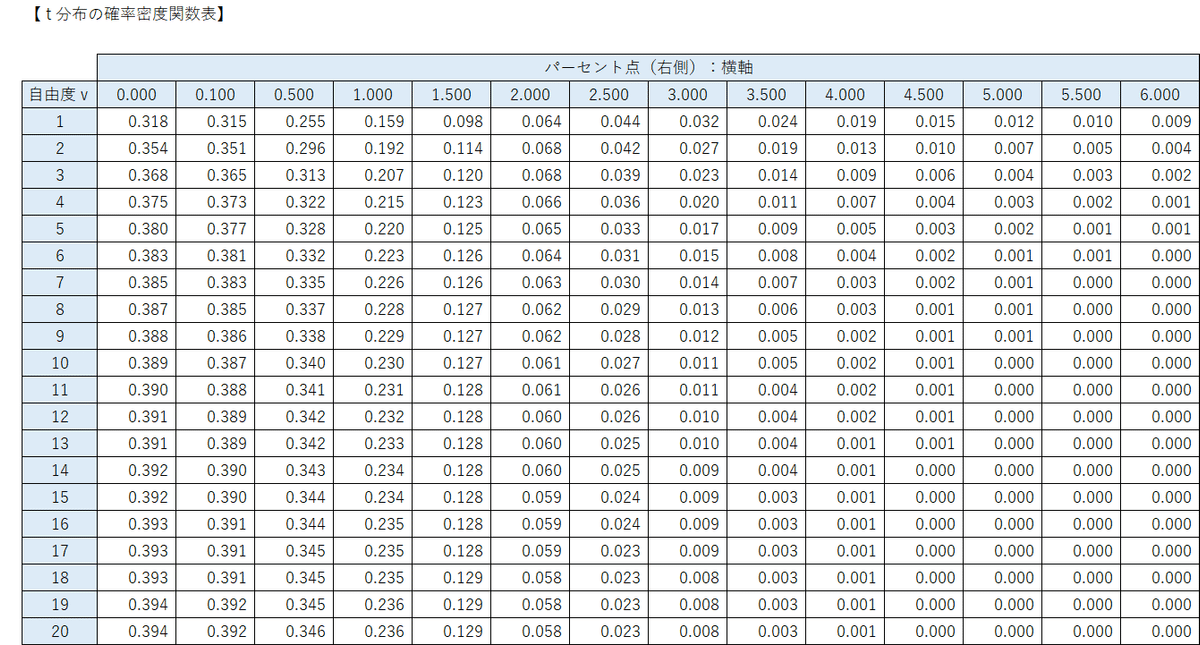
$${t}$$分布の確率密度関数をグラフに描いてみましょう!
次の「$${t}$$分布の確率密度関数表」を用いて、$${t}$$分布の確率をグラフに起こすのです。
EXCELファイルのダウンロード
こちらのリンクから「$${t}$$分布の上パーセント点表」と「$${t}$$分布の確率密度関数表」のEXCELファイルをダウンロードできます。

電卓・手作業で作成してみよう!
手作業で標準正規分布の確率密度関数のグラフを描いてみましょう!
一番記憶に残る方法ですし、試験本番の電卓作業のトレーニングにもなります。
「$${t}$$分布の確率密度関数表」を用いて$${t}$$分布の確率密度関数をグラフ化してみましょう。

0から6までのパーセント点は、グラフの横軸(x軸)の右側の値です。
パーセント点と自由度に囲まれた値が確率密度関数の値でありグラフの縦軸(y軸)の値になります。
例えば、行「自由度1」列「パーセント点0」の「値0.318」は自由度$${1}$$の$${t}$$分布のパーセント点$${0}$$のときの確率密度関数の値です。
EXCELで作成してみよう!
データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。
$${\boldsymbol{t}}$$分布のグラフの作成
$${t}$$分布の確率密度関数の値は「T.DIST」関数で取得できます。
=T.DIST(xの値,自由度,FALSE:確率密度関数)
次のサンプルは、自由度 4 の$${t}$$分布について、 B6セルから始まる x の値 -100~10 に対して、C7セル以降で確率密度関数の値を計算しています。

EXCELサンプルファイルには、次のパターンの$${t}$$分布のグラフを表示しています。
「自由度」の値を変更して、さまざまな$${\boldsymbol{t}}$$分布の形状を確認してみましょう!
■自由度を1つ設定するパターン
■自由度を4つ設定するパターン

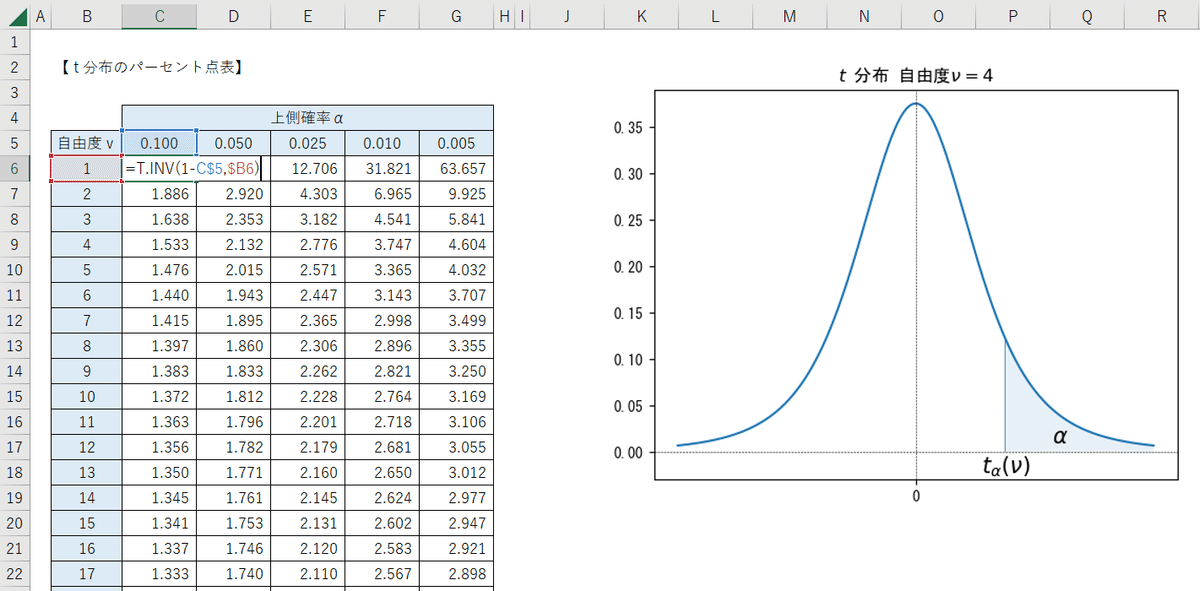
パーセント点表
「$${t}$$分布の上パーセント点表」では、「確率密度関数の値」と「自由度」からパーセント点を求める「T.INV関数」を利用しています。
=T.INV( 確率密度関数の値, 自由度 )
上側確率の欄には、$${t}$$分布の確率密度関数のグラフの青い領域=上側確率を表示しています。
一方で、パーセント表を作成するにあたって、T.INV関数の引数:確率密度関数の値には、グラフの白い領域=「下側確率」が必要になります。
そこで、引数に「1-上側確率」を設定しています。
EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
Pythonで作成してみよう!
プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。
今回は、$${\boldsymbol{t}}$$分布の可視化に取り組みます。
①インポート
scipy.statsの t を利用して、確率密度関数、累積分布関数、パーセント点を取得します。
import numpy as np
from scipy.stats import t, norm
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline②t分布の確率密度関数のプロット
パラメータに自由度を設定して、さまざまなt分布の確率密度関数を可視化しましょう。
t.pdf(xデータ, 自由度)でt分布の確率密度関数の値を取得します。
■自由度3.8の単グラフ
# 【設定】t分布のパラメータ「自由度」を ,で繋いで指定
params = [3.8]
# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = -5, 5
# 描画 t.pdf(x, 自由度)
x = np.linspace(x_min, x_max, 1000)
for df in params:
plt.plot(x, t.pdf(x, df), label=f'$t({df})$')
plt.title('$t$分布 確率密度関数')
plt.legend()
# plt.savefig('./t_pdf1.png') # グラフ画像ファイルの保存
plt.show()
■自由度1,3,5,10の4グラフ
# 【設定】t分布のパラメータ「自由度」を ,で繋いで指定
params = [1, 3, 5, 10]
# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = -5, 5
# 描画 t.pdf(x, 自由度)
x = np.linspace(x_min, x_max, 1000)
for df in params:
plt.plot(x, t.pdf(x, df), label=f'$t({df})$')
plt.title('$t$分布 確率密度関数')
plt.legend()
# plt.savefig('./t_pdf2.png') # グラフ画像ファイルの保存
plt.show()
③t分布の累積分布関数のプロット
パラメータに自由度を設定して、さまざまなt分布の確率密度関数を可視化しましょう。
t.cdf(xデータ, 自由度)でt分布の累積分布関数の値を取得します。
■自由度3.8の単グラフ
# 【設定】t分布のパラメータ「自由度」を ,で繋いで指定
params = [3.8]
# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = -5, 5
# 描画 t.cdf(x, 自由度)
x = np.linspace(x_min, x_max, 1000)
for df in params:
plt.plot(x, t.cdf(x, df), label=f'$t({df})$')
plt.title('$t$分布 累積分布関数')
plt.legend()
# plt.savefig('./norm_cdf1.png') # グラフ画像ファイルの保存
plt.show()
■自由度1,3,5,10の4グラフ
# 【設定】t分布のパラメータ「自由度」を ,で繋いで指定
params = [1, 3, 5, 10]
# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = -5, 5
# 描画 t.cdf(x, 自由度)
x = np.linspace(x_min, x_max, 1000)
for df in params:
plt.plot(x, t.cdf(x, df), label=f'$t({df})$')
plt.title('$t$分布 累積分布関数')
plt.legend()
# plt.savefig('./norm_cdf1.png') # グラフ画像ファイルの保存
plt.show()
④t分布の確率いろいろ
■パーセント点を指定して上側確率を算出
まずは関数を定義します。
累積分布関数 t.cdf( パーセント点, 自由度 )を用いて下側確率を求めます。
1から下側確率を差し引いて上側確率を算出します。
def t_dist_upper(x_min, x_max, b, df):
# 確率密度関数の値の取得
x = np.linspace(x_min, x_max, 1001) # 確率変数 X の値を取得
y = t.pdf(x, df) # 確率密度関数f(x)の値を取得
# 確率の計算
prob = 1 - t.cdf(b, df) # bの上側確率を取得
# 描画区間の値の取得
y0 = 0 # y=0
x_draw = np.linspace(b, x_max, 1001) # 区間[b, x_max]の変数Xの値を取得
y_draw = t.pdf(x_draw, df) # 区間[b, x_max]の関数f(x)の値を取得
# 確率密度関数の描画
plt.plot(x, y) # 確率密度関数の描画
plt.fill_between(x_draw, y_draw, y0, # 区間[b, x_max]の塗りつぶし描画
alpha=0.1)
plt.hlines(y0, b, x_max, lw=0.5) # y=0の水平線の描画 b≦X≦x_max
plt.vlines(b, y0, y_draw[0], lw=0.5) # x=bの垂直線の描画
plt.hlines(y0, x_min, x_max, lw=0.5, # y=0の水平点線の描画 x_min≦X≦x_max
color='gray', ls='--')
plt.title(f'自由度${df}$の$t$分布 確率密度関数\n'
f'パーセント点{b}の上側確率 ${prob:.3f}$')
plt.tight_layout()
plt.show()この関数を実行する際には、自由度、上側確率を算出するパーセント点等を指定します。
確率$${P(t\geq1.5)}$$の$${1.5}$$のように、パーセント点が明らかになっていて確率を求める際に活用できます。
さまざまな自由度、パーセント点を試してみてください。
次の例では、パーセント点 2.262 を設定して実行しました。
上側確率は 0.025(2.5%)です。
# 【設定】t分布の自由度
df = 9
# 【設定】上側確率を算出するパーセント点b
b = 2.262
# 【設定】確率密度関数f(x)の描画区間[x_min,x_max]
x_min, x_max = -5, 5
# 処理の実行
t_dist_upper(x_min, x_max, b, df)
■両側確率を指定してパーセント点を算出
こちらも関数化しています。
t.ppf( 確率, 自由度 )を用いてパーセント点を求めます。
両側確率は上側確率と下側確率の両方を足した値なので、t.ppf の確率を 1/2 しています。
def t_dist_percent_bothside(x_min, x_max, p, df):
# 確率密度関数の値の取得
x = np.linspace(x_min, x_max, 1001) # 確率変数 X の値を取得
y = t.pdf(x, df) # 確率密度関数f(x)の値を取得
# 上側確率、下側確率のパーセント点の取得
pp_upp = t.ppf(1-p/2, df)
pp_low = t.ppf(p/2, df)
# 描画区間の値の取得
y0 = 0 # y=0
color = 'steelblue'
x_draw1 = np.linspace(x_min, pp_low, 1001) # 区間[x_min, pp_low]の変数Xの値を取得
y_draw1 = t.pdf(x_draw1, df) # 区間[x_min,pp_low]の関数f(x)の値を取得
x_draw2 = np.linspace(pp_upp, x_max, 1001) # 区間[pp_upp, x_max]の変数Xの値を取得
y_draw2 = t.pdf(x_draw2, df) # 区間[pp_upp, x_max]の関数f(x)の値を取得
# 確率密度関数の描画
plt.plot(x, y) # 確率密度関数の描画
plt.fill_between(x_draw1, y_draw1, y0, # 区間[x_min,pp_low]の塗りつぶし描画
color=color, alpha=0.1)
plt.fill_between(x_draw2, y_draw2, y0, # 区間[pp_upp, x_max]の塗りつぶし描画
color=color, alpha=0.1)
plt.hlines(y0, x_min, pp_low, lw=0.5) # y=0の水平線の描画 x_min≦X≦pp_low
plt.hlines(y0, pp_upp, x_max, lw=0.5) # y=0の水平線の描画 pp_upp≦X≦x_max
plt.vlines(pp_low, y0, y_draw1[-1], lw=0.5) # x=pp_lowの垂直線の描画
plt.vlines(pp_upp, y0, y_draw2[0], lw=0.5) # x=pp_uppの垂直線の描画
plt.hlines(y0, x_min, x_max, lw=0.5, # y=0の水平点線の描画 x_min≦X≦x_max
color='gray', ls='--')
plt.title(f'自由度${df}$の$t$分布 確率密度関数\n'
f'両側確率${p*100:.2f}\%$点: {pp_low:.4f}, {pp_upp:.4f}')
plt.tight_layout()
plt.show()自由度、両側確率等を指定して実行します
確率が判明していてパーセント点を求める際に活用できます。
さまざまな自由度、確率を試してみてください。
次の例では、両側確率 0.1 (10%)を設定して実行しました。
両側 10% 点は、下側確率 5% 点が -1.9432、上側確率 5% 点が 1.9432 です。
# 【設定】t分布の自由度
df = 6
# 【設定】両側確率
p = 0.1
# 【設定】確率密度関数f(x)の描画区間[x_min,x_max]
x_min, x_max = -5, 5
# 処理の実行
t_dist_percent_bothside(x_min, x_max, p, df)
⑤Pythonで実験!
標本の$${t}$$の値が$${t}$$分布に従うかどうかの実験です。
パラメータ(設定)は、標本サイズ n 、正規分布に従う母集団の母平均 mu と母標準偏差 stddev 、標本数(繰り返し処理数) num_samples です。
パラメータを変更して、実験してみてくださいね!
# 設定
n = 5 # 標本サイズn
mu, stddev = 0, 1 # 正規母集団の母平均mu、母標準偏差stddev
num_samples = 10000 # 標本数(n個の標本を採取する回数)
# 初期値設定
np.random.seed(1)
t_list = []
# 正規分布乱数で生成した標本xからtの実現値を算出
for i in range(num_samples):
x = norm.rvs(mu, stddev, size=n) # N(mu, stddev^2)の標本x
x_bar = np.mean(x) # 標本平均x_bar
nbvar = np.var(x, ddof=1) # 標本不偏分散nbvar
t_val = (x_bar - mu) / np.sqrt(nbvar / n) # tの実現値
t_list.append(t_val)
# t分布の確率密度関数を取得
x = np.linspace(-5, 5, 1001)
y = t.pdf(x, df=n-1)
# プロット
# 標本より取得したtの実現値ヒストグラムのプロット
plt.hist(t_list, bins='auto', density=True, alpha=0.9, label='$t$の実現値')
# t分布の確率密度関数のプロット
plt.plot(x, y, lw=3, label=f'$t$分布$ t({n-1})$の確率密度関数')
plt.title(f'自由度${n-1}$の$t$分布\n'
f'正規母集団$N({mu}, {stddev**2})$, 標本サイズ$n={n}$, '
f'標本数${num_samples}$')
plt.xlim(-5, 5)
plt.legend()
plt.show()
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
今回も楽しく$${t}$$分布を掘り下げることができました。
正規分布と標本と$${t}$$分布のつながりが、今後のテーマになる「統計的推定」「統計的仮説検定」に発展します。
この記事を将来の推定・検定に結実できるように読んでいただけたなら、嬉しいです。
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
この記事が気に入ったらサポートをしてみませんか?
