
「スモールデータ解析と機械学習」を寄り道写経 ~ 第6章「異常検知問題」
第6章「異常検知問題」
書籍の著者 藤原幸一 先生
この記事は、テキスト「スモールデータ解析と機械学習」第6章「異常検知問題」の通称「寄り道写経」を取り扱います。
今回は様々な異常検知アルゴリズムに挑戦します!
ではテキストを開いてスモールデータの旅に出発です🚀
このシリーズは書籍「スモールデータ解析と機械学習」(オーム社、「テキスト」と呼びます)の機械学習の理論・数式とPythonプログラムを参考にしながら、テキストにはプログラムの紹介が無いけれども気になったテーマ、または、テキストのプログラム以外の方法を試したいテーマを「実験的」にPythonコード化する寄り道写経ドキュメンタリーです。
はじめに
テキスト「スモールデータ解析と機械学習」のご紹介
テキストは、2022年2月に発売され、スモールデータと呼ばれる小さなサンプルサイズのデータを用いた機械学習の取り組み方について、理論(数式)とPythonサンプルプログラムを提案する素晴らしい実用書です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「スモールデータ解析と機械学習」第1版第1刷、著者 藤原幸一、オーム社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
第6章 異常検知問題
主に Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
この記事はおそらくスモールデータの寄り道写経史上、最大のコード量になる予定です!
おおまかには、①6.1節「局所外れ値因子法(LOF)」から6.6節「時系列データの取り扱い」を一層楽しむためのサンプルコードと、②6.8節「Tennessee Eastmanプロセス」以降の誤植+αコードに取り組みます。
異常検知タスクに取り組むのはほぼほぼ初めてなので、気合が入っています🦾🦾🦾

テキストの6.1節~6.6節ではとても興味深いアルゴリズムが多数紹介されています。
しかし6.1節~6.6節の中では各アルゴリズムを動かすコードの紹介がありません、残念です。。。
「でもでもプログラムを動かしてアルゴリズムを体感したい」
読み進めるにつれて、こんな欲が芽生えて、大きくなっていきました。
自分自身の満足を目的にしてサンプルコードを作成しました!
この章の寄り道ポイントです。
1.座学中心のテーマに関するPythonコードの実装
・6.1節「局所外れ値因子法(LOF)」(scikit-learn使用)
・6.2節「アイソレーションフォレスト」(scikit-learn使用)
・6.3節「多変量統計的プロセス管理(MSPC)」
・テキストのMSPC関数使用
・6.5節「管理限界の調整」にも言及
・6.6節「時系列データの取り扱い」(テキストのMSPC関数使用)
2.6.8節「Tennessee Eastmanプロセスの異常検知」
異常データ IDV1 を対象にして、以下の点に関するテキストオリジナルコードのアップデートを試みます。
・誤植およびエラーの回避策
・異常検知結果プロットの関数化
・寄与プロットをトップ5表示に改造

6.1 局所外れ値因子法(LOF)
局所外れ値因子法(LOF)はサンプル分布のムラ(局所密度)を考慮して仲間外れ(外れ値)を見つけるアルゴリズムです。
scikit-learn の LocalOutlierFactor を用いて、LOFのコードを書き、テキストの理論・数式・図による説明を補助しようと思います!
■ インポート
### インポート
import numpy as np
import scipy.stats as stats
from sklearn.neighbors import LocalOutlierFactor
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')■ データの作成
3つのグループのデータを作成します。
2つのグループは正規分布乱数です。
正規分布パラメータを変えるなどして、いろんなデータでLOFできるかもです。
### データの作成
# 乱数シードの固定
seed = 123
# 第1グループのデータ作成
x1 = np.linspace(0, 0.8, 10)
y1 = stats.norm.rvs(loc=-0.5, scale=0.3, size=len(x1), random_state=seed)
# 第2グループのデータ作成
x2 = np.linspace(1.2, 2, 10)
y2 = stats.norm.rvs(loc=0.5, scale=0.3, size=len(x2), random_state=seed)
# 第3グループ:外れ値のデータ作成
x3 = np.array([1.7])
y3 = np.array([-1])
# データを1変数にまとめる
xy = np.stack([np.hstack([x1, x2, x3]), np.hstack([y1, y2, y3])]).T
groups = np.hstack([np.ones(len(x1)), np.ones(len(x2))*2,
np.ones(len(x3))*3]).astype(int)
# 散布図の描画
plt.figure(figsize=(7, 3))
sns.scatterplot(x=xy[:, 0], y=xy[:, 1], hue=groups, s=100, palette='tab20')
plt.title('LOF用データの散布図')
plt.legend(title='グループ', bbox_to_anchor=(1, 1))
plt.grid(lw=0.5);【実行結果】
グループ3が外れ値です!

■ LOF の実行
scikit-learn の LocalOutlierFactor の出番です!
初めて使うのでドキドキします💓
$${k=2}$$個の近傍サンプルを考慮する設定「n_neighbors=2」をしました。
LOFで得たラベルを用いて、外れ値を特定する散布図を描画します。
### LOFの実行
## LOF
# LOF分類器の設定
clf_lof = LocalOutlierFactor(n_neighbors=2)
# LOFの実行
lof_labels = clf_lof.fit_predict(xy)
# ラベルの変更 外れ値:1, 通常値:0
lof_labels = np.where(lof_labels == -1, 1, 0)
## LOFで得たラベルの描画
# 描画領域の指定
plt.figure(figsize=(7, 3))
# LOFで得たラベルを加味してxyの散布図を描画
sns.scatterplot(x=xy[:, 0], y=xy[:, 1], hue=lof_labels, palette='tab10', s=100)
# 修飾
plt.title('LOFラベルで外れ値を識別した散布図')
plt.legend(loc='upper left', title='外れ値:1')
plt.grid(lw=0.5);【実行結果】
LOFで外れ値を特定できました!

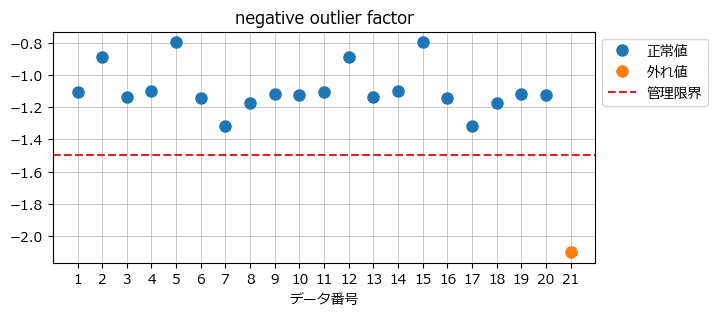
■ LOF 値の描画
符号(プラス・マイナス)が逆転した LOF 値は LOF分類器(clf_lof)の「negative_outlier_factor_」で取り出せます。
また、外れ値のラベリングの閾値(6.5節の管理限界)は LOF分類器(clf_lof)の「offset_」で取り出せます。
描画してみましょう!
### トレーニングサンプルの反対側のLOF(negative outlier factor)の描画
# 描画領域の指定
fig, ax = plt.subplots(figsize=(7, 3))
# 外れ値以外のnegative outlier factorの描画
ax.plot(range(1, xy.shape[0]), clf_lof.negative_outlier_factor_[:-1], 'o',
ms=8, color='tab:blue', label='正常値')
# 外れ値のnegative outlier factorの描画
ax.plot([xy.shape[0]], clf_lof.negative_outlier_factor_[-1], 'o',
ms=8, color='tab:orange', label='外れ値')
# 管理限界の描画
ax.axhline(clf_lof.offset_, color='tab:red', ls='--', label='管理限界')
# 修飾
ax.set(xticks=range(1, xy.shape[0]+1), xlabel='データ番号',
title='negative outlier factor')
ax.legend(bbox_to_anchor=(1, 1))
ax.grid(lw=0.5);【実行結果】
キレイな判別ですね!
なお、正負を反転させる見せ方もあるそうです。
意外とあっさりLOFを試すことができました。

6.2 アイソレーションフォレスト
アイソレーションフォレスト(iForest)は、ランダムフォレストを異常検知に活用しています。
「異常なサンプルはランダムフォレストの個々の決定木のルートに近い部分で分類される」という特徴を利用しています。
scikit-learn の IsolationForest を用いて、iForestのコードを書き、テキストの理論・数式・図による説明を補助しようと思います!
■ iforestの実行
LOFと同じデータを利用して、iForestを実行します。
初めて使うのでドキドキします💓
IsolationForest の引数を試行錯誤して結果を得ました。
### IsolationForest
## 追加インポート
from sklearn.ensemble import IsolationForest
## IsolationForestの実行
# IsolationForest分類器の設定
clf_if = IsolationForest(n_estimators=1000, # 弱学習器の数
contamination=0.05, # データセットの汚染の量
bootstrap=True, # ブートストラップサンプリング
random_state=123) # 乱数シード
# IsolationForestの実行 ラベル値 -1:外れ値, 1:通常値
if_labels = clf_if.fit_predict(xy)
# ラベルの変更 外れ値:1, 通常値:0
if_labels = np.where(if_labels == -1, 1, 0)
## IsolationForestで得たラベルの描画
# 描画領域の指定
plt.figure(figsize=(7, 3))
# LOFで得たラベルを加味してxyの散布図を描画
sns.scatterplot(x=xy[:, 0], y=xy[:, 1], hue=if_labels, palette='tab10', s=100)
# 修飾
plt.title('Isolation Forest用データの散布図')
plt.legend(loc='upper left', title='外れ値:1')
plt.grid(lw=0.5);【実行結果】
iForestで外れ値を特定できました!
なお、IsolationForest の引数 n_estimators や contamination を少しいじるだけで、ぜんぜん違う結果が得られます。
ぜひ試行錯誤を試してみてください。

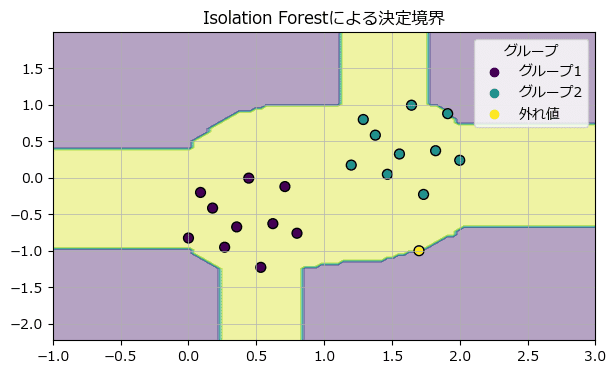
■ おまけ
scikit-learn の公式サイトで分類の決定境界描画コードを発見しました!
試してみましょう。
### 決定境界の描画
# https://scikit-learn.org/stable/auto_examples/ensemble/plot_isolation_forest.html
# 追加インポート
from sklearn.inspection import DecisionBoundaryDisplay
# 描画領域の指定
fig, ax = plt.subplots(figsize=(7, 4))
# IsolationForest分類器の結果から決定境界を描画
disp = DecisionBoundaryDisplay.from_estimator(
clf_if, xy, response_method='predict', alpha=0.4, ax=ax)
# データの散布図の描画
scatter = ax.scatter(xy[:, 0], xy[:, 1], c=groups, s=50, ec='black')
# 修飾
handles, labels = scatter.legend_elements()
ax.legend(handles=handles, labels=['グループ1', 'グループ2', '外れ値'],
title='グループ')
ax.set_title('Isolation Forestによる決定境界')
ax.grid(lw=0.5);【実行結果】

6.3 多変量統計的プロセス管理(MSPC)
多変量統計的プロセス管理(MSPC)は変数間の相関関係の変化に着目して、$${T^2}$$統計量と$${Q}$$統計量を用いて異常検知します。
背後には主成分分析(PCA)が蠢いています。
詳しくはテキストをお読みください!
scikit-learn に MSPC を見つけることができなかったので、テキストオリジナルコードのMSPC関数 を活用させていただきます。
■ データの作成
テキストの図6.6を意識してサンプルデータを作成します。
### データの作成
## 設定
# 乱数生成器の設定
rng = np.random.default_rng(seed=1234)
# 2変量正規分布のパラメータの設定
mean = [0, 0] # mean
rho = 0.75 # 相関係数 ★この値の変更することで正常値の相関関係が変わる
sigma = [0.5, 0.5] # 標準偏差
# 多変量正規分布の共分散行列の作成
cov = [[sigma[0]**2, sigma[0] * sigma[1] * rho],
[sigma[0] * sigma[1] * rho, sigma[1]**2]]
## データの作成
# 正常値:2変量正規分布乱数
data_normaly = rng.multivariate_normal(mean=mean, cov=cov, size=100)
# 異常値
data_anomaly = np.array([[-0.9, 0.9], [0.9, -0.9]])
# データを1つの変数にまとめる
data = np.vstack([data_normaly, data_anomaly])
# 正常値0、異常値1のラベルの作成
data_labels = np.hstack([np.zeros(len(data_normaly)), np.ones(len(data_anomaly))]
).astype(int)データの形状、冒頭数件、異常値を表示します。
## データの冒頭部分の表示
print('data.shape: ', data.shape)
print('\ndata_normalyの最初の3件')
print(data[:3, :])
print('\ndata_anomaly')
print(data[-2:, :])【実行結果】

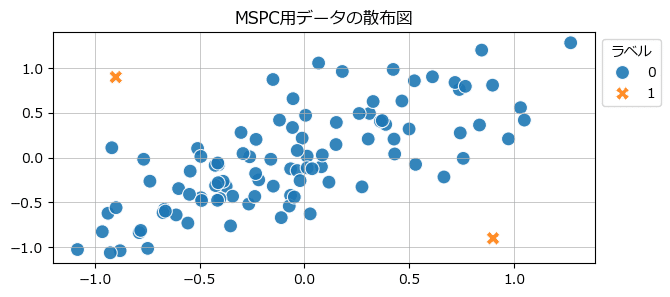
散布図を描画してみましょう。
## データの散布図の描画
plt.figure(figsize=(7, 3))
sns.scatterplot(x=data[:, 0], y=data[:, 1], hue=data_labels, style=data_labels,
s=100, alpha=0.9)
plt.title('MSPC用データの散布図')
plt.legend(title='ラベル', bbox_to_anchor=(1, 1))
plt.grid(lw=0.5);【実行結果】
オレンジの×印が異常値です。
■ MSPC の実行
テキストオリジナルのMSPC関連コードを利用して、MSPCを実行します。
$${T^2}$$統計量と$${Q}$$統計量を描画しましょう。
### MSPCの実行例
## 追加インポート テキストのmspc.pyを利用
from mspc import mspc_ref, mspc_T2Q
## MSPCの学習
meanX, stdX, U, S, V = mspc_ref(data_normaly, 2)
## 予測: T2統計量・Q統計量の算出
# 正常値データで予測
T2_normaly, Q_normaly = mspc_T2Q(data_normaly, meanX, stdX, U, S, V)
# 異常値データで予測
T2_anomaly, Q_anomaly = mspc_T2Q(data_anomaly, meanX, stdX, U, S, V)
## T2統計量の描画
# 描画領域の指定
fig, ax = plt.subplots(figsize=(7, 3))
# 正常値のT2統計量の散布図の描画
ax.scatter(range(1, len(T2_normaly)+1), T2_normaly, color='tab:blue',
ec='white', alpha=0.8, s=70, label='正常値')
# 異常値のT2統計量の散布図の描画
ax.scatter(range(len(T2_normaly)+1, len(T2_normaly)+len(T2_anomaly)+1),
T2_anomaly, color='tab:orange', alpha=0.8, s=70, label='異常値')
# 修飾
ax.set(title='$T^2$ 統計量', xlabel='データ番号', ylabel='$T^2$ 統計量')
ax.legend(bbox_to_anchor=(1, 1))
ax.grid(lw=0.5);
## Q統計量の描画
# 描画領域の指定
fig, ax = plt.subplots(figsize=(7, 3))
# 正常値のQ統計量の散布図の描画
ax.scatter(range(1, len(Q_normaly)+1), Q_normaly, color='tab:blue',
ec='white', alpha=0.8, s=70, label='正常値')
# 異常値のQ統計量の散布図の描画
ax.scatter(range(len(Q_normaly)+1, len(Q_normaly)+len(Q_anomaly)+1),
Q_anomaly, color='tab:orange', alpha=0.8, s=70, label='異常値')
# 修飾
ax.set(title='$Q$ 統計量', xlabel='データ番号', ylabel='$Q$ 統計量')
ax.legend(bbox_to_anchor=(1, 1))
ax.grid(lw=0.5);【実行結果】
$${T^2}$$統計量では、正常値と異常値がくっきり分離されている感じがします。
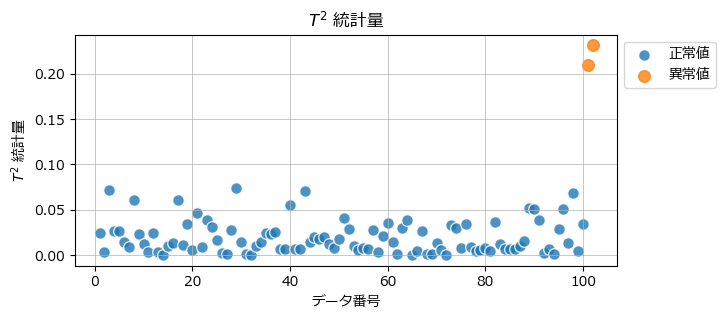
$${Q}$$統計量では、正常値と異常値がやや近くて、区別が難しそうな感じがします。


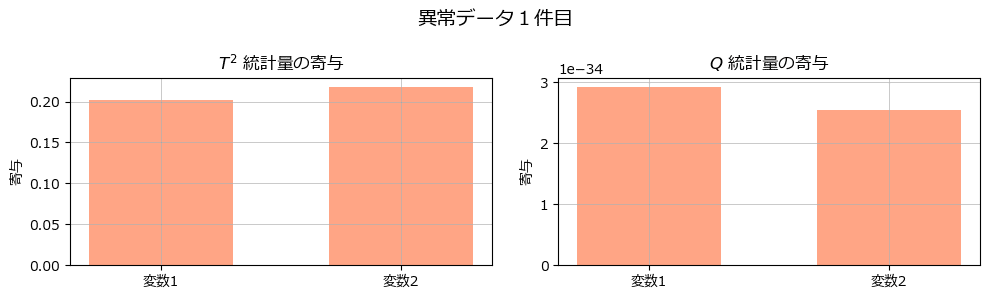
■ 異常値の寄与プロット
6.3.3項「寄与プロットによる異常診断」を実践してみます。
テキストオリジナルのMSPC関連コードを利用します。
### 異常値の寄与プロット
## 追加インポート テキストのmspc.pyを利用
from mspc import cont_T2Q
## T2統計量とQ統計量の寄与を算出
cont_T2, cont_Q = cont_T2Q(data_anomaly, meanX, stdX, U, S, V)
## 異常データの1件目の描画
# 描画領域の指定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 3))
#T2統計量の寄与プロット
ax1.bar(range(1, len(cont_T2)+1), cont_T2[0, :], width=0.6, color='coral',
alpha=0.7)
ax1.set_xticks(ticks=range(1, len(cont_T2)+1), labels=['変数1', '変数2']);
ax1.set(title='$T^2$ 統計量の寄与', ylabel='寄与')
ax1.grid(lw=0.5)
# Q統計量の寄与プロット
ax2.bar(range(1, len(cont_Q)+1), cont_Q[0, :], width=0.6, color='coral',
alpha=0.7)
ax2.set_xticks(ticks=range(1, len(cont_Q)+1), labels=['変数1', '変数2']);
ax2.set(title='$Q$ 統計量の寄与', ylabel='寄与')
ax2.grid(lw=0.5)
# 全体修飾
fig.suptitle('異常データ1件目', fontsize=14)
plt.tight_layout()
plt.show()
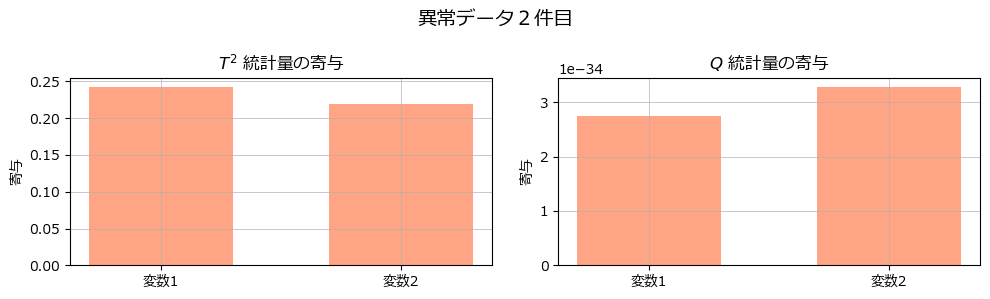
## 異常データの2件目の描画
# 描画領域の指定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 3))
#T2統計量の寄与プロット
ax1.bar(range(1, len(cont_T2)+1), cont_T2[1, :], width=0.6,color='coral',
alpha=0.7)
ax1.set_xticks(ticks=range(1, len(cont_T2)+1), labels=['変数1', '変数2']);
ax1.set(title='$T^2$ 統計量の寄与', ylabel='寄与')
ax1.grid(lw=0.5)
# Q統計量の寄与プロット
ax2.bar(range(1, len(cont_Q)+1), cont_Q[1, :], width=0.6, color='coral',
alpha=0.7)
ax2.set_xticks(ticks=range(1, len(cont_Q)+1), labels=['変数1', '変数2']);
ax2.set(title='$Q$ 統計量の寄与', ylabel='寄与')
ax2.grid(lw=0.5)
# 全体修飾
fig.suptitle('異常データ2件目', fontsize=14)
plt.tight_layout();【実行結果】
んー、2変数の異常検知の寄与はどんぐりの背比べでしょうか・・・
■ 管理限界を示した散布図の描画
6.5節「管理限界の調整」の管理限界を示した$${T^2}$$統計量・$${Q}$$統計量のプロットを再描画してみましょう。
テキストオリジナルのMSPC関連コードを利用します。
信頼区間$${alpha=0.99}$$にしました。
### 管理限界を示したプロット alpha=0.99
## 追加インポート テキストのmspc.pyを利用
from mspc import mspc_CL
## MSPCによるT2統計量とQ統計量の管理限界の算出
CL_T2, CL_Q = mspc_CL(T2_normaly, Q_normaly, alpha=0.99)
## T2統計量の描画
# 描画領域の指定
fig, ax = plt.subplots(figsize=(7, 3))
# 正常値のT2統計量の散布図の描画
ax.scatter(range(1, len(T2_normaly)+1), T2_normaly, color='tab:blue',
ec='white', alpha=0.8, s=70, label='正常値')
# 異常値のT2統計量の散布図の描画
ax.scatter(range(len(T2_normaly)+1, len(T2_normaly)+len(T2_anomaly)+1),
T2_anomaly, color='tab:orange', alpha=0.8, s=70, label='異常値')
# T2統計量の管理限界の描画
ax.axhline(CL_T2, color='tab:red', ls='--', label='管理限界')
# 修飾
ax.set(title='$T^2$ 統計量', xlabel='データ番号', ylabel='$T^2$ 統計量')
ax.legend(bbox_to_anchor=(1, 1))
ax.grid(lw=0.5);
## Q統計量の描画
# 描画領域の指定
fig, ax = plt.subplots(figsize=(7, 3))
# 正常値のQ統計量の散布図の描画
ax.scatter(range(1, len(Q_normaly)+1), Q_normaly, color='tab:blue',
ec='white', alpha=0.8, s=70, label='正常値')
# 異常値のQ統計量の散布図の描画
ax.scatter(range(len(Q_normaly)+1, len(Q_normaly)+len(Q_anomaly)+1),
Q_anomaly, color='tab:orange', alpha=0.8, s=70, label='異常値')
# Q統計量の管理限界の描画
ax.axhline(CL_Q, color='tab:red', ls='--', label='管理限界')
# 修飾
ax.set(title='$Q$ 統計量', xlabel='データ番号', ylabel='$Q$ 統計量')
ax.legend(bbox_to_anchor=(1, 1))
ax.grid(lw=0.5);【実行結果】
$${T^2}$$統計量・$${Q}$$統計量ともに、管理限界を境界にして正常値と異常値の線引きができました。



6.6 時系列データの取り扱い
時系列データにおいても、自己相関を用いることでMSPCによる異常検知ができるそうです。
という事で、サンプルデータを探してきて、時系列MSPCを試してみましょう。
■ データの作成
テキスト図6.13に用いている「きゅうりの価格」を模してみます。
テキストは「都内の2016年~2021年」のデータを政府統計サイト eStat で取得したそうです。
この記事では、「小売物価統計調査による価格推移|日本の物価」様(URL: https://jpmarket-conditions.com/)の「全国のきゅうり1kg価格推移 / 2024年1月までの過去109ヵ月」データ(https://jpmarket-conditions.com/1434/)を利用させていただきます。
「小売物価統計調査による価格推移|日本の物価」様、ありがとうございます!
【引用元サイト】
上記サイトの行見出し「調査月 物価調査都市 価格」から「最古月の行」(今回は2015年1月)までを範囲指定してコピーし、テキストファイルに貼付けしてファイル名「kyuri.txt」で保存します。
TAB区切り形式になるはずです。
その後、次のコードを実行します。
### きゅうりの価格データの作成
## 追加インポート
import pandas as pd
from datetime import datetime
## データの読み込み
data_ts = pd.read_csv('./data/kyuri.txt', sep='\t', usecols=[0, 2])
## データの加工
# 年月から年月日に変更
data_ts['調査月'] = (data_ts['調査月']
.apply(lambda x:datetime.strptime(x+'1日', '%Y年%m月%d日')))
# 日付を昇順ソート
data_ts.sort_values(by='調査月', axis=0, inplace=True)
# 日付をインデックス化
data_ts.set_index('調査月', inplace=True)
# 価格の円を削除
data_ts['価格'] = data_ts['価格'].str.strip('円').astype(int)
# データの保存
data_ts.to_csv('./data/kyuri.csv', encoding='utf_8_sig')
## データの表示
display(data_ts)【実行結果】
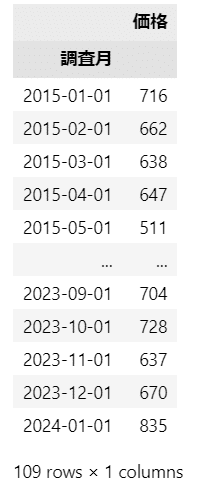
改めて、作成したデータを読み込みします。
### データの読み込み
data_ts = pd.read_csv('./data/kyuri.csv', parse_dates=[0], index_col=0)
display(data_ts)【実行結果】


■ 可視化~折れ線グラフ
ひとまず時系列折れ線グラフを描画して、価格の傾向を見てみましょう。
### データの時系列折れ線グラフの描画
fig, ax = plt.subplots(figsize=(10, 4))
ax.plot(data_ts, lw=0.9)
ax.set(xlabel='年月', ylabel='価格/kg', title='全国のキュウリの価格/kg推移')
plt.grid(lw=0.5);【実行結果】
テキストに記載の通り「冬・夏の価格上下」の周期性がありそうです。

■ 可視化~季節分解
周期性を確認する目的で、季節分解をしてみます。
statsmodels の seasonal_decompose を利用します。
12周期を設定します。
### トレンド成分、季節成分、不規則成分に分離して可視化
## 追加インポート
from statsmodels.tsa.seasonal import seasonal_decompose
## 変動要素の分解の実行 周期性=12
result = seasonal_decompose(data_ts, model='additive', period=12)
## 描画
# 描画領域の設定
fig, ax = plt.subplots(nrows=4, ncols=1, figsize=(8, 8), sharex=True)
# 原系列
ax[0].set_title('原系列')
ax[0].plot(result.observed, lw=0.8)
ax[0].grid(lw=0.5)
# トレンド変動
ax[1].set_title('トレンド変動')
ax[1].plot(result.trend, lw=0.8)
ax[1].grid(lw=0.5)
# 季節変動
ax[2].set_title('季節変動:周期性')
ax[2].plot(result.seasonal, lw=0.8)
ax[2].grid(lw=0.5)
# 不規則変動
ax[3].set_title('不規則変動')
ax[3].plot(result.resid, 'o', alpha=0.5)
ax[3].axhline(0, color='black', ls='--')
ax[3].grid(lw=0.5)
plt.tight_layout();【実行結果】
季節変動はキレイな12か月周期を描いています!
トレンドは山あり 谷ありの様相を醸しています。

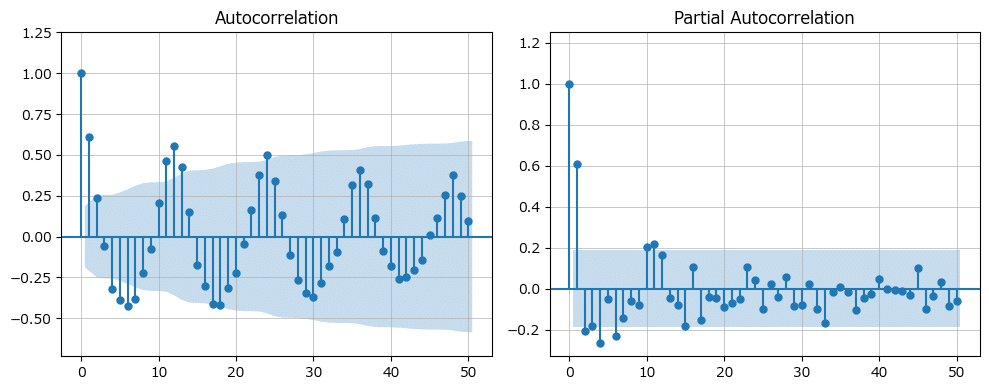
■ 可視化~自己相関・偏自己相関
きゅうり価格の自己相関を確認しましょう。
statsmodels の 自己相関プロット、偏自己相関プロットを利用します。
### 自己相関、偏自己相関の可視化
## 追加インポート
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# 描画領域の設定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 4))
# 自己相関の描画
plot_acf(data_ts, lags=50, auto_ylims=True, ax=ax1)
ax1.grid(lw=0.5)
# 偏自己相関の描画
plot_pacf(data_ts, lags=50, auto_ylims=True, ax=ax2)
ax2.grid(lw=0.5)
plt.tight_layout();【実行結果】
左の自己相関プロット(Autocorrelation)より、12か月周期が分かります。
右の偏自己相関プロット(Partial Autocorrelation)より、ラグ1(1か月ずれ)の相関がはっきり見られます。

■ MSPCの実行
まずMSPC用にデータを加工します。
ラグ1~12の変数を追加します。
### 時系列データのMSPC
## 初期値設定
# ラグ数
k = 12
## MSPC用のデータ作成
data_ts_mspc = data_ts.copy()
for i in range(1, k+1):
col_name = f'lag_{i}'
data_ts_mspc[col_name] = data_ts_mspc['価格'].shift(i)
data_ts_mspc.dropna(axis=0, inplace=True)
display(data_ts_mspc)【実行結果】

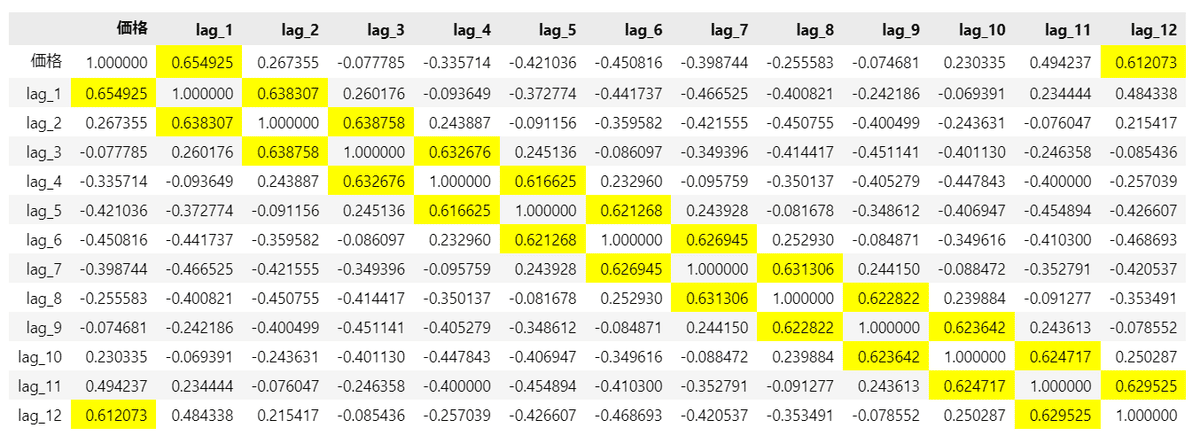
このデータの相関行列を確認します。
## 相関行列の算出
display(data_ts_mspc.corr().style.map(lambda x: 'background-color: yellow'
if (abs(x) > 0.6) & (abs(x) < 1) else ''))【実行結果】
相関係数$${0.6 < r < 1}$$に色を付けてみました。
1か月違い(ラグ1)と12か月違い(ラグ12、12周期)のセルの相関係数が大きいようです。
ではではMSPCの実行です。
主成分数は5、信頼区間は 0.99 です。
以後のコードはテキストオリジナルのMSPC関連コードを利用しています。
## MSPCの実行
# MSPCの学習 numPC=5
meanX, stdX, U, S, V = mspc_ref(data_ts_mspc.values, numPC=5)
# 予測: T2統計量・Q統計量の算出
T2_ts, Q_ts = mspc_T2Q(data_ts_mspc.values, meanX, stdX, U, S, V)
# MSPCによるT2統計量とQ統計量の管理限界の算出 alpha=0.99
CL_T2_ts, CL_Q_ts = mspc_CL(T2_ts, Q_ts, alpha=0.99)$${T^2}$$統計量と$${Q}$$統計量を描画しましょう。
## T2統計量の描画
# 描画領域の指定
fig, ax = plt.subplots(figsize=(7, 3))
# 正常値のT2統計量の散布図の描画
ax.scatter(data_ts_mspc.index, T2_ts, color='tab:blue',
ec='white', alpha=0.8, s=70, label='正常値')
# T2統計量の管理限界の描画
ax.axhline(CL_T2_ts, color='tab:red', ls='--', label='管理限界')
# 修飾
ax.set(title='$T^2$ 統計量', xlabel='年月', ylabel='$T^2$ 統計量')
ax.legend(bbox_to_anchor=(1, 1))
ax.grid(lw=0.5);
## Q統計量の描画
# 描画領域の指定
fig, ax = plt.subplots(figsize=(7, 3))
# 正常値のQ統計量の散布図の描画
ax.scatter(data_ts_mspc.index, Q_ts, color='tab:blue',
ec='white', alpha=0.8, s=70, label='正常値')
# Q統計量の管理限界の描画
ax.axhline(CL_Q_ts, color='tab:red', ls='--', label='管理限界')
# 修飾
ax.set(title='$Q$ 統計量', xlabel='年月', ylabel='$Q$ 統計量')
ax.legend(bbox_to_anchor=(1, 1))
ax.grid(lw=0.5);【実行結果】
異常値が紛れ込んでいないようです。


管理限界を超えるデータの年月を調べてみましょう。
$${T^2}$$統計量です。
### T2統計量が管理限界以上の年月
data_ts_mspc[T2_ts >= CL_T2_ts]['価格'].to_frame()【実行結果】

$${Q}$$統計量です。
### Q統計量が管理限界以上の年月
data_ts_mspc[Q_ts >= CL_Q_ts]['価格'].to_frame()【実行結果】

2つの統計量で異常検知の結果が異なるんですね。

Tennessee Eastman プロセスの異常検知
第6章の総仕上げであり、第6章で初めて異常検知アルゴリズムを動かすのがこのTennessee Eastman プロセスの異常検知なのです。
LOF、iForest、MSPC、オートエンコーダで異常検知します。
データは Harvard DataVerse から取得します。
この記事では、異常データ「IDV1」を用いて、①テキストの誤植等の補正、②異常検知結果のプロットコードの関数化を取り扱います。
なお、記事のコードを動かすにはテキストオリジナルコードを使用する必要があります。
ぜひ、テキストとテキストオリジナルコードをお読みください!
① 誤植等の補正
■ プログラム6.8 MSPCでの異常検知
関数 mspc_T2Q に与える train データに .values をつける方が動きが安定する印象です。
【補正前(抜粋)】
# 管理限界の取得
T2_train, Q_train = mspc_T2Q(train_data, meanX, stdX, U, S, V) # MSPC
CL_T2_mspc, CL_Q_mspc = mspc_CL(T2_train, Q_train, alpha=0.99) # 管理限界
# 異常データのT2統計量とQ統計量の計算
T2_mspc, Q_mspc = mspc_T2Q(faulty_data, meanX, stdX, U, S, V) # MSPC【補正後(抜粋)】
# 管理限界の取得 ★ Xには.valuesを付けるほうがいい
T2_train, Q_train = mspc_T2Q(train_data.values, meanX, stdX, U, S, V) # MSPC
CL_T2_mspc, CL_Q_mspc = mspc_CL(T2_train, Q_train, alpha=0.99) # 管理限界
# 異常データのT2統計量とQ統計量の計算 ★ Xには.valuesを付けるほうがいい
T2_mspc, Q_mspc = mspc_T2Q(faulty_data.values, meanX, stdX, U, S, V) # MSPC■ プログラム6.12 AEでのT²統計量とREの計算
autoencoder.py の AE_T2RE 関数の一部に誤植があります。
「RE_AE[i] = Q[0]」のところを「RE_AE[i] = RE[0]」に変更します。
【補正前(抜粋)】
for i in range(len(z)):
z_vec = np.reshape(z[i], (len(z[i]), 1))
T2 = (z_vec - z_hat).T @ np.linalg.inv(S_z) @ (z_vec - z_hat)
RE = (X[i] - xhat[i])**2
T2_AE[i] = T2[0]
RE_AE[i] = Q[0] # ★変更前
return T2_AE, RE_AE【補正後(抜粋)】
for i in range(len(z)):
z_vec = np.reshape(z[i], (len(z[i]), 1))
T2 = (z_vec - z_hat).T @ np.linalg.inv(S_z) @ (z_vec - z_hat)
RE = (X[i] - xhat[i])**2
T2_AE[i] = T2[0]
RE_AE[i] = RE[0] # ★変更後
return T2_AE, RE_AE■ プログラム6.13 AEでの管理限界の決定
train_data の再読み込みをすると、次行の AE_T2RE 実行時に「tensorに変換されていない」というエラーが発生します。
また、2行目の z_hat は作成されていないのでエラーが発生します。
【補正前(抜粋)】
# 管理限界の決定
train_data = pd.read_csv('./data/normal_data.csv') # 正常データの読み込み
T2_train, RE_train = AE_T2RE(model, train_data, z_hat, S_z)
CL_T2_AE, CL_RE_AE = mspc_CL(T2_train, RE_train, alpha=0.99)【補正後(抜粋)】
# 管理限界の決定
T2_train, RE_train = AE_T2RE(model, train_data, z_bar, S_z) # ★z_bar
CL_T2_AE, CL_RE_AE = mspc_CL(T2_train, RE_train, alpha=0.99)■ プログラム6.14 AEでの異常検知
プログラム6.13 と同様に z_hat の変更が必要です。
【補正後(抜粋)】
# T2統計量、REの計算
T2_AE, RE_AE = AE_T2RE(model, faulty_data, z_bar, S_z) # ★z_bar
② 異常検知結果プロットの関数化
LOF、iForest、MSPC、オートエンコーダ(AE)の異常検知結果をほぼ一括して処理するようにコードを改造します。
テキストの処理の流れに沿って、テキストオリジナルコードを適宜実行しつつ、この記事のコードを実行します。
■ プログラム6.15 異常検知結果のプロット
LOFとiforest用のプロット関数です。
テキストオリジナルコードを拝借しています。
# LOFとiForestのスコア描画関数の定義
def plot_lof_if(algo_name, data_name, score, CL):
# 描画領域の指定
plt.figure(figsize=(10, 3))
# スコアの描画 LOFとIsolation Forestでは絶対値を計算する
plt.plot(list(range(1, 961)), abs(score), color='tab:blue', lw=0.7)
# 管理限界の水平線の描画
plt.axhline(abs(CL), color='tab:red', ls='--', label='管理限界')
# 異常発生時刻の垂直線の描画
plt.axvline(160, color='gray', lw=2, label='異常発生時点')
# 修飾
plt.xlim(1, 960)
# plt.ylim(0, 10)
plt.xlabel('Sample')
plt.ylabel('Score')
plt.title(algo_name + ' : ' + data_name)
plt.grid(lw=0.5)
plt.legend()
plt.show()LOFの異常検知結果をプロットします。
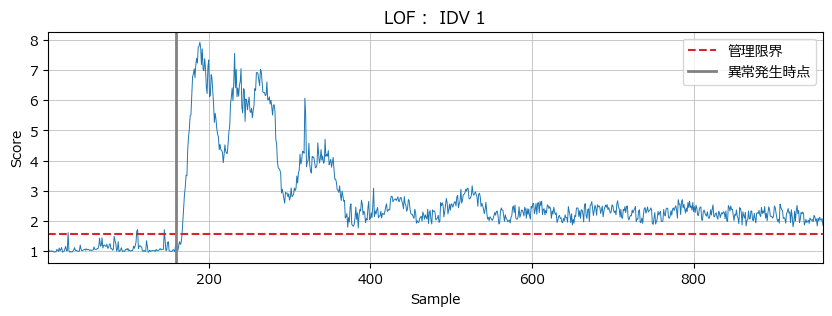
# LOFの異常検知結果の描画
plot_lof_if('LOF', 'IDV 1', score_lof, CL_lof)【実行結果】
異常発生時刻 160 を境に、LOFの異常度は管理限界を超えています。
うまく異常を表現できているようです。
iForestの異常検知結果をプロットします。
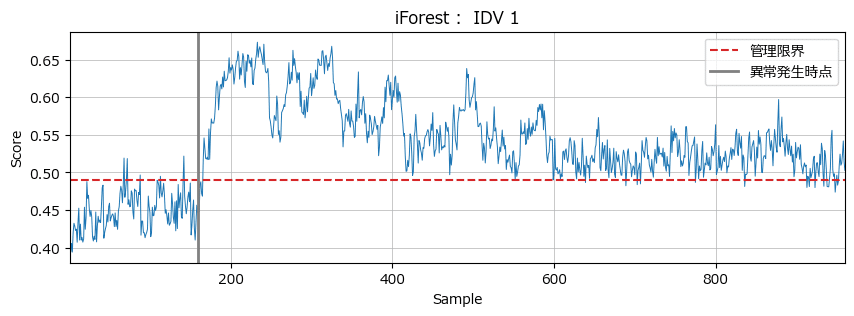
# Isolation forestの異常検知結果の描画
plot_lof_if('iForest', 'IDV 1', score_if, CL_if)【実行結果】
iForestも異常をキャッチできているようです。
LOFと比べると異常発生時は緩やかにキャッチしている感じです。
MSPCとAE用のプロット関数です。
2つの統計量を描画します。
テキストオリジナルコードを拝借しています。
# MSPCとAEのスコア描画関数の定義 ※テキストのコードを引用、一部改変
def plot_MSPC_AE(algo_name, data_name, T2, CL_T2, Q, CL_Q):
## 初期値 2つ目のグラフのylabel
if algo_name == 'MSPC':
y_label = '$Q$ 統計量'
else:
y_label = '$RE$'
## 描画領域の指定
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 7))
## T2統計量
# T2統計量の描画
ax1.plot(list(range(1, 961)), T2, color='tab:blue', lw=0.7)
# T2統計量の管理限界の水平線の描画
ax1.axhline(CL_T2, color='tab:red', ls='--', label='管理限界')
# 異常発生時刻の垂直線の描画
ax1.axvline(160, color='gray', lw=2, label='異常発生時点')
# 修飾
ax1.set(xlim=(1, 960), xlabel='Sample', ylabel='$T^2$ 統計量',
title=algo_name + ' : ' + data_name)
ax1.grid(lw=0.5)
ax1.legend()
## Q統計量/RE
# Q統計量/REの描画
ax2.plot(list(range(1, 961)), Q, color='tab:blue', lw=0.7)
# Q統計量/REの管理限界の水平線の描画
ax2.axhline(CL_Q, color='tab:red', ls='--', label='管理限界')
# 異常発生時刻の垂直線の描画
ax2.axvline(160, color='gray', lw=2, label='異常発生時点')
# 修飾
ax2.set(xlim=(1, 960), xlabel='Sample', ylabel=y_label)
ax2.grid(lw=0.5)
ax2.legend()
plt.tight_layout()
plt.show()MSPCの異常検知結果をプロットします。
# MSPCの異常検知結果の描画
plot_MSPC_AE('MSPC', 'IDV 1', T2_mspc, CL_T2_mspc, Q_mspc, CL_Q_mspc)【実行結果】
MSPCも時点160から異常をうまくキャッチされているようです。
また160より前の時点の正常データが管理限界付近に張り付いている感じがします。

オートエンコーダ(AE)の異常検知結果をプロットします。
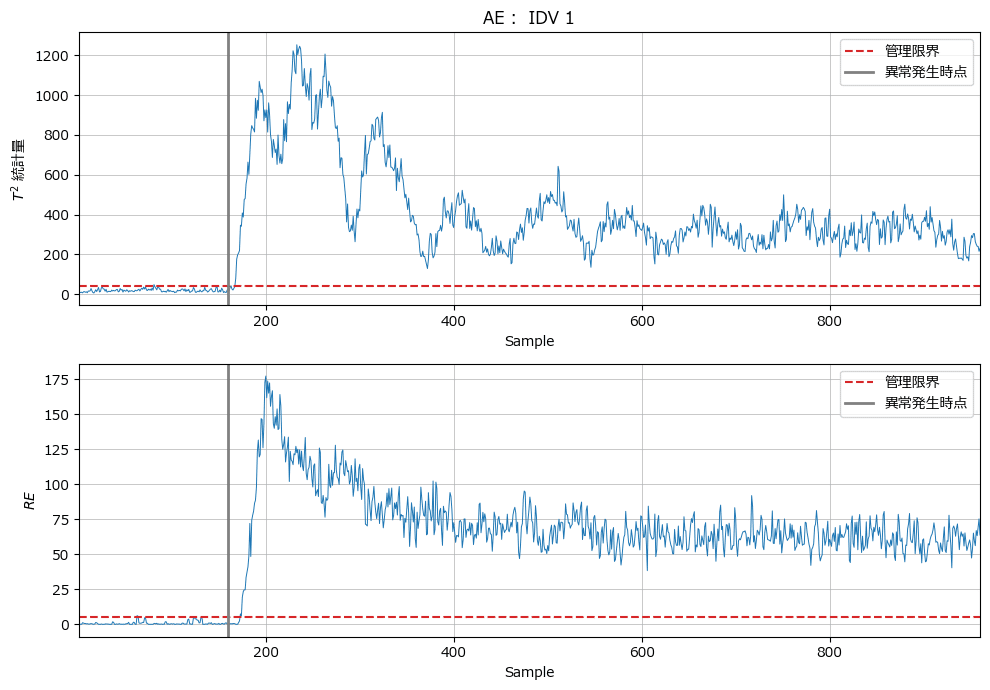
# AEの異常検知結果の描画
plot_MSPC_AE('AE', 'IDV 1', T2_AE, CL_T2_AE, RE_AE, CL_RE_AE)【実行結果】
AEも時点160の少し後から異常をキャッチしているいるようです。
また160より前の時点の正常データがMSPCと同様に管理限界付近に張り付いている感じがします。
テキストの記載通り、管理限界を上方に変更することで、正常データを異常に誤検知する可能性が少なくなるかもしれません。

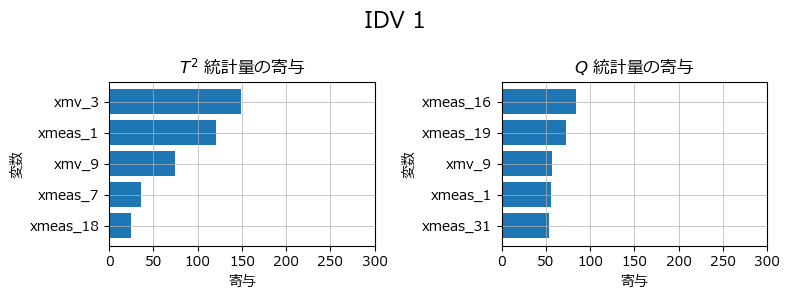
■ プログラム6.16 寄与プロット
MSPCの異常度に寄与する説明変数のトップ5を表示するように、テキストのコードを改造します。
## 追加インポート
from mspc import cont_T2Q
## 描画用データの作成
# 寄与の計算 faulty_dataはcsv読み込み時点のデータフレームです
cont_T2, cont_Q = cont_T2Q(faulty_data.values, meanX, stdX, U, S, V)
# 異常発生後100サンプルの寄与の平均を計算
fault_cont_T2 = np.average(cont_T2[160:260, :], axis=0)
fault_cont_Q = np.average(cont_Q[160:260, :], axis=0)
# T2の上位5変数の特定: 降順TOP5のindexを取得→値と変数名を取得
T2_top5_idx = np.argsort(fault_cont_T2, axis=0)[::-1][:5][::-1]
fault_cont_T2_top5 = fault_cont_T2[T2_top5_idx]
T2_top5_labels = faulty_data.columns[T2_top5_idx]
# Qの上位5変数の特定: 降順TOP5のindexを取得→値と変数名を取得
Q_top5_idx = np.argsort(fault_cont_Q, axis=0)[::-1][:5][::-1]
fault_cont_Q_top5 = fault_cont_Q[Q_top5_idx]
Q_top5_labels = faulty_data.columns[Q_top5_idx]
## 描画処理
# ticksの設定
ticks = range(1, 6)
# 描画領域の指定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 3))
# T2のプロット
ax1.barh(ticks, fault_cont_T2_top5)
ax1.set(title='$T^2$ 統計量の寄与', xlabel='寄与', ylabel='変数',
xlim=(0, 300))
ax1.set_yticks(ticks=ticks, labels=T2_top5_labels)
ax1.grid(lw=0.5)
# Qのプロット
ax2.barh(ticks, fault_cont_Q_top5)
ax2.set(title='$Q$ 統計量の寄与', xlabel='寄与', ylabel='変数',
xlim=(0, 300))
ax2.set_yticks(ticks=ticks, labels=Q_top5_labels)
ax2.grid(lw=0.5)
# 全体修飾
fig.suptitle('IDV 1', fontsize=16)
plt.tight_layout()
plt.show()【実行結果】
テキスト図6.23上に相当するグラフです。
テキストと同じ結果になりました!やったね!
第6章の寄り道写経は以上です。

テキストの最終章・第7章は寄り道写経をしませんでした。
したがいまして今回の記事がシリーズ最終回となります。
書籍「スモールデータ解析と機械学習」の実践はとても楽しかったです。
ブログをお読みの皆様がこの書籍を楽しむ姿を想像して筆を置きます。
ご清聴ありがとうございました。

シリーズの記事
次の記事

前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
