第９章「練習テストのフィードバックの効果」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング２」の第９章「練習テストのフィードバックの効果」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
この章では、学校のテスト（試験）において、答案用紙を返す際に先生がどんなフィードバック（戻し方）をすると学生の学習効果が上がるのか、をベイズ推論します。
テスト結果のフィードバック効果については、多くの研究が報告されているそうで、テキストは先行研究結果に基づく分析「メタ分析」を行っています。
ではでは、PyMCのベイズモデリングの世界を楽しんでまいりましょう！
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 ： 山森光陽 先生
モデル難易度： ★★★★★ （難しい）
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★★★★ & GoooD! \\
結果再現度 & ★★★★★ & 最高✨ \\
楽しさ & ★★★★★ & 楽しい！ \\
\end{array}
$$
評価ポイント
２回連続でテキストの結果とほぼ一致！
嬉しいです！！！この章で最も困難なコードの１つは「フォレストプロット」でした。
サマリー済みのデータをもとに描画するので、arviz の plot_forest を使うことができず、matplotlib でゴリゴリ描きました。
可視化は奥が深いです。
工夫・喜び・反省
もう１つの困難なコードはテキスト末尾の表9.4「従来型のメタ分析」でした。
一時は棄権を考えましたが、ふらりとWeb検索を続けていたら、statsmodels の meta_analysys にたどり着きました！
見つけました！粘り勝ちです！！
ただし、テキストの結果に寄せるように引数を調整しているだけなので、果たして正しく使えているのか、不安はあります。
モデルの概要
テキストの調査・実験の概要
「テストの結果をどのように返したら学習効果が上がるのか」については、世界中で「テスト実施→フィードバック→事後テスト実施・結果測定」を分析する研究がなされているようです。
本章の分析は、すでに実施済みの他者研究データ（先行研究データ）をさらに分析する「メタ分析」です。
調査・実験の概要をギュッと圧縮して図にしました！
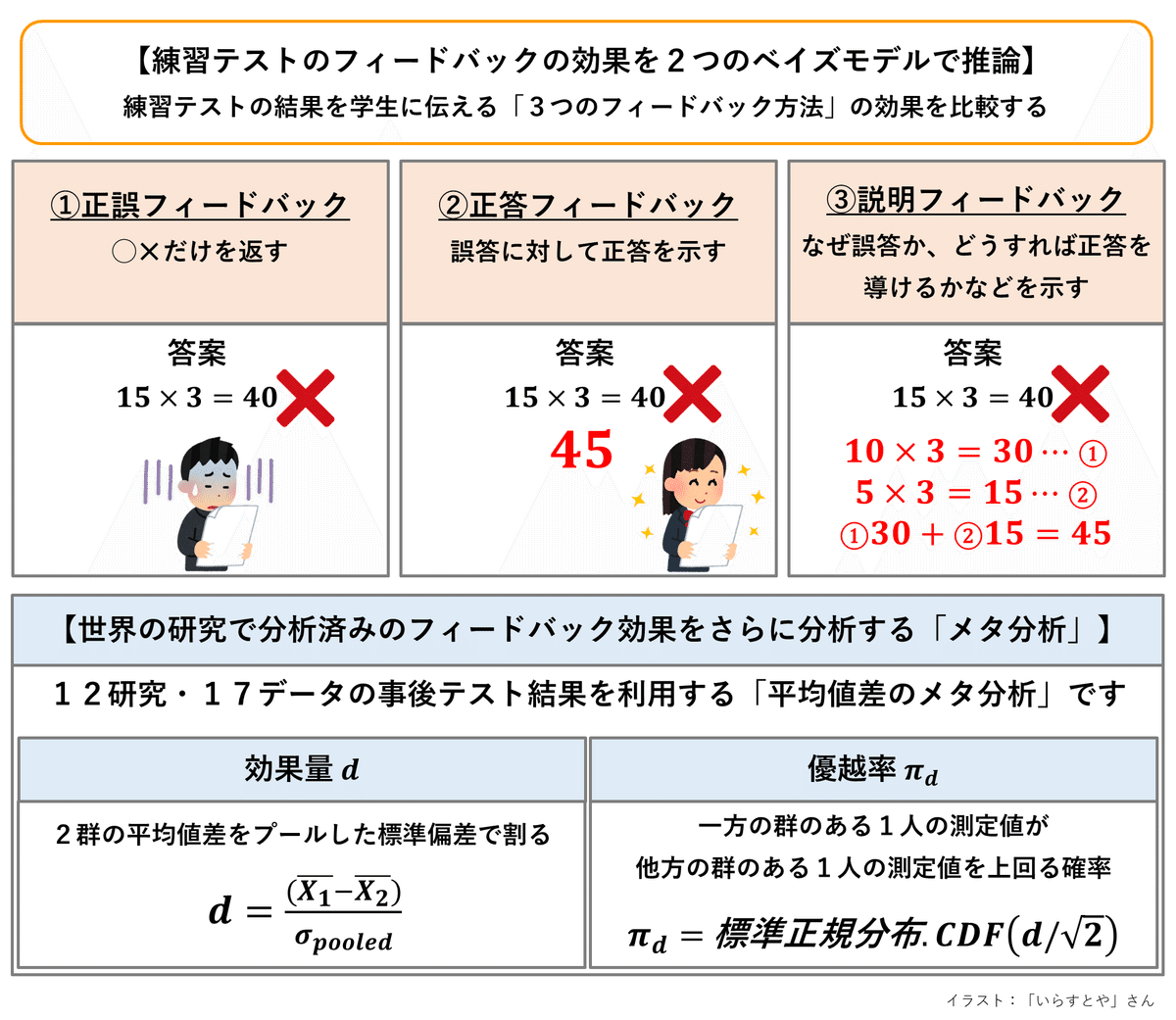
■ テスト結果の3つのフィードバックの種類
次の３つのフィードバックの効果を比較します。
正誤フィードバック（$${rw}$$）：正解・不正解のみを返す
正答フィードバック（$${ca}$$）：正答を返す
説明フィードバック（$${ex}$$）：正答を説明する
■ 先行研究
１２の研究に含まれる１７のデータを利用します。
１７のデータはフィードバック種類のうちの１つの効果を測定しています。
例えば、正誤フィードバックの研究データの場合は、「正誤フィードバックをするグループ（実験群）」と「フィードバックしないグループ（統制群）」という２群を比べています。
■ 効果量$${d}$$と優越率$${\pi_d}$$
２つの指標についてテキストの説明をお借りします。
効果量$${d}$$は２群の平均値差を次のプールした標準偏差で割った値です。
（$${SD^2}$$はおそらく標本の不偏分散だと思われます）
$$
\sigma_{pooled} = \sqrt{\cfrac{(n_1-1)SD^2_1+(n_2-1)SD^2_2}{n_1+n_2-2}}
$$
効果量$${d}$$は分布のズレを意味するそうです。
あるフィードバックの有無（介入の有無）による効果量が$${d=0.5}$$の場合、２群の得点の分布が$${0.5}$$標準偏差分ズレているという意味です。
なお、テキストで用いる先行研究データには執筆者の先生が再計算した効果量$${d}$$が設定されています。
優越率$${\pi_d}$$は一方の群のある１人の測定値が他方の群のある１人の測定値を上回る確率のことだそうです。
上記図に効果量$${d}$$との関係式を掲げました。
効果量$${d}$$を$${\sqrt{2}}$$で割った値について、標準正規分布の累積分布関数で確率を求める感じです。
テキストのモデリング
【モデル１】フィードバック種類を考慮しない効果を推論するモデル
■ 目的変数と関心のあるパラメータ
目的変数は効果量の$${d_i}$$です。
添字$${i}$$は各研究です（$${i=1, \cdots ,17}$$）。
関心のあるパラメータは平均効果量$${\mu}$$と優越率$${\pi_d}$$です。
最初のモデルは「フィードバック全般の効果」に焦点を合わせています。
■ モデル数式
$${es_i}$$は研究$${i}$$ごとに異なる効果です。
また$${se_i}$$は研究$${i}$$ごとの効果量の標準偏差であり、データに設定されています。
記号$${\Phi(\cdot)}$$は標準正規分布の累積分布関数です。
$$
\begin{align*}
d_i &\sim \text{Normal}\ (es_i,\ se_i) \\
\pi_{\mu} &= \Phi \left( \cfrac{\mu}{\sqrt{2}} \right) \\
es_i &\sim \text{Normal}\ (\mu,\ \sigma_i) \\
\sigma_i &\sim \text{HalfStudentT}\ (4,\ 0,\ 5) \\
\mu &\sim \text{Uniform}\ (-10,\ 10) \\
\end{align*}
$$
【モデル２】フィードバック種類による効果の違いを推論するモデル
フィードバック種類ごとにモデルを作成します。
正誤フィードバック$${rw}$$を例にして数式を掲載します。
正答フィードバックは$${ca}$$、説明フィードバックは$${ex}$$で読み替えしてください。
■ 目的変数と関心のあるパラメータ
目的変数は効果量の$${d_{rw_i}}$$です。
関心のあるパラメータは平均効果量$${\mu_{rw}}$$と優越率$${\pi_{\mu_{rw}}}$$です。
■ モデル数式
$$
\begin{align*}
d_{rw_i} &\sim \text{Normal}\ (es_{rw_i},\ se_{rw_i}) \\
\pi_{\mu_{rw}} &= \Phi \left( \cfrac{\mu_{rw}}{\sqrt{2}} \right) \\
es_{rw_i} &\sim \text{Normal}\ (\mu_{rw},\ \sigma_{rw_i}) \\
\sigma_{rw_i} &\sim \text{HalfStudentT}\ (4,\ 0,\ 5) \\
\mu_{rw} &\sim \text{Uniform}\ (-10,\ 10) \\
\end{align*}
$$
■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCの自己流モデルの推論値を利用した分析は「PyMC実装」章をご覧ください。
PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
１．インポート
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
import scipy.stats as stats
# PyMC
import pymc as pm
import arviz as az
# メタ分析
from statsmodels.stats import meta_analysis
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')２．データの読み込み
csvファイル「fdata.csv」をpandasのデータフレームに読み込みます。
### データの読み込み
data = pd.read_csv('fbdata.csv')
display(data)【実行結果】
１７研究データです。列の意味は次のとおりです（？は自信が無いです）。
・Author：論文の著者
・Year：論文発行年
・Study：研究論文中の研究番号
・Feedback：フィードバック種類（利用しない変数）
・fb：フィードバック種類の略称
・n：標本サイズ
・d：効果量
・var：効果量の分散（？）
・se：効果量の標準誤差
３．データの前処理
データに優越率を付加します。
その前にテキスト95ページの優越率$${\pi_d}$$の例示を計算してみましょう。
標準正規分布の累積分布関数には scipy.stats の norm.cdf を利用しました。
### テキスト95ページの効果量dと優越率πdの計算
# FB方法と効果量のデータフレームの作成
example_df = pd.DataFrame({'FB方法': ['正誤', '正答', '説明'],
'効果量_d': [0.03, 0.64, 0.44]})
# 優越率の算出
example_df['優越率_πd'] = stats.norm.cdf(example_df['効果量_d'] / np.sqrt(2))
# データフレームの表示
display(example_df.round(3))【実行結果】
だいたいテキストと一致していると思います。
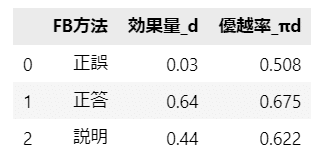
数字の読み方例をテキストからお借りします。
正答フィードバックは、効果量が$${0.64}$$なので$${0.64}$$標準偏差分の平均点を上げる効果が見られ、優越率は$${60\%}$$を超える最も効果の高いフィードバックである、と解釈できます。
では前処理に進みます。
### 優越率πdの追加 πd=norm.cdf(d/√2)
data['πd'] = stats.norm.cdf(data['d'] / np.sqrt(2))
display(data)【実行結果】
データに優越率 πd を追加しました。
４．データの外観の確認
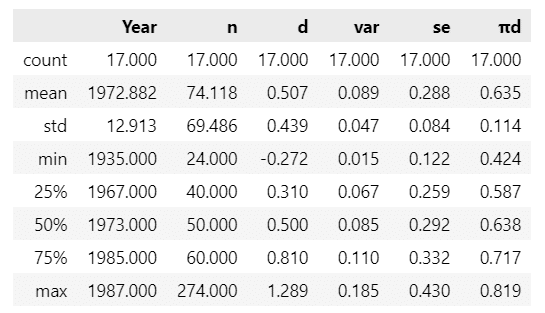
要約統計量を表示します。
### 要約統計量の表示
data.describe().round(3)【実行結果】
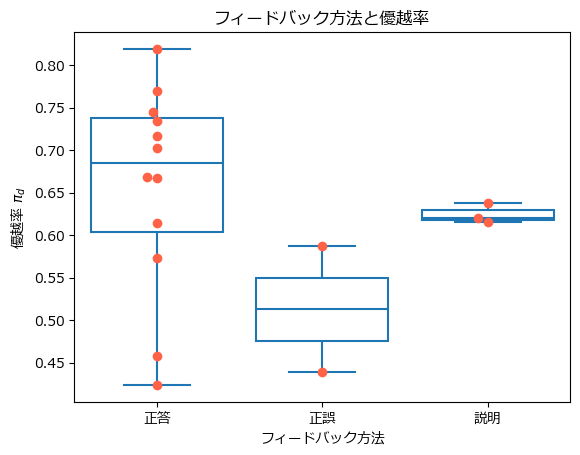
フィードバック種類別に優越率を可視化しましょう。
箱ひげ図を描画します。
### フィードバック方法と優越率の描画
ax = sns.boxplot(data=data, x='Feedback', y='πd', fill=False)
ax = sns.swarmplot(data=data, x='Feedback', y='πd', color='tomato', size=7)
ax.set(xlabel='フィードバック方法', ylabel='優越率 $\pi_d$',
xticklabels=['正答', '正誤', '説明'], title='フィードバック方法と優越率');【実行結果】
赤い点は観測値（各研究の優越率）です。
いっけん、正答フィードバックの優越率が高く、正答フィードバックが最も効果が高いように見えます。
ただ正誤フィードバックと説明フィードバックはデータ数が少ないですね。
モデル１：フィードバック種類を考慮しない効果を推論するモデル
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
$${\text{dims}=study}$$は、当該変数の形状（shape）が研究$${i}$$の個数$${17}$$であることを示しています。
$$
\begin{align*}
\mu &\sim \text{Uniform}\ (\text{lower}=-10,\ \text{upper}=10) \\
\sigma &\sim \text{HalfStudentT}\ (\text{nu}=4,\ \text{sigma}=5,\ \text{dims}=study) \\
es &\sim \text{Normal}\ (\text{mu}=\mu,\ \text{sigma}=\sigma,\ \text{dims}=study) \\
likelihood &\sim \text{Normal}\ (\text{mu}=es,\ \text{sigma}=se,\ \text{dims}=study)
\end{align*}
$$
１．モデルの定義
数式表現を実直にモデル記述します。
### モデルの定義
with pm.Model() as model1:
### データ関連定義
## coordの定義
model1.add_coord('study', values=data.index, mutable=True)
## dataの定義
# 効果量 d
d = pm.ConstantData('d', value=data['d'].values, dims='study')
# 標準誤差 SE
se = pm.ConstantData('se', value=data['se'].values, dims='study')
### 事前分布
## 各研究iごとに異なる変量効果
# 平均効果量 μ
mu = pm.Uniform('mu', lower=-10, upper=10)
# 標準偏差
sigma = pm.HalfStudentT('sigma', nu=4, sigma=5, dims='study')
# 効果 es
es = pm.Normal('es', mu=mu, sigma=sigma, dims='study')
### 尤度
# 効果量dは平均効果量μと標準誤差変数seをパラメータにもつ正規分布に従う
likelihood = pm.Normal('likelihood', mu=es, sigma=se, observed=d,
dims='study')【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の１つを設定しました。データの行の座標：名前「study」、値「行インデックス」
dataの定義
次の２つを設定しました。効果量：d （目的変数）
標準誤差：se
パラメータの事前分布
モデルの数式表現のとおりです。
尤度
正規分布です。
２．モデルの外観の確認
# モデルの表示
model1【実行結果】
シンプルなモデルです。
### モデルの可視化
pm.model_to_graphviz(model1)【実行結果】
シンプルな階層ベイズモデルです。
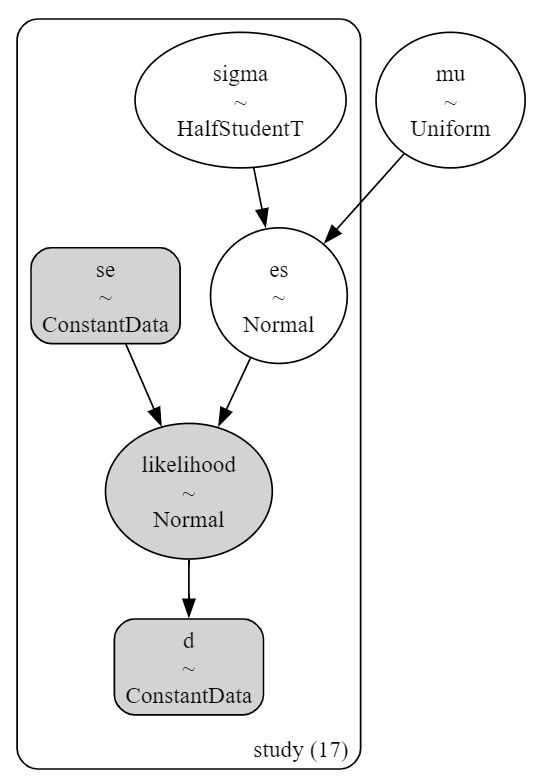
３．事後分布からのサンプリング
乱数生成数はテキストよりも少ないです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ30秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 30秒
# テキスト: iter=100000, warmup=50000, chains=4
with model1:
idata1 = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.99,
nuts_sampler='numpyro', random_seed=1234)【実行結果】
４．サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$とします。
ここでは$${\hat{R} > 1.01}$$のパラメータが無いことを確認します。
### r_hat>1.1の確認
# 設定
idata_in = idata1 # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
$${\hat{R} > 1.01}$$のパラメータは０件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。
ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
pm.summary(idata1, hdi_prob=0.95, round_to=3)【実行結果】
中程に mu の事後分布統計量が表示されています。
平均 0.529、95%HDI [ 0.154, 0.939 ] です。
トレースプロットで事後分布サンプリングデータの様子を確認します。
### トレースプロットの表示
pm.plot_trace(idata1, compact=True, divergences=False)
plt.tight_layout();【実行結果】
左のグラフから、４本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。
ただし、実は発散を示すバーコードが多数見受けられます。
plot_trace() の引数 divergences=False を指定してバーコードを非表示にしています。
５．分析
テキストにならって分析します。
１７の研究の平均効果量$${\mu}$$と優越率$${\pi_{\mu}}$$を表示します。
テキストの表9.2に相当します
### 17の研究を対象としたメタ分析のパラメータの事後分布の要約統計量 ※表9.2に相当
## 定義・設定
# 事後統計量算出関数の定義
def calc_stats(x):
ci = np.quantile(x, q=[0.025, 0.5, 0.975])
return np.mean(x), np.std(x), ci[0], ci[1], ci[2]
# 優越率算出関数の定義
def calc_pi(x):
return stats.norm.cdf(x=x/np.sqrt(2), loc=0, scale=1)
# 初期値設定
columns = ['EAP', 'post.sd', '2.5%CI', 'MED', '97.5%CI']
## 要約統計量の算出
# 推論データからmuの取り出し
mu_sample = idata1.posterior.mu.data.flatten()
# muの事後統計量の算出
mu_stats = calc_stats(mu_sample)
# muの効果量pi_muを算出して、pi_muの事後統計量を算出
pi_mu_stats = calc_stats(calc_pi(mu_sample))
# データフレーム化
stats_df1 = pd.DataFrame({'μ': mu_stats, 'πμ': pi_mu_stats}, index=columns).T
# データフレームの表示
display(stats_df1.round(2))【実行結果】
テキストとほぼ一致しています。
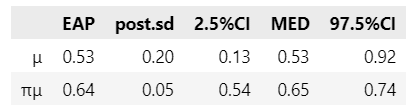
【分析】
$${\mu}$$の95%信用区間が０を含んでいないことから、練習テストの実施後にフィードバック（どの種類かは問わない）を行う方が事後テストの得点が高いことが示されている、と見ることができるようです。
$${\pi_{\mu}}$$の95%信用区間が$${[0.54, 0.74]}$$であることから、何らかのフィードバックを与えられた学生がフィードバックを受けていない学生の得点を上回る確率は、95%の確信をもって、少なくとも$${\boldsymbol{54\%}}$$より大きく、多くとも$${\boldsymbol{74\%}}$$程度である、と解釈できるようです。
６．推論データの保存
推論データを再利用する（かもしれない）場合に備えてファイルに保存しましょう。
idata1をpickleで保存します。
### idataの保存 pickle
file = r'idata1_ch09.pkl'
with open(file, 'wb') as f:
pickle.dump(idata1, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata1_ch09.pkl'
with open(file, 'rb') as f:
idata1_load = pickle.load(f)
モデル２：フィードバック種類による効果の違いを推論するモデル
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
フィードバック種類ごとに分けて書きます。
$$
\begin{align*}
\mu_{rw} &\sim \text{Uniform}\ (\text{lower}=-10,\ \text{upper}=10) \\
\sigma_{rw} &\sim \text{HalfStudentT}\ (\text{nu}=4,\ \text{sigma}=5,\ \text{dims}=study_{rw}) \\
es_{rw} &\sim \text{Normal}\ (\text{mu}=\mu_{rw},\ \text{sigma}=\sigma_{rw},\ \text{dims}=study_{rw}) \\
likelihood_{rw} &\sim \text{Normal}\ (\text{mu}=es_{rw},\ \text{sigma}=se_{rw},\ \text{dims}=study_{rw}) \\
\\
\mu_{ca} &\sim \text{Uniform}\ (\text{lower}=-10,\ \text{upper}=10) \\
\sigma_{ca} &\sim \text{HalfStudentT}\ (\text{nu}=4,\ \text{sigma}=5,\ \text{dims}=study_{ca}) \\
es_{ca} &\sim \text{Normal}\ (\text{mu}=\mu_{ca},\ \text{sigma}=\sigma_{ca},\ \text{dims}=study_{ca}) \\
likelihood_{ca} &\sim \text{Normal}\ (\text{mu}=es_{ca},\ \text{sigma}=se_{ca},\ \text{dims}=study_{ca}) \\
\\
\mu_{ex} &\sim \text{Uniform}\ (\text{lower}=-10,\ \text{upper}=10) \\
\sigma_{ex} &\sim \text{HalfStudentT}\ (\text{nu}=4,\ \text{sigma}=5,\ \text{dims}=study_{ex}) \\
es_{ex} &\sim \text{Normal}\ (\text{mu}=\mu_{ex},\ \text{sigma}=\sigma_{ex},\ \text{dims}=study_{ex}) \\
likelihood_{ex} &\sim \text{Normal}\ (\text{mu}=es_{ex},\ \text{sigma}=se_{ex},\ \text{dims}=study_{ex}) \\
\end{align*}
$$
フィードバック種類
・$${rw}$$：正誤フィードバック
・$${ca}$$：正答フィードバック
・$${ex}$$：説明フィードバック
１．モデルの定義
データをフィードバック種類ごとに分割します。
### フィードバック方法別にデータ分割
data_rw = data[data['fb']=='rw'].reset_index(drop=True) # 正誤
data_ca = data[data['fb']=='ca'].reset_index(drop=True) # 正答
data_ex = data[data['fb']=='ex'].reset_index(drop=True) # 説明数式表現を実直にモデル記述します。
### モデルの定義
with pm.Model() as model2:
### データ関連定義
## coordの定義
model2.add_coord('studyRw', values=data_rw.index, mutable=True)
model2.add_coord('studyCa', values=data_ca.index, mutable=True)
model2.add_coord('studyEx', values=data_ex.index, mutable=True)
## dataの定義
# 効果量 d
dRw = pm.ConstantData('dRw', value=data_rw['d'].values, dims='studyRw')
dCa = pm.ConstantData('dCa', value=data_ca['d'].values, dims='studyCa')
dEx = pm.ConstantData('dEx', value=data_ex['d'].values, dims='studyEx')
# 標準誤差 SE
seRw = pm.ConstantData('seRw', value=data_rw['se'].values, dims='studyRw')
seCa = pm.ConstantData('seCa', value=data_ca['se'].values, dims='studyCa')
seEx = pm.ConstantData('seEx', value=data_ex['se'].values, dims='studyEx')
### 事前分布
# フィードバック方法ごとの平均効果量 μ
muRw = pm.Uniform('muRw', lower=-10, upper=10)
muCa = pm.Uniform('muCa', lower=-10, upper=10)
muEx = pm.Uniform('muEx', lower=-10, upper=10)
# 標準偏差
sigmaRw = pm.HalfStudentT('sigmaRw', nu=4, sigma=5, dims='studyRw')
sigmaCa = pm.HalfStudentT('sigmaCa', nu=4, sigma=5, dims='studyCa')
sigmaEx = pm.HalfStudentT('sigmaEx', nu=4, sigma=5, dims='studyEx')
# 効果 es
esRw = pm.Normal('esRw', mu=muRw, sigma=sigmaRw, dims='studyRw')
esCa = pm.Normal('esCa', mu=muCa, sigma=sigmaCa, dims='studyCa')
esEx = pm.Normal('esEx', mu=muEx, sigma=sigmaEx, dims='studyEx')
### 尤度
# 効果量dは平均効果量μと標準誤差変数seをパラメータにもつ正規分布に従う
likeliRw = pm.Normal('likeliRw', mu=esRw, sigma=seRw, observed=dRw,
dims='studyRw')
likeliCa = pm.Normal('likeliCa', mu=esCa, sigma=seCa, observed=dCa,
dims='studyCa')
likeliEx = pm.Normal('likeliEx', mu=esEx, sigma=seEx, observed=dEx,
dims='studyEx')【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は３つのデータのインデックスを設定しました。正誤フィードバックデータの行の座標：名前「studyRw」、値「行インデックス」
正答フィードバックデータの行の座標：名前「studyCa」、値「行インデックス」
説明フィードバックデータの行の座標：名前「studyEx」、値「行インデックス」
dataの定義
次の３つのデータごとに２つを設定しました。
以下は正誤フィードバックの例です。効果量：dRw （目的変数）
標準誤差：seRw
パラメータの事前分布
モデルの数式表現のとおりです。
尤度
フィードバック種類ごとに３つの尤度関数を設定しています
いずれも正規分布に従います。
２．モデルの外観の確認
# モデルの表示
model2【実行結果】
モデル１の３倍の数式です。
### モデルの可視化
pm.model_to_graphviz(model2)【実行結果】
３つのモデルが独立して並んでいます（剪定後の三本松みたい！？）
３．事後分布からのサンプリング
乱数生成数はテキストよりも少ないです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ30秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 30秒
# テキスト: iter=100000, warmup=50000, chains=4
with model2:
idata2 = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.95,
nuts_sampler='numpyro', random_seed=1234)【実行結果】
４．サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$とします。
ここでは$${\hat{R} > 1.01}$$のパラメータが無いことを確認します。
### r_hat>1.1の確認
# 設定
idata_in = idata2 # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
$${\hat{R} > 1.01}$$のパラメータは０件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。
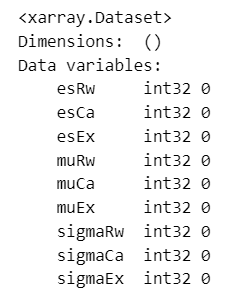
ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
pm.summary(idata1, hdi_prob=0.95, round_to=3)【実行結果】
トレースプロットで事後分布サンプリングデータの様子を確認します。
### トレースプロットの表示
pm.plot_trace(idata2, compact=True, divergences=False)
plt.tight_layout();【実行結果】
左のグラフから、４本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。
ただし、実は発散を示すバーコードが多数見受けられます。
plot_trace() の引数 divergences=False を指定してバーコードを非表示にしています。
５．分析
テキストにならって分析します。
フィードバックの種類ごとの要約統計量等です。
テキストの表9.2に相当します
### フィードバックの種類ごとのパラメータの事後分布の要約統計量 ※表9.3に相当
## 定義・設定
# 事後統計量算出関数の定義
def calc_stats(x):
ci = np.quantile(x, q=[0.025, 0.5, 0.975])
return np.mean(x), np.std(x), ci[0], ci[1], ci[2]
# 優越率算出関数の定義
def calc_pi(x):
return stats.norm.cdf(x=x/np.sqrt(2), loc=0, scale=1)
# 初期値設定
columns = ['EAP', 'post.sd', '2.5%CI', 'MED', '97.5%CI']
## 要約統計量の算出
# 推論データからμの取り出し shape=(3, 4000), 行インデックス 0:rw, 1:cs, 2:ex
mu_rw = idata2.posterior.muRw.stack(sample=('chain', 'draw')).data
mu_ca = idata2.posterior.muCa.stack(sample=('chain', 'draw')).data
mu_ex = idata2.posterior.muEx.stack(sample=('chain', 'draw')).data
# μの事後統計量の算出
mu_rw_stats = calc_stats(mu_rw)
mu_ca_stats = calc_stats(mu_ca)
mu_ex_stats = calc_stats(mu_ex)
# muの効果量πμの算出＆πμの事後統計量の算出
pi_mu_rw_stats = calc_stats(calc_pi(mu_rw))
pi_mu_ca_stats = calc_stats(calc_pi(mu_ca))
pi_mu_ex_stats = calc_stats(calc_pi(mu_ex))
# δの事後統計量の算出
delta_ca_rw_stats = calc_stats(mu_ca - mu_rw)
delta_ex_rw_stats = calc_stats(mu_ex - mu_rw)
delta_ca_ex_stats = calc_stats(mu_ca - mu_ex)
# Uの事後統計量の算出
U_ca_rw_stats = calc_stats(np.where(mu_ca > mu_rw, 1, 0))
U_ex_rw_stats = calc_stats(np.where(mu_ex > mu_rw, 1, 0))
U_ca_ex_stats = calc_stats(np.where(mu_ca > mu_ex, 1, 0))
# データフレーム化
stats_df1 = pd.DataFrame({'μrw': mu_rw_stats,
'μca': mu_ca_stats,
'μex': mu_ex_stats,
'π_μrw': pi_mu_rw_stats,
'π_μca': pi_mu_ca_stats,
'π_μex': pi_mu_ex_stats,
'δ_μca-μrw': delta_ca_rw_stats,
'δ_μex-μrw': delta_ex_rw_stats,
'δ_μca-μex': delta_ca_ex_stats,
'U_δμca-δμrw': U_ca_rw_stats,
'U_δμex-δμrw': U_ex_rw_stats,
'U_δμca-δμex': U_ca_ex_stats,
}, index=columns).T
# データフレームの表示
display(stats_df1.round(2))【実行結果】
テキストとおおむね一致しています。
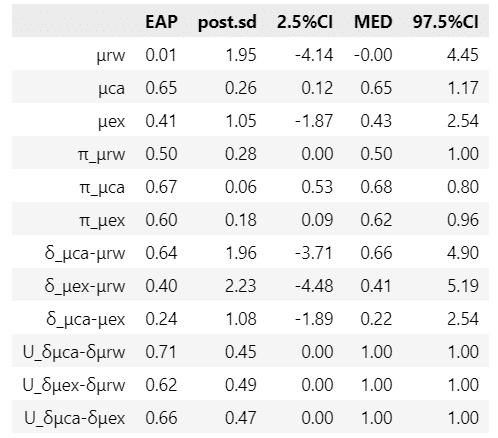
【変数名の説明】
末尾の rw, ca, ex がフィードバックの種類を示しています。
μ はフィードバック種類ごとの平均効果量です。
π はフィードバック種類ごとの優越率です。
δ は２つのフィードバック種類の平均効果量の差です。
例えば、δ_μca-μrw は、正答フィードバック ca の平均効果量から正誤フィードバック rw の平均効果量を引いた値です。
U は $${\mu_{ca}>\mu_{rw},\ \mu_{ex}>\mu_{rw},\ \mu_{ca}>\mu_{ex}}$$という仮説が正しい確率です。
例えば、U_δμca-δμrw は δ_μca-μrw > 0 のときに 1 、これ以外のときに 0 の値を持ちます。
また、平均効果量のフォレストプロットをテキストの図9.1をまねてプロットします。
描画用のデータ「plotdata.csv」が用意されていますので、データを読み込んで描画します。
データの前処理に手こずりました。
### フィードバックの種類別のメタ分析結果のフォレストプロットの描画 ※図9.1に相当
## 研究ごとの要約統計量を記録したデータの読み込み
data2 = pd.read_csv('./plotdata.csv', encoding='cp932')
## データ前処理１：研究ごとの要約統計量データの加工
# 不要レコードの削除
data2.dropna(subset=['研究'], inplace=True)
# FBの種類の欠損値を補完（１つ前の値をセット）
data2['フィードバックの種類'].fillna(method='ffill', inplace=True)
# 列の絞り込み・列名の変更
data2 = data2[['フィードバックの種類', '研究', 'EAP', 'post.sd', 'lo', 'hi']]
data2.columns = ['FB', '研究', 'EAP', 'post.sd', 'lo', 'hi']
## データ前処理２：平均効果量の事後統計量をセット
# FB=正誤rwの事後統計量をセット
data2.loc[(data2['FB']=='正誤') & (data2['研究']=='平均効果量'),\
['EAP', 'post.sd', 'lo', 'hi']]\
= [mu_rw_stats[0], mu_rw_stats[1], mu_rw_stats[2], mu_rw_stats[4]]
# FB=正答caの事後統計量をセット
data2.loc[(data2['FB']=='正答') & (data2['研究']=='平均効果量'),\
['EAP', 'post.sd', 'lo', 'hi']]\
= [mu_ca_stats[0], mu_ca_stats[1], mu_ca_stats[2], mu_ca_stats[4]]
# FB=説明exの事後統計量をセット
data2.loc[(data2['FB']=='説明') & (data2['研究']=='平均効果量'),\
['EAP', 'post.sd', 'lo', 'hi']]\
= [mu_ex_stats[0], mu_ex_stats[1], mu_ex_stats[2], mu_ex_stats[4]]
## データ前処理３：描画データの準備
# data2を降順ソート
data_plt = data2[::-1]
# 研究列の「平均効果量」の名称の変更
data_plt.loc[(data2['FB']=='正誤') & (data_plt['研究']=='平均効果量'), ['研究']]\
= ['平均効果量：正誤 $\\mu_{rw}$']
data_plt.loc[(data2['FB']=='正答') & (data_plt['研究']=='平均効果量'), ['研究']]\
= ['平均効果量：正答 $\\mu_{ca}$']
data_plt.loc[(data2['FB']=='説明') & (data_plt['研究']=='平均効果量'), ['研究']]\
= ['平均効果量：説明 $\\mu_{ex}$']
## 描画処理
# 描画領域の指定
plt.figure(figsize=(7, 7))
# x軸=0の赤い垂直線の描画
plt.axvline(0, color='red', ls='--')
# FB種類ごとにEAP点と95%CIバーを描画
for fb in ['説明', '正答', '正誤']:
# リストのFB種類に該当するデータを抽出
tmp = data_plt[data_plt['FB']==fb]
ax = plt.subplot()
# エラーバーでEAP・95%CIを描画
ax.errorbar(x=tmp.EAP, y=tmp.研究, fmt='o',
xerr=[abs(tmp.lo - tmp.EAP), abs(tmp.hi - tmp.EAP)])
# 修飾
ax.set(xlim=[-5.1, 5.1], xticks=range(-5, 6))
plt.show()【実行結果】
ではテキストの分析過程をお借りして、分析（のマネごと）を行います。
【分析】
■ 平均効果量 μ
平均効果量 μ の95%信用区間が０を含んでいないのは正答フィードバック ca だけです。
したがって、３種類のフィードバックのうち、効果がある（効果が正である）のは正答フィードバックと解釈できます。
■ 優越率 π
正の効果ありと考えられる正答フィードバック ca の優越率 π_μca は平均が$${0.67}$$、95%信用区間が$${[0.53,\ 0.80]}$$です。
正答フィードバックを受けた学生が受けていない学生の得点を上回る確率は、95%の確信をもって、少なくとも$${53\%}$$より大きく、多くとも$${80\%}$$程度である、と解釈できそうです。
■ 平均効果量の差 δ
３つの δ は95%信用区間に０を含んでいるため、フィードバックの種類別の効果に差はみられない、と解釈できるそうです。
そのため、２種類のフィードバックの平均効果量の大小にかかる U も検討に値しない、とのことです。
■ 個人的な感想
正答の説明を与える説明フィードバックがベストかな、と予測していました。
蓋を開けてみると、正しい答えだけを返す正答フィードバックだけが事後テストの得点アップに効果がある、という結果を得ました。
なんだか不思議な感じがします。
正答フィードバックの研究数は１２、説明フィードバックの研究数は３と、分析データ数の大きさが異なっています。
説明フィードバックの研究の数（標本サイズ）が小さいことが、分析結果にも影響している気がいたします（気がするだけ）。
６．変量効果モデルによるメタ分析
最後に、テキストが「ベイズによるメタ分析」と対比する「従来型の変量効果モデルによるメタ分析」を実施します。
テキストの表9.4に相当します。
statsmodels の meta_analysis を利用します。
テキストの表の値に合うようにパラメータ調整しただけですので、statsmodels の使い方の適否は自信がありません。
### 変量効果モデル（従来の方法）によるフィードバック種類別のメタ分析 ※表9.4に相当
# https://www.statsmodels.org/dev/examples/notebooks/generated/metaanalysis1.html
## 初期値設定
# 結果格納データフレームの初期化
stats_df2 = pd.DataFrame()
# フィードバックのラベルと名称
fb_labels = ['rw', 'ca', 'ex']
fb_names = ['正誤', '正答', '説明']
## メタ分析の実施：フィードバック種類ごとに繰り返し計算処理
for (fb, fb_name) in zip(fb_labels, fb_names):
# フィードバック種類のデータ抽出
tmp = data[data['fb']==fb]
# 効果量の取り出し
eff = tmp['d'].values
# 効果量の分散の取り出し
var_eff = tmp['var'].values
# メタ分析を実行して結果をresに格納
res = meta_analysis.combine_effects(eff, var_eff, method_re='iterated')
# メタ分析結果から平均・標準誤差・95%CI区間を取り出してデータフレーム化
res_stats = pd.DataFrame({
f'{fb_name}': res.summary_frame().loc['random effect'][:4]
})
# 結果格納データフレームと結合
stats_df2 = pd.concat([stats_df2, res_stats], axis=1)
## 結果格納データフレームの最終化
stats_df2 = stats_df2.T
stats_df2.columns = ['平均効果量', 'SE', '95%CI下限', '95%CI上限']
stats_df2.index.name = 'フィードバックの種類'
## メタ分析結果の表示
display(stats_df2.round(2))【実行結果】
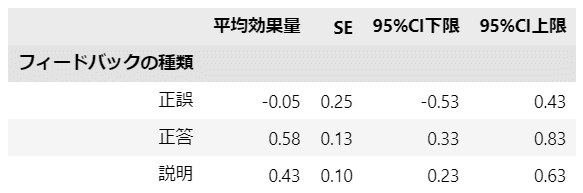
（参考：ベイズによる平均効果量の推論値）
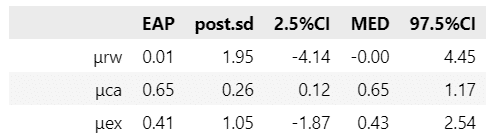
テキストは、従来型のメタ分析と比べて、ベイズのメタ分析の意義を語っています。以下は要約です。
１．信用区間は確率を示す
ベイズの信用区間（テキストは確信区間）は、パラメータ推定値が区間の下限と上限に含まれる確率です。
従来型の「信頼区間」（パラメータ推定値が含まれる確率では無い）よりも直感的に理解しやすいです。
２．パラメータ以外の生成量を計算できる
優越率の事後分布を算出できるなど、生成量を分析に活用できます。
従来型の分析では生成量を用いることができない（感じ）です。
７．推論データの保存
推論データを再利用する（かもしれない）場合に備えてファイルに保存しましょう。
idata2をpickleで保存します。
### idataの保存 pickle
file = r'idata2_ch09.pkl'
with open(file, 'wb') as f:
pickle.dump(idata2, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata2_ch09.pkl'
with open(file, 'rb') as f:
idata2_load = pickle.load(f)
以上で第９章は終了です。
おわりに
テストあれこれ
普段、テストに接することは殆どありません（システム開発のテスト工程を除く）。
直近のことを思い出してみると、資格試験にチャレンジしていましたね。
末尾で受験体験記ブログを紹介させてください。
直近の資格試験はすべて、パソコンで出題・解答する「CBT方式」でした。
CBT方式の多くは試験問題を漏らすことが厳禁されていて、答案のフィードバックなんて貰えない・期待できないのです（泣）
先生の肉筆の採点、懐かしいです。
おわり
【資格試験受験記のご紹介】
統計検定準１級とPythonエンジニア認定データ分析の受験記です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で７つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！
１．のんびり統計
統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
２．実験！たのしいベイズモデリング１＆２をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング２」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは Ｒ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！
３．実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験！岩波データサイエンスvol.1」の４人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう！
４．楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
５．RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん！
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
６．データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
７．Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。