
第5章「樹木の直径と高さとの関係のモデリング」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング2」の第5章「樹木の直径と高さとの関係のモデリング」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
この章では、京都市の天然林の樹木データを用いて、直径と高さの関係をモデリングします。
直径と高さの関係には「拡張相対成長式」が用いられます。
このモデルがあれば、幹の直径の観測値で木の高さを推論できるのです!

しかし今回は、とても複雑なモデル。
無事に収束を迎えることは・・・、できませんでした(泣)
ひとまず、PyMCのベイズモデリングの世界を楽しみましょう。
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 伊東宏樹 先生
モデル難易度: ★★★・・ (ふつう)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★★★・ & ほぼ納得 \\
結果再現度 & ★・・・・ & NG!! \\
楽しさ & ★★★★★ & 楽しい! \\
\end{array}
$$

評価ポイント
テキストおよびStanコードを忠実にPyMCのコードに変換できたと思っていたのですが、収束しませんでした。
$${\hat{R}}$$の値はもう一歩で$${1.1}$$を下回りそうなのですが・・・(残念)。
工夫・喜び・反省
テキストのモデルはなかなかの強敵で、モデルの真意を理解することはできました。
理解は諦めて、テキストのStanコードやMCMC実行コードに忠実なPyMC化を目指しました。
MCMCサンプル実行(pm.sample())時に与えるパラメータの初期値(initvals引数)もテキストのマネをしたのですが、MCMC実行エラーが多発して、対策を見出すまでに時間がかかりました。そのおかげで、引数のデータ型が大切なことを身をもって知ることができました。

モデルの概要
テキストの調査・実験の概要
■ 樹木の直径と高さのモデリングって?
木の高さを測定するのは、かなり手間がかかるそうです。
そこで、一部の木の直径と高さを測ってモデリングし、残りの木は直径だけを測定、モデルを用いて高さを推定するのです。
直径の測定については、一定の高さで幹の周囲を測って円周率で割って直径値とする方法があり、この方法は測定の手間がかからないというわけです。
■ 相対成長
背の高い人は腕も長い、というような関係を相対成長関係と呼ぶそうです。
直径の大きい木は高い、という関係に通じるのでしょうか?
樹木の場合、直径の大きさと木の高さ「樹高」の関係について、次式の「拡張相対式」がよく使われるそうです。
$$
\cfrac{1}{H-H_D} = \cfrac{1}{aD^h} + \cfrac{1}{H_{\text{Max}}} \\
\\
H-H_D = \cfrac{aD^hH_{\text{Max}}}{aD^h+H_{\text{Max}}} \\
$$
$${H}$$は樹高、$${H_D}$$は直径$${D}$$を測定した高さ、$${H_{\text{Max}}}$$は潜在的に取り得る最大の樹高、$${a,h}$$は曲線の形状を決めるパラメータです。
ベイズモデリングでは、下式の両辺の対数を取った数式が用いられます。
【お知らせ】
今回は図示を省略いたします。

■ データの概要
京都市の銀閣寺山間国有林の天然林(二次林)で測定した15種類、232本の木の直径と樹高のデータです。
この国有林は五山送り火で知られる大文字山のふもとにあるそうです。
データは次のサイトで公開されています。
「補足電子資料:表S1~S3(エクセル2007:30KB)」

テキストのモデリング
■目的変数と関心のあるパラメータ
目的変数は、樹高の観測値$${H}$$から直径を測定した高さの観測値$${H_D}$$を差し引いた値「$${H_{ij}-H_D}$$」です。
添字$${i}$$は木のID、$${j}$$は樹高測定回です。
また、樹高と関係のある直径の観測値$${D}$$も目的変数に用います。
関心のあるパラメータに関してはテキストに特に明記されていませんが、おそらく、全パラメータに注目します。
直径から樹高を推定するモデルの構築には、全パラメータが必要だからです。
■ テキストのベイズモデル
テキストの数式、文章補足からモデル数式を書きました。
数式の具体的な内容はぜひ、テキストでお確かめください。
$$
\begin{align*}
H_{ij}-H_D &\sim \text{LogNormal}\ (\log \overline{H}_i,\ \sigma^2_H) \\
D_i &\sim \text{Normal}\ (\overline{D}_i,\ \sigma^2_D) \\
\overline{D}_i &\sim \text{HalfNormal}\ (100^2) \\
\\
\log \overline{H}_i &= \log a_{s_i} + h_{s_i} \log \overline{D}_i + \log H_{\text{Max} s_i} \\
&\quad - \log(a_{s_i}\overline{D}^{h_{s_i}}_i + H_{\text{Max}s_i}) + \varepsilon_i \\
\varepsilon_i &\sim \text{Normal}\ (0,\ \sigma^2) \\
\sigma &\sim \text{HalfNormal}\ (10^2) \\
\\
\log a_s &= \log \overline{a} + \varepsilon_{\text{a}s} \\
\log \overline{a} &\sim \text{Normal}\ (0,\ 10^2) \\
\varepsilon_{\text{a}s} &\sim \text{Normal}\ (0,\ \sigma^2_{\text{a}}) \\
\sigma_{\text{a}} &\sim \text{HalfNormal}\ (10^2) \\
\\
\log h_s &= \log \overline{h} + \varepsilon_{\text{h}s} \\
\log \overline{h} &\sim \text{Normal}\ (0,\ 10^2) \\
\varepsilon_{\text{h}s} &\sim \text{Normal}\ (0,\ \sigma^2_{\text{h}}) \\
\sigma_{\text{h}} &\sim \text{HalfNormal}\ (10^2) \\
\\
\log H_{\text{Max}s} &= \log \overline{H}_{\text{Max}} + \varepsilon_{\text{Hmax s}} \\
\log \overline{H}_{\text{Max}} &\sim \text{Normal}\ (4,\ 4^2) \\
\varepsilon_{\text{Hmax s}} &\sim \text{Normal}\ (0,\ \sigma^2_{\text{Hmax}}) \\
\sigma_{\text{Hmax}} &\sim \text{HalfNormal}\ (10^2) \\
\end{align*}
$$
主要な変数の内容は次のとおりです。
$${H_{ij}}$$:樹高の測定値
$${H_D}$$:樹高を測定した高さ(Stanモデルでは$${1.3m}$$)
$${\overline{H}_i}$$:木の真の高さから$${H_D}$$を差し引いたもの
$${D_i}$$:直径の測定値
$${\overline{D}}$$:真の直径
$${s_i}$$:木の種類
$${a_{s_i}}$$:木の種類ごとに決まる拡張相対成長式のパラメータ$${a}$$
$${h_{s_i}}$$:木の種類ごとに決まる拡張相対成長式のパラメータ$${h}$$
$${H_{\text{Max}s_i}}$$:木の種類ごとに決まる潜在的な最大樹高
$${\overline{a}}$$:パラメータ$${a_{s_i}}$$の全体的な平均
$${\overline{h}}$$:パラメータ$${h_{s_i}}$$の全体的な平均
$${\overline{H}_{\text{Max}}}$$:パラメータ$${H_{\text{Max}s_i}}$$の全体的な平均
$${\varepsilon_{\text{a}}, \varepsilon_{\text{h}}, \varepsilon_{\text{Hmax}}}$$:木の種類$${s}$$によるパラメータ$${a_{s_i},h_{s_i},H_{\text{Max}s_i}}$$の変量効果
■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCの自己流モデルは収束できず、分析に利用できない状況です。

PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.インポート
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# WEBアクセス
import requests
# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')2.データの読み込み
WebサイトからEXCELファイルをダウンロードして分析に用います。
まずダウンロードしましょう。
「path」に「Excelファイルの格納フォルダ+ファイル名」を指定します。
### EXCELファイルのダウンロード
## 初期値設定
# EXCEL(.xlsx)ファイルのURL
url = 'https://www.ffpri.affrc.go.jp/pubs/bulletin/435/documents/tables-s1-s3.xlsx'
# EXCELファイルの格納フォルダ+ファイル名
path = 'tables-s1-s3.xlsx'
## ダウンロード
# Web接続
res = requests.get(url)
# ダウンロードファイルの保存
with open(path, mode='wb') as f:
f.write(res.content)【実行結果】なし
続いて、EXCELファイルをpandasのデータフレームに読み込みます。
### ダウンロードしたEXCELファイルの読み込み
# 初期値設定:列名
cols = ['和名', '学名', 'No', '胸高直径', '樹高1', '樹高2', '樹高3', '樹高4' ]
# EXCELファイルの読み込み
data_orgn = pd.read_excel(path, sheet_name=0, header=None, skiprows=2, names=cols)
# データの表示
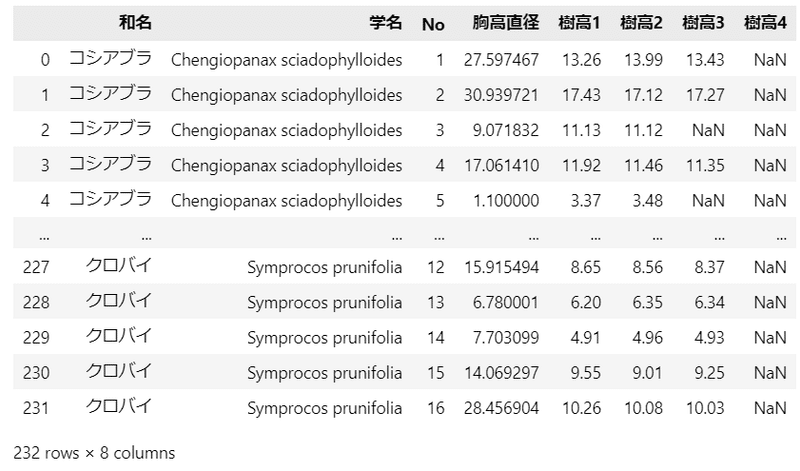
display(data_orgn)【実行結果】
Noは木の個体IDです。
胸高直径の単位はcmです。
樹高は測定回1~測定回4まで横持ちしています。単位はmです。
なお、樹高の測定回数は個体によってまちまちです。
例えば1行目のコシアブラNo.1は3回測定、3行目のコシアブラNo.3は2回測定です。
Excelファイルをダウンロードしない(フォルダに保存しない)で、URLから直接データ参照する場合は、次のコードを実行します。
### 参考:データの読み込み(WEBサイトから直接読み込み)
## 初期値設定
# EXCEL(.xlsx)ファイルのURL
url = 'https://www.ffpri.affrc.go.jp/pubs/bulletin/435/documents/tables-s1-s3.xlsx'
# 列名
cols = ['和名', '学名', 'No', '胸高直径', '樹高1', '樹高2', '樹高3', '樹高4']
## データの読み込み
# データの読み込み
data_orgn = pd.read_excel(url, sheet_name=0, header=None, skiprows=2, names=cols)
# データの表示
display(data_orgn)
# データをcsvファイル形式で保存する場合のコード
# data_orgn.to_csv('data.csv', encoding='utf_8_sig', index=False)
# 参考:保存したcsvファイルの読み込み
# data_orgn = pd.read_csv('data.csv')3.データの外観の確認
樹種(木の種類)ごとにデータの要約統計量を表示します。
テキストの表5.1に相当します。
### データに含まれる木の種類とタイプ・平均直径・平均樹高 ※表5.1に相当
## 初期値設定 樹のタイプ
# 樹のタイプ辞書、各樹のタイプリストの作成
type_dic = {1: '落葉広葉樹', 2: '常緑広葉樹', 3: '常緑針葉樹'}
tree_type = [1, 2, 1, 2, 2, 1, 1, 2, 3, 2, 1, 1, 2, 2, 1]
## 平均計算をしながらデータフレームを作成
# 測定本数・平均直径の算出 ※groupbyで和名単位の胸高直径のcountとmeanを計算
summary_df = (data_orgn.groupby(['和名'])['胸高直径'].agg(['count', 'mean'])
.set_axis(['測定本数', '平均直径(cm)'], axis=1))
# 平均樹高の算出 ※meltで縦持ち変換した後にgroupbyで和名単位の平均樹高を計算
tmp = (data_orgn[['和名', '樹高1', '樹高2', '樹高3', '樹高4']]
.melt(id_vars=['和名'], value_vars=['樹高1', '樹高2', '樹高3', '樹高4'],
var_name='測定回', value_name='平均樹高(m)')
.dropna()
.groupby(['和名'])[['平均樹高(m)']].mean())
# 各樹のタイプ(日本語)のデータフレーム化
tree_type_df = pd.DataFrame([type_dic[x] for x in tree_type],
index=summary_df.index, columns=['タイプ'])
# 3つのデータフレームを結合してデータフレームを最終化
summary_df = pd.concat([tree_type_df, summary_df, tmp], axis=1)
## データフレームの表示
display(summary_df.round(1))【実行結果】
各樹種ごとの測定本数は12~17本、平均直径・平均樹高はさまざまです。
平均樹高の値の一部はテキストと異なりますが、原因は不明です。

この平均値データを用いて、木の大きさを可視化しましょう。
棒グラフを描画します。
### 平均直径と平均樹高を棒グラフで描画
# 平均直径と平均樹高を昇順で並び替え
d_sorted = summary_df['平均直径(cm)'].sort_values()
h_sorted = summary_df['平均樹高(m)'].sort_values()
# 描画
fig, ax = plt.subplots(1, 2, figsize=(10, 4))
# 平均直径の棒グラフの描画
ax[0].bar(summary_df.index, d_sorted)
ax[0].xaxis.set_tick_params(rotation=60)
ax[0].set(title='平均直径', ylabel='平均直径(cm)')
# 平均樹高の棒グラフの描画
ax[1].bar(summary_df.index, h_sorted)
ax[1].xaxis.set_tick_params(rotation=60)
ax[1].set(title='平均樹高', ylabel='平均樹高(m)')
# 全体調整
plt.tight_layout()
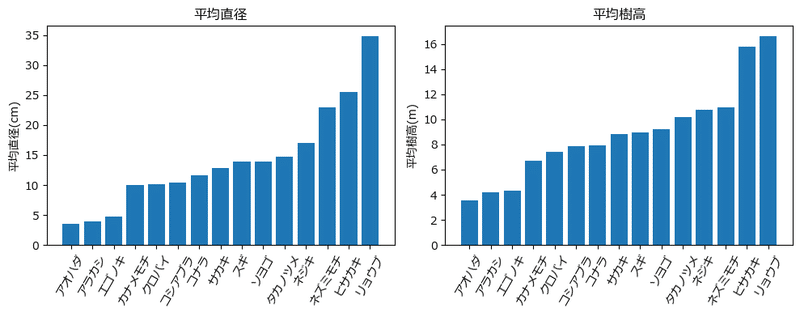
plt.show()【実行結果】
小さな値から並び替えました。
平均直径・平均樹高の並び順は同じです。
樹種間を比べると「直径が大きくなると樹高が高くなる」といった関係があるように見えます。

4.データの前処理
データ横持ちの測定回数ごとの樹高をモデルで扱いやすいように縦持ちに変換して、樹高データとします。
胸高直径データは1回しか測定されていないので、樹高データから独立したデータにします。
さらに、樹種の和名をラベルにしてインデックスを作成します。
### データの前処理
## data_orgnのインデックスを付加した一時データの作成
tmp = data_orgn.copy().reset_index(drop=False)
## 樹高データの作成
data_H = (tmp.melt(id_vars=['index', '和名', 'No', '胸高直径'],
value_vars=['樹高1', '樹高2', '樹高3', '樹高4'],
var_name='測定回', value_name='樹高')
.dropna().sort_values(['index', '和名', 'No', '測定回'])
.reset_index(drop=True))
print('【 樹高データ H 】')
display(data_H)
## 直径データの作成
data_D = tmp[['index', '和名', 'No', '胸高直径']].reset_index(drop=True)
print('【 直径データ D 】')
display(data_D)
## 樹高データの樹種インデックスの作成
species_idx, species_labels = pd.factorize(data_H['和名'], sort=True)
print('【 樹種 ラベルとインデックス】')
print(species_labels)
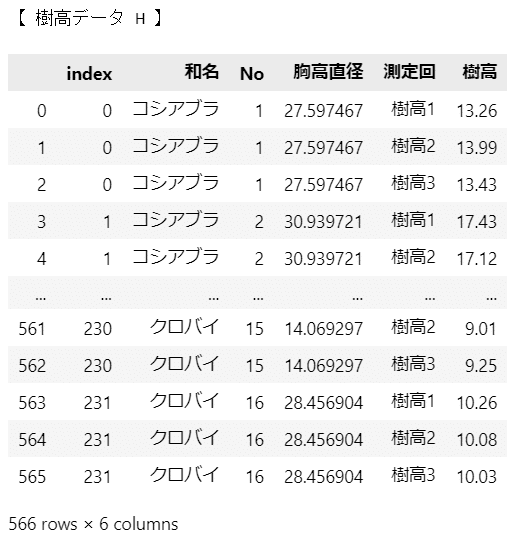
print(species_idx)【実行結果】
こちらは前処理後の樹高データです。
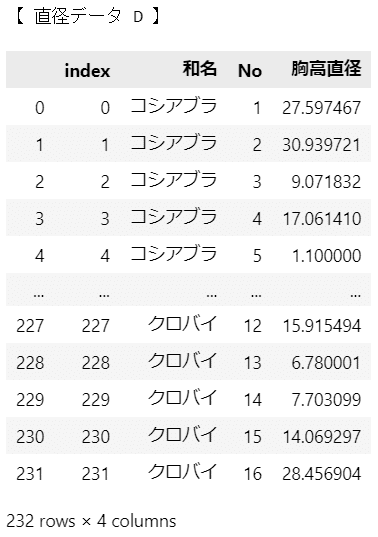
こちらは前処理後の直径データです。
こちらは樹種のラベルとインデックスです。
インデックスの数値は和名でソートされています。

モデル構築
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
$$
\begin{align*}
\sigma_{D},\sigma_{H}, \sigma_{\epsilon}, \sigma_{\epsilon_a},\sigma_{\epsilon_h},\sigma_{\epsilon_{H_{max}}} &\sim \text{HalfNormal}\ (\text{sigma}=10) \\
\\
\log \overline{a} &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=10)\\
\epsilon_a &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_{\epsilon_a})\\
a &\sim \exp(\log \overline{a} + \epsilon_a)\\
\\
\log \overline{h} &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=10)\\
\epsilon_h &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_{\epsilon_h})\\
h &\sim \exp(\log \overline{h} + \epsilon_h)\\
\\
\log \overline{H}_{max} &\sim \text{Normal}\ (\text{mu}=4,\ \text{sigma}=4)\\
\epsilon_{H_{max}} &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_{\epsilon_{H_{max}}})\\
H_{max} &\sim \exp(\log \overline{H}_{max} + \epsilon_{H_{max}})\\
\\
\overline{D} &\sim \text{HalfNormal}\ (\text{sigma}=100) \\
\epsilon &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_{\epsilon}) \\
\\
\log \overline{H} &= \log a + h \times \log \overline{D} + \log H_{max} - \log (a \times \overline{D}^h + H_{max}) + \epsilon \\
\\
likelihoodD &\sim \text{Normal}\ (\text{mu}=\overline{D},\ \text{sigma}=\sigma[D])\\
likelihoodH2 &\sim \text{Normal}\ (\text{mu}=\log\overline{H},\ \text{sigma}=\sigma[H])\\
\end{align*}
$$
1.モデルの定義
数式表現を実直にモデル記述します。
### モデルの定義
# 初期値設定
HD = 1.3 # 直径を測定した高さ
# モデルの定義
with pm.Model() as model:
### データ関連定義
## coordの定義
# 樹高データのインデックス
model.add_coord('dataH', values=data_H.index)
# 直径データのインデックス
model.add_coord('dataD', values=data_D.index)
# 樹種
model.add_coord('species', values=species_labels)
# パラメータのσの種類
model.add_coord('sigmaParam',
values=['D', 'H', 'epsilon', 'epsilona', 'epsilonh',
'epsilonHmax'])
## dataの定義
# 直径データ
D = pm.ConstantData('D', value=data_D['胸高直径'].values, dims='dataD')
# H2樹高データ(樹高H-直径を測定した高さHD)
H2 = pm.ConstantData('H2', value=data_H['樹高'].values - HD, dims='dataH')
# 樹種インデックス
speciesIdx = pm.ConstantData('speciesIdx', value=species_idx, dims='dataH')
# 直径データレファレンス(樹高データに持たせた直径データとのレファレンス)
refIdx = pm.ConstantData('refIdx', value=data_H['index'], dims='dataH')
### 事前分布
## 6つの標準偏差
sigmas = pm.HalfNormal('sigmas', sigma=10, dims='sigmaParam')
## パラメータa
# 平均
logabar = pm.Normal('logabar', mu=0, sigma=10)
# 変量効果
epsilona = pm.Normal('epsilona', mu=0, sigma=sigmas[3], dims='species')
# パラメータa
a = pm.Deterministic('a', pt.exp(logabar + epsilona), dims='species')
## パラメータh
# 平均
loghbar = pm.Normal('loghbar', mu=0, sigma=10)
# 変量効果
epsilonh = pm.Normal('epsilonh', mu=0, sigma=sigmas[4], dims='species')
# パラメータh
h = pm.Deterministic('h', pt.exp(loghbar + epsilonh), dims='species')
## パラメータHmax
# 平均
logHmaxbar = pm.Normal('logHmaxBar', mu=4, sigma=4)
# 変量効果
epsilonHmax = pm.Normal('epsilonHmax', mu=0, sigma=sigmas[5],
dims='species')
# パラメータHmax
Hmax = pm.Deterministic('Hmax', pt.exp(logHmaxbar + epsilonHmax),
dims='species')
## 真の直径Dbar
Dbar = pm.HalfNormal('Dbar', sigma=100, dims='dataD')
## logHbar
# 誤差
epsilon = pm.Normal('epsilon', mu=0, sigma=sigmas[2], dims='dataH')
# logHbar
logHbar = pm.Deterministic(
'logHbar',
(pt.log(a[speciesIdx])
+ h[speciesIdx] * pt.log(Dbar[refIdx])
+ pt.log(Hmax[speciesIdx])
- pt.log(a[speciesIdx] * pt.pow(Dbar[refIdx], h[speciesIdx])
+ Hmax[speciesIdx])
+ epsilon),
dims='dataH'
)
### 尤度
# 直径D
likeliD = pm.Normal('likeliD', mu=Dbar, sigma=sigmas[0],
observed=D, dims='dataD')
# 樹高H2:H-HD
likeliH2 = pm.LogNormal('likeliH2', mu=logHbar, sigma=sigmas[1],
observed=H2, dims='dataH')【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の4つを設定しました。樹高データの行の座標:名前「dataH」、値「行インデックス」
直径データの行の座標:名前「dataD」、値「行インデックス」
樹種の座標:名前「species」、値「樹種の和名」
$${\sigma}$$の座標:名前「sigmaParam」、値「$${\sigma}$$の添字含むパラメータの名前」
dataの定義
次の4つを設定しました。直径データ D
樹高から測定高さ1.3を引いたデータ H2
樹種インデックス speciesIdx
直径データレファレンス refIdx
(樹高データに持たせた直径データとのレファレンス)
パラメータの事前分布・計算値
テキストの記載のとおりです。
尤度
直径 D は正規分布、樹高-1.3 H2 は対数正規分布に従うとしています。
2.モデルの外観の確認
# モデルの表示
model【実行結果】
パラメータが多いのでたくさんの数式が並びます。

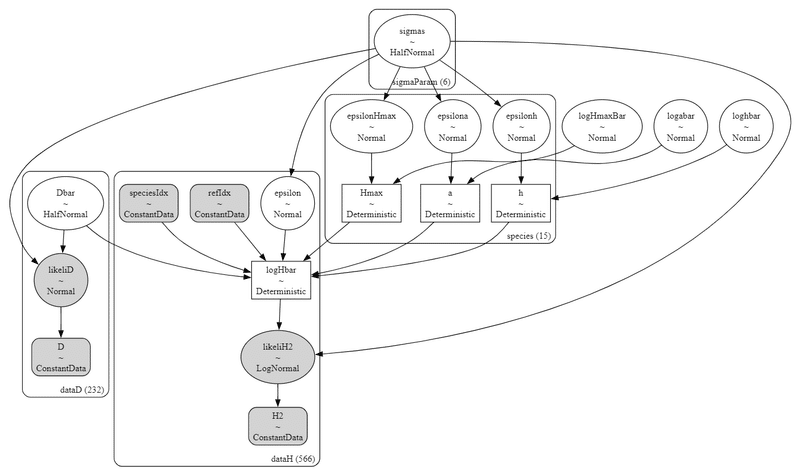
# モデルの可視化
pm.model_to_graphviz(model)【実行結果】
標準偏差がヘッドで仕切っているみたいな構図、面白いですねw

3.事後分布からのサンプリング
テキストにならって、パラメータの初期値を設定してみます。
右側に「#コメント」のあるパラメータのデータ型を整えることに、たいへん苦労しました(なかなかエラーが消えなくて)。
### MCMCの初期値の設定
# numpyの乱数生成器の生成
rng = np.random.default_rng(seed=1234)
# パラメータの初期値設定:乱数生成器で発生させた乱数を初期値にする
initvals = {
'Dbar': rng.uniform(low=10, high=50, size=len(data_D)).tolist(), # リスト
'logHmaxBar': rng.normal(loc=4, scale=2, size=1)[0], # スカラー
'logabar': rng.standard_normal(size=1)[0], # スカラー
'loghbar': rng.standard_normal(size=1)[0], # スカラー
'epsilona': rng.standard_normal(size=len(species_labels)),
'epsilonh': rng.standard_normal(size=len(species_labels)),
'epsilonHmax': rng.standard_normal(size=len(species_labels)),
'epsilon': rng.standard_normal(len(data_H)),
'sigmas': rng.uniform(low=0, high=1, size=6),
}続いてMCMCの実行です。
乱数生成数はテキストと同じです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ13分でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 12分50秒
# テキスト:iter=6000, warmup=3000, chains=デフォルト(おそらく4)
with model:
idata = pm.sample(draws=3000, tune=3000, chains=4,
target_accept=0.999,
nuts={'max_treedepth': 12},
initvals=initvals,
nuts_sampler='numpyro', random_seed=1234)【実行結果】

4.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$とします。
### r_hat>1.1の確認
# 設定
idata_in = idata # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
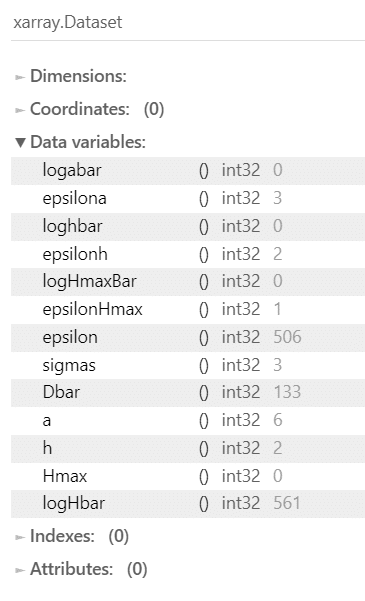
(az.rhat(idata_in) > threshold).sum()【実行結果】
$${\hat{R} > 1.1}$$のパラメータが多数存在します。
収束条件を満たすことができませんでした。
収束できていない推論データでは分析に使えません(泣)
そこで、ここからは、一般的な推論データ確認と、分析には使えませんがテキストのコードをPython化して動かしてみます。
手始めにざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
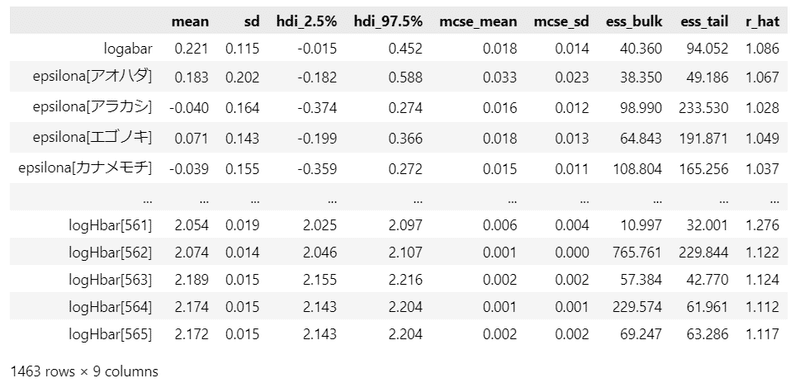
### 推論データの要約統計情報の表示
pm.summary(idata, hdi_prob=0.95, round_to=3)【実行結果】
$${\hat{R}}$$を見ますと、収束まであと一息な感じがします。
注目するパラメータに限定して要約統計量を確認しましょう。
$${\sigma}$$と$${H_{max}}$$から。
指数表示(1+5eみたいなもの)を回避するために、小数点第3位を固定化します。
### 推論データの事後統計量の表示 σ、Hmax
# 指数表示の無効化(小数点第3位固定化)
pd.options.display.float_format = '{:.3f}'.format
# 事後統計量の表示
var_names = ['sigmas', 'Hmax']
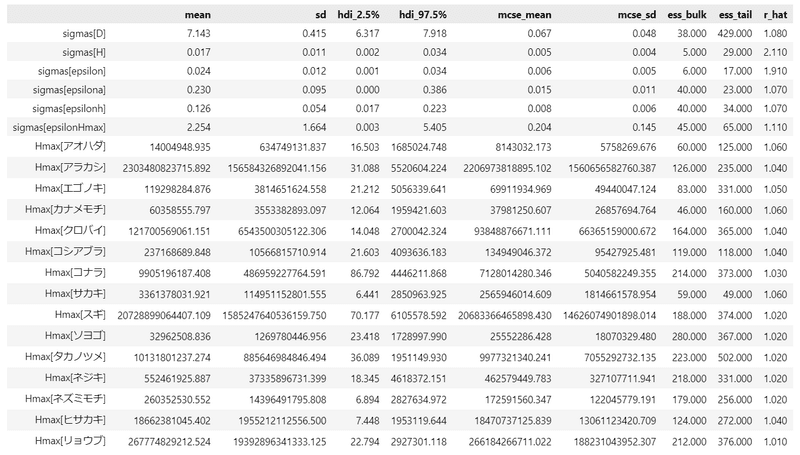
pm.summary(idata, hdi_prob=0.95, var_names=var_names)【実行結果】
テキストと照らし合わせてみます。
樹高の測定誤差のばらつき$${\sigma_H}$$の事後平均は、テキストは$${0.03}$$、こちらは$${0.017}$$。近似しています。
直径の測定誤差の標準偏差$${\sigma_D}$$の事後平均は、テキストは$${0.52cm}$$、こちらは$${7.143cm}$$。ずいぶんと乖離してしまいました。
そして何よりも残念なのは、樹高の潜在的な最大値$${H_{max}}$$です。
スギの事後平均は20兆mです!ありえない!
桁外れに外れています。自己流PyMCモデルのどこかがおかしいのでしょう。
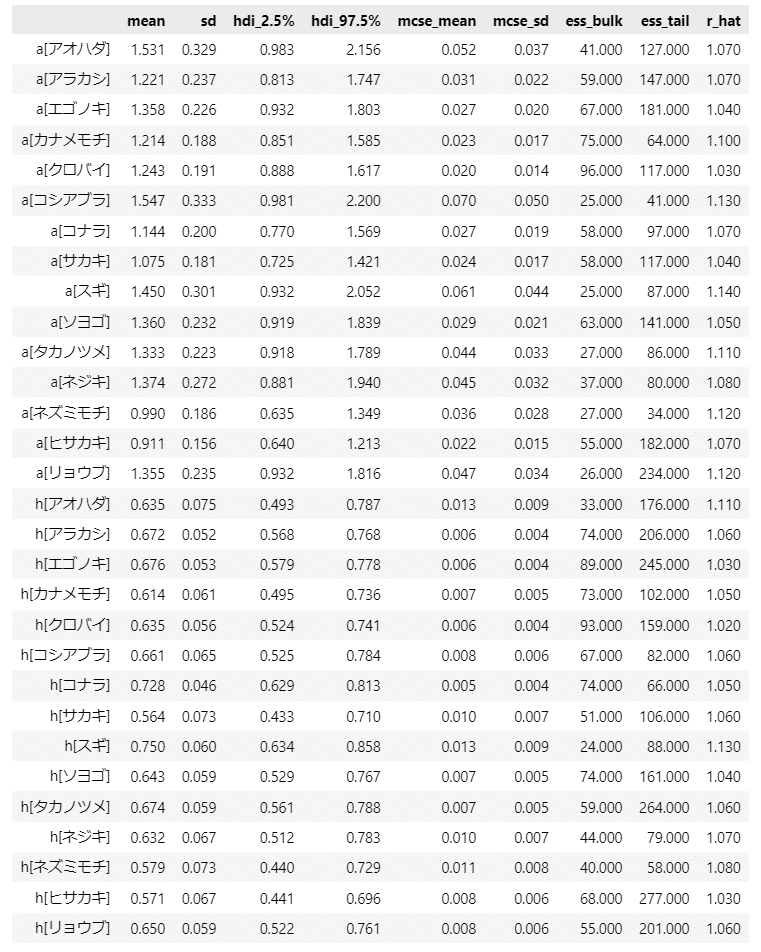
パラメータ$${a,h}$$を見ましょう。
### 推論データの事後統計量の表示 a、h
var_names = ['a', 'h']
pm.summary(idata, hdi_prob=0.95, var_names=var_names)【実行結果】
事後平均値や標準偏差の妥当性はよく分かりません。
こちらのコードは小数点第3位の固定化を解除するものです。
# 指数表示の無効化の解除(小数点第3位固定化の解除)
pd.options.display.float_format = None続いてトレースプロットを確認しましょう。
### トレースプロットの表示
pm.plot_trace(idata, compact=True)
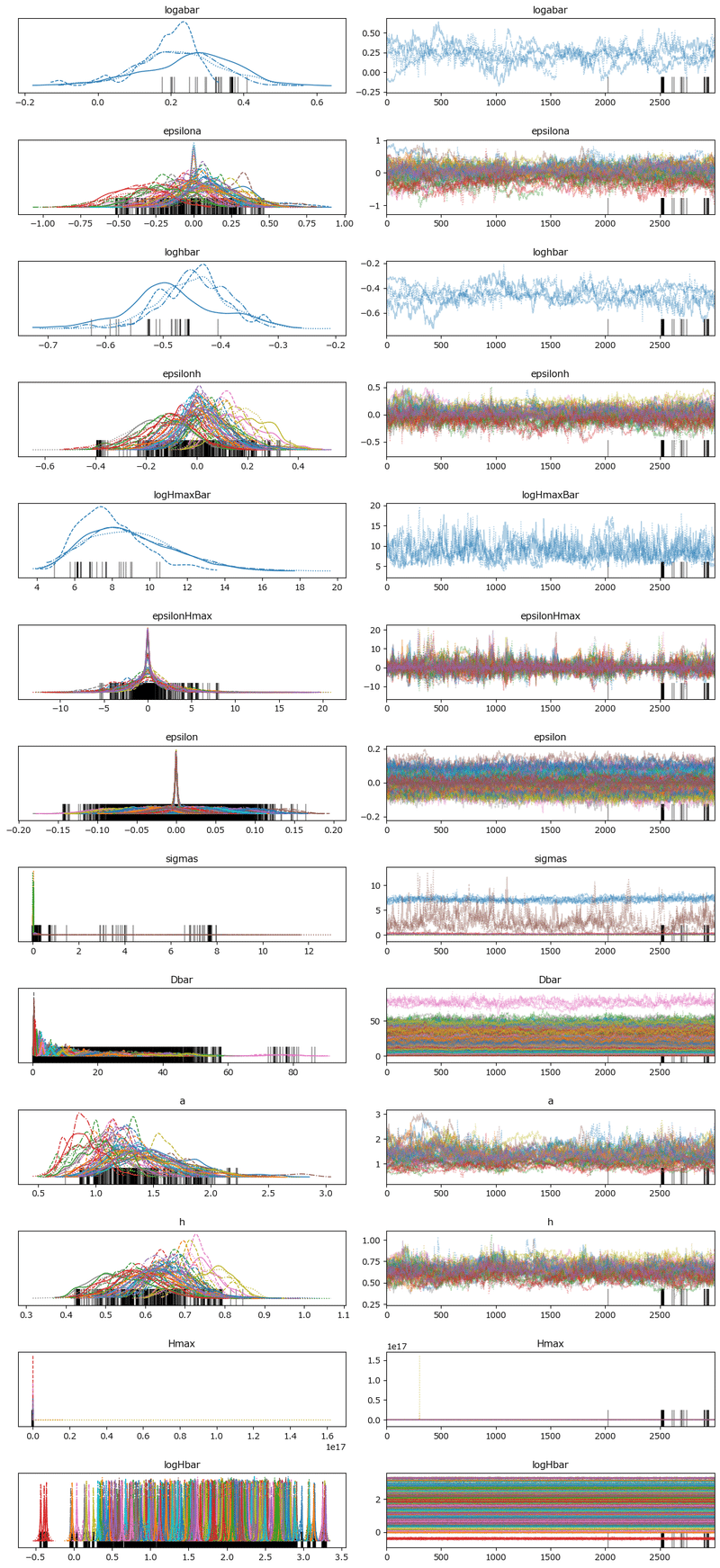
plt.tight_layout();【実行結果】
左のグラフには4本のマルコフ連鎖chainがばらばらに分布しているパラメータがあります。
右のグラフにはまんべんなく線が描画されていないパラメータがあります。
グラフ下部には発散を示すバーコードが多数散見されます。
収束していません(汗)

分析のようなもの
テキストの図5.3で示されるような樹種ごとの直径と高さの関係の可視化を行ってみます。
推論データは収束していませんので、あくまでコード作成&可視化のイメージ作りにご利用くださいませ。
まず、直径Dが0.1~65cmのときの樹高の推定値(中央値、95%CI)を計算します。
複雑に見えますが、ベイズモデリングの数式に則っているので、「テキストのモデリング」項の数式を参照しながらコードを確認するのが良いと思います。
### 図5.3描画のための各種値算出
## 樹高計算関数の定義
def calc_height(D, a, h, H_max, H_D):
return a * D**h * H_max / (a * D**h + H_max) + H_D
## 事後分布サンプリングデータをパラメータごとに抽出
# 次元なし
log_H_max_bar = idata.posterior.logHmaxBar.stack(sample=('chain', 'draw')).data
log_a_bar = idata.posterior.logabar.stack(sample=('chain', 'draw')).data
log_h_bar = idata.posterior.loghbar.stack(sample=('chain', 'draw')).data
# 樹種次元あり
epsilon_H_max = idata.posterior.epsilonHmax.stack(sample=('chain', 'draw')).data
epsilon_a = idata.posterior.epsilona.stack(sample=('chain', 'draw')).data
epsilon_h = idata.posterior.epsilonh.stack(sample=('chain', 'draw')).data
## 樹高計算のパラメータ値の算出
# パラメータ値
H_max = np.exp(np.tile(log_H_max_bar, (len(species_labels), 1)) + epsilon_H_max)
a = np.exp(np.tile(log_a_bar, (len(species_labels), 1)) + epsilon_a)
h = np.exp(np.tile(log_h_bar, (len(species_labels), 1)) + epsilon_h)
# x軸の直径値
D = np.linspace(0.1, 65, 101)
## 樹高の算出
heights = []
for i in range(len(species_labels)):
height = []
for d in D:
height.append(calc_height(d, a[i], h[i], H_max[i], 1.3))
heights.append(height)
heights = np.array(heights)
## 樹高の中央値と95%CI区間の算出
med = np.median(heights, axis=2)
ci_lower, ci_upper = np.quantile(heights, q=(0.025, 0.975), axis=2)
## 樹高の観測値の樹単位の平均値の算出
data_H_mean = data_H.pivot_table(index=['和名', 'No', '胸高直径'], values='樹高',
aggfunc='mean', sort=False).reset_index()
【実行結果】なし
描画しましょう。
観測値の散布図、樹高推論値の中央値の折れ線グラフ、95%CIの塗りつぶしを行っています。
### 推論値を用いた直径と高さの関係の描画 ※図5.3に相当
# 描画領域の指定
fig, ax = plt.subplots(5, 3, figsize=(12, 15), sharey=True)
# 樹種ごとに描画処理を繰り返す
for i, tree in enumerate(species_labels):
# axesの位置を指定
j = divmod(i, 3)
# 樹ごとの直径・高さの観測値の描画(高さは平均値)
ax[j].scatter(data_D[data_D['和名']==tree]['胸高直径'],
data_H_mean[data_H_mean['和名']==tree]['樹高'],
alpha=0.5)
# 事後中央値の描画
ax[j].plot(D, med[i], color='blue')
# 事後95%CI区間の描画
ax[j].fill_between(D, ci_lower[i], ci_upper[i], color='tomato', alpha=0.3)
# 修飾
ax[j].set(title=f'{species_labels[i]}')
ax[j].grid(lw=0.5)
# 全体修飾
fig.supxlabel('直径(cm)')
fig.supylabel('高さ(m)')
plt.tight_layout();【実行結果】
青点が観測値、青線が推論値の中央値、赤塗りが推論値の95%CIです。
なんとなくですが、それっぽい図になりました。
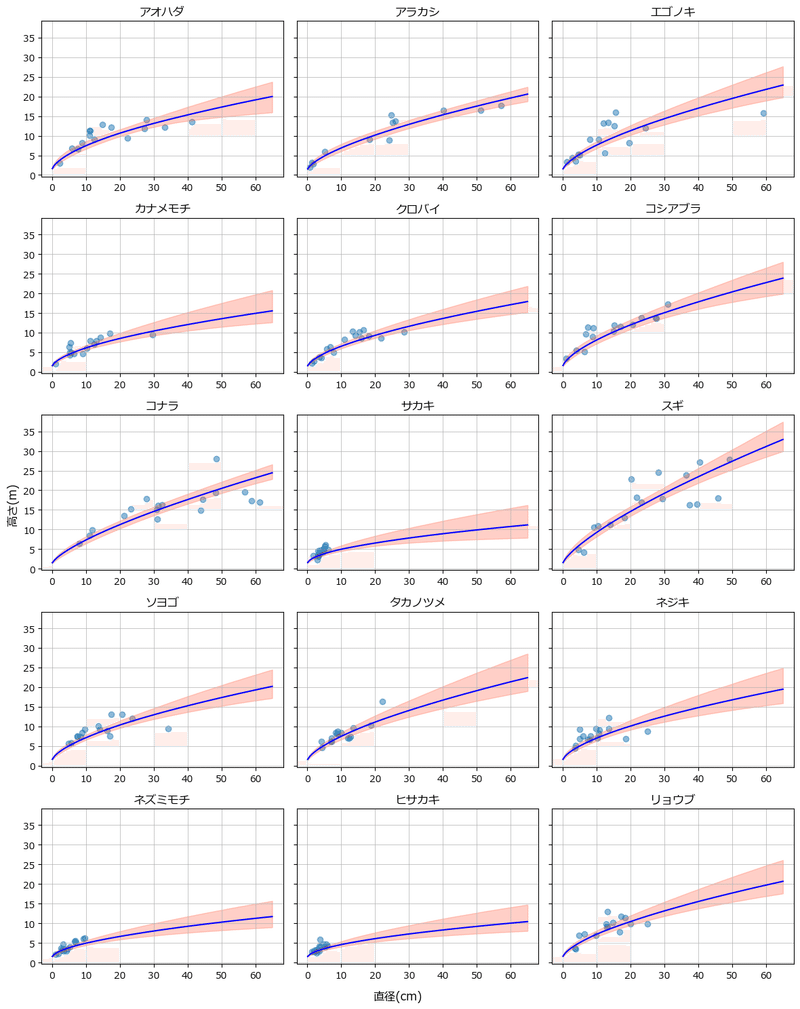
テキスト掲載の「カナメモチ」と「コナラ」に関しては、推論値がやや高めになっています。
テキストでは、カナメモチの中央値の最大が12m程度ですが、このグラフでは15mになっています。
コナラの中央値の最大は、テキストは20m弱、このグラフは25mです。

【まとめ】
今回の推論データを使うことはあまり推奨できませんが、こうして、推論したパラメータのサンプリングデータを用いて、モデルの数式に当てはめて、目的変数である「樹高」を推論値を計算できました。
ベイズのMCMCサンプリングデータの活用方法をまた1つ学ぶことができました。
最後に、推論データを再利用する(かもしれない)場合に備えてファイルに保存しましょう。
idataをpickleで保存します。
### idataの保存 pickle
file = r'idata_ch05.pkl'
with open(file, 'wb') as f:
pickle.dump(idata, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata_ch05.pkl'
with open(file, 'rb') as f:
idata_load = pickle.load(f)以上で第5章は終了です。
おわりに
予測
今回の「木の高さを推論するモデル」には、機械学習に通じるものを感じました。
観測データの「説明」・「メカニズムの把握」にとどまることなく、未知データの「予測」に用いる目的を持っているからです。
直径と樹高の観測データからモデルを構築して(train)
未知の木の直径データをモデルに与えて樹高を予測する(predict)
予測に寄与するベイズモデルを自在に構築できる「ベイズ使い」になりたいです。

シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
