見出し画像
Photo by yesyoshino

シリーズPython③ 異常検知にチャレンジ

ネイピア DS

はじめに

雑誌記事「Python × 数学ブートキャンプ」の紹介

Software Design 誌 2023年5月号の特集「Python × 数学ブートキャンプ」（以下、テキストと呼びます）の記事はとても有意義でした。
データサイエンスの基礎となる数学の初歩的な部分をPythonコードを交えて学ぶことができるおすすめのテキストです。

テキストの課題

ただし、Pythonコードについて、コードの一部が省略されていて、テキストのコードを写経してもうまく動かない場面もありました。

この記事の目標

この記事は、省略されたコードを補完して動くコードにすることを目標にして書きました。
テキストの記事のうち「COLUMN 異常検知にチャレンジ」を対象にしています。

お断り

この記事は投稿当初の内容から変更されています。

実は、編集ミスにより、記事を変更保存してしまったのでした。。。
別の記事を執筆する際に、この記事を複製して作成したつもりでした。
しかし実際には、別の記事を上書きして保存してしまい、結果として、投稿当初の記事は失われてしまいました（泣）

この記事の再作成は、JupyterNotebook に記録済みの文章に基づいて行いました。

まえがき

このNotebook風記事は、出典に記載の雑誌（以下「テキスト」と呼ぶ）に掲載された記事及びコードを引用し、適宜、掲載文章を改変し、掲載コードの過不足を変更しています。

テキストに未掲載のコード部分については、「あくまで想像に基づく処理内容」に基づいて書いており、処理の正確性は担保しておりません。

なお、テキストに未掲載のコード部分については、「あくまで想像に基づく処理内容」に基づいて書いており、処理の正確性は担保しておりません。誤りや改善点がありましたら、ぜひ教えてください。

【出典】
Software Design 2023年5月号 Special Feature 1「Python×数学ブートキャンプ」COLUMN 異常検知にチャレンジ

ホテリングのT2法による異常検知の概要

ホテリングのT2法とは

  • ホテリングの$${T^2}$$法は教師なしの異常検知手法です。

異常度

  • データの異常度$${a(x')}$$を次の数式で求めます。
    $${a(x')=(x'-\mu)^T \Sigma^{-1} (x'-\mu)}$$

  • データ$${x'}$$とその平均$${\mu}$$の乖離度合いをデータの分散$${\Sigma}$$を考慮して計算しています。
    なお、異常度$${a(x')}$$はマハラノビス距離$${d(x,y)=\sqrt{(x-\bar{x})^T\Sigma^{-1}(y-\bar{y})}}$$の２乗と対応しています。

閾値と確率分布

  • ホテリングの$${T^2}$$法では、異常度が閾値を超えたら「異常である」と判定します。

  • 閾値にはカイ二乗分布を想定します。
    具体的には「データ数が項目数（$${M}$$）より大きい場合において自由度$${M}$$のカイ二乗分布に近似的に従うこと」を利用します。

異常検知の実装

インポート

import numpy as np
from scipy.stats import chi2
from scipy.spatial import distance
import matplotlib.pyplot as plt

シミュレーション用データの作成（図Aに対応）

  • ３つのセンサーが１秒毎に記録する1000秒間のログデータを想定して正規分布の乱数を生成します。

  • 800秒以降が故障状態であり、sensor1にノイズを加算しています。

# シミュレーション用データの作成関数
def synthetic_sensor_data(num_sensors, num_examples):
    mean = np.array([(i+1)*15 for i in range(num_sensors)])
    cov = np.ones((num_sensors, num_sensors)) * 0.5
    cov += np.identity(num_sensors) * 0.5
    X = np.random.multivariate_normal(mean, cov, num_examples)
    interval = 800
    X[interval:, 1] += np.random.normal(loc=2, scale=1, size=len(X)-interval)
    return X, mean, cov

# シミュレーション用データの作成（1000行、3列のnumpy配列）
np.random.seed(1)
data, mu, cov_mtx = synthetic_sensor_data(3, 1000)

# データの概要
print('dataの形状: ', data.shape)
print('【乱数を生成した正規分布の情報】')
for i in range(3):
    print(f'sensor{i}: 平均: {mu[i]}, 分散共分散: {cov_mtx[i]}')
出力イメージ

シミュレーション用データの描画（図Bに対応）

  • dataを単純に折れ線グラフにプロットします。

  • sensor1の800秒以降に乱れが含まれています。

x = np.arange(0, 1000)
for i in range(3): 
    plt.plot(x, data[:, i], lw=0.5, label=f'sensor {i}')
plt.xlabel('time-series data of sensors')
plt.ylabel('value')
plt.legend(loc='upper left')
plt.show()
出力イメージ

カイ二乗分布の可視化（図Cに対応）

  • 異常度の閾値に用いる「自由度3のカイ二乗分布の確率密度関数」を可視化します。

  • 閾値（threshold）をカイ二乗分布の上側確率が0.5%になる点に設定します。
    赤い線が確率0.5%以上の領域（閾値12.8）です。

# 設定：閾値用の確率、自由度
prob= 0.005
df = 3

# 閾値の取得：上側確率0.5%点
threshold = chi2.ppf(1-prob, df=df)
# Normal域のカイ二乗分布の確率密度関数の取得
x1 = np.linspace(0, threshold, 1000)
y1 = chi2.pdf(x1, df=df)
# Anormaly域のカイ二乗分布の確率密度関数の取得
x2 = np.linspace(threshold, 20, 100)
y2 = chi2.pdf(x2, df=df)

# プロット
plt.plot(x1, y1, lw=1, color='steelblue', label='Normal')
plt.plot(x2, y2, lw=2, color='red', label=f'Anormaly: {threshold:.1f}')
# 修飾
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.title(f'$\chi^2({df})$')
plt.legend()
plt.show()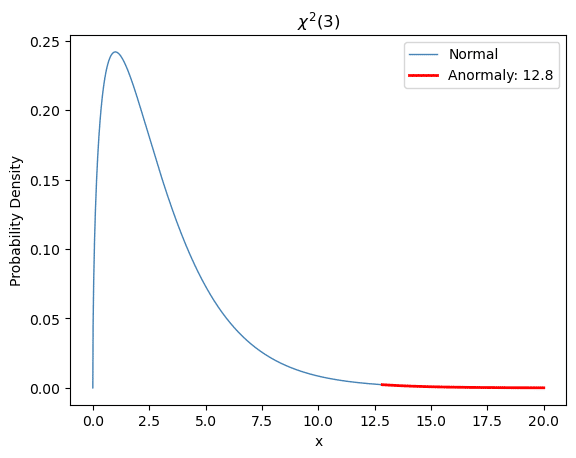
出力イメージ

異常検知処理の実行（図Dに対応）

  • モデルのトレーニング（マハラノビス距離の計算に必要な分散$${\Sigma}$$の逆行列を算出）は500秒までのシミュレーション用データで実施しています。

  • 異常と判定するアラートの閾値は、前述のコードで算定した12.8にしています（自由度3のカイ二乗分布の上側確率0.5%点）。

  • テキストによると「正規分布の次元数がデータ数より十分に大きい場合、マハラノビス距離の2乗は自由度3のカイ二乗分布で近似できることが分かっている」とのことです。

# トレーニング：分散共分散行列の逆行列を取得
training_data = data[:500].copy()
cov_inv = np.linalg.pinv(np.cov(training_data.T)) # 分散共分散行列の逆行列を計算

# T2スコアの算出（異常度a(x')の算出）
T2 = []
for i in range(len(data)):
    t2_score = distance.mahalanobis(data[i, :], data.mean(axis=0), cov_inv)**2
    T2.append(t2_score)

# プロット（閾値は自由度3のカイ二乗分布の上側確率0.05%点）
x = np.arange(len(T2))
plt.plot(x, T2, color='steelblue', lw=0.5, label='$T^2$ score') # T2スコアのプロット
plt.axhline(threshold, color='red', label='threshold')          # 閾値水準のプロット
plt.legend()
plt.show()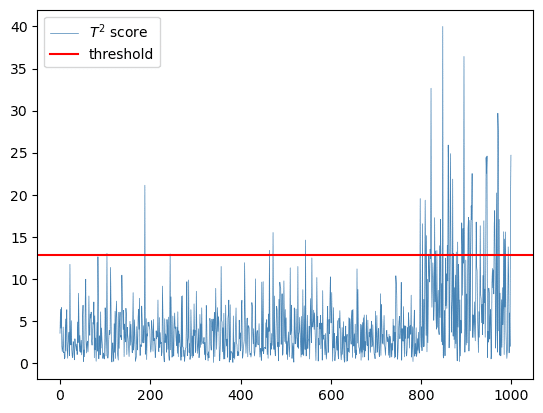
出力イメージ

参考サイト
テキスト掲載の参考サイトのURLを添えておきます

結び

初めて異常検知タスクに取り組みました。
「テキスト」のおかげです。ありがとうございました。
確率分布と機械学習が結びつくこの手法のおかげで、統計の学びの楽しさがまたまた倍増いたしました。
これからも異常検知タスクに注目したいと思います。

【お願い】
ところで、テキストのコードのラスボスをまだ攻略できていません。
それは「ナイーブベイズ」。
テキスト31ページの「図17 ナイーブベイズモデルの実装例」「図18 ナイーブベイズモデルの利用例」の完全なコードをお持ちの方、ぜひ共有してください。
お願いいたします。

おわり

ブログの紹介

noteで２つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計
統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。

２．Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

いいなと思ったら応援しよう！