
第9回 これだけ!行列式の使い道。講座の目指すところ(線形代数)
前回は行と列の基本変形を用いた行列式計算方法について解説しました。
前回の最後で「次回はなんで行列式を解く必要があるのか、その活用法の一端にふれましょう。」と宣言した手前、どのように説明するか悩んでいましたが、この際私たちが目指すところを洗いざらい話しちゃえ、ということで、線形代数の講座の最終的な到達点をお伝えしたうえで、行列式が何に使われているか、この先何を学ぶ必要があるのかを、紹介しましょう。
なお今回は高校物理の内容が出てきます。なるべくわかりやすく説明するつもりですが、ぜひ復習をお勧めします。
1.本題に入る前に物理の復習
皆さん、単振動って覚えてますか?単振動とは、
量の時間変化が三角関数の正弦関数または余弦関数で表される振動である。調和振動(ちょうわしんどう)や、単調和振動、調和運動とも呼ばれる。
とのことです。次のような質量$${m}$$の質点にバネ定数$${k}$$のバネが繋がった系(ばねマス系)を考えます。
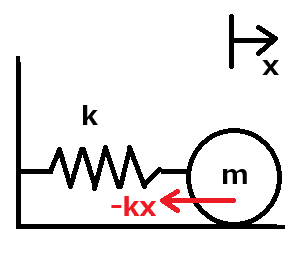
ここで質点が動くとバネは質点の移動を妨げる方向に力を及ぼします。これをフックの法則と呼びましたね。式にすると以下になります。
$$
F=-kx
$$
一方、物体にはニュートンの運動法則が適用されます。その中の第二法則は次のように定義されます。
質点の加速度$${a}$$は、そのときの質点に作用する力$${F}$$に比例し、質点の質量$${m}$$に反比例する。
この法則を式に表すと次のようになります。
$$
F=ma
$$
以上の2式を連立して運動方程式をたてると、
$$
ma+kx=0
$$
$${a=\"{x}}$$から、
$$
m\"{x}+kx=0
$$
このように$${x}$$についての微分方程式が完成します。
これをごにょごにょ解くことで(解き方はここでは省略します)、
$$
x=A\cos(\omega t+\phi)
$$
と求まるのでした。このように1質点系は高校数学・高校物理の範囲で簡単に求めることができます。1質点系は。
2.問題提起。私たちが学ぶべきこと
では質点を2つに増やしたらどうなるでしょうか。

1質点系と同様に運動方程式をたてると、
$$
m\"{x_{1}}=-k_{1}x_{1}+k_{3}(x_{2}-x_{1})=-(k_{1}+k_{3})x_{1}+k_{3}x_{2}\\
m\"{x_{2}}=-k_{2}x_{2}+k_{3}(x_{1}-x_{2})=-(k_{2}+k_{3})x_{2}+k_{3}x_{1}
$$
これを整理すると、
$$
\"{x_{1}}=-\frac{(k_{1}+k_{3})}{m}x_{1}+\frac{k_{3}}{m}x_{2}\\
\"{x_{2}}=-\frac{(k_{2}+k_{3})}{m}x_{2}+\frac{k_{3}}{m}x_{1}
$$
これを行列式で表すと、次で表されます。
$$
\"{X}=-AX\\
A=
\begin{bmatrix}
\frac{(k_{1}+k_{3})}{m}&-\frac{k_{3}}{m}\\
-\frac{k_{3}}{m}&\frac{(k_{2}+k_{3})}{m}
\end{bmatrix}\quad
X=
\begin{bmatrix}
x_{1}\\
x_{2}
\end{bmatrix}
$$
と求まります。問題はここからです。では具体的に$${x_{1},x_{2}}$$を求めてくださいとなります。しかし質点の加速度はお互いの変位に影響を受けて複雑に変化し、その加速度によって変位が変化するとまた加速度がお互いの質点に影響を及ぼし合って変化するという、非常に複雑な関係となっており、解くのムズくね?となるわけです。
しかし工学とは、基礎科学を工業に応用する学問であり、人々にとって実用的な工業製品を生み出すためには、まず自然現象を正しく理解することが不可欠です。どんなに難しくても解かなければなりません。この講座では「工学系の論文を読み、内容を理解できるようになる」ことを目的として知識の提供をしていますが、そういった論文でよく行われる「自然現象の数式化」「自然現象の理解」をせめて簡単なものでも自力でできるようにしようというわけです。
3.どうすれば、何を学べば解けるのか
以下の式のままでは到底解けないことが分かりました。ではどのような式の形であれば解けるでしょうか?
$$
\"{X}=-AX\\
A=
\begin{bmatrix}
\frac{(k_{1}+k_{3})}{m}&-\frac{k_{3}}{m}\\
-\frac{k_{3}}{m}&\frac{(k_{2}+k_{3})}{m}
\end{bmatrix}\quad
X=
\begin{bmatrix}
x_{1}\\
x_{2}
\end{bmatrix}
$$
答えは下に示すような式の形です。
$$
\"{Q}=-\Lambda Q\\
\Lambda=
\begin{bmatrix}
a&0\\
0&b
\end{bmatrix}\quad
Q=
\begin{bmatrix}
q_{1}\\
q_{2}
\end{bmatrix}
$$
このように$${\Lambda}$$のような対角行列で表現することができれば、
$$
\"{q_{1}}+aq_{1}=0\\
\"{q_{2}}+bq_{2}=0
$$
となり、お互いの座標軸に影響を及ぼし合わない、単独の形で運動を記述することができます。これなら前の節の単振動と同じ要領で解くことができますね。
実際どうやって解くかというと、次のような線形変換を行います。
$$
UQ=X
$$
線形変換、聞きなれない言葉が出てきましたね。
とにかく行列$${U}$$を用いて上式のように空間を変形させることで、
$$
\"{Q}=-\Lambda Q
$$
という運動方程式が導かれます。この時$${\Lambda}$$は実は次のように求まります。
$$
U^T AU=\Lambda
$$
これを「行列$${A}$$の対角化」などといいます。
そして線形変換とやらで出てきた$${U}$$って何?と疑問に思うもしれませんが、これは行列$${\bold A}$$の固有ベクトルを列成分とした行列です。
「????」となっているかと思いますがもう少し我慢してください!
固有ベクトルとやらは行列$${A}$$から求まります。具体的には以下の式から求まります。
$$
AX=\lambda X
$$
この式を満たす$${X}$$が固有ベクトルです。上の式を固有方程式といいます。そして固有方程式を満たすときの$${\lambda}$$を固有値と呼び、固有ベクトルを求めるにはまずこの固有値を求める必要があります。
具体的にどうやって求めるかというと、この固有方程式は次式のように変形されます。
$$
\begin{pmatrix}
A-\lambda I
\end{pmatrix}
X=0
$$
この方程式が$${X=0}$$以外の解を持つための条件は
$$
\begin{vmatrix}
A-\lambda I
\end{vmatrix}
=0
$$
となります。よってこの行列式を$${\lambda}$$について解くことで固有値が求まり、固有ベクトルが求まり、行列$${U}$$が求まり、対角行列$${\Lambda}$$が求まり、$${Q}$$が求まり、最後に求めたかった$${X}$$が求まるわけです。つまり、行列式は物理現象を数式化する上では最も末端に位置する計算であり、それゆえ最も基本的で重要な計算と言えます。工学分野の研究では毎日のようにこの行列式とにらめっこすることになるので、今のうちに計算に慣れておきましょうね。
最後に物理現象の数式化の考え方についておさらいしましょう。
物理現象を説明する微分方程式をうちたてる(この講座ではこちらが用意します)
↓
微分方程式が解きやすい形になるように、つまり微分方程式を支配する行列を①対角化するために微分方程式を②線形変換したい。
↓
線形変換するためには微分方程式を支配する行列の③固有ベクトルを求める必要がある。
↓
固有ベクトルを求めるためには、微分方程式を支配する行列の④固有値を求める必要がある。
↓
固有値を求めるためには微分方程式を支配する行列についての⑤固有方程式を解く必要がある。
↓
固有方程式を解いて固有値を求めるために行列式を解く必要がある。
こういう考え方をするわけです。
したがって「自然現象の数式化」「自然現象の理解」をせめて簡単なものでも自力でできるようにするためにも、まだ説明していない①~⑤の項目についてこれから頑張って解説していきます。
まとめ
今回は線形代数の講座の最終的な到達点と、行列式が何に使われているか、そしてこの先何を学ぶ必要があるのかをお伝えしました。今はフーンくらいで聞いてもらえれば大丈夫です。少しづつ理解していきましょう。
このブログは理工系として必要最低限の会話ができる知識をお伝えしていますが、書籍と合わせて勉強することでより効率的にそしてさらに深く勉強が進むかと思います。まずこちらの書籍を手に取ってみて、並行して学んでみるのもいいかもしれません。
次回は線形変換についてです。次はこちら↓
この記事が気に入ったらサポートをしてみませんか?
