
(追記有り)中学でも分かるガロアの証明➂『剰余類』及び『正規部分群』について
ここでは剰余類、及び正規部分群について解説をします。この考えは、「5次以上の方程式に解の公式が存在しない」ことを証明する上での重要なアイデアです。
置換の積に関して、3次対称群
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
の部分群には、全部で以下の6通りがあります(本シリーズ (29))。
$${\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}=S_3}$$
$${\{id, \rho_2, \rho_3\}=A_3}$$
$${\{id, \tau_1\}}$$
$${\{id, \tau_2\}}$$
$${\{id, \tau_3\}}$$
$${\{id\}}$$
$${A_3}$$ は遇置換のみからなる部分群で、3次交代群とよばれます。(群であるので当然ですが)これらはすべて、以下の群の定義を満たします。
群の定義(復習)
空でない集合 $${G}$$ の任意の要素 $${a, b, c}$$ の間に1つの演算 $${*}$$ が規定されているとする。
この集合 $${G}$$ の任意の要素 $${a, b, c}$$ が、その演算 $${*}$$ に関して次の条件を満たすとき、$${G}$$ は演算 $${*}$$ に関して群であるという。
(1) $${a*b}$$ は $${G}$$ の要素である。
(2) 交換法則 $${(a*b)*c=a*(b*c)}$$ が成り立つ。
(3) $${a*e=e*a=a}$$ となる単位元 $${e}$$ が $${G}$$ に存在する。
(4) $${a*x=x*a=e}$$ となる逆元 $${x}$$ が $${G}$$ に存在する。
***
(1) を満たすことを、集合 $${\bm G}$$ は演算 $${\bm *}$$ について閉じているといいます。演算の結果、集合 $${G}$$ からはみ出さないことを意味します。
(2) は、カッコを気にしないで、どこから演算を施してもよいことを保証します。
(3) は、左右どちらから演算を施しても変化しない要素の存在です。その要素を単位元といいます。
(4) は、左右両方から演算を施すと単位元となる要素の存在です。その要素を逆元といいます。
要するに群とは、イメージとして
(1) 全部そろっている
(2) つなげることができる
(3) 変えないことができる
(4) 元に戻すことができる
の4つの条件が成り立つ要素の集まり(集合)です。
部分群の「置換の積」の演算表
部分群について補足していきます。部分群
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
について、置換の積の演算表は次の様になります(本シリーズ(28))。
$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c|c|c|c}
& id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3\\ \hline\hline
id & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3\\ \hline
\rho_2 & \rho_2 & \rho_3 & id & \tau_3 & \tau_1 & \tau_2\\ \hline
\rho_3 & \rho_3 & id & \rho_2& \tau_2 & \tau_3 & \tau_1\\ \hline
\tau_1 & \tau_1 & \tau_2 & \tau_3 & id & \rho_2 & \rho_3\\ \hline
\tau_2 & \tau_2 & \tau_3 & \tau_1 & \rho_3 & id & \rho_2\\ \hline
\tau_3 & \tau_3 & \tau_1 & \tau_2 & \rho_2 & \rho_3 & id
\end{array}
$$
得られる $${6\times6=36}$$ 通りの結果は、すべて $${S_3}$$ の要素になっているので、$${S_3}$$ は置換の積について閉じていることがわかります。
また、どの縦の1列をみても、どの横の1列をみても $${S_3}$$ の要素がすべて出そろっており、一般にこれは群の性質となります(証明は割愛)。
置換の積は可換ではないこと
ここで、置換の積の順序を入れ替えると、必ずしも同じにならないことに注意しましょう。例えば
$${\rho_2\rho_3=id}$$(下線部)
$${\rho_3\rho_2=id}$$(波線部)
$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c|c|c|c}
& id & \utilde{\rho_2} & \underline{\rho_3} & \tau_1 & \tau_2 & \tau_3\\ \hline\hline
id & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3\\ \hline
\underline{\rho_2} & \rho_2 & \rho_3 & \underline{id} & \tau_3 & \tau_1 & \tau_2\\ \hline
\utilde{\rho_3} & \rho_3 & \utilde{id} & \rho_2& \tau_2 & \tau_3 & \tau_1\\ \hline
\tau_1 & \tau_1 & \tau_2 & \tau_3 & id & \rho_2 & \rho_3\\ \hline
\tau_2 & \tau_2 & \tau_3 & \tau_1 & \rho_3 & id & \rho_2\\ \hline
\tau_3 & \tau_3 & \tau_1 & \tau_2 & \rho_2 & \rho_3 & id
\end{array}
$$
と同じになる場合もありますが
$${\rho_2\tau_1=\tau_3}$$(下線部)
$${\tau_1\rho_2=\tau_2}$$(波線部)
$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c|c|c|c}
& id & \utilde{\rho_2} & \rho_3 & \underline{\tau_1} & \tau_2 & \tau_3\\ \hline\hline
id & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3\\ \hline
\underline{\rho_2} & \rho_2 & \rho_3 & id & \underline{\tau_3} & \tau_1 & \tau_2\\ \hline
\rho_3 & \rho_3 & id & \rho_2& \tau_2 & \tau_3 & \tau_1\\ \hline
\utilde{\tau_1} & \tau_1 & \utilde{\tau_2} & \tau_3 & id & \rho_2 & \rho_3\\ \hline
\tau_2 & \tau_2 & \tau_3 & \tau_1 & \rho_3 & id & \rho_2\\ \hline
\tau_3 & \tau_3 & \tau_1 & \tau_2 & \rho_2 & \rho_3 & id
\end{array}
$$
や
$${\tau_1\tau_2=\rho_2}$$(下線部)
$${\tau_2\tau_1=\rho_3}$$(波線部)
$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c|c|c|c}
& id & \rho_2 & \rho_3 & \utilde{\tau_1} & \underline{\tau_2} & \tau_3\\ \hline\hline
id & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3\\ \hline
\rho_2 & \rho_2 & \rho_3 & id & \tau_3 & \tau_1 & \tau_2\\ \hline
\rho_3 & \rho_3 & id & \rho_2& \tau_2 & \tau_3 & \tau_1\\ \hline
\underline{\tau_1} & \tau_1 & \tau_2 & \tau_3 & id & \underline{\rho_2} & \rho_3\\ \hline
\utilde{\tau_2} & \tau_2 & \tau_3 & \tau_1 & \utilde{\rho_3} & id & \rho_2\\ \hline
\tau_3 & \tau_3 & \tau_1 & \tau_2 & \rho_2 & \rho_3 & id
\end{array}
$$
のように、積の順序を入れ替えると、一般には結果が異なります。
演算や操作の順序を入れ替えても結果が同じになるとき、『可換』であるといいます。例えば、実数のたし算やかけ算は可換です。
例 $${2+1=1+2}$$
$${3\times(-2)=(-2)\times3}$$
上記で示した通り、一般に置換の積は順序を入れ替えると結果が異なるので、可換ではありません。
以下、他のすべての部分群に関して、該当している部分について置換の積の演算表を記していきます。
$${A_3=\{id, \rho_2, \rho_3\}}$$ については
$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-11pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
& id & \rho_2 & \rho_3\\ \hline\hline
id & id & \rho_2 & \rho_3\\ \hline
\rho_2 & \rho_2 & \rho_3 & id\\ \hline
\rho_3 & \rho_3 & id & \rho_2
\end{array}
$$
得られる $${3\times3=9}$$ 通りの結果は、すべて $${A_3}$$ の要素になっているので、$${A_3}$$ は置換の積について閉じていることがわかります。
また、どの縦の1列をみても、どの横の1列をみても $${A_3}$$ の要素がすべて出そろっており、一般にこれは群であることの性質(の1つ)です。先ほどやった $${S_3}$$ の置換の積の演算表も、そのようになっていることに注目してください。
$${\{id, \tau_1\}}$$ については
$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
& id & \tau_1\\ \hline\hline
id & id & \tau_1\\ \hline
\tau_1 & \tau_1 & id
\end{array}
$$
得られる $${2\times2=4}$$ 通りの結果は、すべて $${\{id, \tau_1\}}$$ の要素になっているので、$${\{id, \tau_1\}}$$ は置換の積について閉じていることがわかります。
また、どの縦の1列をみても、どの横の1列をみても $${\{id, \tau_1\}}$$ の要素がすべて出そろっており、一般にこれは群であることの性質です。
以下、他の部分群について結果だけを記していきます。
$${\{id, \tau_2\}}$$ については
$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
& id & \tau_2\\ \hline\hline
id & id & \tau_2\\ \hline
\tau_2 & \tau_2 & id
\end{array}
$$
$${\{id, \tau_3\}}$$ については
$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
& id & \tau_3\\ \hline\hline
id & id & \tau_3\\ \hline
\tau_3 & \tau_3 & id
\end{array}
$$
$${\{id\}}$$ については
$$
\def\arraystretch{1.5}
\hspace{35pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c}
& id\\ \hline\hline
id & id
\end{array}
$$
部分群ではない場合の演算表
比較として、部分群ではないいくつかの集合について、置換の積の表を記していきます。
(例1)$${\{\tau_1, \tau_2, \tau_3\}}$$
$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-11pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
& \tau_1 & \tau_2 & \tau_3\\ \hline\hline
\tau_1 & id & \rho_2 & \rho_3\\ \hline
\tau_2 & \rho_3 & id & \rho_2\\ \hline
\tau_3 & \rho_2 & \rho_3 & id
\end{array}
$$
そもそも要素に単位元 $${id}$$ が含まれていないので(群の定義 (3) を満たしていないので)部分群ではありませんが、置換の積で得られる要素はすべて $${\{\tau_1, \tau_2, \tau_3\}}$$ の要素ではないので、群の定義 (1) も満たしておらず、部分群ではありません。
(例2)$${\{id, \tau_2, \tau_3\}}$$
$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-11pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
& id & \tau_2 & \tau_3\\ \hline\hline
id & id & \tau_2 & \tau_3\\ \hline
\tau_2 & \tau_2 & id & \underline{\rho_2}\\ \hline
\tau_3 & \tau_3 & \underline{\rho_3} & id
\end{array}
$$
$${\rho_2}$$ と $${\rho_3}$$ は $${\{id, \tau_2, \tau_3\}}$$ の要素ではないので(下線部)、群の定義 (1) を満たしておらず、部分群ではありません。
(例3)$${\{id, \rho_2\}}$$ については
$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
& id & \rho_2\\ \hline\hline
id & id & \rho_2\\ \hline
\rho_2 & \rho_2 & \underline{\rho_3}
\end{array}
$$
$${\rho_3}$$ は $${\{id, \rho_2\}}$$ の要素ではないので(下線部)、群の定義 (1) を満たしておらず、部分群ではありません。
ここで、新しい集合の概念、補集合について解説します。
補集合について
考えている対象全体の集合を全体集合といいます。全体集合 $${U}$$ とその部分集合 $${A}$$ が決まっているとき、$${A}$$ に属さない $${U}$$ の要素をすべて集めたものを、$${U}$$ に関する $${A}$$ の補集合といい、$${\overline{A}}$$ と表します。全体集合の中で $${A}$$ でない部分が $${A}$$ の補集合です。

一般に、$${A}$$ と $${\overline{A}}$$ の和集合(両方合わせた集合)は $${U}$$ であり、$${A}$$ と $${\overline{A}}$$ に共通部分(重なる部分)はありません。
例えば、$${U=\{1, 2, 3, 4, 5\}}$$ を全体集合、$${A=\{1, 2, 3\}}$$ を部分集合とすると、$${U}$$ に関する $${A}$$ の補集合は
$${\overline{A}=\{4, 5\}}$$

$${A}$$ と $${\overline{A}}$$ の和集合は $${U}$$ であり、$${A}$$ と $${\overline{A}}$$ に共通部分はありません。
また、$${U}$$ に関する $${B=\{2, 5\}}$$ の補集合は
$${\overline{B}=\{1, 3, 4\}}$$
となります。

$${B}$$ と $${\overline{B}}$$ の和集合は $${U}$$ であり、$${B}$$ と $${\overline{B}}$$ に共通部分はありません。
ここで後々のため、3次交代群 $${A_3}$$ を改めて
$${N=\{id, \rho_2, \rho_3\}}$$
と置き換えます。なぜ $${N}$$ という記号を使うのかは、後に判明します。すると、$${S_3}$$ に関する $${N}$$ の補集合 $${\overline{N}}$$ は、次の集合です。
$${\overline{N}=\{\tau_1, \tau_2, \tau_3\}}$$
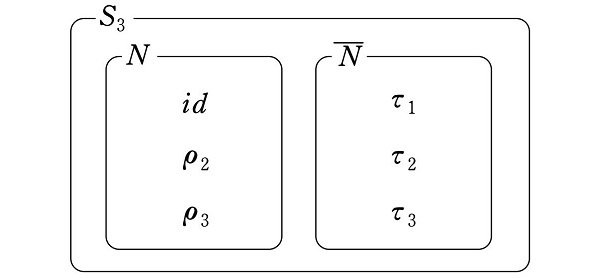
$${N}$$ と $${\overline{N}}$$ の和集合は $${S_3}$$ であり、$${N}$$ と $${\overline{N}}$$ に共通部分はありません。
なお、先に述べたように、$${N}$$ は $${S_3}$$ の部分群になりますが、$${\overline{N}}$$ は部分群ではありません。
ここで、$${N}$$ と $${\overline{N}}$$ の群構造における関連性をみていきます。ここから剰余類の解説です。
剰余類について
まず、$${N}$$ のすべての要素に
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
の要素を1つずつ順に作用させていきます。この作業により、$${N}$$ と $${\overline{N}}$$ の群構造における関連がみえてきます。
まず、$${id}$$ から作用させていきます。
(1a) 左から $${id}$$ を作用させる。
$${N=\{id, \rho_2, \rho_3\}}$$ の要素は $${id}$$, $${\rho_2}$$, $${\rho_3}$$ なので、この要素のすべてに、左から $${id}$$ を作用させると
$${idid=id}$$
$${id\rho_2=\rho_2}$$
$${id\rho_3=\rho_3}$$
これより、得られる結果はすべて $${N}$$ の要素です。
この $${N}$$ の要素のすべてに左から $${id}$$ を作用させた集合を
$${idN}$$
と表記し、次のように計算するとします。
$$
\begin{align*}
idN&=id\{id, \rho_2, \rho_3\}\\
&=\{idid, id\rho_2, id\rho_3\}\\
\end{align*}
$$
すべての $${N}$$ の要素に、$${id}$$ を左から分配していく要領です。それぞれの要素は置換の積になるので、それらを計算すると以下のようになります。
$$
\begin{align*}
idN&=id\{id, \rho_2, \rho_3\}\\
&=\{idid, id\rho_2, id\rho_3\}\\
&=\{id, \rho_2, \rho_3\}\\
&=N
\end{align*}
$$
結果は $${N}$$ 自身になります。
(1b) 右から $${id}$$ を作用させる。
$${N=\{id, \rho_2, \rho_3\}}$$ の要素のすべてに、右から $${id}$$ を作用させると
$${idid=id}$$
$${\rho_2id=\rho_2}$$
$${\rho_3id=\rho_3}$$
これも、得られる結果はすべて $${N}$$ の要素です。
この $${N}$$ の要素のすべてに右から $${id}$$ を作用させた集合を
$${Nid}$$
と表記し、次のように計算するとします。
$$
\begin{align*}
Nid&=\{id, \rho_2, \rho_3\}id\\
&=\{idid, \rho_2id, \rho_3id\}
\end{align*}
$$
すべての $${N}$$ の要素に、$${id}$$ を右から分配していく要領です。それぞれの要素は置換の積になるので、それらを計算すると以下のようになります。
$$
\begin{align*}
Nid&=\{id, \rho_2, \rho_3\}id\\
&=\{idid, \rho_2id, \rho_3id\}\\
&=\{id, \rho_2, \rho_3\}\\
&=N
\end{align*}
$$
これも、結果は $${N}$$ 自身になります。
(1a), (1b) をまとめると
$$
\begin{align*}
idN\hspace{-2pt}\underset{(1a)}{=}\hspace{-2pt}N\hspace{-2pt}\underset{(1b)}{=}\hspace{-2pt}Nid
\end{align*}
$$
となり、$${idN}$$ と $${Nid}$$ は $${N}$$ と同じ集合になります。
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|}\hline
idN=Nid=N & \hspace{31pt}\overline{N}\hspace{31pt}\\\hline\hline
id & \tau_1\\
\rho_2 & \tau_2\\
\rho_3 & \tau_3\\ \hline
\end{array}
$$
以下、$${S_3}$$ の他の要素について、(1a), (1b) と同じように計算していきます。
(2a) 左から $${\rho_2}$$ を作用させる。
$$
\begin{align*}
\rho_2N&=\rho_2\{id, \rho_2, \rho_3\}\\
&=\{\rho_2id, \rho_2\rho_2, \rho_2\rho_3\}\\
&=\{\rho_2, \rho_3, id\} \cdots (*1)\\
&=\{id, \rho_2, \rho_3\} \cdots (*2)\\
&=N
\end{align*}
$$
なお $${(*1)}$$ と $${(*2)}$$ は、集合として等しいことに注意してください。
$${\{\rho_2, \rho_3, id\}=\{id, \rho_2, \rho_3\}}$$
要素の並びは違っても、要素そのものは同じなので同じ集合となります。
(例)$${\{1, 2, 3\}}$$ と $${\{2, 3, 1\}}$$ は同じ集合なので
$${\{1, 2, 3\}=\{2, 3, 1\}}$$
(2b) 右から $${\rho_2}$$ を作用させる。
$$
\begin{align*}
N\rho_2&=\{id, \rho_2, \rho_3\}\rho_2\\
&=\{id\rho_2, \rho_2\rho_2, \rho_3\rho_2\}\\
&=\{\rho_2, \rho_3, id\}\\
&=\{id, \rho_2, \rho_3\}\\
&=N
\end{align*}
$$
(2a), (2b) をまとめると
$$
\begin{align*}
\rho_2N\hspace{-2pt}\underset{(2a)}{=}\hspace{-2pt}N\hspace{-2pt}\underset{(2b)}{=}\hspace{-2pt}N\rho_2
\end{align*}
$$
となり、$${\rho_2N}$$ と $${N\rho_2}$$ は $${N}$$ と同じ集合になります。
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|}\hline
\rho_2N=N\rho_2=N & \hspace{31pt}\overline{N}\hspace{31pt}\\\hline\hline
id & \tau_1\\
\rho_2 & \tau_2\\
\rho_3 & \tau_3\\ \hline
\end{array}
$$
(3a) 左から $${\rho_3}$$ を作用させる。
$$
\begin{align*}
\rho_3N&=\rho_3\{id, \rho_2, \rho_3\}\\
&=\{\rho_3id, \rho_3\rho_2, \rho_3\rho_3\}\\
&=\{\rho_3, id, \rho_2\}\\
&=\{id, \rho_2, \rho_3\}\\
&=N
\end{align*}
$$
(3b) 右から $${\rho_3}$$ を作用させる。
$$
\begin{align*}
N\rho_3&=\{id, \rho_2, \rho_3\}\rho_3\\
&=\{id\rho_3, \rho_2\rho_3, \rho_2\rho_3\}\\
&=\{\rho_3, id, \rho_2\}\\
&=\{id, \rho_2, \rho_3\}\\
&=N
\end{align*}
$$
(3a), (3b) をまとめると
$$
\begin{align*}
\rho_3N\hspace{-2pt}\underset{(3a)}{=}\hspace{-2pt}N\hspace{-2pt}\underset{(3b)}{=}\hspace{-2pt}N\rho_3
\end{align*}
$$
となり、$${\rho_3N}$$ と $${N\rho_3}$$ は $${N}$$ と同じ集合になります。
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|}\hline
\rho_3N=N\rho_3=N & \hspace{31pt}\overline{N}\hspace{31pt}\\\hline\hline
id & \tau_1\\
\rho_2 & \tau_2\\
\rho_3 & \tau_3\\ \hline
\end{array}
$$
(4a) 左から $${\tau_1}$$ を作用させる。
$$
\begin{align*}
\tau_1N&=\tau_1\{id, \rho_2, \rho_3\}\\
&=\{\tau_1id, \tau_1\rho_2, \tau_1\rho_3\}\\
&=\{\tau_1, \tau_2, \tau_3\}\\
&=\overline{N}
\end{align*}
$$
より、結果は $${N}$$ の補集合 $${\overline{N}}$$ となります。$${\overline{N}}$$ は「$${S_3}$$ に関する $${N}$$ に属さない要素全体の集合」であることは先に述べました。
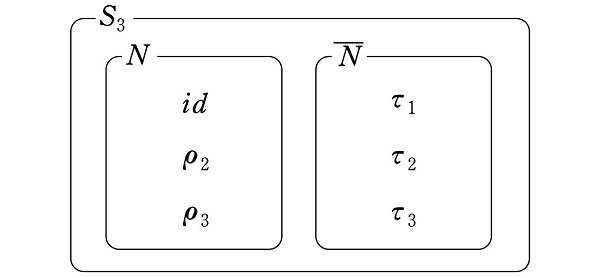
(4b) 右から $${\tau_1}$$ を作用させる。
$$
\begin{align*}
N\tau_1&=\{id, \rho_2, \rho_3\}\tau_1\\
&=\{id\tau_1, \rho_2\tau_1, \rho_3\tau_1\}\\
&=\{\tau_1, \tau_3, \tau_2\}\\
&=\{\tau_1, \tau_2, \tau_3\}\\
&=\overline{N}
\end{align*}
$$
(4a), (4b) をまとめると
$$
\begin{align*}
\tau_1N\hspace{-2pt}\underset{(4a)}{=}\hspace{-2pt}{\overline{N}}\hspace{-2pt}\underset{(4b)}{=}\hspace{-2pt}N\tau_1
\end{align*}
$$
となり、$${\tau_1N}$$ と $${N\tau_1}$$ は $${N}$$ の補集合 $${\overline{N}}$$ と同じ集合になります。先ほどまでは $${N}$$ でしたが、ここからは $${\overline{N}}$$ に変わります。
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|}\hline
\hspace{31pt}N\hspace{31pt} & \tau_1N=N\tau_1=\overline{N}\\\hline\hline
id & \tau_1\\
\rho_2 & \tau_2\\
\rho_3 & \tau_3\\ \hline
\end{array}
$$
(5a) 左から $${\tau_2}$$ を作用させる。
$$
\begin{align*}
\tau_2N&=\tau_2\{id, \rho_2, \rho_3\}\\
&=\{\tau_2id, \tau_2\rho_2, \tau_2\rho_3\}\\
&=\{\tau_2, \tau_3, \tau_1\}\\
&=\{\tau_1, \tau_2, \tau_3\}\\
&=\overline{N}
\end{align*}
$$
(5b) 右から $${\tau_2}$$ を作用させる。
$$
\begin{align*}
N\tau_2&=\{id, \rho_2, \rho_3\}\tau_2\\
&=\{id\tau_2, \rho_2\tau_2, \rho_3\tau_2\}\\
&=\{\tau_2, \tau_1, \tau_3\}\\
&=\{\tau_1, \tau_2, \tau_3\}\\
&=\overline{N}
\end{align*}
$$
(5a), (5b) をまとめると
$$
\begin{align*}
\tau_2N\hspace{-2pt}\underset{(5a)}{=}\hspace{-2pt}{\overline{N}}\hspace{-2pt}\underset{(5b)}{=}\hspace{-2pt}N\tau_2
\end{align*}
$$
となり、$${\tau_2N}$$ と $${N\tau_2}$$ は$${N}$$ の補集合 $${\overline{N}}$$ と同じ集合になります。
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|}\hline
\hspace{31pt}N\hspace{31pt} & \tau_2N=N\tau_2=\overline{N}\\\hline\hline
id & \tau_1\\
\rho_2 & \tau_2\\
\rho_3 & \tau_3\\ \hline
\end{array}
$$
(6a) 左から $${\tau_3}$$ を作用させる。
$$
\begin{align*}
\tau_3N&=\tau_3\{id, \rho_2, \rho_3\}\\
&=\{\tau_3id, \tau_3\rho_2, \tau_3\rho_3\}\\
&=\{\tau_3, \tau_1, \tau_2\}\\
&=\{\tau_1, \tau_2, \tau_3\}\\
&=\overline{N}
\end{align*}
$$
(6b) 右から $${\tau_3}$$ を作用させる。
$$
\begin{align*}
N\tau_3&=\{id, \rho_2, \rho_3\}\tau_3\\
&=\{id\tau_3, \rho_2\tau_3, \rho_3\tau_3\}\\
&=\{\tau_3, \tau_2, \tau_1\}\\
&=\{\tau_1, \tau_2, \tau_3\}\\
&=\overline{N}
\end{align*}
$$
(6a), (6b) をまとめると
$$
\begin{align*}
\tau_3N\hspace{-2pt}\underset{(6a)}{=}\hspace{-2pt}{\overline{N}}\hspace{-2pt}\underset{(6b)}{=}\hspace{-2pt}N\tau_3
\end{align*}
$$
となり、$${\tau_3N}$$ と $${N\tau_3}$$ は$${N}$$ の補集合 $${\overline{N}}$$ と同じ集合となります。
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|}\hline
\hspace{31pt}N\hspace{31pt} & \tau_3N=N\tau_3=\overline{N}\\\hline\hline
id & \tau_1\\
\rho_2 & \tau_2\\
\rho_3 & \tau_3\\ \hline
\end{array}
$$
以上の結果を列挙すると、次にようになります。
$$
\begin{alignat*}{3}
&(1a), (1b) より idN & &=Nid& &=N\\
&(2a), (2b) より \rho_2N & &=N\rho_2& &=N\\
&(3a), (3b) より \rho_3N & &=N\rho_3& &=N\\
&(4a), (4b) より \tau_1N & &=N\tau_1& &=\overline{N}\\
&(5a), (5b) より \tau_2N & &=N\tau_2& &=\overline{N}\\
&(6a), (6b) より \tau_3N & &=N\tau_3& &=\overline{N}
\end{alignat*}
$$
図にすると
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|}\hline
idN=Nid=N & \tau_1N=N\tau_1=\overline{N}\\
\rho_2N=N\rho_2=N & \tau_2N=N\tau_2=\overline{N}\\
\rho_3N=N\rho_3=N & \tau_3N=N\tau_3=\overline{N}\\\hline\hline
id & \tau_1\\
\rho_2 & \tau_2\\
\rho_3 & \tau_3\\ \hline
\end{array}
$$
このことから、次のような関係 (1)~(3) が見てとれます。
(1) 左剰余類による類別
これまで計算してきた
$$
\begin{align*}
idN, \rho_2N, \rho_3N, \tau_1N, \tau_2N, \tau_3N
\end{align*}
$$
のそれぞれを、$${N}$$ による『左剰余類』といいます。左から要素を作用させているので、”左”剰余類といいます。
すると、(1a), (2a), (3a) より、左剰余類のうち $${id, \rho_2, \rho_3}$$ を作用させた
$$
\begin{align*}
idN, \rho_2N, \rho_3N
\end{align*}
$$
は、すべて $${N=\{id, \rho_2, \rho_3\}}$$ と等しくなります。
$$
\begin{align*}
idN=\rho_2N=\rho_3N=N
\end{align*}
$$
一方、(4a), (5a), (6a) より、$${\tau_1, \tau_2, \tau_3}$$ を作用させた
$$
\begin{align*}
\tau_1N, \tau_2N, \tau_3N
\end{align*}
$$
は、すべて $${\overline{N}=\{\tau_1, \tau_2, \tau_3\}}$$ と等しくなります。
$$
\begin{align*}
\tau_1N=\tau_2N=\tau_3N=\overline{N}
\end{align*}
$$
これにより、群 $${S_3}$$ は左剰余類によって
$${idN=\rho_2N=\rho_3N=\{id, \rho_2, \rho_3\}}$$
のグループと
$${\tau_1N=\tau_2N=\tau_3N=\{\tau_1, \tau_2, \tau_3\}}$$
のグループの、要素が3個ずつの異なる2つのグループに分けることができます。
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|}\hline
idN=\rho_2N=\rho_3N & \tau_1N=\tau_2N=\tau_3N\\
のグループ & のグループ\\ \hline\hline
id & \tau_1\\
\rho_2 & \tau_2\\
\rho_3 & \tau_3\\ \hline
\end{array}
$$
このように、左剰余類によっていくつかの異なるグループに分けることを『左剰余類による類別』といいます(注1)。
<左剰余類による類別>

代表元について
なお、左剰余類の要素(元)を1つ選んで代表元とすることができます。
例えば $${idN}$$ グループにおいては、代表元として $${id, \rho_2, \rho_3}$$ の3通りの選び方があります。代表元とは、いわば各グループの「班長」のようなものです。同じ剰余類 $${idN}$$ でも
$${id}$$ を班長として選んだ場合は $${idN}$$
$${\rho_2}$$ を班長として選んだ場合は $${\rho_2N}$$
$${\rho_3}$$ を班長として選んだ場合は $${\rho_3N}$$
同じ剰余類 $${\tau_1N}$$ でも
$${\tau_1}$$ を班長として選んだ場合は $${\tau_1N}$$
$${\tau_2}$$ を班長として選んだ場合は $${\tau_2N}$$
$${\tau_3}$$ を班長として選んだ場合は $${\tau_3N}$$
と、代表元(班長)が左にくるように表記を変化させます。

$${idN, \rho_2N, \rho_3N}$$ はすべて同じ左剰余類、$${\tau_1N, \tau_2N, \tau_3N}$$ もすべて同じ左剰余類ですが、その作り方は異なるので、表記を変えて区別することが(後に正規部分群の考え方を導入する上で)重要となります。
(2) 右剰余類による類別
これまで計算してきた
$$
\begin{align*}
Nid, N\rho_2, N\rho_3, N\tau_1, N\tau_2, N\tau_3
\end{align*}
$$
のそれぞれを、$${N}$$ による『右剰余類』といいます。右から要素を作用させているので、”右”剰余類といいます。
すると、(1b), (2b), (3b) より、右剰余類のうち $${id, \rho_2, \rho_3}$$ を作用させた
$$
\begin{align*}
Nid, N\rho_2, N\rho_3
\end{align*}
$$
は、すべて $${N=\{id, \rho_2, \rho_3\}}$$ と等しくなります。
$$
\begin{align*}
Nid=N\rho_2=N\rho_3=N
\end{align*}
$$
一方、(4b), (5b), (6b) より、$${\tau_1, \tau_2, \tau_3}$$ を作用させた
$$
\begin{align*}
N\tau_1, N\tau_2, N\tau_3
\end{align*}
$$
は、すべて $${\overline{N}=\{\tau_1, \tau_2, \tau_3\}}$$ と等しくなります。
$$
\begin{align*}
N\tau_1=N\tau_2=N\tau_3=\overline{N}
\end{align*}
$$
これにより、群 $${S_3}$$ は右剰余類によって
$${Nid=N\rho_2=N\rho_3}$$
のグループと
$${N\tau_1=N\tau_2=N\tau_3}$$
のグループの、要素が3個ずつの異なる2つのグループに分けることができます。
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|}\hline
Nid=N\rho_2=N\rho_3 & N\tau_1=N\tau_2=N\tau_3\\
のグループ & のグループ\\ \hline\hline
id & \tau_1\\
\rho_2 & \tau_2\\
\rho_3 & \tau_3\\ \hline
\end{array}
$$
このように、右剰余類によっていくつかの異なるグループに分けることを『右剰余類による類別』といいます。
<右剰余類による類別>

右剰余類においても、要素(元)を1つ選んで代表元とすることができます。同じ右剰余類 $${Nid}$$ でも
$${id}$$ を班長として選んだ場合は $${Nid}$$
$${\rho_2}$$ を班長として選んだ場合は $${N\rho_2}$$
$${\rho_3}$$ を班長として選んだ場合は $${N\rho_3}$$
同じ右剰余類 $${N\tau_1}$$ でも
$${\tau_1}$$ を班長として選んだ場合は $${N\tau_1}$$
$${\tau_2}$$ を班長として選んだ場合は $${N\tau_2}$$
$${\tau_3}$$ を班長として選んだ場合は $${N\tau_3}$$
と、代表元(班長)が右にくるように表記を変化させます。
ここまでは左剰余類と右剰余類を個別にみてきましたが、次に左剰余類と右剰余類の関係性をみていきましょう。両者には次のような関係があります。
(3) 左剰余類による類別と右剰余類による類別は等しい
(1) より、$${S_3}$$ は左剰余類によって次の2つのグループに分けられました。
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|}\hline
idN=\rho_2N=\rho_3N & \tau_1N=\tau_2N=\tau_3N\\
のグループ & のグループ\\ \hline\hline
id & \tau_1\\
\rho_2 & \tau_2\\
\rho_3 & \tau_3\\ \hline
\end{array}
$$
また (2) より、$${S_3}$$ は右剰余類によって次の2つのグループに分けられました。
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|}\hline
Nid=N\rho_2=N\rho_3 & N\tau_1=N\tau_2=N\tau_3\\
のグループ & のグループ\\ \hline\hline
id & \tau_1\\
\rho_2 & \tau_2\\
\rho_3 & \tau_3\\ \hline
\end{array}
$$
ここで (1a) ~ (6b) より、$${S_3}$$ のそれぞれの要素について、左剰余類と右剰余類はすべて等しくなることが分かります。
$$
\hspace{-18pt}{\footnotesize \underset{\downarrow}{等しい}}\\
\\[-4pt]
\hspace{-18pt}\underset{\hspace{9pt}\downarrow}{{\footnotesize 左剰余類}}\hspace{-2pt}=\hspace{-2pt}\underset{\downarrow\hspace{8pt}}{{\footnotesize 右剰余類}}\\
\begin{rcases}
(1a), (1b) より idN=Nid\hspace{1pt}=\{id, \rho_2, \rho_3\}\\
(2a), (2b) より \rho_2N=N\rho_2=\{id, \rho_2, \rho_3\}\\
(3a), (3b) より \rho_3N=N\rho_3=\{id, \rho_2, \rho_3\}\\
\end{rcases}
(*3)
\\[5pt]
\begin{rcases}
(4a), (4b) より \tau_1N=N\tau_1=\,\{\tau_1, \tau_2, \tau_3\}\\
(5a), (5b) より \tau_2N=N\tau_2=\,\{\tau_1, \tau_2, \tau_3\}\\
(6a), (6b) より \tau_3N=N\tau_3=\,\{\tau_1, \tau_2, \tau_3\}\,
\end{rcases}
(*4)
$$
$${(*3)}$$ により、$${N=\{id, \rho_2, \rho_3\}}$$ と等しくなるグループで右剰余類と左剰余類の一致がみられ、$${(*4)}$$ により、$${\overline{N}=\{\tau_1, \tau_2, \tau_3\}}$$ と等しくなるグループで右剰余類と左剰余類の一致がみられます。
図にすると
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|}\hline
idN=\rho_2N=\rho_3N & \tau_1N=\tau_2N=\tau_3N\\
のグループ & のグループ\\ \hline\hline
id & \tau_1\\
\rho_2 & \tau_2\\
\rho_3 & \tau_3\\ \hline
\end{array}\\[5pt]
\hspace{64pt}\updownarrow {\small (*3) より等しい}\hspace{18pt}\updownarrow {\small (*4) より等しい}\\[5pt]
\def\arraystretch{1.5}
\begin{array}{|c|c|}\hline
Nid=N\rho_2=N\rho_3 & N\tau_1=N\tau_2=N\tau_3\\
のグループ & のグループ\\ \hline\hline
id & \tau_1\\
\rho_2 & \tau_2\\
\rho_3 & \tau_3\\ \hline
\end{array}
$$
以上のことから、「左剰余類による類別と右剰余類による類別は等しくなる」ことが分かります(下図)。
<左剰余類による類別>

$${\hspace{80pt}\Updownarrow}$$ 類別の方法は同じ
<右剰余類による類別>

左剰余類による「類別」と右剰余類による「類別」が等しくなる理由は、$${S_3}$$ のそれぞれの要素について、左剰余類と右剰余類が等しくなるからです。つまり、
$${idN=Nid}$$
$${\rho_2N=N\rho_2}$$
$${\rho_3N=N\rho_3}$$
$${\tau_1N=N\tau_1}$$
$${\tau_2N=N\tau_2}$$
$${\tau_3N=N\tau_3}$$
のすべてが成り立つからです。
この、左剰余類と右剰余類が等しくなる部分群
$${N=\{id, \rho_2, \rho_3\}}$$
のことを『正規部分群』といいます。$${N}$$ は Normal subgroup(正規部分群)の頭文字です。あらかじめ $${N}$$ と置いたのはそういう理由です。
正規部分群の定義を、大学の教科書にあるように正確に書くと次のようになります。
正規部分群の定義
$${N}$$ を群 $${G}$$ の部分群とする。$${G}$$ のすべての要素 $${g}$$ について
$$
\begin{align*}
gN=Ng
\end{align*}
$$
を満たすとき、$${N}$$ を $${G}$$ の『正規部分群』という。
***
$${gN=Ng}$$ とは、あくまでも集合として等しいことを意味します。つまり、$${G}$$ のすべての要素 $${g}$$ について、左剰余類 $${gN}$$(という集合)の要素と、右剰余類 $${Ng}$$(という集合)の要素が、同じになるということです。
$$
\begin{gather*}
\underset{左剰余類}{gN}\hspace{-5pt}=\hspace{-5pt}\underset{右剰余類}{Ng}\\[-3pt]
\hspace{1pt}\uparrow\\[-5pt]
\hspace{1pt}{\footnotesize 集合の要素が同じ}
\end{gather*}
$$
一般に、ある部分群が正規部分群のとき、その部分群による「左剰余類による類別」と「右剰余類による類別」は等しくなることが知られています。また逆に、ある部分群による「左剰余類による類別」と「右剰余類による類別」が等しいとき、その部分群は正規部分群であることも知られています(証明は割愛)。
$$
\begin{align*}
&正規部分群\\
\rightleftarrows &「左剰余類による類別」と「右剰余類による類別」\\
&は等しい \cdots (*5)
\end{align*}
$$
なお、左剰余類(という集合)と右剰余類(という集合)は、$${N}$$ が正規部分群であるとき一致するので、単に剰余類という場合は $${N}$$ が正規部分群である場合を指します。
(追記)
ガロアによれば、上記の $${(*5)}$$ を「正規部分群の定義」としているようです(参考『ガロア理論超入門』小林吹代著 他)。
正規部分群という言葉は当時はなかったため、ガロアは $${(*5)}$$ を満たすことを「固有の分解」と表現しています。この「固有の分解」をもたらすものが、今の言葉でいう正規部分群となります。
(追記終わり)
正規部分群の定義をイメージしやすくするために、正規部分群
$${N=\{id, \rho_2, \rho_3\}}$$
について、この定義を忠実に当てはめてみます。
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
のすべての要素
$${g=id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3}$$
について
$$
\begin{alignat*}{3}
&g=id & &のとき &idN&=Nid\\
&g=\rho_2 & &のとき &\rho_2N&=N\rho_2\\
&g=\rho_3 & &のとき &\rho_3N&=N\rho_3\\
&g=\tau_1 & &のとき &\tau_1N&=N\tau_1\\
&g=\tau_2 & &のとき &\tau_2N&=N\tau_2\\
&g=\tau_3 & &のとき &\tau_3N&=N\tau_3
\end{alignat*}
$$
のすべてが成り立つので、先ほどの正規部分群の定義より、$${N}$$ は $${S_3}$$ の正規部分群となることが分かります。
なお、部分群のすべてが正規部分群にはならないことを注意しておきます。群 $${S_3}$$ には以下の6通りの部分群がありました(本シリーズ(29))。
$${\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}=S_3}$$
$${\{id, \rho_2, \rho_3\}=A_3}$$
$${\{id, \tau_1\}}$$
$${\{id, \tau_2\}}$$
$${\{id, \tau_3\}}$$
$${\{id\}}$$
先ほど、$${\{id, \rho_2, \rho_3\}}$$ は正規部分群であることを示しました。
また、自分自身である $${S_3}$$ や、単位元だけからなる部分群 $${\{id\}}$$ も正規部分群となります(注2)。この自分自身や、要素が単位元だけからなる正規部分群を『自明な正規部分群』といいます。
正規部分群にならない例
次に、$${\{id, \tau_1\}}$$ が正規部分群となるかどうかをみていきます。
見やすさのため、$${M=\{id, \tau_1\}}$$ とおきましょう。$${N}$$ でやったときと同様の計算、つまり
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
のすべての要素
$${g=id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3}$$
を $${M}$$ に左右から作用させて、すべての要素に対して左剰余類と右剰余類が等しくなるかを確認していきます。つまり、すべての要素 $${g}$$ に対して
$$
\begin{align*}
gM=Mg
\end{align*}
$$
が成り立てば、$${M}$$ は正規部分群となります。
(1a) 左から $${id}$$ を作用させる。
$$
\begin{align*}
idM&=id\{id, \tau_1\}\\
&=\{idid, id\tau_1\}\\
&=\{id, \tau_1\}
\end{align*}
$$
(1b) 右から $${id}$$ を作用させる。
$$
\begin{align*}
Mid&=\{id, \tau_1\}id\\
&=\{idid, \tau_1id\}\\
&=\{id, \tau_1\}
\end{align*}
$$
(1a), (1b) より
$$
\begin{align*}
idM=Mid
\end{align*}
$$
となり、$${id}$$ については左剰余類と右剰余類が等しくなります。
$$
\def\arraystretch{1.5}
\begin{array}{|c|cc|}\hline
idM=Mid & \hspace{30pt} & \hspace{30pt}\\ \hline\hline
id & \rho_2 & \rho_3\\
\tau_1 & \tau_2 & \tau_2\\ \hline
\end{array}
$$
しかし
(2a) 左から $${\rho_2}$$ を作用させる。
$$
\begin{align*}
\rho_2M&=\rho_2\{id, \tau_1\}\\
&=\{\rho_2id, \rho_2\tau_1\}\\
&=\{\rho_2, \underline{\tau_3}\}
\end{align*}
$$
(2b) 右から $${\rho_2}$$ を作用させる。
$$
\begin{align*}
M\rho_2&=\{id, \tau_1\}\rho_2\\
&=\{id\rho_2, \tau_1\rho_2\}\\
&=\{\rho_2, \underline{\tau_2}\}
\end{align*}
$$
(2a), (2b) より、$${\tau_2}$$ と $${\tau_3}$$ が異なる要素となるので(下線部)
$$
\begin{align*}
\rho_2M\ne M\rho_2
\end{align*}
$$
図にすると
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|c|}\hline
idM=Mid & \hspace{18pt}\rho_2M\hspace{18pt} & \hspace{52pt}\\ \hline\hline
id & \rho_2 & \rho_3\\
\tau_1 & \tau_3 & \tau_2\\ \hline
\end{array}\\[2pt]
\hspace{122pt}\updownarrow {\small 左剰余類と右剰余類は異なる}\\[2pt]
\begin{array}{|c|c|c|}\hline
idM=Mid & \hspace{18pt}M\rho_2\hspace{18pt} & \hspace{52pt}\\ \hline\hline
id & \rho_2 & \rho_3\\
\tau_1 & \tau_2 & \tau_3\\ \hline
\end{array}
$$
1つでも成り立たないケースがあれば正規部分群ではないので、これで $${M=\{id, \tau_1\}}$$ は正規部分群ではないことが証明されました。
同様の理由で $${\{id, \tau_2\}}$$ と $${\{id, \tau_3\}}$$ も正規部分群とはならないので、以上をまとめると次のようになります。
$${\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$ (自明な)正規部分群である
$${\{id, \rho_2, \rho_3\}}$$ 正規部分群である
$${\{id, \tau_1\}}$$ 正規部分群ではない
$${\{id, \tau_2\}}$$ 正規部分群ではない
$${\{id, \tau_3\}}$$ 正規部分群ではない
$${\{id\}}$$ (自明な)正規部分群である
正規部分群でない場合の類別
ここで、先ほどの $${M=\{id, \tau_1\}}$$ について、左剰余類による類別と、右剰余類による類別がどのようになるのかを調べていきます。$${M}$$ が正規部分群ではないことはすでに証明されましたが、類別を調べるために、先ほどの計算をもう一度進めていきます。
まず、以下の (1a)~(2b) は本文ですでにやりました。
(1a) 左から $${id}$$ を作用させる。
$$
\begin{align*}
idM&=id\{id, \tau_1\}\\
&=\{idid, id\tau_1\}\\
&=\{id, \tau_1\}
\end{align*}
$$
(1b) 右から $${id}$$ を作用させる。
$$
\begin{align*}
Mid&=\{id, \tau_1\}id\\
&=\{idid, \tau_1id\}\\
&=\{id, \tau_1\}
\end{align*}
$$
(1a), (1b) より
$$
\begin{align*}
idM=Mid
\end{align*}
$$
(2a) 左から $${\rho_2}$$ を作用させる。
$$
\begin{align*}
\rho_2M&=\rho_2\{id, \tau_1\}\\
&=\{\rho_2id, \rho_2\tau_1\}\\
&=\{\rho_2, \underline{\tau_3}\}
\end{align*}
$$
(2b) 右から $${\rho_2}$$ を作用させる。
$$
\begin{align*}
M\rho_2&=\{id, \tau_1\}\rho_2\\
&=\{id\rho_2, \tau_1\rho_2\}\\
&=\{\rho_2, \underline{\tau_2}\}
\end{align*}
$$
(2a), (2b) より、$${\tau_2}$$ と $${\tau_3}$$ が異なる要素となるので(下線部)
$$
\begin{align*}
\rho_2M\ne M\rho_2
\end{align*}
$$
1つでも成り立たないケースがあれば正規部分群にはならないので、$${M}$$ は正規部分群にはなりません。ここまでは先ほどやりました。以下、$${S_3}$$ の残りの要素に対して、同様の計算を続けていきます。
(3a) 左から $${\rho_3}$$ を作用させる。
$$
\begin{align*}
\rho_3M&=\rho_3\{id, \tau_1\}\\
&=\{\rho_3id, \rho_3\tau_1\}\\
&=\{\rho_3, \tau_2\}
\end{align*}
$$
(3b) 右から $${\rho_3}$$ を作用させる。
$$
\begin{align*}
M\rho_3&=\{id, \tau_1\}\rho_3\\
&=\{id\rho_3, \tau_1\rho_3\}\\
&=\{\rho_3, \tau_3\}
\end{align*}
$$
(3a), (3b) より、$${\tau_2}$$ と $${\tau_3}$$ が異なる要素となるので
$$
\begin{align*}
\rho_3M\ne M\rho_3
\end{align*}
$$
(4a) 左から $${\tau_1}$$ を作用させる。
$$
\begin{align*}
\tau_1M&=\tau_1\{id, \tau_1\}\\
&=\{\tau_1id, \tau_1\tau_1\}\\
&=\{\tau_1, id\}\\
&=\{id, \tau_1\}
\end{align*}
$$
(4b) 右から $${\tau_1}$$ を作用させる。
$$
\begin{align*}
M\tau_1&=\{id, \tau_1\}\tau_1\\
&=\{id\tau_1, \tau_1\tau_1\}\\
&=\{\tau_1 id\}\\
&=\{id, \tau_1\}
\end{align*}
$$
(4a), (4b) より
$$
\begin{align*}
\rho_3M=M\rho_3
\end{align*}
$$
(5a) 左から $${\tau_2}$$ を作用させる。
$$
\begin{align*}
\tau_2M&=\tau_2\{id, \tau_1\}\\
&=\{\tau_2id, \tau_2\tau_1\}\\
&=\{\tau_2, \rho_3\}\\
&=\{\rho_3, \tau_2\}
\end{align*}
$$
(5b) 右から $${\tau_2}$$ を作用させる。
$$
\begin{align*}
M\tau_2&=\{id, \tau_1\}\tau_2\\
&=\{id\tau_2, \tau_1\tau_2\}\\
&=\{\tau_2, \rho_2\}\\
&=\{\rho_2, \tau_2\}
\end{align*}
$$
(5a), (5b) より、$${\rho_2}$$ と $${\rho_3}$$ が異なる要素となるので
$$
\begin{align*}
\tau_2M\ne M\tau_2
\end{align*}
$$
(6a) 左から $${\tau_3}$$ を作用させる。
$$
\begin{align*}
\tau_3M&=\tau_3\{id, \tau_1\}\\
&=\{\tau_3id, \tau_3\tau_1\}\\
&=\{\tau_3, \rho_2\}\\
&=\{\rho_2, \tau_3\}
\end{align*}
$$
(6b) 右から $${\tau_3}$$ を作用させる。
$$
\begin{align*}
M\tau_3&=\{id, \tau_1\}\tau_3\\
&=\{id\tau_3, \tau_1\tau_3\}\\
&=\{\tau_3, \rho_3\}\\
&=\{\rho_3, \tau_3\}
\end{align*}
$$
(6a), (6b) より、$${\rho_2}$$ と $${\rho_3}$$ が異なる要素となるので
$$
\begin{align*}
\tau_3M\ne M\tau_3
\end{align*}
$$
よって、部分群 $${M=\{id, \tau_1\}}$$ について
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
のすべての要素を左右から作用させると
$$
\begin{alignat*}{3}
&g=id & &のとき &idM&=Mid\\
&g=\rho_2 & &のとき &\rho_2M&\ne M\rho_2\\
&g=\rho_3 & &のとき &\rho_3M&\ne M\rho_3\\
&g=\tau_1 & &のとき &\tau_1M&=M\tau_1\\
&g=\tau_2 & &のとき &\tau_2M&\ne M\tau_2\\
&g=\tau_3 & &のとき &\tau_3M&\ne M\tau_3
\end{alignat*}
$$
次に、剰余類による類別について考察するため、これまでの結果を左剰余類、右剰余類ごとにまとめていきます。
左剰余類の結果を列挙すると
$$
\begin{align*}
(1a) より idM&=\{id, \tau_1\}\\
(2a) より \rho_2M&=\{\rho_2, \tau_3\}\\
(3a) より \rho_3M&=\{\rho_3, \tau_2\}\\
(4a) より \tau_1M&=\{id, \tau_1\}\\
(5a) より \tau_2M&=\{\rho_3, \tau_2\}\\
(6a) より \tau_3M&=\{\rho_2, \tau_3\}
\end{align*}
$$
となるので
$$
\begin{align*}
(1a), (4a) より idM&=\tau_1M=\{id, \tau_1\}\\
(2a), (6a) より \rho_2M&=\tau_3M=\{\rho_2, \tau_3\}\\
(3a), (5a) より \rho_3M&=\tau_2M=\{\rho_3, \tau_2\}
\end{align*}
$$
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|c|}\hline
idM=\tau_1M & \rho_2M=\tau_3M & \rho_3M=\tau_2M \\ \hline\hline
id & \rho_2 & \rho_3\\
\tau_1 & \tau_3 & \tau_2\\ \hline
\end{array}\\[2pt]
$$
よって、$${S_3}$$ は部分群 $${M=\{id, \tau_1\}}$$ による左剰余類によって、下図のように3つに類別されます。

一方、右剰余類の結果を列挙すると
$$
\begin{align*}
(1b) より Mid&=\{id, \tau_1\}\\
(2b) より M\rho_2&=\{\rho_2, \tau_2\}\\
(3b) より M\rho_3&=\{\rho_3, \tau_3\}\\
(4b) より M\tau_1&=\{id, \tau_1\}\\
(5b) より M\tau_2&=\{\rho_2, \tau_2\}\\
(6b) より M\tau_3&=\{\rho_3, \tau_3\}
\end{align*}
$$
となるので
$$
\begin{align*}
(1b), (4b) より Mid&=M\tau_1=\{id, \tau_1\}\\
(2b), (5b) より M\rho_2&=M\tau_2=\{\rho_2, \tau_2\}\\
(3b), (6b) より M\rho_3&=M\tau_3=\{\rho_3, \tau_3\}
\end{align*}
$$
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|c|}\hline
Mid=M\tau_1 & M\rho_2=M\tau_2 & M\rho_3=M\tau_3 \\ \hline\hline
id & \rho_2 & \rho_3\\
\tau_1 & \tau_2 & \tau_3\\ \hline
\end{array}\\[2pt]
$$
よって、$${S_3}$$ は部分群 $${M=\{id, \tau_1\}}$$ による右剰余類によって、下図のように3つに類別されます。

すると、正規部分群ではない部分群 $${M}$$ による右剰余類と左剰余類では、類別する方法が異なることが分かります(下図)。
<左剰余類による類別>

$${\hspace{98pt}\Updownarrow}$$ 類別の方法は異なる
<右剰余類による類別>

$${\rho_2M\ne M\rho_2}$$、$${\rho_3M\ne M\rho_3}$$ であることから、$${M=\{id, \tau_1\}}$$ は正規部分群ではありません。それにより、上図の様に左剰余類による類別と、右剰余類による類別は異なることが見てとれます。
一般に、正規部分群ではない部分群で類別する場合は、左剰余類で類別する場合と、右剰余類で類別する場合では、類別する方法は必ず異なります。
一方、正規部分群によって類別する場合は、左剰余類で類別する場合と、右剰余類で類別する場合では、類別する方法は必ず同じになります。先にやった正規部分群 $${N=\{id, \rho_2, \rho_3\}}$$ による類別がその例です。
(再掲)
<左剰余類による類別>

$${\hspace{156pt}\Updownarrow}$$ 類別の方法は同じ
<右剰余類による類別>

(まとめ)ガロアによる正規部分群の発見
ガロアは、ある方程式に解の公式が存在するかどうかを知りたい場合は、その方程式の解の入れ替えを表す群(対称群)を調べればよいことを発見しました。5次方程式の場合は5次対称群という群を調べることになります。 この対称群を調べるために、正規部分群とよばれる部分群を調べます。この正規部分群の重要性に初めて気付いたのがガロアです。

なぜ正規部分群なのか?、普通の部分群じゃダメなのか?、そのことついては次の章で詳しく解説していきます。
ここで概略だけを述べますと、正規部分群があれば、その正規部分群による左剰余類(または右剰余類)同士にある演算を定義することによって、その剰余類の集合に群構造を持たせることができます。剰余類は集合ですが、その集合そのものが1つの要素となって群(剰余群)となるわけです。
もう少し詳しく言うと、左剰余類にある演算を定義することによって、その演算に関して左剰余類の集合 $${\{idN, \tau_1N\}}$$ は群(剰余群)となり、

同様に、右剰余類にある演算を定義することによって、右剰余類の集合 $${\{Nid, N\tau_1\}}$$ も群(剰余群)となります。

さらにその剰余類の群は、回転運動とみなせる群(巡回群)であることが分かり、方程式側では「累乗根を加えること(添加)」と、群側では「回転を表す群(巡回群)」が1対1で対応します(ガロア対応)。これがいえるのは正規部分群のみであって、普通の部分群だとここまで成立しません。
つまり、群の構造が分かれば、その群構造によって、その方程式に解の公式が存在するかどうかが明確に分かるということです。
アーベルによるアイデアの概要は、本シリーズ (27) 他で述べています。アーベルは方程式の技巧的な式変形に、解の置換(入れ替え)をうまく用いて「5次以上の方程式には解の公式が存在しないこと」を証明しました。

しかしアーベルはその解の置換に、深遠なる構造までは見出せてはいませんでした。
そこにガロアが登場します。
解の置換に『群』という構造を初めて見いだし、解の公式が存在するかどうかは方程式をみるのではなく、群の構造をみればよいことをガロアは発見したのです。
詳しくは次の章で解説していきます。
(続く)
(コメント)
次の章で、正規部分群があれば、その正規部分群による右剰余類(または左剰余類)同士にある演算を定義することによって、剰余類の集合がその演算に関して群になることを解説していきます。ガロアの発見した重要テーマですが、これをかみ砕いて、なるべく専門的にならないように解説するのは非常に難しく、只今考慮中です(むしろ大学の教科書通りに書くのがカンタンに思えます)。
(注1)類別の身近な例
類別の身近な例として、奇数と偶数があります。理由は概略だけ記していきます。
整数の集合
$${\mathbb{Z}=\{\cdots, -3, -2, -1, 0, 1, 2, 3, \cdots\}}$$
は、たし算に関して群となります(本シリーズ (28))。その部分群として偶数の集合
$${\{\cdots, -4, -2, 0, 2, 4, \cdots\}}$$
を考えます。なお $${-4, -2}$$ のような負の偶数も含めて考えます。すると、その偶数の集合による右剰余類(または左剰余類)を考えることによって、整数の集合 $${\mathbb{Z}}$$ を、偶数の集合と奇数の集合に類別することができます。
これは $${2}$$ で割ったときの「余り」で類別しているとみることができます。例えば、 $${4}$$ は
$${4=2\times2+\underline{0}}$$
より余りは $${\underline{0}}$$、$${3}$$ は
$${3=2\times1+\underline{1}}$$
より余りは $${\underline{1}}$$ です。
負の整数の場合、例えば $${-4}$$ は
$${-4=2\times(-2)+\underline{0}}$$
より余りは $${\underline{0}}$$、$${-3}$$ は
$${-3=2\times(-2)+\underline{1}}$$
より余りは $${\underline{1}}$$ と考えます。これで、すべての整数に対して、余りが $${0}$$ になるグループ(偶数)と、$${1}$$ になるグループ(奇数)とで類別することができます。
余りのことを「剰余」(residue) というので、これが「剰余類」(residue class) という用語の由来です。
(注2)自明な正規部分群の証明
3次対称群
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
の自明な正規部分群として、自分自身 $${S_3}$$ と単位元のみからなる $${\{id\}}$$ があります。簡単ではありますが、これらが正規部分群であることを証明していきます。
復習として、正規部分群の定義は
<正規部分群の定義>
$${N}$$ を群 $${G}$$ の部分群とする。$${G}$$ のすべての要素 $${g}$$ について
$$
\begin{align*}
gN=Ng
\end{align*}
$$
を満たすとき、$${N}$$ を $${G}$$ の正規部分群という。
***
$${S_3}$$ に、 $${S_3}$$ の要素
$${g=id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3}$$
をそれぞれ左右から作用させて、すべての要素について
$$
\begin{align*}
gN=Ng
\end{align*}
$$
を満たすことを確認していきます。
(1a) $${id}$$ を左から作用させると
$$
\begin{align*}
idS_3&=id\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}\\
&=\{idid, id\rho_2, id\rho_3, id\tau_1, id\tau_2, id\tau_3\}\\
&=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}\\
&=S_3
\end{align*}
$$
(1b) $${id}$$ を右から作用させると
$$
\begin{align*}
S_3id&=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}id\\
&=\{idid, \rho_2id, \rho_3id, \tau_1id, \tau_2id, \tau_3id\}\\
&=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}\\
&=S_3
\end{align*}
$$
(1a), (1b) より
$$
\begin{align*}
idS_3=S_3id
\end{align*}
$$
(2a) $${\rho_2}$$ を左から作用させると
$$
\begin{align*}
\rho_2S_3&=\rho_2\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}\\
&=\{\rho_2id, \rho_2\rho_2, \rho_2\rho_3, \rho_2\tau_1, \rho_2\tau_2, \rho_2\tau_3\}\\
&=\{\rho_2, \rho_3, id, \tau_3, \tau_1, \tau_2\}\\
&=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}\\
&=S_3
\end{align*}
$$
(2b) $${\rho_2}$$ を右から作用させると
$$
\begin{align*}
S_3\rho_2&=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}\rho_2\\
&=\{id\rho_2, \rho_2\rho_2, \rho_3\rho_2, \tau_1\rho_2, \tau_2\rho_2, \tau_3\rho_2\}\\
&=\{\rho_2, \rho_3, id, \tau_2, \tau_3, \tau_1\}\\
&=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}\\
&=S_3
\end{align*}
$$
(2a), (2b) より
$$
\begin{align*}
\rho_2S_3=S_3\rho_2
\end{align*}
$$
以下、このように $${S_3}$$ のすべての要素について調べていけば、容易に
$$
\begin{align*}
\rho_3S_3&=S_3\rho_3\\
\tau_1S_3&=S_3\tau_1\\
\tau_2S_3&=S_3\tau_2\\
\tau_3S_3&=S_3\tau_3\\
\end{align*}
$$
は証明できるので、 $${S_3}$$ は正規部分群になります。
同様に $${\{id\}}$$ についても、$${S_3}$$ のすべての要素に対して、容易に
$$
\begin{align*}
id\{id\}&=\{id\}id\\
\rho_2\{id\}&=\{id\}\rho_2\\
\rho_3\{id\}&=\{id\}\rho_3\\
\tau_1\{id\}&=\{id\}\tau_1\\
\tau_2\{id\}&=\{id\}\tau_2\\
\tau_3\{id\}&=\{id\}\tau_3
\end{align*}
$$
は証明できるので、$${\{id\}}$$ は正規部分群になります。
(参考)各章の内容
(1)「2次方程式の解の公式」を式変形で導出
・平方完成
(2)「3次方程式の解の公式」を導出するための準備
・$${1}$$ の3乗根 $${\omega}$$
(3)「3次方程式の解の公式」を式変形で導出
・チルンハウス変換
(4)「解と係数の関係」と「対称式」の解説
(5)「対称式」を用いた「2次方程式の解の公式」の導出
(6)「解の置換」と「ラグランジュ・リゾルベント」の解説
(7)「ラグランジュ・リゾルベント」による「3次方程式の解の公式」の導出
(8)「遇置換」と「奇置換」の解説(ここから「アーベルの証明」の準備)
(9)「差積の2乗」が対称式となること、及び「差積」と平方根を結ぶ等式の証明。
(10)「平方根」「3乗根」と次々と累乗根を加えていくアイデア
(11)「アーベルの証明」のアイデアを用いて、なぜ「2次方程式の解の公式が存在するのか」を解説(添加する式について加筆予定)
(12)「アーベルの証明」のアイデアを用いて、なぜ「3次方程式の解の公式が存在するのか」を解説(前編)。「差積の2乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む(対称性の破壊)。
(13)「アーベルの証明」のアイデアを用いて、なぜ「3次方程式の解の公式が存在するのか」を解説(後編)。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む(対称性の破壊)。$${\longrightarrow}$$ 3次方程式の解の公式の完成
(14)「アーベルの証明」の解説①。5次方程式の解の差積(または差積の2乗の平方根)を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が5次置換(対称式)から遇置換シンメトリーへと破壊されることを解説。
(15)「アーベルの証明」の解説②。すべての置換は互換で表せることから、5次置換をすべて互換の積で表して、遇置換と奇置換に分類する。
(16)「アーベルの証明」の解説➂。「すべての遇置換は3次巡回置換の積で表される」ことの解説。
(17)「アーベルの証明」の解説➃(最後)。「任意の3次巡回置換が5次巡回置換の積で表せる」ことによって、5次方程式には解の公式が存在しないことが証明されることの解説。
(18)もっと分かりやすくシリーズ①「累乗根の添加」について重点解説。
(19)もっと分かりやすくシリーズ②「対称性の破壊」について重点解説。
(20)もっと分かりやすくシリーズ③「対称性を恒等置換まで破壊」することについて重点解説。
(21)もっと分かりやすくシリーズ➃ 何次方程式でも「最初に解の差積を添加して対称性を破壊すること」は常套手段。
(22)もっと分かりやすくシリーズ➄「解の和と差の連立」による2次方程式の解の公式の導出について。
(23)もっと分かりやすくシリーズ➅「対称式ではない解の公式を基本対称式で表す」ことのついて。
(24)もっと分かりやすくシリーズ➆「定数 $${\bm{\omega}}$$」について復習
(25)もっと分かりやすくシリーズ➇ 3次方程式の解の公式の導出方法「カルダノの方法」を復習
(26)もっと分かりやすくシリーズ➈「カルダノの方法」と「対称性の破壊」の関連について
(27)もっと分かりやすくシリーズ⑩ そもそもなぜ解の公式が存在しないかを『巡回置換』から紐解く
(28)中学でも分かるガロアの証明① ガロアの発見した「群」について簡単に解説
(29)中学でも分かるガロアの証明② ガロアの発見した「部分群」について簡単に解説
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
